渗透数学文化,创新情境命题
⦿江苏省启东中学 彭剑平
数学文化类试题是新高考数学试卷中命题的热点之一.数学文化是国家文化素质教育的重要组成部分,其内涵是在实践过程中不断探索形成的数学史、数学精神及其应用等.对数学文化的考查主要借助数学名著、数学故事以及数学名题等视角来创新设置,通过对数学文化的渗透,有效增强考生的理性思维与应用意识,培养爱国主义情怀.
1 数学名著
通过中国古代数学名著或世界数学名著等渗透数学文化,如我国古代的《数书九章》《张丘建算经》《孙子算经》等.
例1(2022年山东省潍坊市高考数学三模试卷)我国古代数学名著《九章算术》中给出了很多立体几何的结论,其中提到的多面体“鳖臑”是四个面都是直角三角形的三棱锥.若一个“鳖臑”的所有顶点都在球O的球面上,且该“鳖臑”的高为2,底面是腰长为2的等腰直角三角形.则球O的表面积为( ).
分析:根据题目条件,作出图形,设在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD且BC=CD=2,AB=2,证明出该三棱锥的四个面均为直角三角形,求出该三棱锥的外接球半径,结合球体表面积公式可得结果.
解析:如图1所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD且BC=CD=2,AB=2.
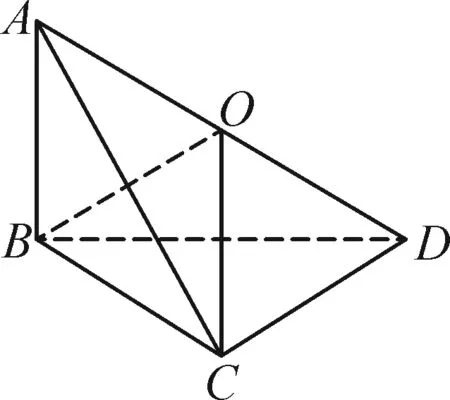
图1
因为AB⊥平面BCD,BC,BD,CD⊂平面BCD,所以AB⊥BC,AB⊥BD,CD⊥AB.
又CD⊥BC,AB∩BC=B,AB,BC⊂平面ABC,所以CD⊥平面ABC.
因为AC⊂平面ABC,所以AC⊥CD.


例2意大利数学家斐波那契的《算盘全书》中记载了一个有趣的问题:如果一对兔子每月能生1对小兔子(一雄一雌),不考虑其他因素,而每1对小兔子在它出生后的第三个月里,又能生1对小兔子.在特殊情况下,假定兔子都不发生死亡,那么由1对初生的小兔子开始,50个月后总共会有多少对兔子?
根据以上记载,从第1个月开始,以后每个月的兔子总对数依次为1,1,2,3,5,8,13,21,34,55,89,……,这个数列就是著名的“斐波那契数列”,它的递推公式是an=an-1+an-2(n≥3,n∈N*),其中a1=1,a2=1.若从该数列的前100项中随机抽取一个数,则这个数是偶数的概率为( ).
分析:根据斐波那契数列中项的分布规律以及递推公式加以归纳总结,确定每相邻3个数中有1个偶数,进而得到该数列的前100项中有33个偶数,利用古典概型的概率公式求解.

点评:涉及数学名著中的数学文化创新试题,关键是理解数学名著中对应创新情境的叙述与表达,综合题目所要求解的结论加以对比分析,构建相应的数学模型,利用相关的数学知识、思想方法来分析与解决相关的数学文化问题.
2 数学故事
通过数学家或数学故事渗透数学文化,如开普勒、毕达哥拉斯、斐波那契、希波克拉底、陈景润、黎曼等.

分析:根据题目条件,借助数学思想方法中的无限与有限的转化,通过无限根式的定值求解方法的应用与类比,转化为无限分式的定值求解,通过构建方程、解方程来确定无限分式的定值.
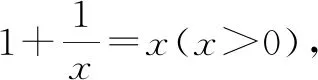
例4(湖南省三湘名校教育联盟2022届高三第二次大联考数学试卷·7)公元前5世纪,毕达哥拉斯学派利用顶角为36°的等腰三角形研究黄金分割,如图2,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于M,依此图形可求得cos 36°=( ).
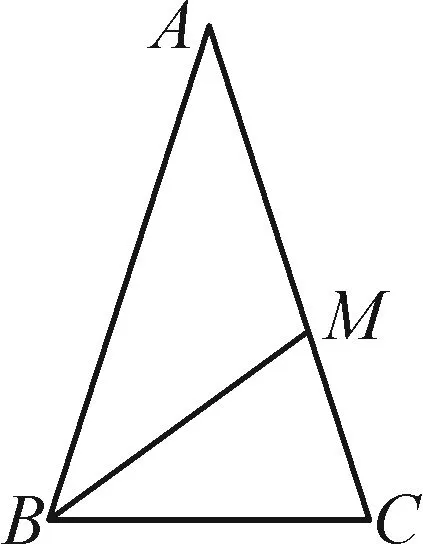
图2
分析:利用等腰三角形的性质、三角形边与角之间的关系、三角形相似的判定与性质、一元二次方程的解、正弦定理以及二倍角公式等的综合,合理转化,巧妙应用.
解析:由∠A=36°,可得∠ABC=∠ACB=72°.所以∠ACB=∠BMC=72°,∠MBC=∠MBA=∠A=36°.
设AB=x,BC=y=BM=AM.
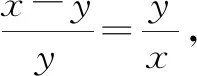
点评:涉及数学故事中的数学文化创新试题,关键是理解故事情境以及问题的设置情况,借助数学故事或问题表达中的思想方法、思路技巧等加以归纳、类比等推理与分析,结合数学运算、逻辑推理的综合应用,达到解决数学文化问题的目的.
3 数学名题
通过数学名题渗透数学文化,如勾股定理、阿波罗尼斯圆、哥德巴赫猜想、费马猜想或费马点等.
例5“哥德巴赫猜想”被誉为数学皇冠上的一颗明珠,是数学界尚未解决的三大难题之一,其内容是:“任意一个大于2的偶数都可以写成两个素数(质数)之和.”若我们将12拆成两个正整数的和,则拆成的和式中,在加数都大于3的条件下,两个加数均为素数的概率是( ).
分析:根据题目条件,在对12进行拆分时,罗列出所有加数都大于3以及两加数均为素数的拆分,进而利用古典概型的概率公式求解.
解析:将12拆成两个正整数的和,则拆成的和式中,加数都大于3的所有拆分为12=4+8,12=8+4,12=5+7,12=7+5,12=6+6,共计5个;而两个加数均为素数的拆分为12=7+5,12=5+7,共2个.

(1)若m=13,则使得an=1至少需要步雹程;
(2)若a9=1,则m所有可能取值的和为.
分析:根据创新定义,借助相应的步骤加以运算与推理,通过逐步计算即可求解.
解析:(1)若m=13,依题意,得3m+1=40→20→10→5→16→8→4→2→1,共需9个雹程.
(2)若a9=1,则a8=2,a7=4,a6=8或a6=1.
若a6=8,则

所以,a1的集合为{256,42,40,6,32,5,4},m的和为385.
故答案为:9;385.
点评:涉及数学名题中的数学文化创新试题,关键是理解此类数学名题的内容,掌握其内涵与实质,结合题目条件构建合理的数学模型,综合相关的数学知识、思想方法等进行解决.
合理关注一些古今中外的数学名著、数学故事以及数学名题等,巧妙融入相关的数学知识,通过对数学文化加以创新与渗透,提升考生的应用意识与创新意识等,进一步拓展视野,提升数学能力,养成优良品质.

