圆钢强化钢管混凝土梁正截面承载性能研究
刘德军,夏志恒,王军,左建平,常永全,昌佳
(1.中国矿业大学 煤炭资源与安全开采国家重点实验室,北京,100083;2.中国矿业大学(北京)力学与建筑工程学院,北京,100083;3.东南大学 土木工程学院,南京,211189;4.山东建筑大学 土木工程学院,山东 济南,250101)
众所周知,混凝土抗压性能优异,但抗弯能力弱,而钢管具有良好的弹塑性,但在受压时容易屈曲而丧失承载能力。在钢管中填充混凝土,可以防止钢管过早屈曲,使钢管刚度明显提高;同时,混凝土在钢管的约束下处于三向受压状态,抗压强度成倍提高。因此,钢管混凝土构件结合了混凝土和钢管的优点,两者协同作用,共同承受荷载,承载能力显著提高。作为一种新兴的组合结构,钢管混凝土构件主要用于承受轴心或小偏心荷载,被广泛应用于框架结构及桥梁工程中[1-3]。
近年来,学者对钢管混凝土构件的轴压性能进行了大量研究[4-11]。然而,由于各种原因,例如设计误差、制造误差、实际受力环境改变等,钢管混凝土构件不可避免地处于大偏心受压状态甚至纯弯状态。即使设计用于承受轴心荷载的钢管混凝土柱,在实际工程中也常会受到横向荷载而处于偏心受压状态,如风荷载和地震荷载等。因此,很多学者对钢管混凝土构件弯矩性能进行了大量研究,如HAN 等[12-20]通过试验、理论及数值模拟等方法系统探讨了钢管混凝土构件的弯曲性能。
当钢管混凝土构件截面内力处于弯矩主导状态时,往往因抗弯承载力不足而被破坏[21-22],因此,需要提高钢管混凝土构件的抗弯性能。由于碳纤维布有优异的抗拉性能、耐腐蚀且易于施工,常被用于钢管混凝土构件抗弯强化。CHEN等[23-29]通过试验分析了缠绕碳纤维布(包括全缠绕、U 型缠绕和部分缠绕)对钢管混凝土梁弯曲性能以及抗局部屈曲的影响规律,并结合数值模拟对其破坏模式进行了分析。此外,管内加筋也是提升钢管混凝土构件抗弯性能的一种常用方法。HADI等[30-33]提出管内加筋(双向对拉钢筋,内配格构式钢骨和碳纤维筋)以提高钢管混凝土梁抗弯性能,结合试验和数值模拟分析了管内加筋对试件的极限弯矩和抗弯刚度的提升效果。已有研究表明,纤维布缠绕加固是提升钢管混凝土构件弯曲性能的主要途径。但是在实际应用中,受限于使用环境,许多构件如应用于巷道支护的钢管混凝土支架难以缠绕加固[21-22]。
本文探讨在钢管拱腹焊接圆钢来提高钢管混凝土梁弯曲性能的有效性。首先,对在拱腹焊接不同直径圆钢的钢管混凝土梁进行四点弯曲试验。试验共选取6根直梁,其中1根未加固的梁作为参考梁,其他5根梁用不同直径的圆钢进行加固;然后,提出圆钢强化钢管混凝土梁(简称为强化梁)的正截面承载力计算理论,并通过试验验证其合理性,分析参考梁和圆钢强化梁中性轴偏移规律和各个部件对抗弯承载力的贡献。最后,采用建立的正截面承载力计算理论开展参数敏感性分析,研究混凝土抗压强度、钢管和圆钢的屈服强度、钢管径厚比对构件极限抗弯承载能力的影响。
1 试验研究
1.1 试件制作
首先截取6 根直径×管壁厚度为194×10 mm、长度为3 620 mm 的钢管,钢管两端磨平。然后采用边长为210 mm、厚度为10 mm 的方形钢块封堵直梁的一端,倾斜放置钢管,灌注C40混凝土并振捣密实,最后采用方形钢块封堵钢管另一端。试件浇筑完成后,放入标准养护实验室养护28 d。养护完成后,在强化钢管混凝土梁的腹拱处通长焊接圆钢。在6根钢管混凝土梁中,1根不焊接圆钢,用作参考梁,其余5 根分别焊接直径Φ为40,45,50,55 和60 mm 的圆钢。根据拱腹焊接圆钢的直径对试验试件进行编号,其中“S-40”试件表示拱腹通长焊接直径为40 mm 圆钢,其余依此类推;“S-0”为参考梁。从试验用钢管与圆钢上截取拉伸试样,经焊接高温处理后,参照“金属材料拉伸试验第1部分:室温实验方法”[34]测得钢管和圆钢的平均屈服强度均约为395 MPa。
1.2 试验过程
试样两端采用滚轴约束,允许试样绕平面内弯曲轴旋转。在量程为120 t的压力机上进行试验,液压千斤顶的集中荷载通过分配梁施加在试件的三分加载点上,三分点间的间距为940 mm,如图1所示。正式加载前,先对直梁试件进行三级预加载,加载荷载不超过预估承载力的10%,检查加载系统和测试仪表是否正常工作。正式加载时,采用静力单调连续分级加载。加载荷载达到预估承载力的60%之前,加载量级为40 kN/级;加载荷载达到预估承载力的60%~80%时,加载量级为20 kN/级;加载荷载超过预估承载力的80%后,加载量级减为10 kN/级。每级荷载的持续加载时间为1~2 min,待试件充分变形稳定后施加下一级荷载。待试件承载力不能继续提高时,停止加载。在整个试验过程中,实时测量跨中拱腹挠度变形。

图1 试件加载设计模型图Fig.1 Loading design model diagram of specimens
1.3 试验结果
1.3.1 破坏模式
当跨中挠度小于Le/30(即94 mm,Le为2 个支撑点之间的距离)时,随着挠度增加,弯矩显著增加。当跨中挠度大于Le/30时,随着挠度的继续增加,弯矩增加幅度明显降低,试样具有较高的延性。在整个试验过程中,试样没有发生旋转和平面外失稳。试验结束时,参考梁及强化梁的破坏模式都是整体弯曲破坏,见图2(强化梁的整体变形模式基本一致,本文仅以S-50 的变形模式作为示例)。观察试件的变形,钢管和底部圆钢未发现裂纹,钢管与圆钢之间的焊缝完整。由于钢管的径厚比(D/t)较大,钢管受压区未发生局部屈曲。

图2 试件变形破坏模式Fig.2 Deformation failure modes of specimens
1.3.2 极限弯矩
千斤顶的荷载为F,通过分配梁作用于三分点位置,三分点处集中荷载为F/2,Le=2 820 mm,则梁的跨中弯矩M的计算公式为
本试验所有试件最大竖向位移均大于Le/50(即56.4 mm)。因此,根据已有研究[35],取跨中竖向位移为Le/50 mm时对应的弯矩为极限弯矩Mu。另外,钟善桐[36]建议取钢管最大纤维应变达到10 000με为极限弯矩M′u。根据试验测得的数据,整理得到试件最大竖向位移dmax、最大竖向位移对应的跨中弯矩极值Mmax、极限弯矩Mu和M′u,如表1所示。用符号ζ表示强化梁相对于参考梁的弯矩提升比例,绘制强化梁相对于参考梁的弯矩提升曲线,如图3所示。
从表1 可以看出,钢管混凝土梁的跨中最大竖向位移均大于等于208 mm,达到了净跨距的Le/14,表明钢管混凝土梁具有良好的塑性,这与试验现象是一致的。焊接圆钢可以显著提升钢管混凝土梁的弯曲承载性能,且强化梁弯曲承载能力随着圆钢直径的增加而增大。从图3 可以看出,在本文所研究圆钢直径范围内,试件的抗弯承载能力随着圆钢横截面积增加整体呈线性提升趋势,其中跨中弯矩极值提升效果更明显。

表1 试件最大挠度、弯矩极值和极限弯矩Table 1 The maximum deflection,maximum value of bending moment and ultimate bending moment of specimens

图3 强化梁弯矩提升曲线Fig.3 Lifting curve of the bending moment of the reinforced beams
2 极限承载力计算
2.1 强化梁极限抗弯承载力
由于在钢管拱腹焊接圆钢,强化梁的初始中性轴向下偏移,处于圆形截面形心轴以下,且随着焊接圆钢直径增大,初始中性轴偏移量增大。假设试件达到极限弯矩时,强化梁的中性轴位置在距钢管截面形心轴y0处,见图4。建立正截面承载力计算方法,并假设如下:
1)在整个变形过程中,正截面始终保持为水平截面;
2)忽略混凝土的拉应力;
3)钢管的应力-应变关系采用二折线模型[37];
4)考虑钢管对混凝土的约束作用,混凝土的应力-应变关系采用Hu模型[38];
将极限弯矩对应的中性轴设为X轴,截面的轴向对称轴设为Y轴。假设钢管顶点到中性轴的距离为y1,则钢管截面形心至中性轴的距离y0=y1-R(R为钢管外半径)。钢管屈服点到中性轴X轴的距离y2可由下式确定:
式中:εy为钢管屈服时对应的应变;εcc为混凝土压溃时对应的应变;t为钢管的壁厚。
钢管弹性阶段的应力fs与屈服应力fy的关系可由下式确定:
式中:y为应力fs对应的截面高度到中性轴的距离。
受压区的压力分为两个部分:一部分为混凝土承受的压力Fc1,另一部分为钢管承受的压力Fc2,如图4所示。受拉区的拉力也可以分为两个部分,即钢管所承受的拉力Ft1和圆钢承受的拉力Ft2。

图4 圆钢强化梁正截面应变、应力分布Fig.4 Strain and stress distribution of the normal section of round steel reinforced beam
式中:σc为受压区混凝土对应的压应力;r为钢管的内半径;re为圆钢半径。
由于正截面处于纯弯受力状态,根据零轴力条件可得:
对中性轴取矩,可得强化梁的极限弯矩Mu0:
2.2 合理性验证
提取计算得到的极限弯矩Mu0,并将其与Mu和M′u进行对比,见表2。
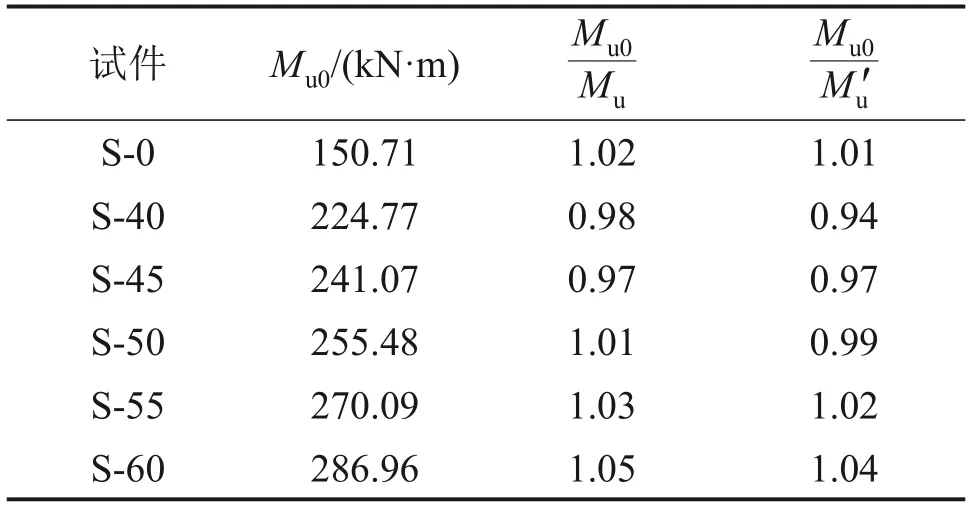
表2 试验和理论极限弯矩对比Table 2 Comparison of test results and calculation results of the ultimate bending moment
从表2可以看出,极限弯矩计算值与试验值吻合较好,表明建立的强化梁正截面承载性能计算理论是合理的,可以较好地预测钢管混凝土构件的极限抗弯承载力。
2.3 抗弯承载力提升机理分析
采用建立的正截面极限承载力计算理论计算试件中性轴位置,并提取正截面各个部分承担的弯矩,将其绘制成曲线,见图5。
分析结果表明,强化梁的中性轴位置明显下移,且圆钢直径越大,中性轴偏移量越大,总体呈现出线性变化规律(见图5(a))。这是由于跨中截面处于纯弯曲状态,截面没有轴向力,当其达到极限弯矩时,参考梁(即圆钢直径为0 mm时的钢管混凝土梁)由于受拉区混凝土的开裂,为满足截面零轴力的条件,中性轴需要往圆形截面形心轴上方偏移来补偿受拉区拉应力的损失。对于拱腹焊接圆钢的强化梁,由于焊接圆钢极大地增加了截面承受拉应力的能力,因此,与参考梁相比,中性轴需要往下偏移来满足截面零轴力的要求。对于参考梁,钢管承担绝大部分弯矩,管内混凝土承担的弯矩较小(图5(b))。对于强化梁,由于焊接圆钢降低了中性轴位置,提高受压区钢管承担弯矩的同时也减小受拉区钢管承担的弯矩,因此,钢管整体承担的弯矩(即受压区和受拉区钢管弯矩之和)基本保持不变(见图5(b)合图5(c))。圆钢和管内混凝土承担弯矩均随着圆钢直径的增加而增加,但是圆钢承担的弯矩增加速率明显高于管内混凝土承担的弯矩增加速率(图5(b))。因此,圆钢对于钢管混凝土梁抗弯承载能力的提升得益于两部分:一部分为圆钢本身的弯矩承载能力,另一部分是强化钢管混凝土梁正截面的中性轴下移,使得管内处于受压状态的混凝土面积增加,有效激发了管内混凝土的抗弯承载性能。需要指出的是,强化梁抗弯承载性能的提高主要得益于圆钢本身的抗弯承载性能。

图5 中性轴位置及试件各部分弯矩随圆钢直径的变化Fig.5 Position of the neutral axis and changes of the bending moment of each part of specimens with diameter of round steel
3 参数敏感性分析
本文第2节只考虑了焊接圆钢直径对试件抗弯承载能力的影响,下面采用建立的弯曲承载能力计算理论分析不同参数对圆钢强化梁极限抗弯承载能力的影响。研究参数包括混凝土的抗压强度、钢管和圆钢的屈服强度、钢管的径厚比(D/t)。设计参数和相应的结果见表3。
参数研究中所有试件钢管的外径为194 mm,圆钢的直径为50 mm。从表3可以看出,混凝土的抗压强度从20 MPa增大到60 MPa,试件的极限弯矩只提升了31.18 kN·m,提升幅度较小,约为13%,且达到极限弯矩时,中性轴的位置随着混凝土抗压强度的增加逐渐升高,受压区混凝土的面积随着混凝土强度的增大而减小。

表3 不同参数下试件极限弯矩和中性轴位置对比Table 3 Comparison of ultimate bending moment and neutral axis position of the specimens with different parameters
对屈服强度分别为245,320,395,470 和545 MPa 的圆钢和钢管进行参数分析,结果表明,试件的极限弯矩随着屈服强度的增大显著增加。此外,当钢管屈服强度从245 MPa提高到545 MPa时,试件的极限弯矩提升了101.21 kN·m,提升幅度约为49%。当圆钢屈服强度从245 MPa 提高到545 MPa 时,试件的极限弯矩提高了71.07 kN·m,提升幅度约为33%。但圆钢的横截面积是钢管横截面积的0.34 倍,说明提高圆钢屈服强度能更有效地提升强化梁的抗弯承载性能。这与2.3节的分析结论是一致的,即强化钢管混凝土梁抗弯承载性能的提高主要得益于圆钢本身的抗弯承载性能。这是由于当试件达到极限弯矩时,中性轴处于钢管截面内,整个圆钢截面都已进入屈服状态,且圆钢承担应力对中性轴取矩较大。
当钢管的壁厚分别为6,8,10,12 和14 mm时,D/t范围为13.9~33.3。从表3 可以看出,试件的极限弯矩和受压区混凝土的面积随着壁厚的增加而增大,但极限弯矩增加的幅度逐渐减小,说明对于圆钢强化梁来说,并非钢管壁厚越大,极限弯矩的提升效果越高。这是由于焊接圆钢降低了中性轴的位置,减小了受拉区钢管的截面面积,因此,随着钢管壁厚的增加,弯矩提升效果逐渐降低。
4 结论
1)腹拱焊接圆钢可以显著提高钢管混凝土梁的抗弯承载性能,且抗弯承载力随着圆钢直径增加而增大。
2)提出了圆钢强化钢管混凝土梁极限抗弯承载力的计算公式,该公式可以较好地预测钢管混凝土构件的极限抗弯承载力。
3)焊接圆钢可以降低钢管混凝土梁正截面中性轴位置,增大受压区混凝土的面积;随着焊接圆钢直径的增大,钢管承担的弯矩基本保持不变,圆钢和管内混凝土承载的弯矩提高,但圆钢承担弯矩的提高速率更快。因此,圆钢强化钢管混凝土梁抗弯承载性能的提高主要得益于圆钢的抗弯承载性能。
4)增加混凝土抗压强度对于圆钢强化梁极限弯矩的提升贡献不明显。随着钢管壁厚的增加,极限承载弯矩逐渐提高,但提高幅度逐渐降低。圆钢强化梁极限弯矩随着圆钢和钢管屈服强度增加而显著增大,且提高圆钢屈服强度对极限弯矩的提升效果更明显。

