数学建模活动的教学实践与思考

刘飞飞

摘  要：以“‘诱人的优惠券”为例，从学生的生活世界出发，以数学建模为载体，结合信息技术，培养学生从不同角度发现问题、提出问题、分析问题和解决问题的能力，全面提升学生的数学核心素养.

关键词：生活实际；数学建模；信息技术

一、研究背景

《普通高中数学课程标准（2017年版2020年修订）》指出，数学教育承载着落实立德树人根本任务、发展素质教育的功能；要提升学生的数学素养，引导学生会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界；突出数学主线，凸显数学的内在逻辑和思想方法；精选课程内容，处理好数学学科核心素养与知识技能之间的关系，强调数学与生活及其他学科的联系，提升学生应用数学解决实际问题的能力.

数学核心素养的表现是综合性的，数学的视野、态度、思维、价值判断与问题的解决交织在一起，这种综合的素养要求数学课程更具开放性，即不仅要在数学的圈子里看数学，更要通过数学去看世界. 这就需要教师具有跨学科思维素养，重视不同学科知识的交叉、融合，能够从学生的生活世界出发，设计相应的跨学科课程，加强知识之间的联系，培养学生从不同角度分析问题和解决问题的能力，实现由“知识传授”向“学科育人”教育目标的转变.

数学之所以具有廣泛的应用性，是因为它可以为其他学科知识的学习，以及生产实践和日常生活提供多样化的数学模型；数学建模活动问题层出不穷，活动方法丰富多彩，可以为学生提供多样化的、开放的探索活动空间，提升学生的跨学科意识，更好地培养学生发散性思维，引导学生从不同角度发现问题，提升学生综合运用多学科知识解决问题的能力.

二、研究内容

本文研究的内容是沪教版《普通高中教科书·数学》必修第四册第1部分“数学建模活动案例”中的“‘诱人的优惠券”. 这个主题与学生的生活密切相关，大家都曾因优惠券或多或少买过一些用处不大的东西，为此浪费了许多的时间和金钱，这些经历能够极大地激发学生的探究兴趣. 本案例主要的研究目的是通过完整的数学建模活动，加深学生对相关数学知识和技能的理解，并增强学生利用信息技术与数学知识的融合解决实际问题的能力.

三、课前准备

提前两周和学生确定主题，学生结合经验交流、思考，提出其认为合理的问题、设想和建议，并以小组合作的方式，通过搜集信息、实地调查尝试建模，同时结合信息技术，综合应用数学公式、图象、图表等表达形式，求解模型并检验结果.

四、研究过程

1. 实际情境

近年来，“双十一”逐渐演变成一年一度的购物狂欢节. 面对商家复杂的优惠规则，消费者都尝试用足优惠. 最近，某商家推出三种优惠券，分别是满199元减20元、满299元减50元、满499元减110元. 这些优惠券不可以叠加使用，但是它们可以与满400元减50元的购物津贴同时使用. 此外，这两类优惠方式有使用顺序，必须先使用商家的优惠券，再使用购物津贴.

2. 提出问题

组1：我们组倾向于理性消费，一次性消费一般不会达到400元，所以我们只考虑了满199元减20元和满299元减50元两种优惠方式.

组2：我们组考虑使用三种优惠券，探究是否购物金额越大享受的优惠越大.

组3：我们组考虑使用三种优惠券，再加上购物津贴，探究是否购物金额越大享受的优惠越大.

组4：我们组最关心的是如何用最少的钱买最多的东西.

组5：我们组从商家的角度考虑问题，探究如何设计优惠券才能使利润最大化.

3. 建立模型

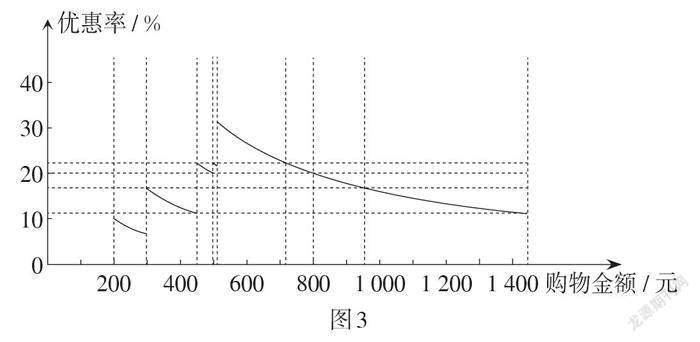
组1：对于满199元减20元和满299元减50元的优惠券，我们首先考虑的是购买商品的总金额是否满足优惠券的额度，然后比较其对应的优惠率，也就是将购物金额看作自变量[x，] 将优惠率看作函数值[y，] 则优惠率等于优惠的金额除以购物金额. 由此可以建立函数模型[y=0 0

组2：基于事先的考虑，我们组分别计算了在不同购物金额下对应使用三种优惠券的优惠率，具体数据如表1所示.

组3：我们组考虑了三种优惠券，再加上购物津贴. 相比于组2，考虑得更加周全. 因为当购物金额满400元时可以使用减50元的购物津贴，但是要先使用优惠券之后才能用购物津贴，所以满450元就可以同时使用满299元减50元的购物券和满400元减50元的购物津贴. 同理，满510元，可以使用满499元减110元的优惠券和满400元减50元的购物津贴. 由此可以建立分段函数模型

组4：我们最关心的是如何用最少的钱买最多的东西. 首先，当然要货比三家选择售价最低的商家；其次，我们发现有的商品还有打折的优惠，所以我们考虑的问题是“先打折再满减”和“先满减再打折”两种促销方式相比较，哪种方式更省钱. 为了简化模型，我们以买的所有商品都打五折为例进行建模.

（1）先打折再满减.

设原购物金额为[x]元，实际购物金额为[t]元，折扣率为[y，] 则折扣率等于实际购物金额除以原购物金额，即[y=tx.]

组5：我们实地调查各大商场，发现促销的方式有很多，如直接打折、满减、买二送一、积分返现等. 假设商场只考虑打折和满减这两种促销方式（两种促销方式不叠加），我们想比较哪一种促销方式商场获得的利润最大. 为了简化模型，假设商场商品以打八折或满100元减20元这两种方式进行促销. 设商品标价为[x]元，两种促销方式下消费金额对应的函数分别为[fx，gx].

可以看出，优惠率随着购物金额呈现循环往复的规律波动，在[199≤x<299，299≤x<499，x≥499]三个函数区间内，优惠率随着购物金额的增加而下降，在每个函数区间内，分别当[x=199，x=299，x=499]时，优惠率达到最大，分别约为10.1%，16.7%，22.0%，且这三个最大值也逐渐增大. 所以并不是购物金额越大，优惠率越高，而要在购物金额接近199元，299元，499元时考虑适当“凑单”，以便享受更大优惠. 其他情形还要理性消费，不要为了“凑单”而买一些无用的东西.

组3：如图3，用GeoGebra软件作图，可以看出当[0

组4：如图4，虚线代表“先打折，再满减”的情况；实线代表“先满减，再打折”的情况. 当[0

组5：分析对于满100元减20元的优惠模型g（x）=MOD（x，100）+INT（x/100）×（100-20）.]

例如，当[x=80]时，[fx=64，gx=80，f80

当[x=100]时，[fx=80，gx=80，f100=g100;]

当[x=150]时，[fx=120，gx=130，f150

当[x=200]时，[fx=160，gx=160，f200=g200.]

发现对于整百元的商品，两种促销方式价格一样，其余情况均为满减的方式对商家更有优势. 我们还利用伪代码编程仿真实现了自动化分析，编程如5所示.

我们可以用计算机编程，对变量进行赋值，通过比较选择最有利于商家的一种促销模式.

5. 回归现实，反思结果

各组分别从不同角度进行建模，并对所建模型进行分析. 其中，为了简化模型，我们只考虑了购物金额、优惠率或折扣率，但对现实仍然具有一定的指导意义. 例如，作为消费者，不要被商家的促销策略所诱导，我们已经知道并不是购物金额越大，优惠率就越高. 相反，随着购物金额的逐渐增大，优惠率还可能越来越低. 有时商场对不同商品采取的促销方式也不一样，如有的商品是直接打折，有的商品是满减，或者满额返券，这种促销方式可能更为复杂，因为返的券还要进行消费，往往要结合几种不同的优惠方式才能得到更多的优惠.

而作为商家，本次建模主要考虑的是先打折再满减和先满减再打折这两种促销方式哪种获利最多，实际上还有很多因素需要考虑，如消费者的心理、消费群体的特征，商场哪些商品适合打折、哪些商品适合满减等，除此之外还要考虑库存、成本、定价等因素. 有兴趣的同学可以在课后继续研究.

五、几点体会

本次数学建模活动，我们面对的是现实生活中购物消费的情境，各组学生从不同的角度提出问题，运用分类讨论的思想，把不同问题用分段函数加以表征，给出了简化的模型. 在求解模型时，利用Excel绘制散点图、折线图等，利用GeoGebra软件绘制函数图象，以及利用计算机编程，通过分析、比较与计算，得到了相应的结论.

数学建模问题一般比较复杂，需要进行长期的探索、研究，学生开始会觉得无从下手，甚至限于知识储备，可能会对数学建模活动望而生畏，这时需要教师及时指导，鼓励学生勇于参加数学建模活动，大胆提出问题，尝试建立数学模型. 数学建模活动需要团队合作，每位成员都要增强团队意识，充分发挥自己的特长，并善于吸纳队友的建议，通过集体的智慧，借助信息技术，使问题不断得以修正和解决.

数学建模与其他数学核心素养紧密相关：对现实问题进行数学表达需要学生具备数学抽象和逻辑推理素养；建立模型需要对数据、信息、图表等进行处理，需要学生具备直观想象素养；求解模型需要学生具备逻辑推理和数学运算素养. 而对模型的分析、修正等，不仅需要数学知识，更需要其他领域知识的辅助. 因此，数学建模活动是跨学科学习的良好载体，教师要不断增强跨学科意识，不断提高学生信息技术水平，增强学生对数学建模活动的情感体验，提高对数学建模的学习兴趣.

参考文献：

［1］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［2］黄翔，童莉，史宁中. 谈数学课程与教学中的跨学科思维［J］. 课程·教材·教法，2021，41（7）：106-111.

［3］王建忠，张萍. 基于计算思维的折扣分析［J］. 宜宾学院学报，2013，13（6）：29-32，42.