基于ADRC的无人直升机飞行控制系统设计

卢艳军，刘宏斌，张晓东

（沈阳航空航天大学自动化学院，沈阳 110136）

0 引言

无人驾驶飞行器是一种通过无线电远程控制和自带程序控制的飞行器，它可以完全或间断地通过车载电脑进行自动操作。无人直升机作为无人驾驶飞行器的一种，在无人驾驶飞行器大家庭中占有至关重要的地位，在某些特殊领域中极具优势。与旋翼机相比，无人直升机具有高续航、高载荷的优点[1]。与固定翼飞机相比，它具有高机动性、强侦查性的优点，可以定点悬停，低空飞行，探测周围环境。与载人直升机相比，它具有高能源效率、高安全性、高适应性、低成本等优点，可以在更为复杂的城市环境中得到广泛应用，如搜索、救援、消防、监视、电影行业的空中特技等。还可以代替飞行员执行更加危险的任务，有效减小甚至避免意外情况的发生[2]。在军事领域中，无人直升机对于战场上的情报勘察、物资支援、以及低空打击等方面都可以起到关键性的作用。军用无人直升机不但可以在战场上发挥巨大的作用，还是一个国家军事力量和综合国力的体现。在民事领域中，无人直升机在森林防火、抗震救灾、物流运输等方面具有不可或缺的作用[3]。正因如此，对无人直升机开展深度研究/研发工作尤为关键。无人直升机控制系统的设计是无人直升机的关键技术，然而，无人直升机作为高度耦合（坐标系间耦合、各部件间耦合）、非线性的高复杂度被控对象，其控制系统的设计尤其困难[4]。在我国科研人员的不懈攻关与大力研究下，我国在无人直升机控制技术的研发上已经有了长足的发展[5-6]。目前，国内外学者对无人直升机飞行控制系统的研究主要聚焦于如何有效降低由高耦合性和非线性带来的影响，进而降低误差，增强无人直升机的稳定性[7]，而飞行控制系统的准确性取决于其参数的设置与调整。因此，本文希望解决无人直升机飞行控制系统中的参数难以调整的问题，以期提高控制系统的精确度，使无人直升机的控制系统更加稳定。对无人直升机飞行控制系统的研究具有重大意义。

1 无人直升机飞行动力学模型

本文研究对象为常规带有尾桨的单旋翼跷跷板式结构的无人直升机[8]，具有普遍性。其机体结构主要由主旋翼、尾桨、机身、平尾、垂尾、自动倾斜器和起落架组成。

以无人直升机为研究对象，建立地面坐标系和机体坐标系，两种坐标系之间的关系如图1 所示。机体坐标系和地面坐标系各轴线之间的角度叫做姿态角，又称欧拉角。其中，OBXB与OEXEYE平面之间的夹角为俯仰角θ，以飞机抬头为正；OBXB与OEXE之间的夹角为偏航角ψ，以机头右偏为正；OBZB与OEZE轴的铅锤平面间的夹角为滚转角φ，以直升机向右倾斜为正。滚转角速度p、俯仰角速度q、偏航角速度r分别为角速度投影在机体坐标系OBXB、OBYB、OBZB轴上的分量。u、v、w分别为直升机在OBXB、OBYB、OBZB轴上的轴向速度。L、M、N分别为三轴力矩，即滚转力矩、俯仰力矩、偏航力矩。

图1 地面坐标系与机体坐标系关系

作用在无人直升机上的力和力矩是分析其动态特性的基本因素，决定了其基本性能。无人直升机的动力学方程可以由牛顿-欧拉方程推导出来[9]。

2 ADRC控制器设计

无人直升机在运动过程中受到干扰会使控制器的性能下降。因此，干扰抑制是航空系统安全飞行控制的一个主要考虑因素。自抗扰控制（ADRC）是一种通过设计鲁棒控制器来估计并消除干扰的控制方法[10]。

ADRC 主要由3 个模块组成：扩张状态观测器（ESO）、跟踪微分器（TD）和非线性状态误差反馈控制律（NLSEF）。ESO 是整个ADRC 的关键环节，它的主要功能是对未建模的动态、各种扰动进行实时的估算，以补偿系统中的不确定性。TD 的实现主要是对转换过程进行规划，并对差分信号进行合理的提取，提升对系统输出跟踪的速度。NLSEF 通过与干扰估算的补偿量相结合产生控制信号，提升系统的控制精度。图2所示为ADRC控制器的控制结构。

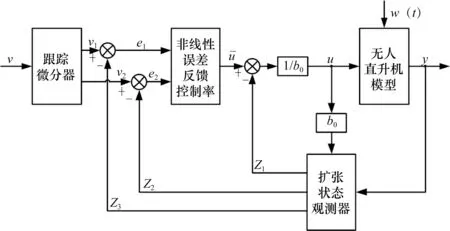
图2 ADRC控制器控制结构

扩张状态观测器的主要原理是根据状态观测器测得的系统输入和输出得到系统内部的状态量，在此基础上，引入一种新的状态变量，此状态变量是系统输入与扰动的结合，利用反馈机制对其进行观察，作用在输出上，有效地抑制扰动对系统的影响。

构造一个状态观测器，称为扩张状态观测器，形式为：

式中β01、β02、β03均为观测器的增益，对应不同的问题，可以选择不同的增益值，为了计算方便，观察器增益可以线性化，将fe和fe1替换成e。

跟踪微分器的主要作用是提供一个过渡过程，使不跳变的值能合理地跟踪跳变的值。将v(t)作为待微分的输入信号跟踪微分器：

式中r为时间因子。

非线性反馈控制律不同于线性反馈律，线性反馈律难以解决快速响应与系统超调之间的矛盾，满足不了系统的高性能要求，而非线性反馈控制律（NLSEF）则通过非线性反馈结构将状态误差组合在一起，不仅提高了系统的控制性能，还通过ESO 的扰动补偿，实现了动态补偿线性化。

二阶系统NLSEF的离散算法可表示为：

当α＜1 时，误差可以在有限时间内更快地达到零，同时α还可以显著地降低稳态误差，使其达到可以避免积分控制的程度。一种极端情况是α= 0，它可以带来零稳态误差，而PID中没有I项。正是由于非线性反馈的这种有效性和独特性，这种fal和fhan形式的非线性反馈函数在自抗扰控制框架中发挥着重要作用。

3 改进的粒子群优化遗传算法

ADRC 参数对系统控制性能有直接和重大的影响，因此有必要调整每个设计的ADRC 的参数，以确保提供适当的控制信号。ADRC 有很多可调整的参数，通常由经验方法确定，这对控制系统的准确性有很大的影响，导致控制器精度下降并出现超调现象。为了对控制器的性能进行优化，需要对ADRC 的参数进行整定，得到更好的控制器参数。

粒子群算法（PSO）的灵感来源于鸟群的社会行为，是一种基于种群的，以模仿鸟类种群为原型，将觅食过程转化为寻找问题最优解的算法[11]。PSO 算法的优化过程简单、高效，在复杂的搜索范围内，可以寻找出最优区域，因此在函数优化问题中得到了广泛的应用。

首先，算法需要设置一定数量的粒子和种群，将每个粒子作为一个解，并给出其速度和位置的信息，通过其适应度函数可以求出适应度值。适应度函数是体现粒子运动状态的重要指标，可根据控制器的特性或系统的响应误差进行设置，适应度值作为粒子优化过程的终止条件，决定了优化性能的好坏。运动空间中粒子位置和速度的变化不仅与惯性权重w、加速度因子c1和c2、随机常数r1和r2有关，还与两个极值参数密切相关，粒子速度和位置的更新公式如下：

式中：v为粒子的速度；x为粒子的位置；w为惯性因子；t为迭代次数；c1为粒子跟踪个体极值的加速度因子；c2为粒子跟踪全局极值的加速度因子；r1和r2为[]0,1 范围内的随机数；Pt和Gt分别为当前搜索的个体极值和全局极值的最优位置。

遗传算法具有自适应性强、可扩展、易实现等特点[12]。遗传算法的适应度函数在算法的每次迭代中选择最合适的个体方面起着重要作用，迭代次数少，会使优化性能降低，而过高的迭代次数会增加计算成本，所以，选择合适的适应度函数是遗传算法的关键之一。如果在进化过程中不考虑突变，那么将没有新的信息可用于进化，如果在进化过程中不考虑交叉，那么该算法可能会导致局部最优。但是遗传算法也存在过早收敛等问题，过早收敛会导致等位基因的丢失，从而难以识别基因，得到的结果是次优的。

改进的粒子群优化遗传算法（IPSO-GA）是在粒子群算法和遗传算法的基础上设计的。经典PSO 算法在求解过程中，由于过于依赖系统的惯性因子和加速度因子，难以产生最优解，且收敛速度缓慢。所以，为了提高PSO 的收敛性能，需要对PSO 的惯性因子进行非线性改善。优化的方程为：

式中：k为当前的迭代次数；kmax为最大的迭代次数；wmax和wmin分别为惯性权重w的初始值和结束值，基于经验法，一般取wmax= 0.9，wmin= 0.4。随着迭代次数的增加，其惯性因子w由0.9 逐步降低至0.4。在w较大时，算法在初始阶段拥有很好的全局寻优能力，在w较小时，算法的全局寻优能力减弱，局部寻优能力增强。这样的设置可以解决粒子群算法在后期局部搜索能力较差的问题。

加速度因子也是影响算法收敛速度的关键因素，对加速度因子c1和c2进行优化，优化的方程为：

式中：c1min和c1max分别为c1的最小值和最大值；c2min和c2max分别为c2的最小值和最大值。

因此，参数w、c1、c2的变化曲线如图3 所示。随着迭代次数的增加，c1从2逐渐减少到0.4，c2从0.4逐渐增加到2。在初始阶段代表个体极值的加速度因子c1较大，使个体极值的寻优更加快速，避免算法陷入局部最优。随着迭代次数的增加，c1逐渐减小，c2逐渐增大，增强了算法的群体寻优能力，可以加快算法的收敛速度。

图3 参数变化曲线

与粒子群算法相比，遗传算法在群体多样性方面表现出了更大的优势，本文提出的算法将遗传算法中的交叉、变异运算引入到粒子群算法中，以提高种群的多样性，从而解决了粒子群算法的局部最优问题。

交叉操作如下所示。

被交叉的个体：

由于粒子发生了突变，它们可能会超过极限。当粒子不在规定的范围内时，即X′ij＜Xjmin或者X′j＞Xjmax时，设置越过边界的方程如下：

式中：Xjmin和Xjmax分别为第j个变量范围内的最小值和最大值；X″ij为被调整的变量。

4 基于IPSO-GA的ADRC控制器设计

本文选用ADRC控制算法进行控制器的设计，ADRC虽然能够解耦原有系统，提供了很强的鲁棒性，但在多变的情况下仍然不可取，因为静态参数无法调整和应对各种情况。因此，需要采用一组可调参数来优化ADRC性能。ADRC 的参数包括来自TD 的r，来自ESO 的β01、β02、β03和来自NLSEF 的k1、k2，通常根据经验设置r=0.000 1h，因此每个ADRC需要优化5个参数。

在姿态控制器中，给定参考指令信号φr、θr、ψr均为5°的控制量。ADRC 适应度函数优化过程如图4所示。由图中可以看出，在优化过程中，适应度值是递减的，IPSO-GA 不断寻找更好的参数，当迭代次数达到25 时，函数曲线逐渐稳定，最终目标函数值为3.935 6。IPSOGA 整定的姿态角通道参数如表1 所示。姿态角的响应曲线如图5 所示。由图可知，每个通道的响应时间都在1 s以内，且3 条响应曲线的超调量较小。说明IPSO-GA 整定的ADRC姿态控制器响应速度快，稳定性高。

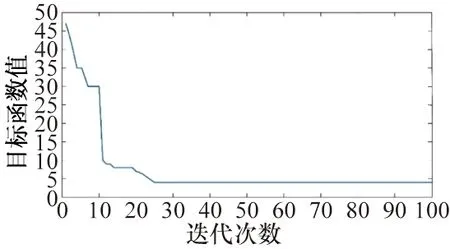
图4 ADRC姿态控制器中适应度函数优化过程

表1 姿态控制器参数

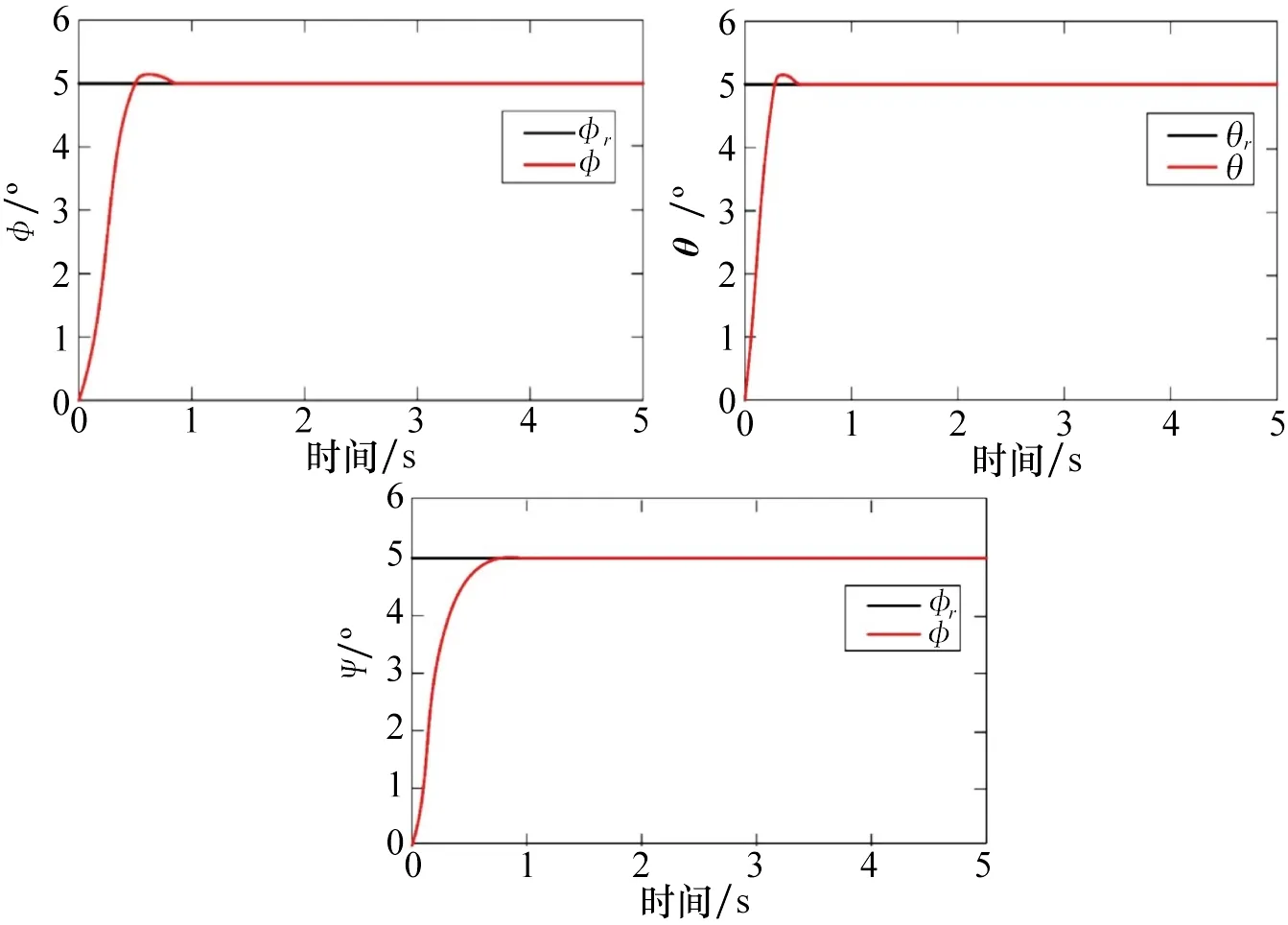
图5 姿态响应曲线

为了验证经过IPSO-GA 参数整定后ADRC 控制器的效果，本文基于MATLAB/Simulink 仿真平台，针对二阶控制系统，分别对ADRC 控制器和基于IPSO-GA的ADRC 控制器输入单位阶跃信号，系统响应曲线如图6 所示。图6（a）是理想环境下的输出曲线，图6（b）是系统引入白噪声后的输出曲线。从仿真图像可以看出，通过IPSO-GA 优化的ADRC 控制效果得到了显著提升，控制效果明显优于ADRC 控制器，使控制系统可以在更短的时间内达到稳定状态，稳定性增强，响应速度显著提高。

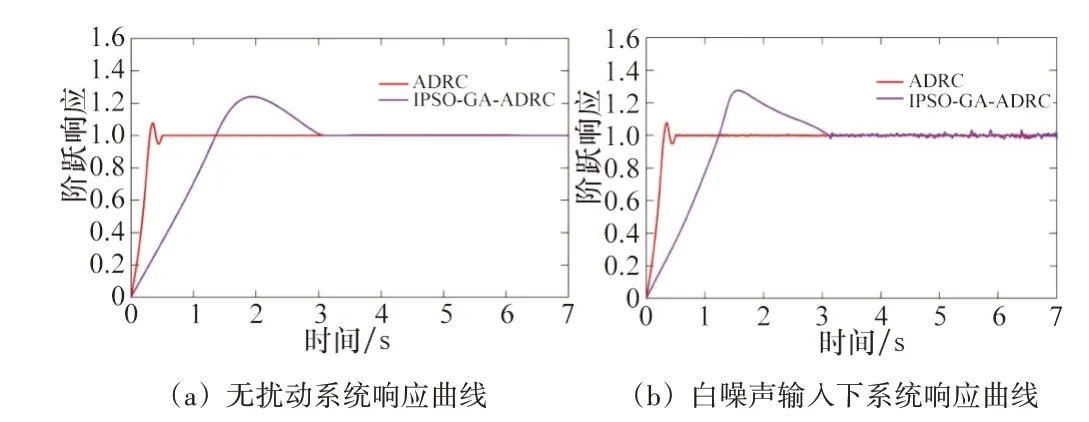
图6 系统响应曲线

针对ADRC 参数影响无人直升机控制性能且难以调整的问题，提出一种基于IPSO-GA 的ADRC 控制策略。通过理论分析、仿真和实验研究，得出以下结论。提出的IPSO-GA 改善了PSO 容易陷入局部最优的情况，增强了全局搜索能力，提高了算法的稳定性。通过IPSO-GA对ADRC 参数进行整定，仿真结果表明，所提出的策略使ADRC 控制器对无人直升机控制系统响应速度加快，减小了速度超调，还提高了控制系统的抗扰动性能，增强了稳定性。

5 结束语

本文针对无人直升机复杂的结构以及高耦合、非线性、时变的特性，采用机理建模的方法进行无人直升机的建模，建立机体坐标系和地面坐标系并进行坐标转换。通过牛顿-欧拉方程推导无人直升机的动力学方程，成功得到无人直升机的飞行动力学数学模型。基于建立好的模型设计ADRC 控制器，为了使控制系统的性能更加优秀，需要对ADRC 控制器的参数进行整定，得到更好的控制器参数。本文提出了一种改进的粒子群优化遗传算法，基于此算法设计ADRC 控制器，对无人直升机参数进行整定，基于MATLAB/Simulink 仿真平台进行数值模拟，并与参数整定前的ADRC 控制器进行比较，仿真结果表明，基于IPSO-GA 算法的ADRC 控制系统在控制性能上更加优秀。