线型静电纺丝泰勒锥自组织成形影响分析*

邢 升，周海迎，黄俊杰

（东华理工大学机械与电子工程学院，南昌 330013）

0 引言

聚合物纳米纤维在军工、环境、医疗和新能源等领域的应用研究取得了显著进展，其高质量、低成本宏量制备方法研究引起很多学者的关注[1]。线型静电纺丝具有结构简单、工作稳定、易拓展等特点，具有很好的应用前景[2]。泰勒锥形态和密度是影响纳米纤维质量和产量的关键因素，对其开展研究有助于调控线型静电纺丝过程。文献表明，由于Plateau-Rayleigh 不稳定性特性，小型圆柱元件表面的液体射流和液体薄膜是不稳定的，在液体表面张力作用下会分解成一系列的小液滴[3]。这种现象在纤维制造、金属丝涂层、静电纺丝、燃料电池、光纤、外科纺织品和雾/液滴过滤等领域得到了广泛的应用[4]。当圆柱形元件上附着液膜时，通常会观察到液膜自发破裂形成液珠，并以规则的间隔附着在元件上，甚至当液体与固体元件间的接触角明显为零时，这种液膜破裂形成液珠的现象也可能发生[3]。过去几十年里，众多国内外科研工作者深入展开了多方面的研究[5-6]。Plateau[7]和Rayleigh[8-9]提出圆柱形元件外表面上形成的涂层薄膜存在一定正曲率和负曲率区域，正、负曲率区域存在一定压力差，从而产生了由于压力梯度导致的流体流动[10]。这种内部通量导致位移振幅的增长，最终形成泰勒锥。Goren[11]讨论了金属丝上和小管内的环形液体涂层在自由表面毛细力作用下的不稳定性，并证明了Ohnesorge 数在各扰动中起关键作用。Yarin[12]提出了受电场影响的液滴稳定形状的理论，当液体表面达到喷丝前的临界状态时，其形状接近于半角为33.5°的圆锥体。

本文主要是基于自主改进并搭建的线型自由液面静电纺丝实验装置，考察了聚合物溶液浓度、工作电压、旋转速度和电极丝直径这4 个主要工艺参数对聚合物泰勒锥成形及其线密度的影响，并分析了单个工艺参数对聚合物泰勒锥成形的影响。研究结果可为后续的实验装置改进与实验设计优化提供一定的思路，为线型自由液面静电纺丝装置的深入研究提供参考。

1 实验部分

1.1 试剂与仪器

聚偏二氟乙烯（Poly Vinylidene Fluoride，以下简称PVDF），P302009-100g 型，上海阿拉丁生化科技股份有限公司；N-N-二甲基甲酰胺（N，N-dimethylformamide，以下简称DMF），纯度大于99.5%，上海阿拉丁生化科技股份有限公司；去离子水，W119424-25L 型；数显恒温磁力搅拌器：型号85-2B，山东欧莱博仪器有限公司；高压电源：型号DW-P104-5ACB2，最高输出电压为100 kV，东文高压电源（天津）股份有限公司；电子天平：MTB 2000，深圳市美孚电子有限责任公司；拍摄相机传感器：索尼IMX707，分辨率3 840×2 160，最大帧率60帧/s，传感器尺寸1/1.28 inch，f/1.9光圈。

1.2 实验过程

PVDF/DMF 溶液配置：称取一定质量的PVDF 药品和溶剂DMF 按照一定的比例混合，样品放置于恒温磁力搅拌器中搅拌，设置恒温60 ℃，加热搅拌时长约为3 h，得到澄清透明溶液，放置于室温下，静置去除气泡后备用。

1.3 测试与表征

采用相机测定待测溶液实验过程中泰勒锥成形情况，恒定帧率60 帧/s，分辨率3 840×2 160，每组实验拍摄3 min。

1.4 线型自由液面静电纺丝装置及电纺过程

图1 所示为自制线型自由液面静电纺丝装置示意图，主要包括电极丝、溶液槽、收集板、齿轮传动装置、电机、辊筒、相机等。实验过程中，3 根呈120°分布的铜丝安装在金属轴上，金属轴连接上带轮，带轮与一个由直流电机驱动的皮带相连，使用调速器控制电机，以实现辊筒的转速控制。

图1 线型自由液面静电纺丝装置

实验过程中，高压电源正极连接收集板，负极连接电极丝和辊筒。当电极丝通过聚合物溶液浴时，溶液挟带在电极丝上，形成一层溶液薄膜覆盖在导线上。由于瑞利-泰勒不稳定性，溶液薄膜在电极丝上分解成单个的带电聚合物液滴。图2所示为实验过程中液滴成形图；图3所示为实验过程中泰勒锥成形图。

图2 液滴成形

图3 泰勒锥成形

1.5 响应面法与实验设计

本实验设计基于响应面法（RSM）可以量化测量到的响应与多个重要输入因子之间的关系[13]。采用基于单因素法的响应面法进行实验设计。结果表明，泰勒锥自组织成形的影响因素包括以下几种：聚合物溶液浓度（wt%）、工作电压（kV）、旋转速度（r/min）和电极丝直径（mm），并考察了这4 个参数对泰勒锥成形直径的影响。各因子及因子水平如表1 所示。基于CCD，响应值（平均泰勒锥直径）与这4 个因子（A、B、C和D）之间的数学关系可以用如下的二次多项式模型近似[14-15]：

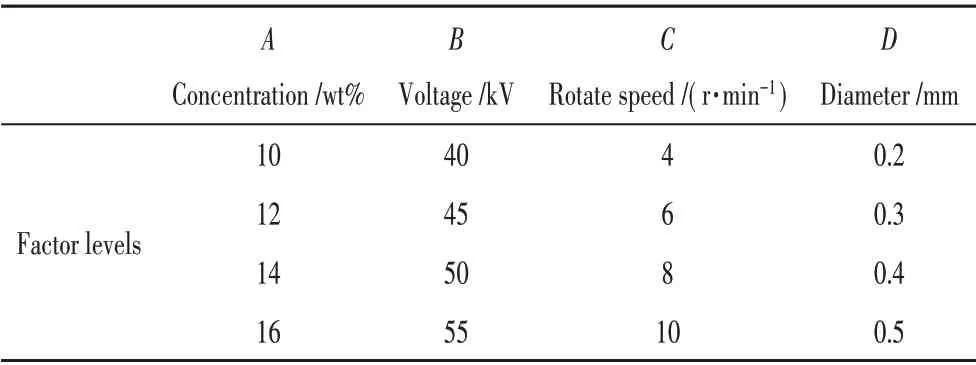
表1 实验因子与因子水平设计

式中：f为响应值；αn和βn（n=1，2，3，4，5）均为未知系数，通过实验数据确定。

每组实验过程拍摄3 min，所有实验均在常温（25±1）℃，相对湿度（42±3）%下进行。

2 结果与讨论

2.1 实验结果

采用相机测定了PVDF 泰勒锥成形形貌，用图像处理软件ImageJ 测量泰勒锥直径，测量每张照片上携带的全部泰勒锥直径，并统计其直径的平均值（MFD）、泰勒锥线密度（LD）和相对标准差（RSD），实验结果如表2所示。

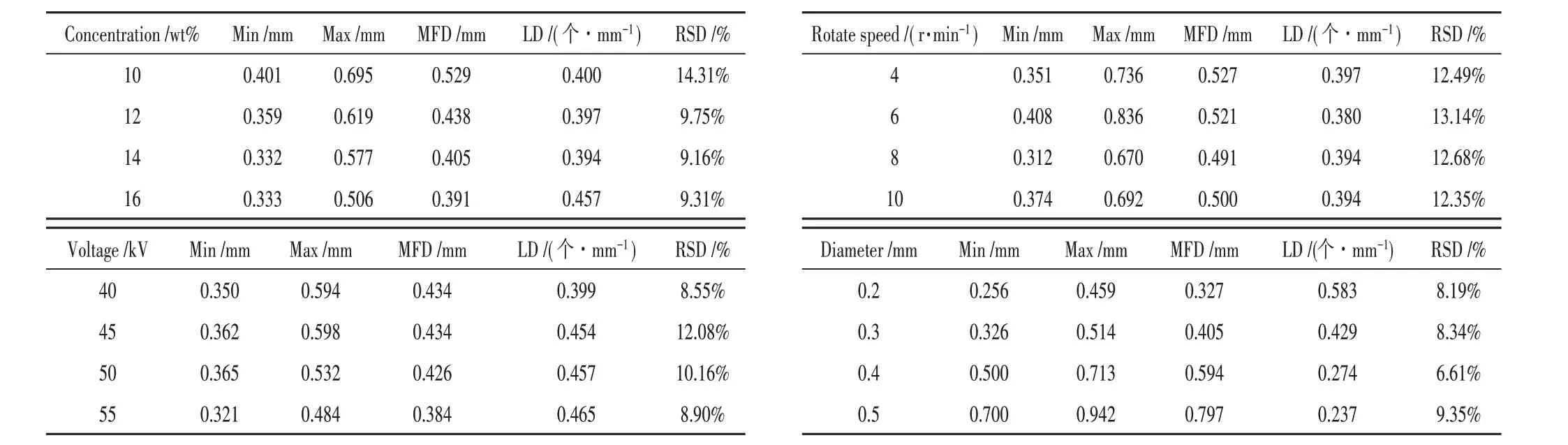
表2 实验结果

2.2 测试与表征

通过ImageJ 测量出的数据分别按顺序绘制成的泰勒锥直径分布如图4 所示。实验设计中PVDF 泰勒锥MFD范围为0.327～0.797 mm。

图4 泰勒锥直径分布

在考察聚合物溶液浓度对泰勒锥成形影响的实验中，浓度为10%的实验条件下，MFD 值最大，图5（a）为该条件下实验过程拍摄图；浓度为16%的实验条件下，MFD 值最小，图5（b）为该条件下实验过程拍摄图；浓度为16%的实验条件下，LD值最大，图5（c）为该条件下实验过程拍摄图；浓度为14%的实验条件下，LD值最小，图5（d）为该条件下实验过程拍摄图。于室温下，PVDF 溶液表面张力系数随着溶度的增大而降低，分析其原因在于图5（b）中溶液浓度较大，溶液表面层分子同时受到本相内分子和另一相分子作用[16]。由于两相分子性质不同，溶液表面层分子受力的球对称性被破坏，导致溶液的表面张力降低，因此观察到较为细小的泰勒锥，同时线密度也最大。

图5 浓度实验拍摄图

在考察工作电压对泰勒锥成形影响的实验中，工作电压为40 kV 的实验条件下，MFD 值最大，图6（a）为该条件下实验过程拍摄图；工作电压为55 kV 的实验条件下，MFD 值最小，图6（b）为该条件下实验过程拍摄图；工作电压为55 kV 的实验条件下，LD 值最大，图6（c）为该条件下实验过程拍摄图；工作电压为40 kV的实验条件下，LD值最小，图6（d）为该条件下实验过程拍摄图。在较低浓度时，PVDF 溶液的粘度随着电场强度的升高有一定程度的上升[17]，分析其原因在于图6（b）中的电压较大，其分子链运动的自由体积较大，在较大电场力的作用下，溶液表面电荷吸附力和活度增加，从而使泰勒锥表面张力减小，泰勒锥在成形过程中所需的克服表面张力的曲张扰动也较低，因此观察到较为细小的泰勒锥，同时线密度也最大。

图6 电压实验拍摄图

在考察旋转速度对泰勒锥成形影响的实验中，转速为4 r/min 的实验条件下，MFD 值最大，图7（a）为该条件下实验过程拍摄图；转速为8 r/min 的实验条件下，MFD 值最小，图7（b）为该条件下实验过程拍摄图；转速为4 r/min 的实验条件下，LD 值最大，图7（c）为该条件下实验过程拍摄图；转速为6 r/min 的实验条件下，LD值最小，图7（d）为该条件下实验过程拍摄图。旋转速度所得实验数据中，最大差值为6.83%，分析其原因在整个自由液面静电纺丝过程中电场力是主要驱动力，电场力方向由电极丝指向收集板，而由于辊筒旋转运动产生的离心力相较于由静电场产生的电场力较低，因而泰勒锥成形影响较小。

图7 转速实验拍摄图

在考察电极丝直径对泰勒锥成形影响的实验中，电极丝直径为0.5 mm的实验条件下，MFD值最大，图8（a）为该条件下实验过程拍摄图；电极丝直径为0.2 mm 的实验条件下，MFD 值最小，图8（b）为该条件下实验过程拍摄图；电极丝直径为0.2 mm 的实验条件下，LD 值最大，图8（c）为该条件下实验过程拍摄图；电极丝直径为0.5 mm的实验条件下，LD值最小，图8（d）为该条件下实验过程拍摄图。分析其原因在于电极丝直径变化不影响金属自身的表面自由能；而金属丝直径越大，电极丝经过溶液槽时挟带的溶液量越大，导致电极丝表面形成的液膜横截面积越大，泰勒锥在成形过程中所需的克服表面张力的曲张扰动也就越大，泰勒锥形成时的接触角也就越小，因此形成的泰勒锥直径越大，同时线密度也越小。

图8 电极丝直径实验拍摄图

2.3 响应结果分析

利用Design-Expert 软件对单因素实验数据进行方差分析得到结果如表3所示，建立PVDF泰勒锥的MFD（f）和聚合物溶液浓度（A）、工作电压（B）、旋转速度（C）、电极丝直径（D）的多元二次回归方程模型：

表3 工艺参数方差分析结果

为了研究模型的统计显著性，提出了概率值（P值），它表示因素的显著性。当P＜0.05 时，该因素对反应有显著影响。而当P＞0.05 时，该因素对反应没有显著影响。R2是另一个重要的因素，用于研究模型的统计显著性，它决定了模型对观察到的反应的适应程度。

由表3 可知，模型P＜0.05 说明电极丝直径对聚合物泰勒锥MFD 的影响较大，p＜0.000 1，说明此模型的差异较为显著，方程较为合理。对于MFD 来说，4 个影响因素：聚合物溶液浓度（A）、工作电压（B）、旋转速度（C）、电极丝直径（D）中，电极丝直径对聚合物泰勒锥MFD 影响最大，随后是聚合物溶液浓度的影响，而旋转速度对聚合物泰勒锥MFD 的影响程度较低。综上，4 个因素对MFD影响大小顺序为电极丝直径（D）＞聚合物溶液浓度（A）＞工作电压（B）＞旋转速度（C）。

泰勒锥预测与实际平均直径如图9所示。

图9 泰勒锥预测与实际平均直径

图10 为泰勒锥MFD 3D 响应面图，由图可以看出，泰勒锥MFD 受电极丝直径影响最大，呈同步增大趋势；聚合物溶液浓度和工作电压影响较小，泰勒锥MFD 与之呈反比关系；旋转速度对泰勒锥MFD影响较小。

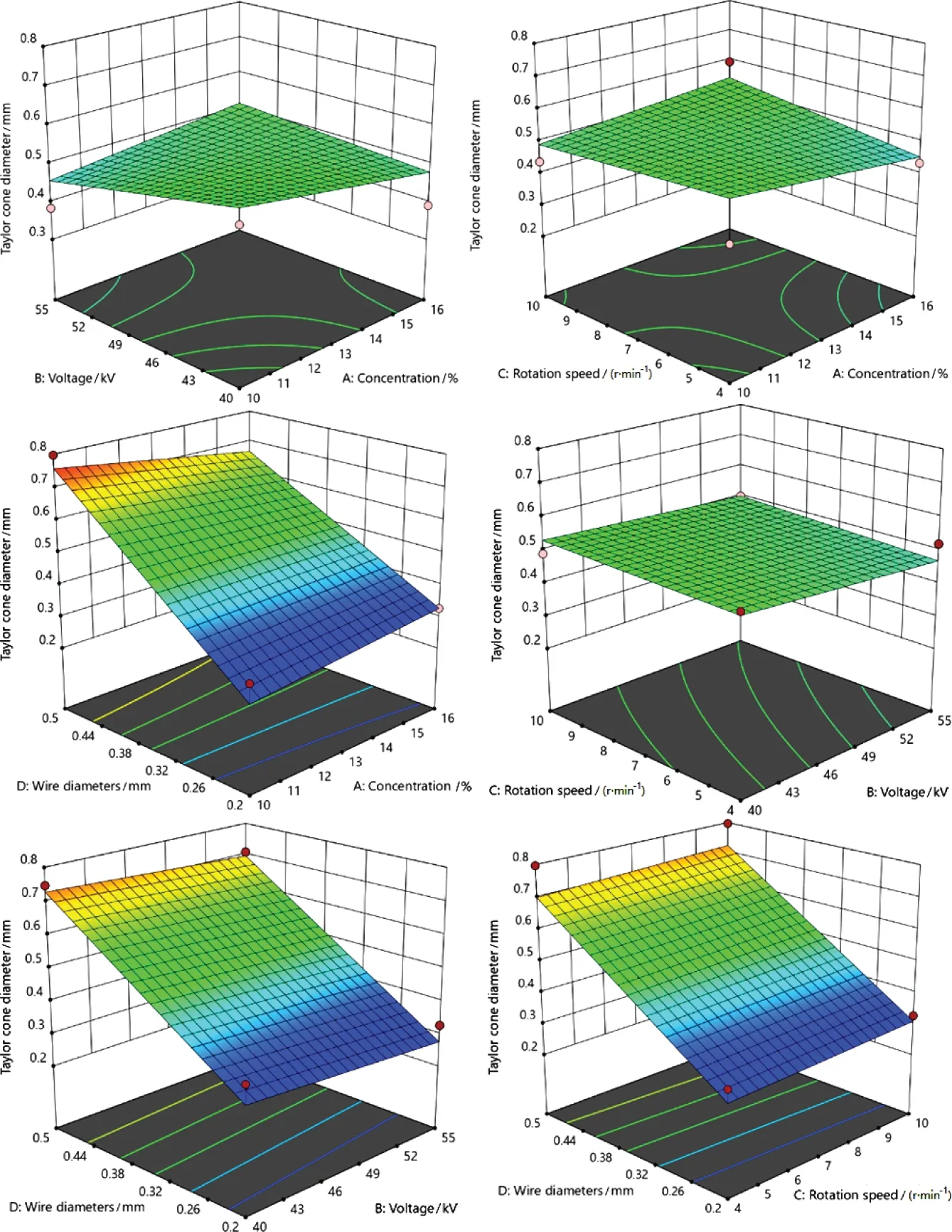
图10 泰勒锥MFD 3D响应面图

2.4 液滴成型模拟

为了说明实验现象，探究线型自由液面静电纺丝过程中聚合物溶液泰勒锥自组织成形。利用Comsolmultiphysics 模拟了不同聚合物溶液浓度、工作电压和电极丝直径条件下液滴的成形情况，通过分析液滴成形过程中压力分布，进而推断泰勒锥自组织成形。图11（a）为不同电极丝直径下的液滴二维压力等值线图，图11（b）为不同聚合物溶液浓度下的液滴二维压力等值线图，图11（c）为不同工作电压下的液滴二维压力等值线图。压力等值线图显示压力大小趋势从液膜正曲率区域到液膜负曲率区域为由大到小。结果显示，电极丝直径对聚合物液滴直径有较大影响，聚合物溶液浓度和工作电压对聚合物液滴直径影响较小。流体压力随电极丝直径的增大而减小，导致液滴直径随增大，但液滴线密度明显降低；流体压力随着工作电压的增大有少许增长，导致液滴直径降低，液滴线密度有少量增加；流体压力在溶液浓度为14%时达到最大，因而此时液滴线密度最小，而溶液浓度为16%时，液滴直径最小。流体模拟结果与相机观察到的实验结果相一致。分析其原因在于电极丝表面粗糙度引起的拉普拉斯压力差驱动液体向低压力的区域集中，最终出现液膜破裂，聚并形成液滴。

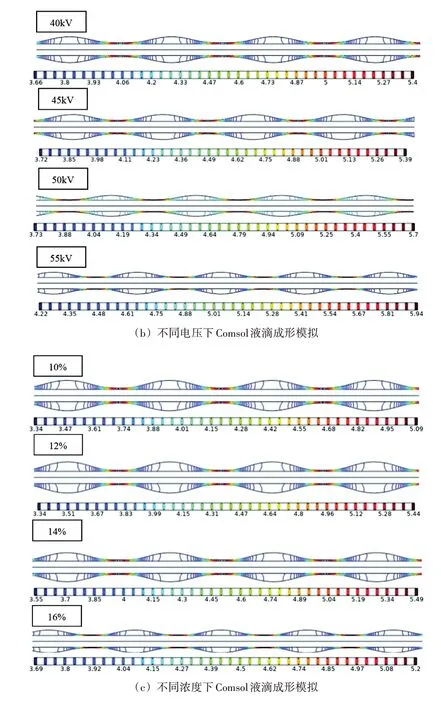
图11 Comsol液滴成形模拟

3 结束语

本文采用一种自由液面的静电纺丝装置来替代传统电纺中的毛细管喷丝。设计实验并考察了4 个主要工艺参数对聚合物泰勒锥成形的影响，结果表明：

（1）一定条件下，聚合物泰勒锥MFD 随着聚合物溶液浓度、工作电压的增加而减小，随着电极丝直径的增加而增大，受喷头转速影响较小；

（2）通过响应面法建立了工艺参数与聚合物泰勒锥尺寸间的多元二次回归方程模型，量化了响应与输入间的关系；

（3）利用Comsolmultiphysics 模拟了不同条件下液滴的成形情况，模拟结果与实验结果相符。

然而，目前线型自由液面静电纺丝过程中还有很多现象和机理亟待研究。因此，还需要进一步探究纺丝过程中各实验参数对实验的影响。