基于分数阶PID机器人自动行驶误差分析*
彭 琳,唐德文※,陈 钢
(1.南华大学机械工程学院,湖南衡阳 421001;2.核设施应急安全技术与装备湖南省重点实验室,湖南衡阳 421001)
0 引言
近年来随着电动轮小机器人的发展,采用电机直接驱动车轮的方式也越来越普遍,这种方式具有较高的传动效率,便于独立控制且响应迅速等优点,非常有利于动力学控制。更适合未来的小机器人往智能及环保化发展[1]。与此同时,小型轮式机器人的直线行走PID控制技术在自动控制领域已经有了长足的发展,取得了巨大的进步[2]。
目前,针对自动行走的控制问题,科研工作者基于经典及现代控制理论已经提出多种控制方法,使用这些方法以减小自动行走的误差,Ossama Mokhiamar 与Masato Abel[3]研究了车辆运动时车轮纵向和侧向合力的最优分布,改善了侧向加速度和横摆角速度的响应速度,得出了性能加权函数能对车辆运动稳定性产生影响。E Esmailzadeh 等[4]建立了二自由度的车辆模型,该模型以横摆角速度和质心侧偏角作为状态变量。以横摆力矩为最优控制系统求出了其与车辆状态参数之间的函数关系,并研究了不同参数对控制效果的影响。北京理工大学的舒进、陈思忠等[5]应用物理学知识、理论力学知识推导出了在进行侧向和横摆两种运动时的二自由度方程。并推导出了前轮偏角与横摆角速度和质心侧偏角之间的传递函数。
以上研究对轮式机器人运动误差分析取得了良好效果,但在复杂工况下轮式机器人受横向和侧向的信号干扰,采用常规的PID 控制系统,轮式机器人运动时的横摆角速度与质心侧偏角这两个不同的变量虽可以同时得到控制,但其控制的精度仍然不够精细[6-7]。为此,本文提出一种采用分数阶PID 的控制策略,建立基于分数阶PID 横摆角控制系统的仿真模型,分析轮式机器人在不同工况下运动时的速度、角加速度、位移等,使轮式机器人可在复杂环境下运动可控,极大地提高了机器人的动态性能和鲁棒性。
1 动力学模型
基于不同的考虑因素,可有针对性地选择不同的自由度来分析机器人行驶系统中的不同问题[8]。然而自由度过高会导致建立的运动模型过于复杂,不利于运动微分方程的建立,故本文采用两自由的机器小车模型,在两自由度的模型下,机器人运动时会产生不同的横摆角速度,转向控制器将实际横摆角速度与理想横摆角速度的差值作为输入,在传统PID 控制理论上加入分数阶控制理论,使其在整数阶控制的基础上增加了积分阶次和微分阶次两个可变的参数,使得参数设置更加精确细致。如图1所示。

图1 两自由度小车运动模型
机器人轮式行走机构几何中心点O的位置和姿态,对式(1)积分,则有:
式中:VL为左轮速度;VR为右轮速度;B为轴距;θ为运动方向与X轴夹角。
式中:(x0,y0,θ0)为机器人几何中心点O在t=0 的时刻的位置姿态;(x,y,θ)为机器人几何中心点O当前的位置与方向。
故机器人行走机构的线速度和角速度可以表示为:
式中:v为线速度;θ˙为角速度。
在确定轮式机器人的基本结构的基础上,可以通过控制机器人两侧的永磁同步电动机的转速来控制机器人的运动,实现控制机器人线速度、转向角速度、转向角度等[9-11]。机器人运动时的受力如图2所示。

图2 机器人运动受力

式中:αf为左轮侧偏角;αf为右轮侧偏角;Lf为左轮到质心的距离;Lr为右轮到质心的距离;ωr为横摆角速度;δf为左轮转角;δr为右轮转角。
可以得到机器人的运动微分方程为:
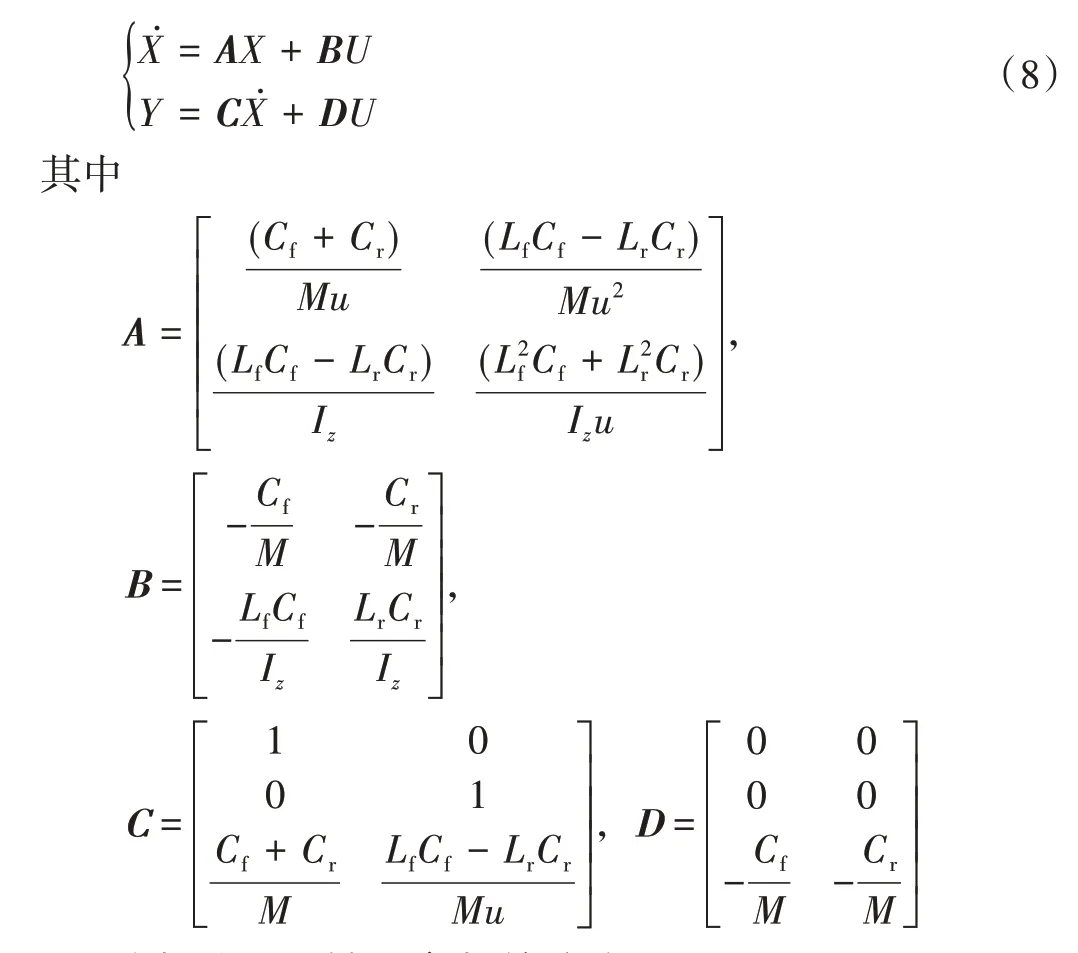
2 分数阶PID控制参数的确定
分数阶PID 控制原理实际是用分数阶环节替代传统的PID 控制器的比例环节,优化系统的传递函数,使得整个控制模型在PID 控制的优点上,有更好的动态响应性能和扰动抑制能力。在本文的研究中,首先预设一个理想横摆角速度模型,再将分数阶PID 控制器控制下的机器人实际横摆角速度与理想横摆角速度的值做差,再将实际值与理想值相叠加,最后将叠加值作为输入,反馈回分数阶PID 控制器,由控制器的输出反馈给机器人,进而实现对机器人质心侧偏角、横摆角速度和侧向加速度及侧向位移的控制[12-13],如图3所示。

图3 机器人控制系统原理
因为PIλDμ控制器是分数阶PID 控制的核心,所以首先建立PIλDμ控制器。PIλDμ控制器的控制时域表达式为:
式中:λ为控制器积分项的阶次;μ为控制器微分项的阶次;KP为比例系数;KI为积分系数;KD为微分系数。
对上式进行拉普拉斯变换,得到分数阶PID 控制器的传递函数:
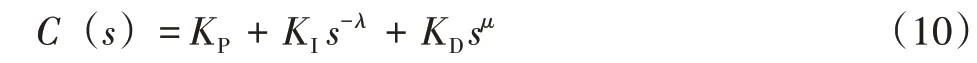
分数阶PID 控制器中的闭环控制系统被控对象的传递函数将决定其参数的整定,为了实现这个过程,需要推导出实际和理想横摆角速度的传递函数。而上文推导的机器人轮式行走机构二自由度的运动学微分方程恰恰可以得出横摆角速度与两轮转角的关系。由此,对运动学微分方程进行拉普拉斯变换可得横摆角速度对后轮转角的传递函数:

式中:σ为稳定度;ζ为阻尼比。
考虑到ζ搜索范围对系统性能的影响并不大,所以ζ的取值不需要特别精确,选取ζ=0.5。设定[0.4,5]为σ的范围,设定0.1为系统的步长。确定σ值的原则是系统单位阶跃响应的时间平方加权误差平方积分最小。此时如果系统始终保持稳定,则代表σ的值可行,系统稳定后便可以由此来确定极点。若系统无法保持稳定,则需要KP的值不断调整优化,直到系统稳定。在确定完极点和比例系数后,再用相同的方法整定其他的控制参数。
(3)确定λ、μ第i次搜索范围i∈[1,4]。当i=1时,μ∈[0.1,1]、λ∈[0.1,1],取 步 长Δi= 0.01;i>1,μ∈[max(Δi,μi-1-2μi-1),(μi-1+2μi-1)],λ ∈[max(Δi,λi-1-2λi-1),(λi-1+2λi-1)],Δi=Δi-1/10
(4)随着5 个参数的值第i次确定完。使用得出的5个参数完成特征方程的构建,若4 个指标均能满足控制系统的要求,则表示完成了参数整定的过程;若仍有指标无法满足系统的控制要求,则要重新选取最接近指标的λi、μi值,并使其在原有基础上累加,重复上述步骤;若i>4后仍不满足,则需重新确定5个参数,然后重复上述方法。
在确定完λ、μ值后,使用分数阶PID 控制系统的Outaloup[14]近似求解法,该近似求解的算法原理是对G(s)=(s/ωn)α传递函数取近似值,并通过构建滤波器来最终实现微积分近似求解,由于分数阶微积分的计算不能在实际应用中直接实现,而分数阶PIλDμ控制器的核心就是微积分算子sα的有理化,解出控制系统控制器的积分项和微分项,即:sλ=G1(s)、sμ=G2(s)。在构建滤波器求解时,只考虑频率段(φb,ωh)[15],其中,φbωh=1。该频率段为中间频率段,在该频率段可以构建出连续滤波器的传递函数为:

由MATLAB/Simulink 软件实现滤波器的设计,滤波器的N值决定其精度,当N值越大,控制精度就会越高,但往往计算也会更加复杂,控制信号经由滤波器实现α阶的微积分计算,就能实现分数阶PID的控制效果。
3 基于MATLAB/Simulink 仿真
仿真采用的模型参数如表2所示。
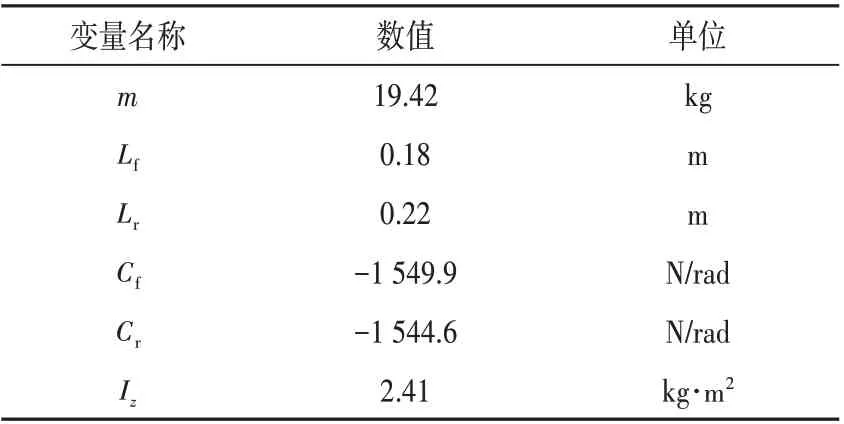
表2 仿真模型参数
为了便于仿真,接下来的仿真实验选择对车轮转角阶跃输入进行分析,进而来分析轮式机器人的行驶稳定性[16]。取机器人行驶速度为0.8 m/s,取行驶时的阶跃信号幅值为0.1 rad。建立MATLAB/Simulink 仿真模型,如图4~5所示。输入相应的仿真参数进行计算,随后得到横摆角速度、侧向加速度、质心侧偏角、侧向位移4 个物理量的响应曲线。将在分数阶PID 控制下得到的仿真响应曲线与PID控制下的行驶数据仿真曲线相对比。

图4 PID控制系统仿真模型

图5 分数阶PID控制系统仿真模型
仿真相应对比曲线如图6~9所示。由图6~7可以看出,分数阶PID 控制的自动行驶系统的横摆角速度达到稳定值的响应时间比PID 控制下所需要的时间更短,机器人的横摆角速度降低了23.6%,侧向加速度降低了22.1%,机器人的行驶稳定性和循迹能力得到了明显提高。

图6 横摆角速度的响应曲线

图7 侧向加速度的响应曲线
由图8 可以看出,分数阶PID 控制的自动行驶系统下机器人的质心侧偏角在经历2 s左右的波动之后基本保持为0,不论是响应时间还是侧偏角超调量都要小于PID控制,侧偏角超调量更是降低了71.4%明显提高了机器人在行驶时的运动稳定性。
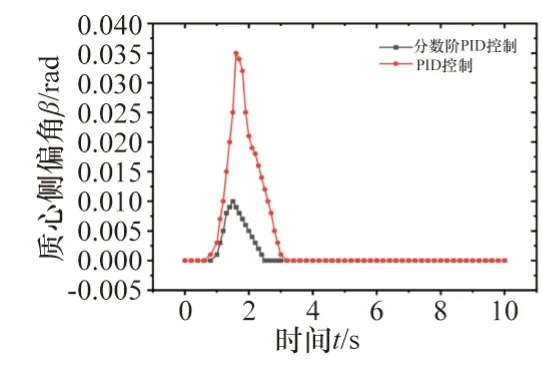
图8 质心侧偏角的响应曲线
由图9可以看出,在同样的行驶距离下,分数阶PID控制的自动行驶系统下机器人的侧向偏移量明显比PID控制下的机器人降低了29.5%,提高了机器人保持直线行驶的能力,改善了控制的精确性。

图9 侧向位移的响应曲线
4 结束语
本文针对常规PID 控制精度不够的情况,设计了分数阶PID 控制策略,构建了基于分数阶PID 横摆角控制系统的仿真模型并采用MATLAB/Simulink 联合仿真对控制效果进行仿真验证,并将仿真结果与PID 控制仿真结果相比较,主要结论如下。
(1)与PID 控制相比,使用分数阶PID 控制的机器人自动行走时的横摆角速度降低了23.6%,侧向加速度降低了22.1%,机器人行走时的运动稳定性有很大改善。
(2)与PID 控制相比,采用分数阶PID 控制的自动行驶机器人的质心侧偏角也比PID 控制时降低了71.4%,可以得到更加优越的控制效果。
(3)分数阶PID 控制时机器人侧向位移的位移量相比于PID 控制降低了29.5%。故在使用分数阶PID 控制方法作为控制策略时,机器人拥有更优越的控制效果,提升了小型轮式机器人的行驶稳定性。

