井下涡轮发电机叶片结构参数匹配分析*

席文奎，贾 超，孙东鑫，王科强

（西安石油大学机械工程学院，西安 710065）

0 引言

在钻井过程中，为实时掌握井下工况，需要利用随钻测量进行被钻地层信息的收集与反馈，因此可靠地向井下仪器和工具提供持续稳定的电能是非常重要[1]。目前，井下仪器供电方式主要是锂电池供电，由于小井眼钻井技术导致锂电池结构紧凑且容量十分有限，通常电池连续工作时间不超过200 h，无法满足井下仪器长时间大功率的电量需求；其次，电池的工作受环境影响大，难以适应井下高温、腐蚀、震动与撞击的恶劣环境[2]；另外，频繁地更换锂电池耗费人力物力且会给环境造成压力，不具有环保意义[3]。

相比较锂电池组供电方式，涡轮发电机能够适应井下高温高压等复杂环境[4]，并且井下涡轮发电技术属于流体机械范畴，实现井下泥浆动能转化为涡轮机械能再通过发电机转轴转化为电能的能量转化[5]。其中，导轮主要起导流作用，在机械结构中属于定子，而涡轮主要是通过叶片与流体介质相互作用，把流体的动能或压能转换为涡轮发电机的机械能，在机械结构中属于转子。故涡导轮叶片作为其中的关键部件决定井下涡轮发电机的性能好坏。涡导轮叶片结构优化的主要目的是提高发电系统的整体发电性能。因此，导轮与涡轮叶片结构的设计是提高涡轮效率的关键，决定整个涡轮发电机的效率。

国内外学者对涡轮发电机做了大量研究。Hoschek Josef[6]利用放样B样条来控制方程变量，采用牛顿插值法进行参数调整从而达到减小绘制图的误差范围，能更好地设计出叶片形状。贾惠芹等[7]通过建立涡轮模型，采用流体动力学软件Fluent 对涡轮的紊流流场进行仿真和分析，设计出体积小、性能优、效率高的小直径涡轮发电机。张晓东等[8]通过对不同叶型的导轮和涡轮组合的CFD流场分析，研究不同结构的导轮对涡轮性能的影响，基于BP 神经网络和Fmincon 函数与遗传算法结合的方法对叶片进行优化分析。李方韬等[9]采用滑移网格方法，编写UDF 对井下涡轮进行动态仿真，研究井下涡轮水动力性能的影响，并对井下涡轮的启动特性和运动过程进行了分析。

为提高发电效率，通过单因素实验对比不同叶片结构参数对速度以及流场的影响并进行响应曲面法优化参数，使涡轮发电机在相同条件下具有更高的效率，因此，开展泥浆涡轮发电机的叶轮性能研究具有十分重要的现实意义[10]。

1 涡轮发电机结构设计与流域划分

1.1 涡轮发电机整体结构

针对具体小尺寸钻井仪器工具供电方式，设计了一种涡轮发电机，整体结构采用磁耦合器连接方式，涡轮通过磁力耦合作用与发电机转子连接，省去了旋转动密封，不存在泄漏等动密封引起的不可靠因素[11]。总体结构如图1所示。泥浆泵将泥浆注入到井下时，泥浆经过定子导轮导流，高速流动的泥浆进入转子涡轮叶片流道，冲击叶片产生旋转力矩，带动转子涡轮高速旋转；转子涡轮通过磁力耦合装置带动转子轴旋转，从而驱动发电机组件的转子旋转，产生电能。

图1 涡轮发电机结构

1.2 涡导轮叶片模型建立

目前，直叶片和弯扭叶片是涡轮叶片的两大基本叶片形式，两者各有优劣，采取扭曲叶片会减少沿叶高冲角变化和径向流动能量的损失，选取弯扭叶片进行模拟实验。其中弯扭叶片的中弧曲线段如图2所示。

根据图2 坐标系中的曲线可以建立叶片变化方程为：

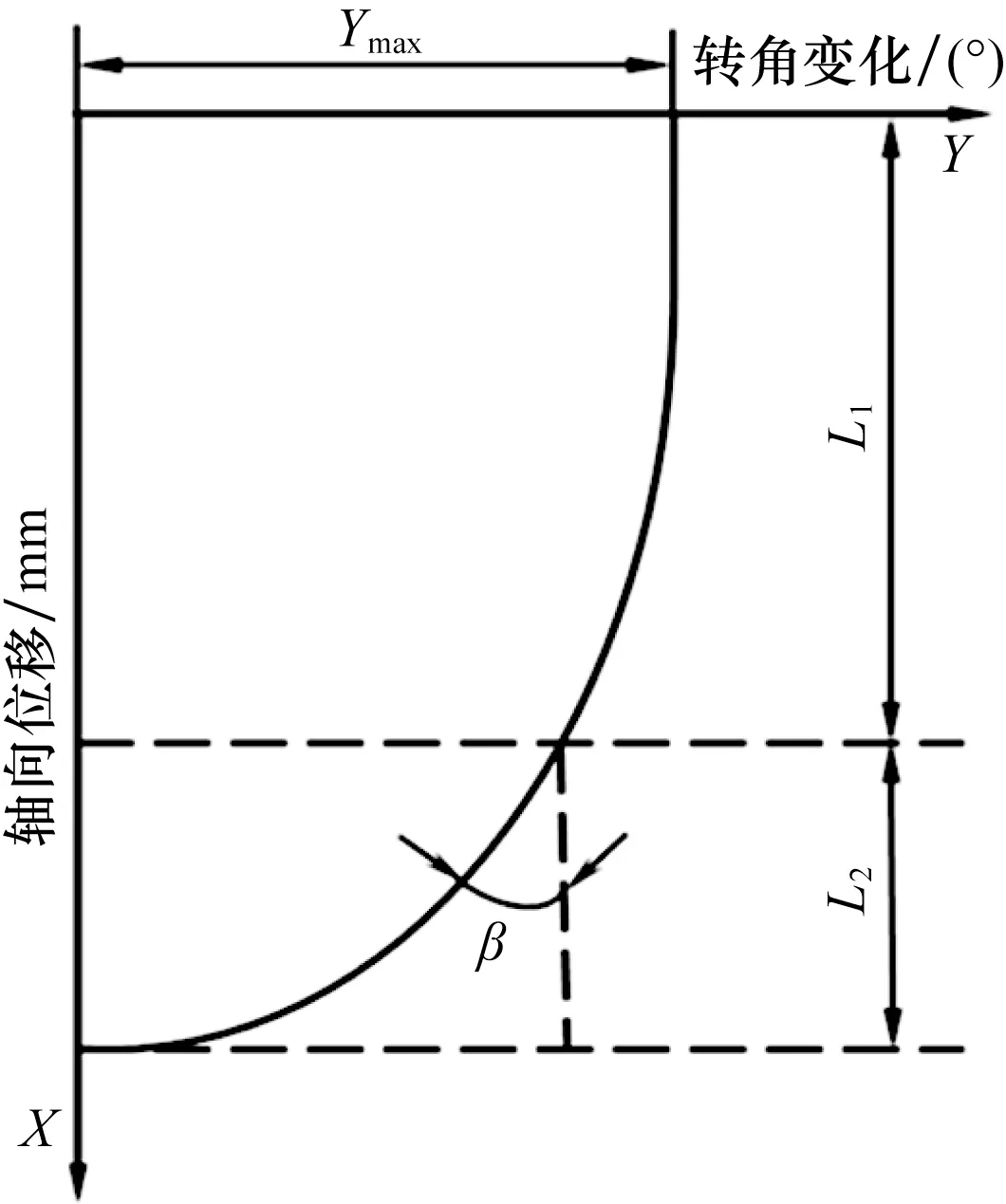
图2 中弧线过渡弯扭曲线

其螺旋升角为γ，螺距为S，涡轮外径为Dr，三者关系如下：

根据钻铤尺寸及涡轮工作强度要求，设参数如表1所示，由式（1）～（2）可得其螺距为220 mm。

表1 涡导轮结构特征

如图3 所示。采用1 个涡轮加1 个导轮的组合方式，钻井时，当井下泥浆经导轮导流驱动涡轮转动时，磁耦合器外磁钢和涡轮进行同步转动，利用磁性材料同性相斥、异性相吸的工作原理，磁耦合器内磁钢及固联的发电机转轴一起转动，转子在定子线圈中做切割磁感线运动并产生电能。

2 单因素实验

为确定涡导轮结构参数对效率的影响，需要进行单因素实验（控制变量法），将多因素问题简化为多个单因素问题。依据涡导轮结构不同，选取涡轮叶片数目Z1、涡轮螺旋升角β1、进口段长度L1、涡轮叶片厚度M1，对导轮结构选取导轮叶片数目Z2、导轮螺旋升角β2、出口段长度L2和导轮叶片厚度M2，在转速2 000 r/min、流速15 L/s 下效率最高。因此8 个结构参数在此条件下进行单因素实验，得到每个结构参数对涡导轮性能的影响。图4所示为单因素实验的结果曲线。

在第1 节建模的基础上进行单因素实验，其中取叶片数目5、7、9、11、13，分别取螺旋升角25°、35°、45°、55°、65°，分别取叶片厚度1.5、3、4.5、6、7.5 mm，分别取出口段长度4、12、20、28、36 mm。

如图4（a）所示，在5 叶片与7 叶片之间，导轮压差急剧下降，经过7 叶片后压差逐渐平稳递增，导轮速度一直平稳递增，没有太大的波动。涡轮压差在7 叶片周围有明显波动，在11叶片和13叶片之间，速度的变化最为明显，波动范围最大。

如图4（b）所示，导轮压差随着螺旋升角的增大逐渐地上升，导轮速度在35°～45°之间有明显的跃升。涡轮压差随着螺旋升角增大而逐渐减少，涡轮速度在55°附近有明显波动。

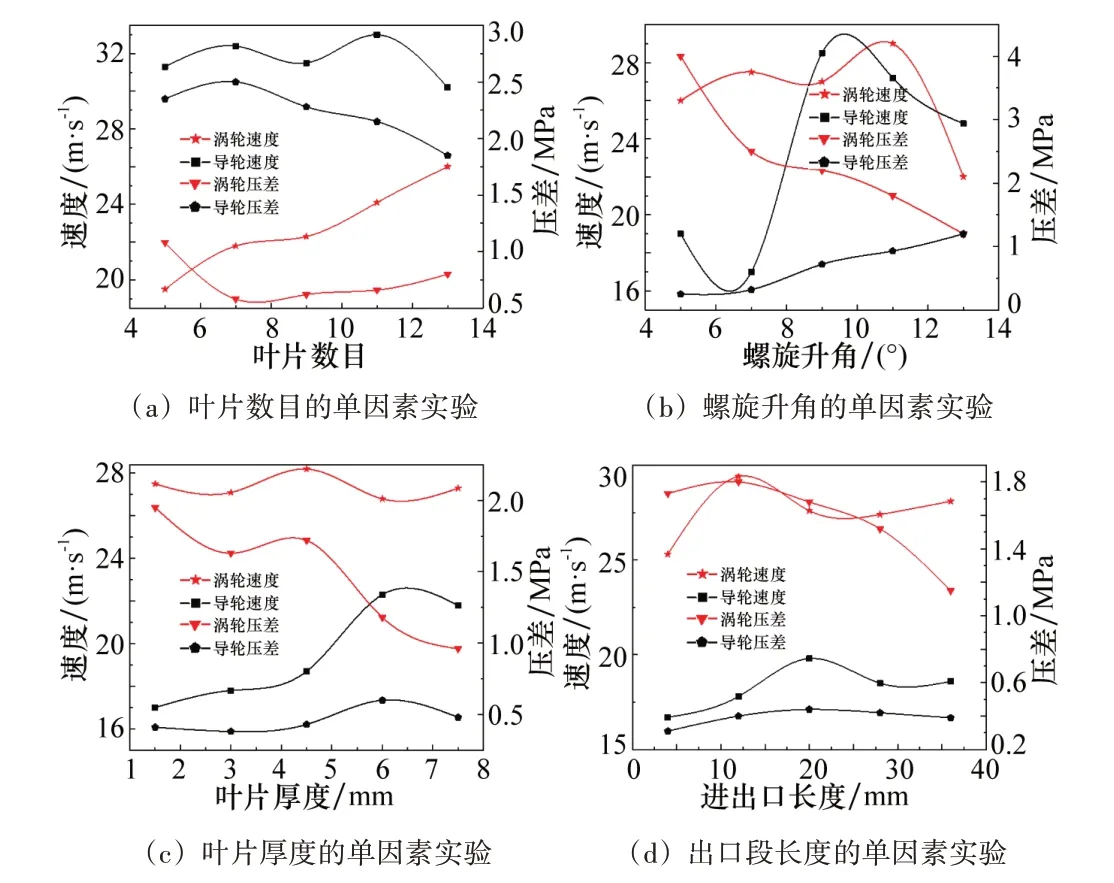
图4 涡导轮结构参数的单因素实验

如图4（c）所示，导轮速度在叶片厚度6 mm 附近压差有明显的波动，速度随着叶片厚度变化一直趋于平稳上升。涡轮压差随着叶片厚度增大而逐渐降低，在叶片厚度为4.5 mm 时，稍微有波动，特别是在叶片厚度为4.5 mm左右时，有明显变化。

如图4（d）所示，导轮速度在出口段长度为20 mm时有明显的波动，其中两者都在长度12 mm 处有微小波动，但变化效果并不明显。

3 响应曲面法参数匹配分析

响应曲面法[12]是一种统计学中的试验方法，针对某个单一因素进行取优运算，进一步由其实验结果得到拟合和优化后的模型。由第2 节的分析结果整理得到因素水平表如表2所示。

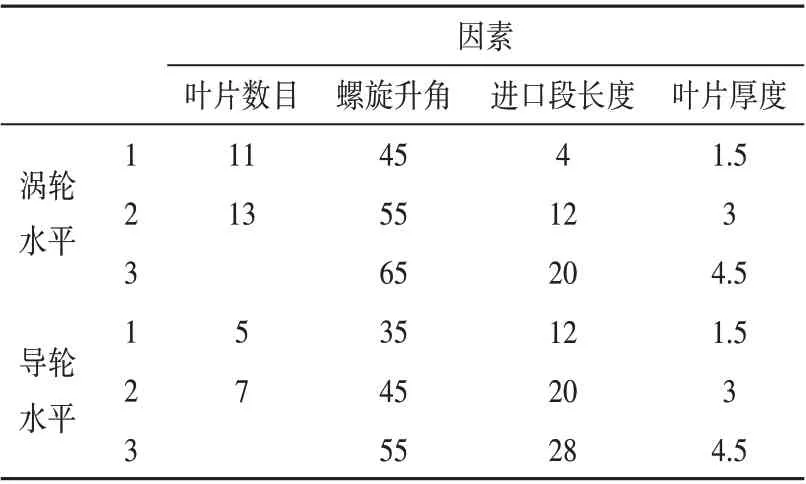
表2 因素水平表

3.1 响应曲面试验设计

响应曲面法是目前国际上较为流行的试验设计及数据分析方法[13]，依据涡导轮结构影响因素不同，对涡轮叶片结构选取显著性影响因素涡轮叶片数目Z1、涡轮螺旋升角β1、进口段长度L1、涡轮叶片厚度M1，对导轮叶片结构选取显著性影响因素导轮叶片数目Z2、导轮螺旋升角β2、出口段长度L2和导轮叶片厚度M2。

采用Box-Behnken 方法[14]对进行试验设计分析，由于分别有4个因素，其中包含3个连续因子和1个类别因子，每个因素有2或3个水平，若进行全面组合实验，则需要做54 次实验，两组需要做128 次实验，由于实验次数较多，所以采用响应曲面试验方法设计实验方案。响应曲面试验利用因素水平表安排较少次数实验。

本文利用Minitab 软件进行统计学分析运算与数据处理。在显著性水平0.05 的条件下，结合表2 因素水平表用Minitab 软件进行数据处理分析。基于Box-Behnken 得出结果，分析模型显著性时，多项评估值P值大于0.05[15]，表现为不显著。

由方差分析可知，涡轮在叶片厚度为4.5 mm 条件下，螺旋升角和出口段长度的影响最为明显。由图5 可知13 叶片下响应曲面图几乎一致，都在螺旋升角为55°附近达到峰值，从13 叶片的等高线图中可以明显看出选择出口段长度的影响几乎一样。

图5 轮的显著性结构参数响应结果

由方差分析可知，导轮在出口段长度为12 mm 条件下，螺旋升角和叶片厚度的影响最为明显。因此利用Minitab 得到其在不同叶片数目下交互作用的响应曲面图和等高线图，由图6可知在5叶片下响应曲面和等高线图几乎一致，5 叶片情况下效率明显较高，响应曲面图都在螺旋升角为55°附近达到峰值，等高线图的出口段长度都在3 mm附近达到峰值。

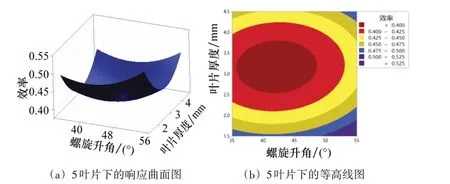
图6 导轮的显著性结构参数响应结果图

3.2 响应优化及结果验证

对上述参数进行响应优化得到优势方案并进行数值模拟，结果如表3～4 所示，可以直观地看到相对较优方案工作效率明显提高且与预测效率几乎相同，涡导轮效率明显得到了提高。

表4 导轮结果验证表

4 结束语

（1）利用数值计算软件模拟涡轮发电机的实际工况，响应曲面法得出的预测值进行对比，其各方案差值较小，表明响应曲面法应用于涡轮发电机结构参数优化具有可行性。

（2）随着相关参数的改变，速度和压差都有明显的变化趋势。

（3）经过验证，相对较优的参数组合效率明显提高。涡轮效率提高了0.2%，导轮效率提高了0.5%。优化结果较好，为井下涡轮发电机的实际生产提供了理论依据。