基于优化粒子群神经PID的双变量解耦控制

杨雨彬 任天宇 邓宏敬 蔡子龙 杨子墨

(东北大学秦皇岛分校控制工程学院 河北秦皇岛 066004)

在工业过程控制中，存在系统耦合现象，不但降低了控制精度，还降低了生产的品质和效率，其中双变量耦合现象较为常见。活塞往复式压缩机作为流程压缩机在国民经济支柱产业石油、化工行业有着广泛的应用。在压缩机气量调节系统中，气体需要连续的多级压缩将其提升到额定压后排出，在此过程中存在耦合关系，因此影响系统的控制品质，导致排气压力产生波动。该文针对往复式压缩机的双变量系统进行解耦控制，进而提升工业生产过程的控制质量。

PID 控制在控制领域中是最为传统、有效的控制方法，因为其结构简单、稳定性好等广泛应用于工业过程控制。其中PID的控制性能主要取决于比例、微分、积分系数的取值，系数的取值影响系统控制的动态性能、系统稳定性、超调量等众多方面。因此，PID 控制器参数选择至关重要，但是PID 控制器控制参数不易整定，应对复杂工况时效果不佳[1]，还需要引入智能算法进行优化。

粒子群优化算法（PSO算法）是一种基于群体协作的随机搜索算法，该算法参数设置少、收敛速度快、实现简单，常常应用于系统辨识，取得了较好的优化结果[2]。但是单一的粒子群算法容易陷入局部最优，导致误差较大。经过改进的粒子群算法既可以减少迭代次数，还可以提高算法精度及效率，常应用在焊接缺陷成因诊断、灰色预测模型改善等领域[3-4]，产生了较好的影响。

因此，该文针对二级往复式压缩机气量调节系统，利用PSO 优化算法和单神经元PID 控制的结合，实现在线调节控制器参数的效果，从而找到最优解耦效果。

1 单神经元PID

首先针对PID单一控制的缺陷，将神经网络与PID结合，构成单神经元PID。利用神经网络的在线学习能力，对网络连接权值和关键参数进行优化，实时调整控制过程中的比例、积分和微分系数大小，进而调整3个模块影响力的强弱。同时，当系统受到外界干扰时，单神经元可以及时调节PID 参数，保证参数快速回复稳定状态，从而提高控制系统的稳定性。

图1为单神经元PID 控制结构。w1、w2、w3为神经元连接权值，近似为PID 控制器的比例、积分、微分的问项的系数。通过对连接权值的调节，可实现PID控制参数的在线调整，改善了单一PID 控制时参数不易整定题。

图1 单神经元PID控制结构图

根据图示分析，其输出值如下：

式（1）中，K为神经元比例系数，K＞0。

其中连接权值的算法规则：

式（3）中，ηI为比例学习速率；ηP为积分学习速率；ηD为微分的学习速率。

经过实践表明，PID 参数的在线学习修正主要与e(k)和△e(k)有关，基于此，可将单神经元自适应PID控制算法中的加权系数学习修正部分进行。

采用改进后的算法后，权系数的在线修正变成了根据神经网络学习原理和实际经验相结合而制定。

通过对单个单神经元PID 控制进行分析，可以将其利用到多变量神经元PID 控制系统框图，如图2 所示。该文利用了双变量单神经元PID控制系统。

图2 多变量单神经元PID控制系统

2 PSO算法优化

2.1 PSO算法背景介绍

PSO算法是一种用于非线性函数优化的集群智能优化算法[5]，在解决大规模非线性问题中具有更高的优化效率和更好的优化结果。该算法在求解优化函数时，通过迭代寻优计算，能够迅速找到近似解，表现了较好的寻优能力；但是单一的PSO 算法容易陷入局部最优，导致结果误差较大。

近期粒子群改进策略主要体现在以下方面。

（1）PSO 算法的惯性权重模型，通过引入惯性权重，提高算法的全局搜索能力。

（2）带邻域操作的PSO模型，克服PSO模型再优化搜索后期迭代次数增加搜索。

（3）协同PSO算法，用K个相互独立的粒子群分别在搜索空间中不同维度方向进行搜索。

该文引入惯性权重，利用了自适应权重的PSO 算法，利用PSO 算法较强全局搜索能力[6-7]的优势，将神经元网络中权值的更新用PSO 中粒子的迭代来代替，得出网络初始权值和阈值最优解，进而实现对学习的优化及参数的最优选择。

2.2 自适应PSO算法优化

与原始PSO 算法相比，现在的惯性权重和迭代次数与每个粒子的适应度有关。引入了适应度概念，适应度越小，说明距离最优解跃进，需要局部搜索；适应度越大，说明距离最优解越远，需要全局搜索。

PSO 算法首先对粒子群初始化，随后粒子迭代更新“个体最优”值Pi、“种群最优”值Pg，迭代更新规律如下。

式（5）（6）中，m为粒子个数；d为空间维数；ω为惯性权重因子；c1为学习因子；rand()为(0,1)均匀随机数。

当达到最大迭代次数或粒子群搜索最优解时，迭代停止。其中，惯性权重因子ω大小影响算法的全局和局部搜索能力。因此，为了将全局和局部搜索能力最优结合，采用非线性的自适应权重因子调整方法，将ω值根据当前粒子适应度来调整，避免寻优过程中陷入局部最优，进而提高算法的全局收敛。

若f为粒子当前适应值，fmin为当前全部粒子适应值的最小值，favg为当前全部粒子适应值的平均值，则ω的取值满足

因此，通过控制惯性权重因子ω，可改进PSO算法的全局搜索能力，进而对算法达到优化。

3 仿真结果及分析

通过上述对控制方法及算法优化的分析，将其应用在双变量耦合系统中仿真研究。该文以压缩机气量系统进行仿真分析。

气量调节系统通过部分行程顶开进气阀的方式调节被压缩的气量而达到降低能耗的目的。气量调节系统通过部分行程顶开进气阀的方式调节被压缩的气体量而达到降低能耗的目的。经过查阅压缩机设计手册和对系统进行关联性分析可知，该系统存在较大的耦合性，一级和二级的设定值会对彼此产生影响。为验证本解耦方法的有效性，以二级往复式压缩机气量调节系统为研究对象，用MATLAB 和Simulink 相结合进行仿真研究，由槐斌等人[8]论述了可得气量调节系统的传递函数模型为

3.1 仿真流程

此次研究是以二级往复式压缩机气量调节为研究对象，使用单神经元PID 进行解耦控制，并通过自适应PSO 算法进行参数优化。图3 为整体框架结构模型。

图3 整体框架结构模型

其仿真寻优过程具体如下。

（1）在Simulink中搭建解耦模型，将控制对象的传递函数导入。构建S 函数，将PID 控制参数导入，进而确保3个状态变量初始值及PID的3个参数受控。

（2）自适应粒子群算法优化。

首先，对粒子群算法参数预设，通过经验及实践验证，将单神经元中3个状态变量和PID的3个参数进行上下界范围规范。3个状态变量范围为（0,1）；PID参数的比例系数为（900,1500）；PID 参数的积分系数为（0,2）；PID参数的微分系数为（-10,15）。通过优化缩小了算法寻优的范围，加快了寻优速率。根据其范围大小对粒子寻优的最大速度进行限制，确保寻优过程中寻优速度快且效率高。

其次，对粒子的位置和速度初始化。将初始值分别代入两组S 函数的3 个状态参量及PID 的比例、积分、微分系数。并运行Simulink的仿真模型，得到一组适应度值大小。在仿真中，将两组单神经元PID 控制回路的误差大小作为参考对象，对其绝对值进行实时积分，通过判断误差函数面积大小，来判断粒子寻优的效果。

最后，对局部适应度大小择优，不断进行迭代。通过迭代及局部适应度大小择优，在全部适应度进行寻优，实现全局适应度寻优。

通过PSO算法对参数的寻优及单神经元PID控制系统，进而实现对二级往复式压缩机气量调节系统的解耦。

3.2 仿真结果分析

通过粒子群算法的迭代寻优，得到以下两组适应度参数，具体数据见表1、表2。

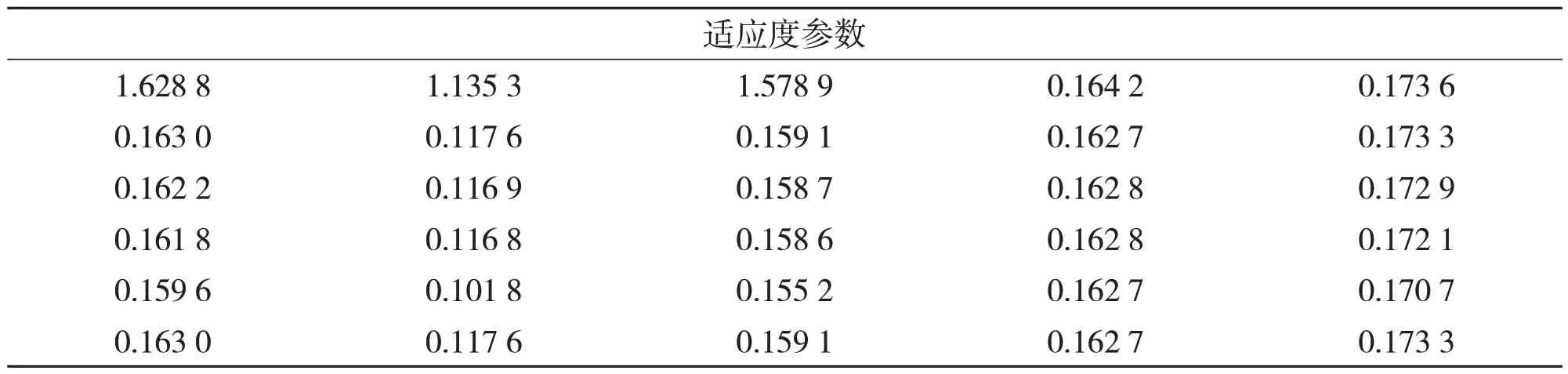
表1 第一组单神经元参数

表2 第二组单神经元参数

通过适应度变化可以发现，适应度经过参数寻优后有了不同程度的降低。在局部最优中的全局最优值降低了93.75%、39.90%。有较高的优化程度。

图4、图5 分别为优化后的误差仿真值，即适应度选取的参考依据变化。

图4 第一组误差仿真值

图5 第二组误差仿真值

通过图4、图5分析，可以发现在40 s时，变量趋于平行，基本无变化，适应度基本保持不变。因此选择适应度参数最小的优化系数为最佳。

此时，第一组单神经元PID 的3 个状态参数为0.921 5、0.292 4、0.954 9；PID的比例、积分、微分系数分别为1 024.3、0.212 5、0.503 2；第二组单神经元PID的3个状态参数为0.905 8、0.278 5、0.970 6；PID的比例、积分、微分系统系数分别为1 153.1、0.071 4、8.578 3。

同时，对两个结合的单神经元PID 解耦控制进行全局优化前后比对。

在仿真时，为了增加两组的解耦效果区分效果，将第一、二组脉冲值分别设为3、2。

通过图6、图7的观察比较，发现通过参数优化后，第二组变量的波动降低，且未出现在0 时刻的向下波动情况，有较好的稳定性效果。

图6 优化前解耦效果

图7 优化后解耦效果

因此，通过自适应PSO 算法优化参数的单神经元PID控制，解耦后的系统参数稳定效果提高，误差系数降低，具有较好的精确度。

4 结论

针对工业控制中的双变量系统耦合现象，该文探索了一种基于自适应粒子群算法优化的单神经PID解耦控制。该系统优势具体如下。

（1）具有较好的解耦性，将耦合系统分解为两个独立子系统，便于后期控制。（2）解耦控制稳定性提高，减少系统波动。（3）通过自适应粒子群算法寻优，将误差仿真系数大幅度降低，保证控制精度。（4）创新点：单神经元PID 与改进的自适应PSO 算法相结合，应用于双变量耦合系统中，提高解耦系统的稳定性。

该文针对双变量系统耦合现象，对系统进行仿真，其他双变量系统或多变量系统的应用需要进一步进行参数修改及改进研究。