Predicting and validating the load-settlement behavior of large-scale geosynthetic-reinforced soil abutments using hybrid intelligent modeling

Muhmmd Noumn Amjd Rj, Syed Tseer As Jffr, Aidhn Brdhn,Snjy Kumr Shukl

a Department of Civil Engineering, School of Engineering, University of Management and Technology, Lahore, Pakistan

b Department of Civil Engineering, National Institute of Technology (NIT) Patna, Patna, Bihar, 800005, India

c Geotechnical and Geoenvironmental Research Group, School of Engineering, Edith Cowan University, Joondalup, Perth, Australia

d Department of Civil Engineering, Delhi Technological University, Delhi, India

Keywords:Geosynthetic-reinforced soil (GRS)abutments Settlement estimation Predictive modeling Artificial intelligence (AI)Artificial neural network (ANN)-Harris hawks’ optimisation (HHO)

ABSTRACT Settlement prediction of geosynthetic-reinforced soil (GRS) abutments under service loading conditions is an arduous and challenging task for practicing geotechnical/civil engineers.Hence, in this paper, a novel hybrid artificial intelligence (AI)-based model was developed by the combination of artificial neural network (ANN) and Harris hawks’ optimisation (HHO), that is, ANN-HHO, to predict the settlement of the GRS abutments.Five other robust intelligent models such as support vector regression(SVR),Gaussian process regression (GPR), relevance vector machine (RVM), sequential minimal optimisation regression (SMOR), and least-median square regression (LMSR) were constructed and compared to the ANN-HHO model.The predictive strength,relalibility and robustness of the model were evaluated based on rigorous statistical testing, ranking criteria, multi-criteria approach, uncertainity analysis and sensitivity analysis(SA).Moreover,the predictive veracity of the model was also substantiated against several large-scale independent experimental studies on GRS abutments reported in the scientific literature.The acquired findings demonstrated that the ANN-HHO model predicted the settlement of GRS abutments with reasonable accuracy and yielded superior performance in comparison to counterpart models.Therefore, it becomes one of predictive tools employed by geotechnical/civil engineers in preliminary decision-making when investigating the in-service performance of GRS abutments.Finally, the model has been converted into a simple mathematical formulation for easy hand calculations, and it is proved cost-effective and less time-consuming in comparison to experimental tests and numerical simulations.

1.Introduction

In recent years, geosynthetic-reinforced soil (GRS) technology has grown in prominence as a means of constructing safe and sustainable structures such as GRS abutments.In comparison to the pile-supported abutment system (deep foundation), the GRS system is a more cost-effective and ecologically friendly method of supporting highway infrastructure and transportation projects(Abu-Hejleh et al.,2000;Zornberg et al.,2001;Phillips et al.,2016).

GRS is composed of closely packed granular fill material and geosynthetic reinforcing layers.Numerous experimental and numerical works have been carried out over the last three decades to evaluate the performance of GRS structures under static load conditions(e.g.Helwany,1993;Abu-Hejleh et al.,2000;Bathurst et al.,2000;Bueno et al.,2005;Hatami and Bathurst,2006;Adams et al.,2011; Ahmadi and Bezuijen, 2018; Zheng et al., 2018).All these studies showed that the geosynthetically reinforced structures offer high performance and excellent load-bearing capacity.

The GRS abutment is often used to support the bridge structure;therefore, determining its vertical settlement and lateral deformation is a vital serviceability requirement.Various methods are available in the literature to predict the lateral displacement of GRS abutments (Giroud, 1989; Jewell and Milligan, 1989; Christopher et al., 1990; Wu, 1994; Adams et al., 2002; Wu et al., 2013).The comparison,effectiveness,and applicability of these methods weredescribed in detail by Khosrojerdi et al.(2017).However, the estimation of vertical settlement of GRS abutments/walls requires further attention.Adams et al.(2011) provided an empirical relation for evaluating the settlement of GRS abutments/walls.The method was based on the assessment of the vertical strain of the GRS mass.Vertical strain in a GRS abutment is determined by intersecting the applied vertical stress owing to the dead load with the vertical strain envelope in the performance test stress-strain curve.Vertical settlement is then determined by multiplication of the calculated vertical strain with the abutment or wall’s height.Due to the emergence of powerful computing devices and major breakthroughs in artificial intelligence(AI),machine learning(ML)modeling techniques have made many traditional approaches outmoded.To date, no study has utilised AI/ML technology to predict the settlement of GRS abutments.Hence,there is a need to develop a method that can predict the settlement of the GRS abutments in an intelligent way with increased accuracy,bypassing all the aforehand assumptions and shortcomings often associated with traditional approaches.

In the past few years, the use of AI-based modeling techniques to solve complex engineering problems has garnered the interest of various scientists and researchers.AI is frequently utilised in a variety of engineering domains, including geotechnical engineering,to map the non-linear correlations between input and target variables(Zhang and Goh,2013,2016;Wang et al.,2020a,b;Atangana Njock et al.,2021;Kaloop et al.,2021;Tang and Na,2021;Wu et al.,2021; Zhang et al., 2021a, b, 2022; Bardhan et al., 2022).Many researchers have also successfully developed ML-based applications to investigate the behaviour of geosynthetic-reinforced foundation soil (Harikumar et al., 2016; Raja and Shukla, 2020, 2021a, b;Venkateswarlu et al., 2021).Unlike traditional approaches (empirical or analytical), AI models are predominantly data-driven, and hence, such models are not assumption bound.This ability of AI/ML-based models makes them extremely useful in acquiring knowledge from the underlying data in an intelligent way(Shahin et al., 2009; Raja et al., 2021).

Artificial neural network (ANN) is the most commonly and widely used ML-based method to predict the underlying behaviour of engineering systems.Its ability to learn the hidden relationship between the input and output variables, easy interpretation,handling multiple outputs,and effectiveness in predicting the new data have made it highly efficient among all the ML-based algorithms(Khan et al.,2022).However,recent studies have shown that metaheuristic-based optimisation techniques can boost the performance of ML-based methods (e.g.ANN) (Bardhan et al., 2021;Kardani et al., 2021).Such optimisation not only improves the predictive ability of the ANN but also helps in mitigating the common “local minima trap” problem by updating the learning parameters (weights and biases), thus yielding noteworthy results(Tien Bui et al.,2019;Zhang et al.,2020;Xie et al.,2021).This study utilises the newly developed Harris hawks optimisation (HHO).Accordingly,a novel hybrid model is developed by combining ANN and HHO, abbreviated as ANN-HHO, to predict the settlement of GRS abutments.The performance and reliability of the ANN-HHO have been established through comprehensive comparison with five other intelligent regression-based ML models including support vector regression (SVR), Gaussian process regression (GPR),relevance vector machine(RVM), sequential minimal optimisation regression (SMOR), and least-median square regression (LMSR).Rigorous statistical analysis, including traditional and modern performance evaluation indicators, ranking criteria, and multicriteria approaches, has been employed to ascertain the accuracy of the developed ANN-HHO model.The generalisation ability and trustworthiness of the ANN-HHO model have been assessed through uncertainty and sensitivity analysis (SA).The model was also substantiated by comparing the results of several large-scale independent experimental studies on GRS abutments as reported in the scientific literature with the ANN-HHO’s results.Most importantly, the model is converted into a mathematical formula for easy implementation.It is proved helpful for practitioners in estimating the settlement of GRS abutments.

2.Methodological background

This section describes the methodological background of the hybrid intelligent paradigm developed in this study(i.e.ANN-HHO)to predict the settlement of GRS abutments.Moreover, it also includes the brief outlook of other methods such as SVR, GPR, RVM,SMOR, and LMSR, developed for predicting the settlement of GRS abutments.

2.1.ANN

ANN imitates the human nervous system and consists of a highly interconnected set of processing elements called neurons.An ANN architecture comprises a three-layered system, that is, an input layer, hidden layer(s), and an output layer.In each layer, the neurons are logically arranged and interact through weighted connections (Shahin et al., 2001).In order to solve complex problems,data are presented to the model network via the input layer.Afterward,the data are processed in the hidden layer(s),and passed through the output layer.During the entire process,the interaction between the network layers is done through the neurons.The output of each layer is produced by multiplying the input of the predecessor layer with the weight connections.After adding the weighted inputs to the bias (threshold), the transfer function is applied to obtain the neuron’s output.Fig.1 represents the general structure of the ANN utilised in this study.For the historical development and detailed description of the ANN,readers can refer to any of the excellent ML works available in the literature (e.g.Russell and Peter, 2010; Aggarwal, 2018).

2.2.HHO

Harris hawk is a swarm-based optimisation technique recently developed by Heidari et al.(2019).Originally inspired by the predatory behaviour of the Harris hawks,this intelligent techniqueis effectively applied in solving and optimising many scientific problems (e.g.Yıldız and Yıldız, 2019; Jiao et al., 2020; Bardhan et al., 2021).The main advantage of HHO is its gradient-free optimisation approach;thus,it can be used for constrained engineering problems in an efficient way(Heidari et al.,2019).Fig.2 shows the different phases of the HHO.

Fig.1.Typical architecture of ANN.

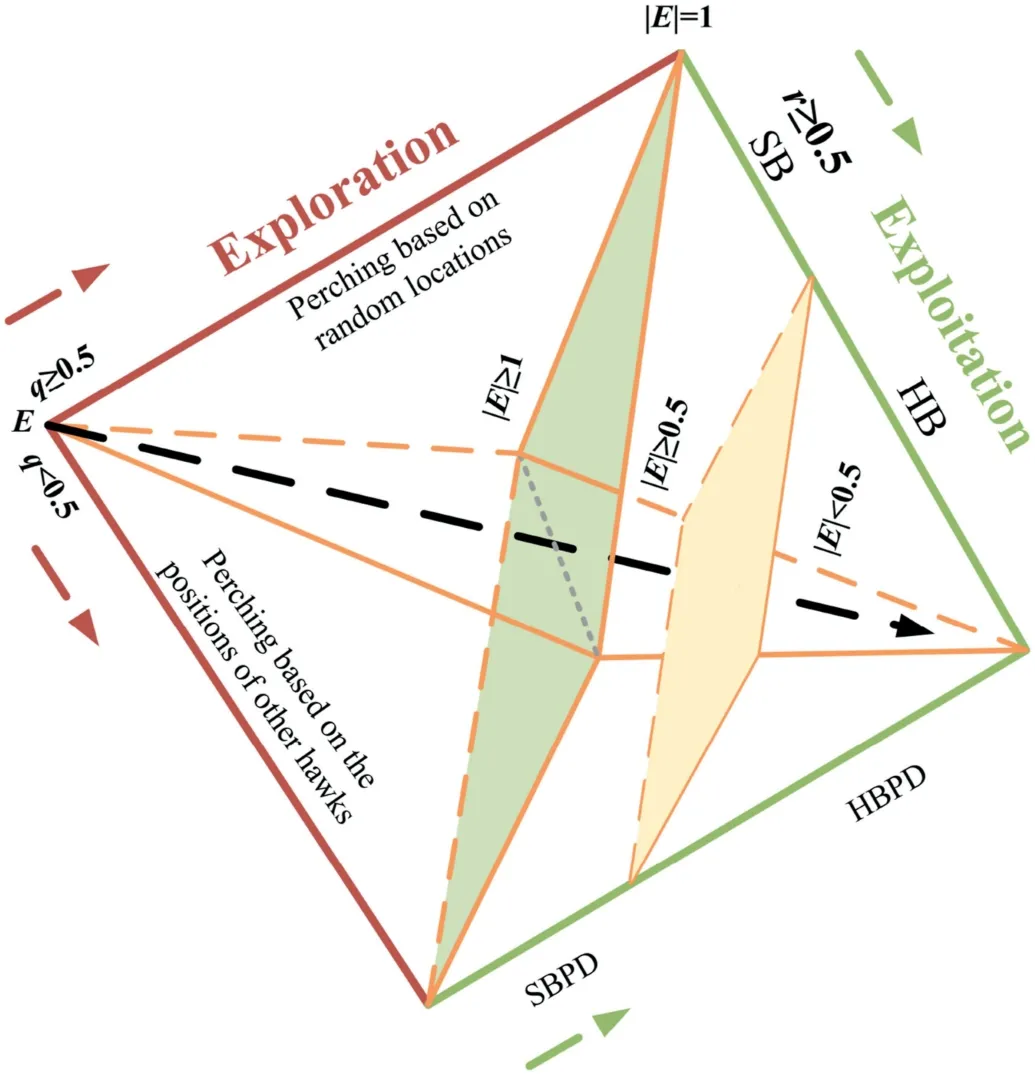
Fig.2.Different phases of HHO (adapted from Heidari et al., 2019).

The first phase of the HHO is exploration.Harris hawks are natural predators that can detect and track prey using their extremely powerful eyesight.In mathematical terms, the Harris hawks are candidate solutions, and the intended prey is deemed the best candidate(optimum)in each iteration.In HHO,the Harris hawks work in groups and pounce (strike) on prey from various locations.The hawks employ several chasing strategies and tactics according to different scenarios,and prey’s escape strategies.When the best hawk tracks the prey and comes within striking distance,the prey escapes while the other hawks keep on chasing the prey.This strategy will leave the prey exhausted and defenseless,making it easily hunted.Mathematically, this exploration phase is defined as follows (Heidari et al., 2019):

where xrand（t） is the randomly selected hawk from the current population; x（t） is the hawk’s location at the current step (iteration);x（t+1）is the hawk’s location at the forthcoming step;xprey（t）is the prey’s location; r1, r2, r3, and r4are the random numbers ranging from 0 to 1 and updated in each step; Uband Lbare the upper and lower bounds of variables, respectively; qprepresents the perching strategy depending on either the location of other hawks in the population(closeness to the prey when attacking)and is modeled as qp＜0.5 in Eq.(1), or perch on tall trees (random location within the search area range) modeled as qp≥ 0.5 in Eq.(1);and xmis the mean(average)position of the hawks(within the current population) and is given as

Fig.3.Pseudocode of HHO (Heidari et al., 2019).

where xi（t）and nhrepresent the location of each hawk at step t and the total population of hawks, respectively.

The second phase is the transition phase between exploration and exploitation,which deals with the escaping energy of the prey.As the prey continuously tries to escape,it will keep losing energy,and this energy loss E is modeled as follows:

where Eois the initial state of the prey’s energy and changes randomly inside （-1，1） for each step t, and T is the maximum number of steps.It is essential to understand that the algorithm is designed to replicate the natural behaviour of hawks and their prey.The dynamic energy of the prey has a decreasing trend, which implies that exploration will occur if |E| ≥1 and exploitation will occur if |E|＜1 (Heidari et al., 2019).

The third phase of the HHO is exploitation, during which the Harris hawk hits the prey discovered in the preceding phase.While the hawk is attacking, the prey attempts to flee the dangerous position.The prey and hawk’s evading and chasing behaviours result in four different techniques during the attacking phase of HHO: soft besiege (SB), hard besiege (HB), soft besiege with progressive rapid dives (SBPD), and hard besiege with progressive rapid dives (HBPD).The theoretical details and mathematical formulations of these strategies can be found in the literature(Heidari et al., 2019).According to the probability of prey escaping successfully (r ＜0.5) or unsuccessfully (r ≥0.5) prior to the surprise attack, the following tactics were inferred based on the prey’s escaping energy:

Fig.4.Proposed research framework for hybrid ANN-HHO paradigm developed in this study.

The pseudocode of the HHO is given in Fig.3.

2.3.Hybridising of ANN-HHO

As discussed earlier, the major drawback of ANN is the local minima trap, and the metaheuristics-based optimisation techniques help in overcoming this problem.Therefore, the hybridisation helps to evade the local minima issue and significantly enhances the predictive ability of the ANN.

After dividing the dataset into training and testing sets, the first stage of the hybridisation process is to initialise the ANN,which involves the generation of weights and biases.The ANN’s ideal structure(hidden layers and nodes)is determined using a hit and trail process.Thereafter,the weights and biases were optimised through HHO,and the model was validated through the optimised HHO’s weights and biases.It may be noted that the mutation-based strategy proposed by Kardani et al.(2021) has been utilised to further improve the performance of HHO.For this,the position of each prey in HHO has been updated by creating a diversified solution space for each step(iteration) by utilising the velocity approach of the particle swarm algorithm(PSO),which can be mathematically expressed as

where vmand wmare the mutant’s velocity and inertia weight,respectively.The mutant velocity is updated in each iteration according to Eq.(8).This updated velocity is then used to update the best prey’s location as follows:

If the new location’s fitness is greater than the prey’s existing location fitness,this new location will be identified as a prospective location.To find the optimum location of the prey, the mutation algorithm will keep boosting the location by comparing the present and potential new locations in each iterative step.The research framework applied for developing ANN-HHO in this study is presented in Fig.4.

2.4.SVR

SVR is developed by Drucker et al.(1997) and is based on the structural risk minimisation principle.It converts the input data to the higher-dimensional feature space using a non-linear transfer function.Therefore, if X is the input variable and Y is the target variable (settlement of GRS abutments in the present study), SVR can be written as follows (Smola and Schölkopf, 2004):

where w is the weight vector, φ represents the mapping function for feature extraction, and bsvris the bias term.Based on the Mercer’s theorem, the SVR utilises the kernel function to perform the linear separation (Vapnik, 1999).Mathematically, it is defined as follows:

where λ is the Lagrange multiplier,and K is the kernel function.For detailed mathematical derivation of SVR,readers may refer to some excellent studies(Drucker et al.,1997;Smola and Schölkopf,2004).The kernel functions such as linear, sigmoid, polynomial, and radial bias kernel are available.For this study, radial bias kernel(RBF) function is used to obtain the optimal results.The mathematical formulation of RBF is given as

where ‖x-x＇‖2is the square of Euclidian distance between the training and testing patterns, and σ is the Pearson’s kernel width.

2.5.GPR

For comparing the results of ANN-HHO, the computationally intelligent GPR model has also been developed and implemented.It has been successfully applied in many scientific problems for prediction purposes(Gao et al.,2019;Khan et al.,2021).GPR is a nonparametric methodology based on Bayesian theory that utilises the principle of information sharing across neighbouring data to forecast the target variables.Mathematically, it can be expressed as

where μ（y） and k（y，yi） are the GPR mean function and covariance kernel function.The optimum results in this study are obtained by utilising the Pearson’s VII universal kernel(PUK) function:

where ϖ is the peak tailing factor.For more details regarding the GPR model, and mathematical implications in the field of ML,readers can refer to some excellent books (e.g.Rasmussen, 2004).

2.6.RVM

Based on sparse Bayesian inference, RVM is a supervised ML technique that obtains closed-form solutions to regression problems.RVM is a specialised version of the sparse kernel model first presented by Tipping (2001) and has a mathematical structure comparable to that of support vector machine(SVM).In contrast to SVM, RVM evades the parametrisation issue, which is usually associated with SVM and often requires a cross-validation approach.The mathematical form of RVM is similar to that of SVR(Eq.(10) and (11)); however, the kernel function in RVM does not require satisfying Mercer’s theorem (Tzikas et al., 2006).More details about the historical development of RVM can be found in the literature (Tipping, 2001).

2.7.SMOR

Originally introduced by Platt (1998), SMOR is an extended version of minimal sequential optimisation(SMO).During SMO,the critical ridge is defined by the maximum amount of the error between the original and predicted values (maximum error deviation).If the estimated error is greater than the maximum error deviation (∂), then it can adversely affect the performance of the system; otherwise if it is less than ∂, then it can be neglected.A large quadratic programming (QP) optimisation problem needs to be solved when training the SVM.The SMO decomposes this large QP problem into several smaller QP problems.Thereafter,small QP problems can be solved using analytical techniques, thus minimising time and memory consumption for the training dataset.For this study,RBF kernel function and an improved learning algorithm by Shevade et al.(2000) have been employed for implementing SMOR.

2.8.LMSR

LMSR is a semi-parametric, non-linear quantile regression method that yields better results than linear regression (LR).The main difference between the LMSR and LR is that the former uses the median of error as the measure of central tendency while the latter employs the mean value of errors(Rousseeuw,1984).Unlike the LR,the LMSR is not sensitive to outliers.In a general LR problem,the residuals can be defined as follows:

where rkis the residual,okis the output,xkis the input value for the kth variable, and c and c＇are the regression coefficients.This technique aims at reducing the median of error as follows:

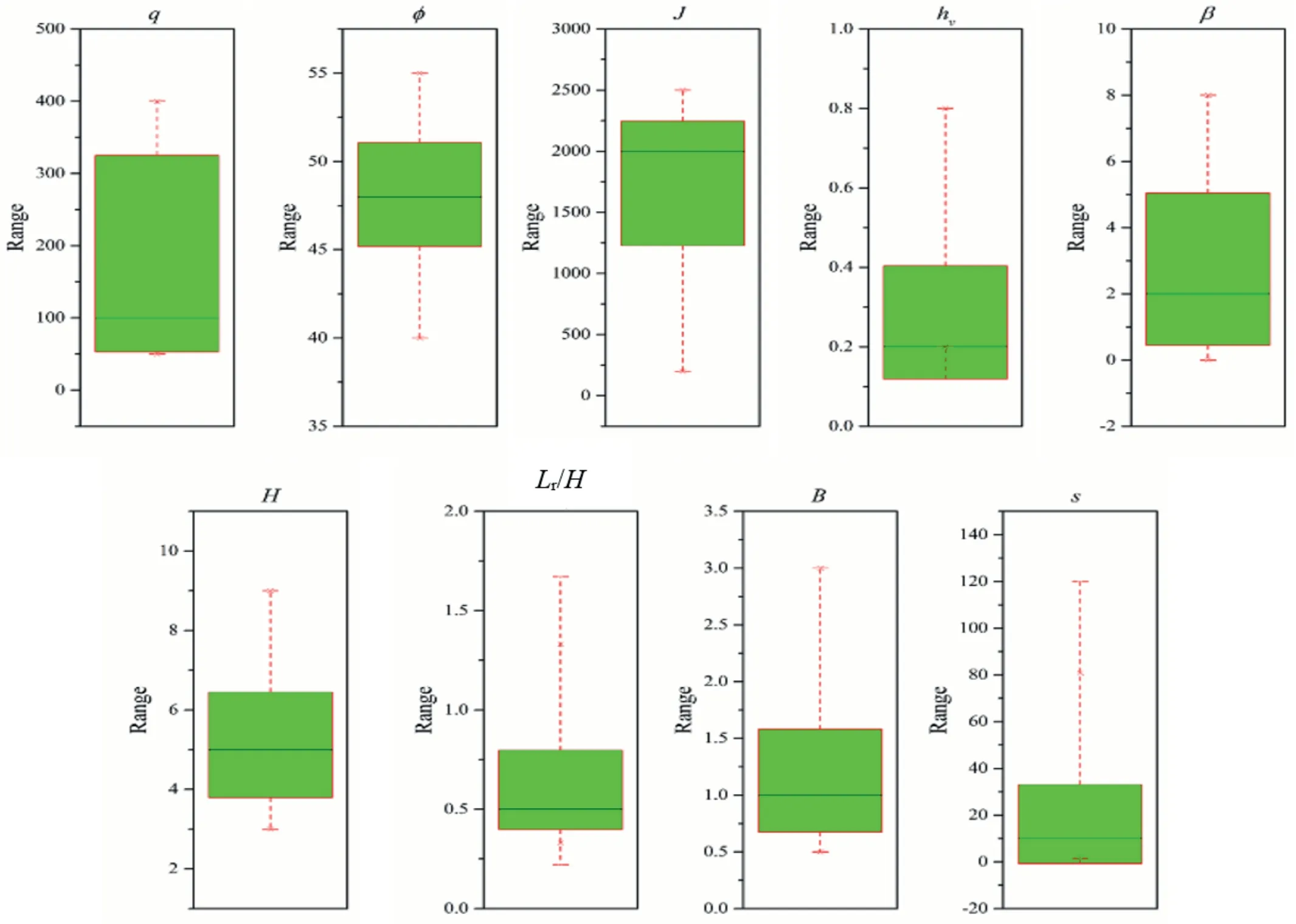
Fig.5.Box and Whisker plots of GRS abutment settlement database.

2.9.Database development and preprocessing

In this study, 354 data points reported by Khosrojerdi et al.(2020) have been collected to generate the primary dataset.The data are generated through a finite difference modeling (FDM)based parametric study performed by validating the full-scale tests on GRS walls by Bathurst et al.(2000).Four walls (1, 2, 3, and 4)were constructed by Bathurst et al.(2000) for their full-scale testing.All the walls had the height of 3.6 m and the same constructing units (modular concrete blocks).The geometric configuration of the first two walls (1 and 2) was identical, with the only difference in strength and the tensile modulus of geosynthetic.For the third wall,four reinforcement layers were placed with a spacing ratio of 0.9.The fourth wall was constructed without the hard face,and geosynthetic layers were arranged in the wrapped form.The soil properties, reinforcement characteristics, and GRS wall parameters used in the original study are summarised in Table 1.Khosrojerdi et al.(2020) simulated the first two walls for conducting the parametric study using the FDM based suite (FLAC3D).For simulating the soil’s non-linear behaviour,the plastic hardening model originally proposed by Schanz et al.(1999) was utilised in their study.For predicting the maximum settlement(s) of GRS abutments, the most critical attributes considered were: applied/service load (q), angle of internal friction of soil (φ), abutment height(H),facing batter angle(β),the width of concrete footing(B),reinforcement spacing (hv), length-ratio of reinforcement (Lr/H),and initial tensile modulus of reinforcement (J).Figs.5 and 6 represent the box and whisker plot and correlation matrix of the complete dataset utilised to build the ANN-HHO model, respectively.The detailed statistical properties of the dataset are summarised in Table 2.

Table 1Material and wall properties in Bathurst et al.(2000).

3.Model development and implementation

This section describes the development and implementation of the AI models constructed in this study.For model development,the first step is the data division into training and testing datasets.Training dataset is used to train the models, and testing dataset is used to validate them.For this study, 75% of the dataset has been randomly earmarked for training and another 25% for testing.It is worth noting that the testing dataset plays no part in the training phase of the models.

3.1.ANN-HHO

The first step is the determination of ANN optimum architecture, i.e.number of hidden layer(s), number of hidden nodes(neurons), training algorithm and transfer function.Hornik et al.(1989) showed that, given adequate weight connections, a single hidden layer can approximate the function with sufficient accuracy.Due to its fast convergence rate and excellent performance in previous studies, Levenberg-Marquardt back propagation is usedas the training algorithm (Alsmadi et al., 2009).Based on the gradient decent approach, this algorithm tries to diminish the network’s error by moving down the gradient of the error curve.

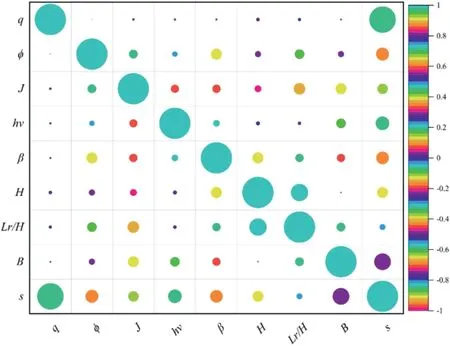
Fig.6.Correlation matrix of the input variables.

The MATLAB environment has been utilised for developing the ANN-HHO model to predict the settlement of GRS abutments.The framework for predicting the settlement of GRS abutments is already given in Fig.4.

To avoid the scale issues, data should be normalised before feeding it to the model network.Therefore,in this work,the whole dataset has been normalised in [-1, 1] using min-max scaling method as follows:

where x＇is the normalised value of the variables;and xminand xmaxare the minimum and maximum values, respectively.

As stated earlier,the hit and trail procedure is used to establish the optimum network structure.The architecture of an optimum ANN is 8-4-1 with a single hidden layer having 8 input parameters,4 hidden neurons, and one output.Also, the tangent-sigmoid activation function as given in Eq.(18) is employed in the hidden layer, and its range is from -1 to 1.It is worth noting that the tangent-sigmoid function has been predominantly applied in many previous ANN-related studies (Ghorbani et al., 2020; Raja and Shukla, 2021a):

Following the selection of the optimal ANN topology, HHO was used to optimise the ANN’s weights and biases for determining the settlement of GRS abutments.To train the neural network, the optimisation approach of Shahin et al.(2001) was used to determine the optimal number of hidden layer nodes.This was accomplished by increasing the number of hidden layer nodes throughout the model’s training phase until no additional improvement over the testing dataset was obtained.It is noteworthy that this improvement is characterised by the decrease in root mean square error (RMSE) values.Once the optimal number of hidden nodes is decided(i.e.4 in this study),the corresponding weights and biases of ANN are fed to the HHO model.

In HHO, again RMSE is exploited as a cost/fitness function for any number of iterations.The search process was conducted in iterations(t=100-500) and Harris hawk population(nh=10-30).As mutation-based strategy is used to further improve the performance of HHO, the inertia weight (wm) was varied from 0.4 to 0.9(Kardani et al.,2021).Finally,the optimal model with deterministic factors are obtained after the hit and trail procedure run, and are summarised in Table 3.Fig.7 shows the convergence curves (iterative performance) of ANN-HHO model in training and testing datasets.The final structure of the optimum ANN-HHO model network is illustrated in Fig.8.

3.2.Other AI models

All other AI models such as SVR, GPR, RVM, SMOR and LMSR were developed and implemented according to the procedure described in Section 2.It is important to note that the same training and testing datasets have been used for developing these models.The hyperparameters of all the models are summarised in Table 4.

Table 2Detail descriptive statistics of complete dataset.

4.Results and discussion

4.1.Model performance and evaluation

Six statistical indices were computed to analyse and compare the developed models’accuracy.This includes:(i)the coefficient of determination (R2), (ii) the RMSE, (iii) the scatter index (SCI), (iv)the mean absolute error (MAE), (v) the mean arctangent absolute percent error (MAAPE), and (vi) the Nash-Sutcliffe coefficient

Note: SE = Standard error; SD = Standard deviation.(NSC).All of these statistical indices are widely used to determine the accuracy of ML-based models(Gao et al.,2019;Raja and Shukla,2021a).However, new research indicates that the predictive strength of ML-based models should not be determined solely by individual evaluators(Naser and Alavi,2021).As a result,the multicriteria approach is also used to evaluate the model’s reliability and trustworthiness (Gandomi et al., 2013; Golbraikh et al., 2003).Table 5 summarises the mathematical formulations of all statistical indices.The R2and NSC values of unity and the RMSE,MAE,SCI,and MAAPE values of zero indicate an ideal model.The study discusses the multi-criteria method in greater detail later in the paper.

Table 3Parameters of ANN-HHO model.

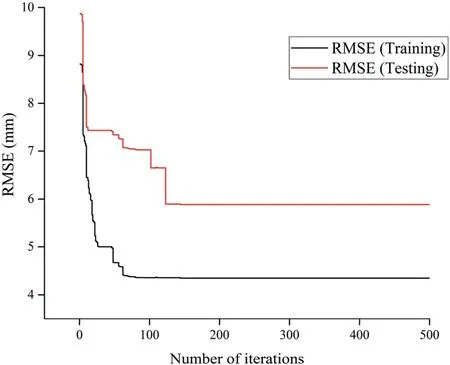
Fig.7.Iterative performance of ANN-HHO in training and testing datasets.

The performance of all the developed models is illustrated using the ranking technique (RT).For this, each model is ranked according to the strength of the utilised statistical indices indicated in Table 5.A higher precision level(i.e.large R2and NSC,and lower RMSE, SCI, MAE, and MAAPE) gives the highest rank(according to the number of indices used,i.e.6)and vice versa.The results of the statistical evaluators (R2, RMSE, SCI, MAE, MAAPE, and NSC) for ANN-HHO, SVR, GPR, RVM, SMOR, and LMSR in the training and testing datasets are summarised in Tables 6 and 7, respectively.After examining both the datasets,it can be observed that the ANNHHO has achieved the highest score (i.e.36 in both datasets, and the total score = 72).The second and third best performances are shown by the GPR and SVR models, with scores of 30 and 24 for both the training and testing datasets, thereby achieving a total score of 60 and 48,respectively.The RVM,SMOR,and LMSR models have shown poor predictive strength with scores of 14,13,and 9 in both datasets and the total scores of 28, 26, and 18, respectively.

Finally, the overall prognostic veracity of all the data-driven paradigms is depicted in Fig.9 via Taylor’s diagram (Taylor, 2001).In terms of settlement prediction of GRS abutments, this figure represents the accuracy of the developed models considering SD,correlation coefficient(R),and centred RMSE in testing dataset.The ideal model in a simulated field is indicated by the measured SD(16.87 mm), R of unity, and centred RMSE of 0.Regarding the diagram,it can be perceived that for the ANN-HHO model, SD,R, and centred RMSE have values of 17.93 mm, 0.964, and 4.77 mm,respectively.This revealed an excellent overall prediction (close to the measured values)for the developed ANN-HHO model.For SVR,GPR, RVM, SMOR, and LMSR, the values of SD, R, and RMSE were(10.74 mm, 0.907, and 8.44 mm), (12.67 mm, 0.95, and 5.92 mm),(15.91 mm,0.847, and 9.09 mm),(9.31 mm,0.821,and 10.62 mm),and(8.33 mm,0.8,and 11.34 mm),respectively.This showed that in comparison to ANN-HHO, all these models are associated with more bias in estimating the settlement of GRS abutments.Hence,at this point, it can be concluded that the hybrid ANN-HHO can predict the GRS settlement values in an intelligent and reliable way.

4.2.Multi-criteria approach

All the above-mentioned indices are well-recognised for statistical analysis.However,the latest research has shown that the AI/ML models should not solely be judged based on individual evaluators (Naser and Alavi, 2021).Despite the well-established credibility of these indices, they are still associated with certain biases and, therefore, can undermine or give false hype to the predictive ability of the models.Therefore, a multi-criteria approach is also used to ascertain the accuracy of the models.For this,OBJ function and external validation analysis were conducted (Golbraikh et al.,2003; Gandomi et al.,2013).The OBJ function is given as follows:

where Notrand Notsare the total numbers of training and testing datasets, respectively.The lower the value of OBJ function, the higher the accuracy of the model,and vice versa.The OBJ values of all the prescient models are depicted in Fig.10.It displayed that the ANN-HHO model has the lowest OBJ value (6.53), thus having the highest accuracy, followed by GPR (8.32) and SVR(9.97).

An external validation criterion developed by Golbraikh et al.(2003) is also used to determine the forecasting ability of the models.This criteria evokes more penalties on the models through more rigorous statistical analysis,thus ensuring their reliability and trustworthiness rather than coincidental closeness between theactual and predicted values.This following criterion should be satisfied.Between the observed and predicted values,or vice versa,one of the slope regression lines (K or K＇) must pass through the origin and be near to 1.For settlement prediction of GRS abutments,it can be represented as follows:

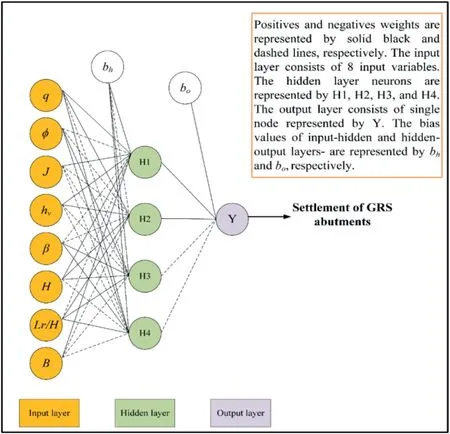
Fig.8.The optimum ANN-HHO structure (8-4-1).

The K orK＇must be between 0.85 and 1.15.Additionally, the coefficient of determination passing through the origin should be less than 0.1.Hence,performance indices(m＇and n＇)should be less than 0.1 and can be estimated as follows:

where R2oand R＇2oare the regression coefficients and can be estimated as

Ideally, the values of R2oand R＇2oshould be close to measured coefficient of determination (R2), whereas R2should be greater than 0.6.Roy and Roy (2008) extended the external validation criteria by introducing a fourth condition, that is, model stabilisation criteria (Rs).Mathematically, Rsis calculated as

In this manner,a model is deemed acceptable if it satisfies all of these criteria.Table 8 summarises the findings of the external validation criteria.The results indicate that the ANN-HHO and GPR models show good prediction ability for evaluating the settlement of GRS abutments.This is supported by the fact that these two models satisfy all four of the external validation approach’s underlying requirements.However, the ANN-HHO model did better than the other models when ranking criteria based on the performance of standalone statistical indices, the OBJ function, and an external validation method were combined.

Table 4Hyperparameters of SVR,GPR, RVM, SMOR,and LMSR models.

Table 5Statistical indices and their mathematical euqtaions.

Table 6Performance ranking of all the models in the training dataset.

Table 7Performance ranking of all the models in the testing dataset.

Table 8Results of external model evaluation criteria.

4.3.Uncertainty analysis

In this sub-section, all the developed models for settlement prediction of GRS abutments are quantitatively assessed via uncertainty analysis.For this, the complete dataset of 354 observations(training and testing)was used to assess the reliability of the predictive models.It is irrefutable that the settlement predictions made by the AI models (ANN-HHO, SVR, RVM, SMOR, and LMSR)are associated with uncertainties (e.g.uncertainty in input variables, model parameters, numerical simulations, etc.).Therefore,the uncertainty analysis can be used for the logical comparison of predictive ability of all the models.For uncertainty analysis.The following parameters needed to be calculated:(i)absolute error(ε);(ii) average of errors (AOE,）; (iii) SD; (iv) margin of error (MOE);and(v)width of confidence interval band(WCIB).In this study,the confidence interval of 95%was used,representing the error range in which approximately 95%of the data are located.The mathematical formulation of these parameters is given below:

Fig.9.Visualisation of predictive accuracy of all the models via Taylor’s diagram.

Fig.10.OBJ function values of all the AI models.

where n is the length of the data,i.e.number of points;and UB and LB represent the upper and lower bounds of the confidence interval,respectively.The performances of all the models are illustrated in the form of bar plots(see Fig.11).It is noteworthy that the lower value of WCIB provides more accurate predictions of the model.In other words,a model showing a lower value of WCIB is associated with less bias, and predictions made by it will be much more reliable than those showing a higher value.The ANN-HHO model has shown lower values of WCIB (1.67) and MOE(0.83) in comparison to its counterparts and is the most accurate model.Also,the values of AOE (2.23) and SD (4.01) for the ANN-HHO model represent higher trustworthiness in comparison to other models developed in this study.

4.4.Performance assessment of the models via probability distribution

The ability of the developed ANN-HHO model to emulate the probability distribution of the measured GRS settlement data was visually assessed via violin plots.The plots of observed versus AI model-simulated settlement are illustrated in Fig.12.The similarity between the models is represented by the distribution of the predicted (simulated) and observed GRS abutment settlement data.From Fig.12,it can be observed that the simulated settlement data of ANN-HHO model are close to the observed settlement data.The next best similarity can be observed for the GPR model.The highest distortion in the violin was observed for the LMSR model followed by the SMOR model.Consistency in the results shows a clear preeminence of the ANN-HHO model in simulating GRS abutment settlement.

4.5.Model robustness and SA

In the development of ML-based applications for prediction purposes, SA and feature importance analysis are imperative to estimate the strength of input variables on the output of the model(Wang et al., 2020a; Zhang et al., 2021b).A good and dependable model is one that fits the calibration data well and also predicts the studied system’s underlying physical behaviour rationally (Shahin et al., 2009; Raja and Shukla, 2021a).The SA was performed in this section to determine the ANN-HHO model’s robustness,and to assess the strength of the input parameters(q,φ,J,β,hv,H,Lr/H,and B) on the settlement of GRS abutments.

Shahin et al.(2009)proposed the SA technique to determine the derived model’s generalisability.For this, one input parameter is increased from the lowest to the greatest value(within the training data range), while the remaining parameters are held constant at their mean values,and the associated output is assessed.This is also referred to as a one-at-a-time(OAT)SA.Twenty equal incremental steps were chosen for this study in order to examine the effect of each parameter on the settlement of GRS abutments.At each stage,the following normalised value of the Sensitivity index (SI) is calculated (Hamby,1995):

where sp（t）and sp（i+1）are the predicted GRS abutment settlements at steps i and i+1,respectively;and x（i）and x（i+1）are the values of variable at steps i and i +1, respectively.

Fig.13 illustrates the findings of the SA.The positive number indicates that the GRS settlement increases when the associated parameters increase, while the negative value indicates that the GRS settlement decreases as the corresponding parameters increase.The increases inthe applied load,reinforcementverticalspacing,heightof the abutment, and width of footing resulted in the increase in the settlement value.On the contrary, increases in the friction angle,tensile stiffness,facing batter angle,and length-ratioof reinforcement caused the decrease in the settlement of GRS abutments.Similar results were found in the earlier studies (Wu, 2006; Wu et al., 2006;Khosrojerdi et al., 2020).Therefore, it can be established that thedeveloped ANN-HHO model has good generalisation ability, and predicts the settlementof GRSabutments inaway thatcoincides with the underlying general physical behaviour of the investigated system.

Fig.11.Result (bar chart) of uncertainty analysis.

4.6.Evaluation of ANN-HHO through independent case studies

To assess the proposed ANN-HHO model’s accuracy in predicting the settlement of GRS abutments,three large-scale experiments described in the scientific literature were chosen to compare measured and anticipated settlement values.The parameters used in the studies of Helwany et al.(2007),Wu et al.(2008),and Hatami and Doger (2021) are summarised in Table 9.The measured settlements of GRS abutments obtained in these studies have been compared with the predicted values by ANN-HHO, and are presented in Fig.14a-d.The results were also compared with the Adams et al.(2011)’s empirical method.From the results, it can be concurred that the developed ANN-HHO model predicted the settlement with fair accuracy, and has outperformed the traditional empirical method.This can be confirmed with the estimated values of MAE.In the studies of Helwany et al.(2007),Hatami and Doger(2021), and Wu et al.(2008), the obtained MAE values are 17.4(dataset 1)and 15.3(dataset 2),5.3,and 13.12,respectively,for the ANN-HHO model; wheareas for the same datasets, the values are 34.9 (dataset 1) and 66.9 (dataset 2), 7.6, and 37.32, respectively,obtained by the method of Adams et al.(2011).It should be noted that this comparison is based on relatively small datasets,thus the results cannot be generalized as superiority of one model over another.

Table 9Input parameters of GRS abutments for independent case studies.

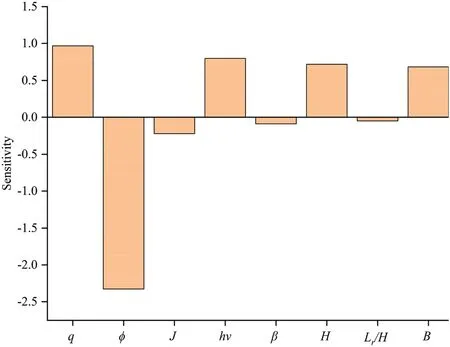
Fig.13.SA for evaluating the robustness and generalisation ability of the ANN-HHO model.

To this point, the accuracy, reliability, and robustness of the ANN-HHO model have been assessed via rigorous statistical analysis, ranking criteria, multi-criteria approach, uncertainty analysis and SA, and independent validation from field-scale studies.However,in order to convert the developed ANN-HHO model from“black-box” to “glass-box”, it is imperative to convert the model into a mathematical formulation.Such a mathematical formulation will help the practitioners estimate the settlement of the GRS abutments with ease.Moreover, it will allow the researchers to track,build,improve,or criticise the developed model.Therefore,in the next section, the model is converted into a simple trackable formula.

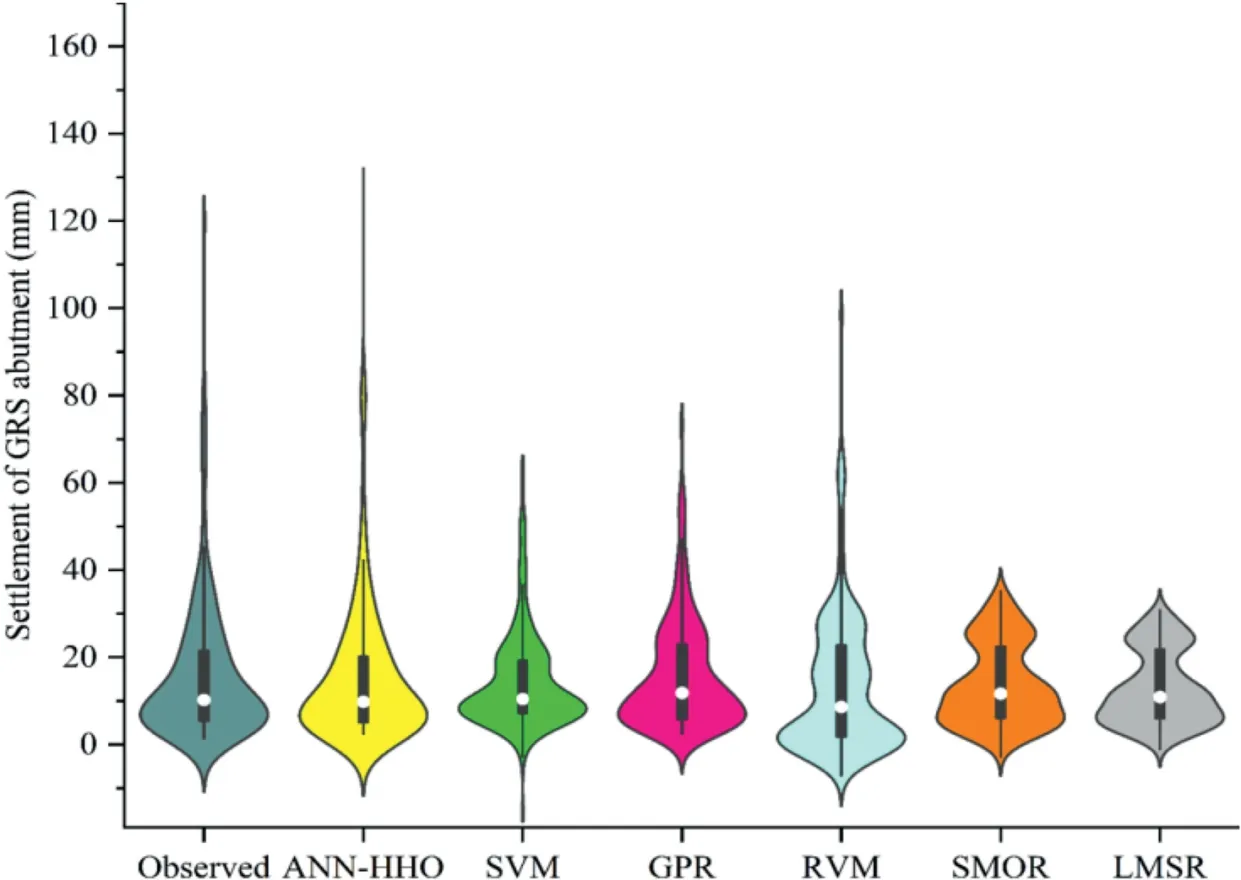
Fig.12.Visualisation of relative performance of various AI-models in replicating the distribution of observed GRS abutment settlement data via violin plots.

5.Mathematical formula for GRS abutment settlement estimation

In this section, the developed ANN-HHO model has been converted into traceable functional relationship.The mathematical formulation for ANN-based model is given as follows(Shahin et al.,2001; Khan et al., 2021):

where FHOis the transfer function between the hidden and output layers, bois the bias/threshold of output layer node, Wkois the weighted connection between kth node of a single hidden layer and output node,Wikis the weighted connection between ith input and kth node of hidden layer, Fihis the transfer function between the input and hidden layers,bhjis the bias/threshold value for node k of hidden layer (k = 1, h), Xiis the ith input node (variable), and Y represent the output variable.The weights and biases of the network are summarised in Table 10.

Table 10Weights and biases of ANN-HHO model.

For computing the settlement of GRS abutment with 8 input parameters (q, φ, J, hv, β, H, Lr/H, and B) via ANN-HHO, the relationship is given as follows:

Fig.14.Comparison of settlement values of GRS abutments predicted via ANN-HHO with the measured settlement values, and empirical methods given by: (a) Helwany et al.(2007) (dataset 1); (b) Helwany et al.(2007) (dataset 2); (c) Hatami and Doger (2021); and (d) Wu et al.(2008).

where s＇pis the normalised value of predicted GRS abutment settlement, and θkis given as follows:

It may be noted that q＇,φ＇J＇,h＇v,β＇,H＇,（Lr/H）’，and B’ denote the normalised values of the attributes.The final predicted settlement value should be de-normalised using the following equation:

where smaxand sminrepresent the maximum and minimum values of settlement for GRS abutments.A design example is presented in the Appendix section.

6.Advantages, limitations and future outlook

The proposed hybridisation of the ANN and HHO shows many advantages, such as curtailment of local minima issue, cost saving associated with experimental and FDM based modeling, and high predictive veracity.The concept of integration of mutation strategy with HHO is simple and easy to implement.Although the developed model can predict the settlement of GRS abutments in an intelligent way, yet care should be taken when applying it to the data beyond the training range of ANN.However, the model can easily be upgraded as new data are generated and made available.It is also noteworthy that the above expression is calibrated only for GRS abutments where the geosynthetic layers are laid in planar form.The wrapped form of geosynthetic layers is not considered for this work.In the future,a deep learning approach could be utilised for a more comprehensive comparison of the ML algorithms.The ensemble learning technique, which combines the output of several robust AI-based methods, might also be a useful approach in the future.

7.Conclusions

The settlement estimation of GRS abutments under service loading conditions is a difficult task for practicing geotechnical/civil engineers.In this study, a novel intelligent paradigm (ANN-HHO)has been developed and implemented for predicting the maximum settlement of GRS abutments in an intelligent way.The results of the developed ANN-HHO model have been compared with 5 MLbased robust methods, i.e.SVR, GPR, RVM, SMOR, and LMSR.The historical database generated through FDM-based analysis of validated large-scale tests in the literature was used to calibrate and validate the ML models.The following conclusions can be drawn from this research:

(1) Among all the developed models, i.e.ANN-HHO, SVR, GPR,RVM, SMOR, and LMSR, the ANN-HHO model has shown superior predictive ability in estimating the settlement of GRS abutments.

(2) For combined predictive performance(training and testing),the ANN-HHO has gained the highest ranking (total score = 72) with an OBJ value of 6.52, and has met all the conditions related to the multi-criteria approach.

(3) The results of uncertainty analysis and SA have shown that the developed ANN-HHO is robust and can generalise over the given data range.

(4) The probability distribution via violin plots and results from Taylor’s diagram show that the predictions made by the ANN-HHO are associated with less bias in comparison to its counterparts.

(5) The predicted strength of the ANN-HHO model has also been corroborated by several large-scale experimental studies reported in the literature.The results revealed that the ANNHHO predicted GRS abutment settlement values are close to the measured values.

More importantly, the model has been converted into a simple mathematical relationship and can easily be implemented by practitioners for the preliminary design of GRS abutments.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors would like to thank Higher Education Commission(HEC) for supporting this research.In addition, we extend our appreciation to the anonymous reviewers for their valuable recommendations and insights.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2022.04.012.