A post-peak dilatancy model for soft rock and its application in deep tunnel excavation
Wuqing Ci, Hehu Zhu,b, Wenho Ling,c, Xiojun Wng,*, Chenlong Su,Xingyng Wei
a Department of Geotechnical Engineering, College of Civil Engineering, Tongji University, Shanghai, 200092, China
b State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai, 200092, China
c China Railway Construction Co., Ltd., Beijing,100855, China
Keywords:Deep excavation Post-peak dilatancy (PPD) model Alejano-Alonso (A-A) dilatancy model Soft rock
ABSTRACT The dilation angle is the most commonly used parameter to study nonlinear post-peak dilatancy (PPD)behavior and simulate surrounding rock deformation; however, simplified or constant dilatancy models are often used in numerical calculations owing to their simple mathematical forms.This study developed a PPD model for rocks(rock masses)based on the Alejano-Alonso(A-A)dilatancy model.The developed model comprehensively reflects the influences of confining pressure (σ3) and plastic shear strain (γp),with the advantages of a simple mathematical form, while requiring fewer parameters and demonstrating a clear physical significance.The overall fitting accuracy of the PPD model for 11 different rocks was found to be higher than that of the A-A model,particularly for Witwatersrand quartzite and jointed granite.The applicability and reliability of the PPD model to jointed granites and different scaled Moura coals were also investigated, and the model was found to be more suitable for the soft and large-scale rocks, e.g.deep rock mass.The PPD model was also successfully applied in studying the mechanical response of a circular tunnel excavated in strain-softening rock mass,and the developed semi-analytical solution was compared and verified with existing analytical solutions.The sensitivities of the rock dilatancy to γp and σ3 showed significant spatial variabilities along the radial direction of the surrounding rock,and the dilation angle did not exhibit a monotonical increasing or decreasing law from the elastic-plastic boundary to the tunnel wall, thereby presenting the σ3-or γp-dominated differential effects of rock dilatancy.Tunnel deformation parabolically or exponentially increased with increasing in situ stress (buried depth).The developed PPD model is promising to conduct refined numerical and analytical analyses for deep tunneling, which produces extensive plastic deformation and exhibits significant nonlinear post-peak behavior.
1.Introduction
Complete stress-strain curves can be used to analyze almost all mechanical behaviors of both rocks and rock masses,including the dilatancy, strain softening, plastic flow, and other nonlinear mechanical behaviors during loading and unloading (Crouch, 1970;Farmer,1983;Hassani et al.,1984;Medhurst,1997;Ribacchi,2000).It is difficult to develop a unified constitutive model that comprehensively reflects the nonlinear behaviors of rocks, especially considering their complex post-peak mechanical behaviors,e.g.rock dilatancy and strain softening (Desai, 2015a, b; Vakili,2016).The pre-peak behaviors of rocks and rock masses have been widely investigated and can often be characterized by linear theories,but the nonlinear behavior recognition and analysis at the post-peak stage remain a challenge.
In the continuum theory, the dilation angle is often treated as one of the most significant deformation parameters to evaluate the volume strain and expansion characteristics of geotechnical materials (Detournay,1986; Alejano and Alonso, 2005; Zhao and Cai,2010a; Arzua and Alejano, 2013; Walton and Diederichs, 2015a).An accurate dilatancy model can precisely reflect the complete stress-strain processes of rocks,especially for the plastic behaviorat the post-peak stage, which is important for studying the elastoplastic and strain-softening characteristics of surrounding rock during excavation unloading(Barton and Bandis,1982;Detournay,1986; Hoek and Brown, 1997; Alonso et al., 2003; Alejano and Alonso, 2005; Meng et al., 2021).The plastic potential functions and non-associated flow rule are often established by introducing rock dilatancy to the strength criterion to improve the numerical accuracy of deformation and volume strain of rock mass engineering (Farmer, 1983; Vermeer and De Borst, 1984; Detournay,1986; Pan and Hudson, 1988; Hoek and Brown, 1997; Sterpi,1999; Zhu et al., 2017).An accurate and reliable post-peak rock dilatancy model is of great significance for the in-depth analysis of rock deformation and refined numerical calculations.
A dilatancy model and its parameters derived from laboratory experiments based on intact rocks cannot be directly applied to engineering rock masses due to the influence of scaling effects.A simplified dilatancy model is therefore often adopted in practical engineering.It is generally assumed that the dilatancy of the rock mass is constant (Vermeer and De Borst, 1984; Hoek and Brown,1997; Xu et al., 2021a), or only related to the confining pressure(σ3) (Cundall et al., 2003; Zhu et al., 2016, 2017) or plastic shear strain(γp)(Detournay,1986;Alonso et al.,2003;Park et al.,2008).However, numerous experimental results and studies have shown that the dilatancy of rocks and rock masses presents significant σ3-and γp-dependencies (Crouch, 1970; Farmer, 1983; Hassani et al.,1984; Detournay,1986; Medhurst,1997; Ribacchi, 2000; Zhao and Cai, 2010a; Walton and Diederichs, 2015a; Rahjoo and Eberhardt,2021a), and may also be related to other factors (e.g.intermediate principal stress σ2(Rahjoo and Eberhardt,2021a,b),and stress path during loading and unloading).Triaxial compression tests have indicated that the stress-strain curves under different σ3values differ significantly(Crouch,1970;Farmer,1983;Hassani et al.,1984;Medhurst,1997;Ribacchi,2000),and a brittle rock may also exhibit ductile behavior under a high σ3value.The radial stress(σr)of the tunnel boundary is zero after excavation, while σ3increases at increasing distances from the excavation boundary,and the dilation of the surrounding rocks decreases significantly.The dilatancy gradually decreases and finally disappears at a high σ3from the tunnel wall to deeper ground.Dilatancy is also found to be heavily dependent on the historical deformation process of the rocks,such as the plastic shear strain (γp= εp1-εp3) (Farmer, 1983; Hassani et al., 1984; Detournay, 1986; Medhurst, 1997; Ribacchi, 2000;Zhao and Cai, 2010a).During the excavation process, a large differential stress (σ1-σ3) at the tunnel wall makes the surrounding rocks rapidly enter the plastic state.As γpincreases with decrease in distances from the elastic-plastic boundary to the tunnel wall,the plastic volume deformation rate (dεpv)gradually decreases and approaches zero.This process reflects the influence of plastic deformation on the dilatancy characteristics of the rocks.Therefore,the effects of σ3and γpon rock dilatancy must be comprehensively considered when analyzing the stability of surrounding rocks in detail.The oversimplified dilatancy model(e.g.a constant model,a σ3-dependent model,or a γp-dependent model)often results in less accuracy of the predicted dilatancy characteristics.It ignores the constitutive dilatancy characteristics of rock under complex stress,thereby compromising the true bulking behavior of brittle rock fracturing (Rahjoo and Eberhardt,2021a, b).
The mathematical form of the existing variable dilatancy model is relatively complex.Moreover, owing to the influence of scaling effects, whether the existing rock dilatancy model is suitable for engineering rock masses remains to be determined.Although the laboratory-derived rock dilatancy model can be used to obtain reasonable agreement with field-scale observations (for relatively massive rock masses)(Zhao and Cai,2010b;Walton and Diederichs,2015b), the model parameters cannot be obtained directly from laboratory tests because of the scale differences in small-scale rocks and engineering rock masses ranging from tens to hundreds of meters(Hoek et al.,1995;Cui et al.,2020).The displacement-based back-analysis method is therefore often used in engineering to obtain the model parameters, which are then used in subsequent predictions;however,the obtained parameters are generalized and different from those of real-world conditions (Hoek, 1999;Vardakos et al., 2016).The multiparameter model and mathematically complex model may greatly reduce the reliability and applicability in rock engineering application, and the development of a simple post-peak dilatancy(PPD)model with limited parameters is necessary in practice.
This study was organized as follows.After the Introduction,the limitations of the existing constant and variable dilatancy models were presented in Section 2.A PPD model with a clear physical meaning based on the Alejano-Alonso (A-A) dilatancy model(Alejano and Alonso, 2005) was developed, and its fitting accuracies to the dilatancy data extracted from the complete stressstrain curves of 11 different rocks were discussed in Section 3.Subsequently,the reliability and scope of application(or limitation)of the PPD model were investigated for rock mass based on the dilatancy data of intact and jointed granites,and Moura coals with different sample sizes in Section 4.In Section 5, the threedimensional (3D) elastoplastic semi-analytical solution of deep excavation that follows the strain-softening constitutive law and 3D Hoek-Brown strength criterion was deduced and the ground reaction curve (GRC) was obtained to investigate differential dilatancy behaviors of surrounding rock using different dilatancy models (e.g.constant and variable dilatancy models).Section 6 discussed the necessity and significance of variable dilatancy model in deep tunneling analysis.Finally,conclusions drawn in this study were presented in Section 7.
2.Existing dilatancy models for rocks
Obtaining the complete stress-strain curve of a rock mass to study its dilatancy characteristics is challenging, and thus the constant dilatancy model is often adopted.It assumes that the dilation angle of a rock mass does not change under the action of engineering forces.This indicates that the volume expansion rate is independent of σ3and γp, as reported by Vermeer and De Borst(1984), Hoek and Brown (1997), Alejano et al.(2010), and Walton and Diederichs (2015b), among others.
However,constant dilatancy models are usually simplified,and σ3and γpare considered to have no influence on the dilatancy characteristics of rock mass.Considering the establishment of a plastic non-associated flow rule,constant dilatancy models cannot be used to achieve a refined analysis, and the calculated results differ greatly from practical conditions (Alejano et al., 2010; Zhao and Cai, 2010b).A large amount of experimental data and studies have shown that the rock (rock mass) dilatancy is a function of σ3and γp(Crouch,1970;Farmer,1983;Hassani et al.,1984;Detournay,1986; Medhurst,1997; Ribacchi, 2000; Zhao and Cai, 2010a), and also shows σ2-dependency behavior(Rahjoo and Eberhardt,2021a,b).Representative variable dilatancy models include the A-A model (Alejano and Alonso, 2005), σ3-dependent dilatancy index proposed by Yuan and Harrison(2004),Detournay(1986)'s model,Zhao and Cai (2010a)'s model, Walton and Diederichs (2015a, c)'s model, and Rahjoo and Eberhardt (2016, 2021a, b)'s dilatancy model, among others.
Existing constant and variable dilatancy models for rocks and rock masses are summarized in Table 1.

Table 1Summary of different dilatancy models.
The constant dilation angle is convenient for engineering applications but is relatively imprecise,although displacement results based on a mobilized dilatancy model may be well approximated using an appropriate best-fit constant dilation angle.For some cases, it is often difficult to find this specific constant angle for approximating the variable dilatancy model.The existing variable dilatancy models are presented in relatively complex mathematical forms,and often include multiple parameters(e.g.3D confinement(both σ2and σ3)-dependent dilatancy model (Rahjoo and Eberhardt, 2021b) requires a maximum of 12 physically meaningful parameters), which greatly limits their application.Thus,developing a simple and reliable PPD model is necessary in practical engineering applications.
3.Development of PPD model for rocks
The Poisson's ratio is often used for analyzing the rock volume expansion behavior at the pre-peak stage.However, at the postpeak stage, the mechanical properties and volume changing characteristics of rock are relatively complex.Thus, several variable models have been developed to study the post-peak behavior of rocks.The A-A model ignores the mobilization of dilatancy that occurs between yield and PD, while some other models (e.g.Zhao and Cai (2010a)'s model, Walton and Diederichs (2015a, c)'s model,and Rahjoo and Eberhardt(2016)'s model)account for this.The overly complex or precise models that consider the full dilative spectrum (i.e.pre-PD and PPD) often introduce more parameters,which greatly reduces their reliability and applicability in rock engineering (Rahjoo and Eberhardt, 2021a, b).And in many cases,the simplification of A-A model is acceptable and reliable in practice to some extent, especially for deep excavation that shows significant post-peak behavior in that the plastic zone (or plastic flow zone)is widely distributed.Thus,the A-A model was chosen as the basis of this study.
3.1.Testing data for rock dilatancy
The dilatancy data used in this study were extracted from published complete stress-strain curves,as outlined in Table 2.The crystalline(hard)rocks category generally includes Witwatersrand quartzite, Beishan granite, Amarelo País granite, Blanco Mera granite,and Vilachán granite;the sedimentary(soft)rock category generally includes strong sandstone, silty sandstone, Moura coal,weak sandstone, mudstone and Seatearth (cotgrave).
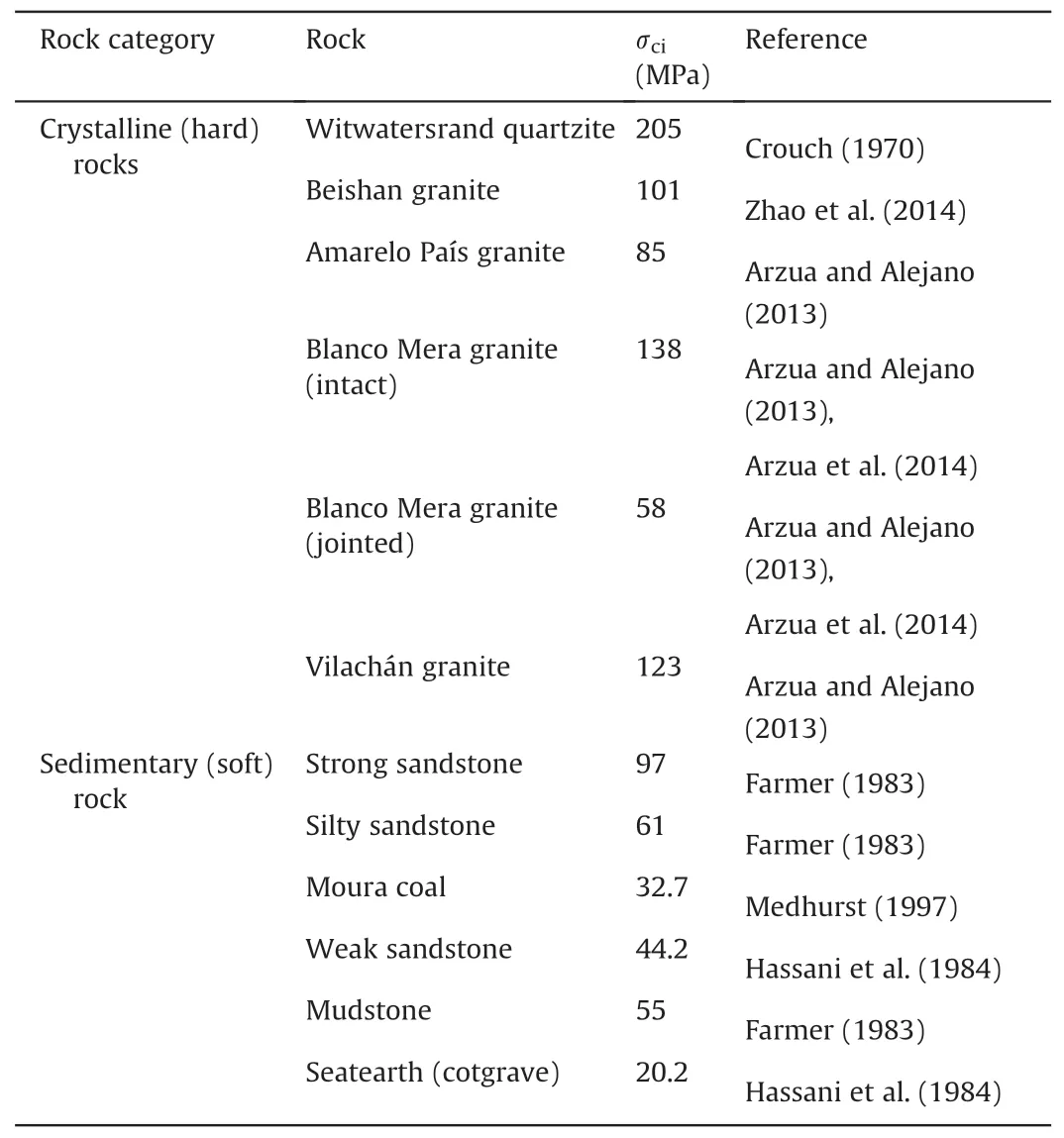
Table 2Test data for the dilation angle of rock (rock mass).
Rock (rock mass) strain can be divided into elastic and plastic strains.The plastic strain is irreversible,and the elastic and plastic strain components of rock (rock mass) can be obtained through cyclic loading and unloading tests.As illustrated in Fig.1, considering the stress-strain curve of no-cycle loading and unloading tests, the elastic modulus of the loading section is used to replace the unloading elastic modulus.
The main purpose of data processing is to obtain the irrecoverable strain locus and the curve ψ(γp).The following methods are adopted to obtain the required rock dilation angle.More specifically, the elastic strain and elastic volumetric strain can be obtained using the elastic equation:
where E is the elastic modulus, ν is the Poisson's ratio, σijis the stress component, and εeijis the elastic strain component.
The total strain of a rock can be decomposed into the elastic and plastic strains, which can be expressed as
For conventional triaxial tests,the plastic strain components are derived using Eqs.(1) and (2):
where ε1is the plastic strain,is the maximum plastic strain,εvis the volumetric strain, andis the plastic volumetric strain.
The plastic shear strain can be evaluated from Eq.(4) as
Furthermore, the dilation angle ψ = ψ(γp) can be obtained according to the-curve and is defined as follows:
The above method is used to obtain the rock dilation angle.The simplified extraction process of dilation angle can also be referred to Appendix A.More detailed methods are provided in previous literature (Medhurst,1997; Medhurst and Brown,1998; Zhao and Cai, 2010a).
3.2.A-A model
Alejano and Alonso(2005)proposed a PD model of rocks based on the peak joint dilatancy model (Barton and Bandis,1982):
where ψpeakis the peak dilation angle of rock and 0.1 is introduced to avoid numerical singularity.
The peak dilation angle is close to φ of the rock (rock mass)when σ3is small.Therefore, it can be assumed that the peak dilation angle at σ3=0 is equal to φ,and the boundary condition of this model is
The volume strain of the rock (rock mass) is the largest under low σ3or σ3=0.The plastic flow is generally assumed to follow the associated flow rule, while it follows the constant-volume nonassociated flow rule under a high σ3.Eq.(8) utilizes the peak dilation angle of the rock or rock mass under uniaxial compression as its internal friction angle, which is the basis and the boundary condition of the A-A peak dilatancy model.
Eq.(8) may be substituted into Eq.(7) to obtain the following expression (Alejano and Alonso, 2005):
Eq.(9) is the A-A peak model.For convenience, it can also be rewritten as
This model considers the influence of σ3on the peak dilation angle.Furthermore,Alejano and Alonso(2005)further proposed a negative exponential decay model to consider the influence of γpbased on the decay model reported by Detournay(1986):
where Kψ= (1+sin ψ)/(1-sin ψ), and γp,*is the maximum γp.Eqs.(9) and (11) represent the A-A dilatancy model.Alejano and Alonso (2005) concluded from their analysis of a large number of dilatancy data that γp,*has different values for different rocks.
The A-A model is composed of the σ3-dependent PD model and the γp-dependent decay model.This model has a high fitting accuracy for dilative rock testing data (Alejano and Alonso, 2005;Alejano et al., 2009, 2010; Arzua et al., 2014; Walton and Diederichs, 2015a, b).It combines the effects of σ3and γp, and utilizes the unique parameter γp,*.However, this model is composed of two equations (Eq.(9) and (11)) in its complex mathematical form.In addition, this model was established based on the dilatancy data of sedimentary (soft) rocks, and the fitting accuracy of the crystalline(hard)rock test data was not satisfactory(Zhao and Cai, 2010a; Arzua and Alejano, 2013; Walton and Diederichs, 2015a).
3.3.Existing limitations of the A-A dilatancy model
The A-A model can be written as
The dimensionless quantities ψ(σ3,γp)/φ and σ3/σciare used in this study to facilitate the comparative analysis of different models in the range of the defined domain [0,1].
The value of Δ = 0.1 in Eq.(7) is introduced to avoid the numerical singularity of the A-A model when σ3= 0.However,Δ = 0.1 is close to the magnitude of σ3= 0, and therefore the parameter α derived using the boundary condition ψpeak|σ3=0= φ will be affected by the added value 0.1, which causes a theoretical error.More generally, Eq.(9) can be rewritten as
Eq.(13) satisfies the boundary condition (Eq.(8)) and is simplified to the A-A peak model (Eq.(9)) when Δ = 0.1.The irrationality of this assumed value (Δ = 0.1) can be explained by assuming Δ = 1, 0.1, 0.01, and 0.001.Fig.2 shows the influence of σ3/σcion ψpeak/φ under different values of σciand Δ.The curves of ψpeak/φ versus σ3/σciunder different values of σciare similar because ψpeakand σ3are normalized during the calculation process.However,ψpeak/φ shows great differences under different values of Δ.The peak dilation angle under Δ=1 is 2-4 times that obtained under Δ = 0.001.Therefore, the peak dilation angle is highly sensitive to Δ, and its value should be dependent on the specific rock triaxial testing data rather than Δ=0.1 in Eq.(7).The single value Δ = 0.1 of the A-A model works well only for sedimentary rocks.
The rock dilation angle given by Eq.(12)is relatively complex in mathematical expression.The single value Δ=0.1 is not universally applicable for other rocks(besides sedimentary rock);therefore,it is necessary to properly modify the A-A model according to its limitations and propose a simple and reliable PPD model.
3.4.Development of confinement-dependent PD model
Fig.2 shows that the PD is much more sensitive to a low σ3when the value of Δ is low,and an obvious PD decay with σ3is observed at low σ3value.The added value Δ in Eq.(13) is assumed to be correlated with the rock mass quality, while σcimay be used as an important physical quantity to evaluate the rock mass quality.It can be assumed that Δ = Δ(σci) is linear, thus we have
where k varies for different types of rocks and reflects the influence of σ3on the peak dilation angle.
The peak dilation angle model can be written as
Eq.(15) is the confinement-dependent PD model.The least absolute-error fitting method and the least square method are selected to evaluate the fitting accuracies of different PD models,and the value of mean fitting deviation mf (Eq.(16)) and squared correlation (R2) are the corresponding evaluation indicators:
The data of the peak dilation angles of crystalline (hard) and sedimentary (soft) rocks are fitted using the two fitting methods,and the fitting results are listed in Table 3.It should be noted that the values of k based on the two fitting methods are very close,and the least absolute-error fitting method-based k values are selected for later analysis.
The PD model represents the nonlinear characteristics of ψpeak/φ versus σ3/σci, and the overall accuracy for the 11 rocks is satisfactory.Specifically, the PD model obtained higher fitting accuracies for sedimentary (soft) rocks than crystalline (hard) rocks in general, and the overall mf value for sedimentary (soft) rocks(0.0375)is half of that for crystalline(hard)rocks(0.0681).The silty sandstone and Seatearth (cotgrave) obtained relatively high accuracies, with mf values less than 0.02 and R2values up to 1.This is because the sensitivity of PD to σ3increases as the rock quality decreases.The PD model is therefore considered to be more suitable for lower-quality rocks, e.g.sedimentary (soft) rocks.
Meanwhile, Table 3 also suggests the reasonable (best-fitting)values of k for different categories of rocks, e.g.0.0041 for sedimentary(soft)rocks and 0.0177 for crystalline(hard)rocks.The PD model for different categories of rock could be specifically formulated as
The optimal fitting parameter of k=0.0096 was obtained for 11 different rocks.Fig.3 shows the predicted values of the PD for k=0.0001,0.1,and 0.0096.The experimental data of ψpeak/φ versus σ3/σcifor different rocks are distributed on both sides of the curve where k=0.0096.k=0.01 is used as the approximate value of the best-fit, which can be substituted into Eq.(15):
Eq.(18)is a special case of the PD model that fits well to the data of the 11 different rocks, and is referred to as the PD(k = 0.01)model.This model does not contain any unknown parameters.
The optimal value of k for a specific rock can be obtained by fitting analysis if enough data are available, but k = 0.01 is also acceptable and appropriate for the limited rock dilatancy data.It should be noted that the A-A peak model is a special case of the PD model for σci= 10 MPa.
Table 4 and Fig.4 present a comparative analysis of the prediction accuracy of the A-A peak model and PD model for different rocks.The analysis results show that: (1) The fitting accuracy of PD(k=0.01)model is lower than that of PD model because k=0.01 is a special case of the PD model,which is without exception for all the 11 rocks according to the mf value;and(2)The mf values of A-A peak model are greater than those of PD model for Witwatersrand quartzite, Beishan granite, and Amarelo Pais granite, and slightly greater than those of PD model for other 8 rocks.Therefore,the PD model provided satisfactory fitting results.

Table 3Fitting results of PD model for the PD data.

Table 4Comparison of the prediction accuracies of A-A peak model and the developed PD model.

Table 5Fitting accuracies (mf) of different dilatancy models.
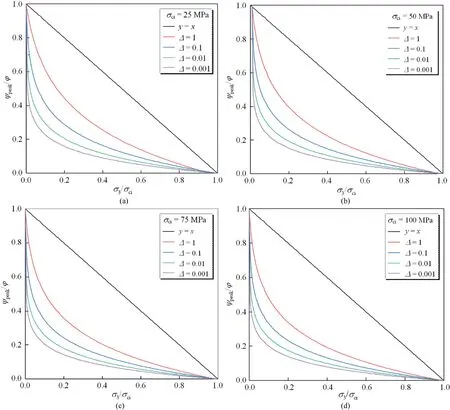
Fig.2.ψpeak/φ under different value-added Δ conditions.
The PD model is a modified model based on the A-A peak model, and provided satisfactory fitting results for the 11 rocks.It contains the single parameter k and the influence coefficient of the confining pressure, and is related to the rock physical properties.For PD(k=0.01)model,Δ=0.01 is the optimal parameter obtained based on the data from 11 rocks.No additional parameters are introduced into this model, and its accuracy is higher than that of the A-A peak model wherein the added value Δ=0.1 is arbitrary.For the PD(k = 0.01) model (Eq.(18)), both ψpeak/φ and σ3/σciare dimensionless quantities within [0,1], and there are no other variables.Different rocks can be compared within the same scale range, and the mathematical form is simplified.A-A peak model and PD(k = 0.01) model have the same mathematical expression when σci= 10 MPa,which proves the inner relationship between these two models and the rationality of PD(k = 0.01) model.
3.5.Development of confinement- and plastic shear straindependent PPD model
3.5.1.Mathematical expression of decay dilatancy model
As shown by the complete stress-strain curve (Fig.1), a rock material will undergo plastic deformation after yielding and continue to undergo loading until the peak strength is achieved.For homogeneous and isotropic rocks,the dilation angle corresponding to the uniaxial yield strength can be considered as the internal friction angle φ.Following achievement of the uniaxial yield strength, plastic deformation and strain softening occur.The dilation angle gradually decreases until the residual strength stage is reached, plastic flow occurs as the plastic strain is increased, and the dilation angle gradually approaches zero.The influence of γpon the dilation angle is similar to that of σ3.
The PPD model reflects the influences of σ3and γpon the dilation angle and should meet the following conditions:(1) It should match well with the expansion characteristics of rock (rock mass)during the development of γp, and the testing data should exhibit high fitting and prediction accuracies.(2) When γp= 0, the PPD model can be simplified into PD model, which satisfies the boundary condition ψ(σ3,γp= 0)/φ = ψpeak(σ3)/φ.(3) The mathematical form of the new model should be as simple as possible and follow the requirements of dimensional unity.(4)The parameters should be as few as possible and have clear physical and mechanical significance.
Based on extensive research and the principle of consistent dimensions, the coefficients e-γp/γp,*and 1-e-γp/γp,*are selected to investigate the decay behavior of the PD model.The following three forms of the alternative PPD models are provided.
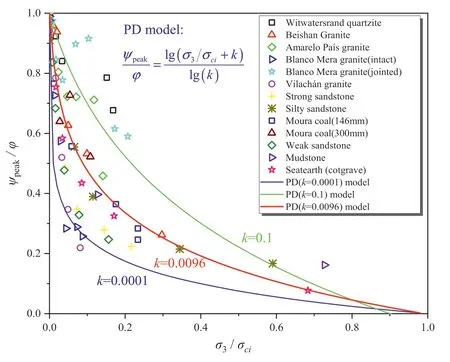
Fig.3.Samples and predicted values of the peak dilation angle for different rocks under k = 0.0001, 0.0096, and 0.1.
(1) PPD model-1
Negative exponential decay law is selected as PPD model-1,which is determined by
(2) PPD model-2
According to the previous analysis,the influence of γpon the rock dilation angle is similar to that of σ3.Therefore, considering the influence of γpat the equivalent position of the influence term for σ3, the second decay law introduces e-γp/γp,*or 1- e-γp/γp,*to the PD model, i.e.[log10σci-log10(σ3+ kσci)]/[log10σci-log10(kσci)].We found that-log10[σci(1-e-γp/γp,*)]corresponds to log10σciand log10(σ3+kσci) in terms of dimensional unity.The PPD model-2 may be written as

Fig.4.Prediction accuracies of the peak dilation angles of rock obtained using various models.
The simplified results of ψ(σ3,γp)/φ=log10[(σ3+kσci)(1-e-γp/γp,*)]/log10k also present the similar behavior as the dilatancy data show.It should be noted that singularity occurs in PPD model-2 when γp= 0.
(3) PPD model-3
Similar to the establishment of PPD model-2, the term σci(1-e-γp/γp,*) corresponds to σ3+kσciin the terms of dimensional unity.PPD model-3 is thus selected as
Similar to the A-A model, PPD model-1, PPD model-2 and PPD model-3 can be simplified into the PD model when γp= 0, and they only involve one parameter,i.e.γp,*,and each dilatancy model satisfies the boundary condition ψ(σ3,γp= 0)/φ = ψpeak(σ3)/φ when γp= 0 and 0 ≤ψ(σ3,γp)/φ ≤ψ(σ3)/φ ≤ 1.From the perspective of mathematical analysis, γp,*in the negativeexponential decay model (PPD model-1) can be the maximum of γp, which has an important physical significance.
3.5.2.Fitting accuracy of the PPD model
Since the PD model contains a single rock parameter k,while the A-A peak and PD (k = 0.01) models do not, the fitting and prediction accuracies of the PD model are significantly higher than those of the other two models.Similar to the A-A model, when studying the influence of γpon the rock dilatancy,a parameter γp,*is introduced, thereby giving the two-parameter PPD model, the single-parameter PPD(k = 0.01) model, and the single-parameter A-A model.The dilatancy data for the 11 rocks are used to evaluate the fitting accuracies of the three models,as shown in Table 5 and Fig.5.Here, the A-A model, PPD model-1 and PPD model-1(k = 0.01), PPD model-2 (k = 0.01), and PPD model-3 (k = 0.01)are evaluated and compared using the dilation angle data of 11 rocks.
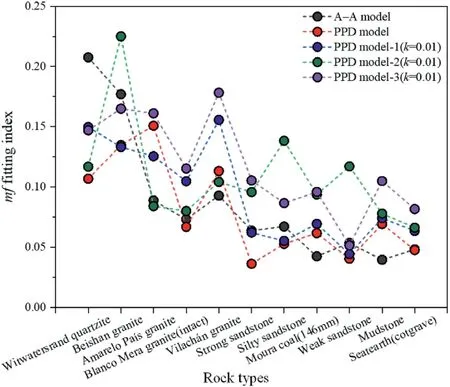
Fig.5.Fitting accuracies (mf) of different dilatancy models.
The fitting accuracy of the different dilatancy models was analyzed,and the main conclusions were as follows:(1)Similar to the fitting results of PD model in Section 3.3,a poorer-quality rock corresponds to a higher accuracy for the models.The mf values are gradually declined from Witwatersrand quartzite to Seatearth(cotgrave), which indicates that the overall fitting accuracy for the sedimentary(soft)rock is higher than that of the crystalline(hard)rocks.(2)The A-A model parameter for Witwatersrand quartzite is γp,*= - 2.31, indicating that a larger model parameter corresponds to a smaller rock dilation angle,which is the reverse of the experimental data.The mathematical form of the A-A model is not successful in fitting the dilatancy characteristics of Witwatersrand quartzite.However,for other rocks,the model parameters(γp,*)of the A-A model, PPD model (or PPD model-1), and PPD model-1(k = 0.01) demonstrate a good correlation.(3) The model parameters of PPD model-2(k=0.01)and PPD model-3(k=0.01)present large fluctuations and provide low accuracies; therefore, it is difficult to evaluate the parameters of these models when used to predict the dilatancy characteristics of rocks and engineering rock masses.(4)The fitting accuracy of the PPD model is the highest as it contains two parameters, and is more precise than the other models.The accuracy of PPD model-1 (k = 0.01) is slightly higher than that of the A-A model, while both contain the unique parameter γp,*.
Therefore,the negative exponential decay model exhibits a high overall accuracy.Similar to the A-A model,the PPD model consists of the σ3-dependent PD model and the γp- dependent negative exponential decay model.PPD model(i.e.Eq.(19))can be expressed in a simple function with a clear mechanical meaning and high fitting accuracy.
4.Verification of the PPD model and discussion on size effects
The mechanical properties of rocks and rock masses differ greatly because of the size effects.To further address these differences,testing data of intact and jointed granites(Arzua et al.,2014;Alejano et al.,2017)and Moura coal(Medhurst,1997)with different sample sizes were used to verify the PPD model and discuss its size effects.
4.1.Intact and jointed granites
Alejano et al.(2017)determined that the mechanical properties of a rock mass at the engineering scale can be tested and observed from the study of the jointed granite samples on the laboratory scale.Additionally, the rock mass parameters, e.g.GSI, can be obtained through the strength reduction of intact rock and applied to rock mass (Alejano et al., 2017).Laboratory samples with a structure similar to large-scale rock masses could provide useful information regarding rock mass behavior at the engineering scale(Archambault et al.,1993; Ribacchi, 2000; Walton and Diederichs,2015a; Alejano et al., 2017).Based on these laboratory data, the dilatancy of intact and jointed granites(rock mass)under various σ3and γpvalues was studied, and the fitting accuracy and applicability of the PPD model for granite were further evaluated.
The values of σciand φ of the intact granite are 138 MPa and 59.4°, respectively, while those of the jointed granite are 58 MPa and 39°,respectively.By analyzing the dilatancy data of intact and jointed granite samples,the fitting results provided by the different models are shown in Table 6, and the dilatancy data and fitting results of the different models are plotted in Fig.6.
It can be concluded from Table 6 that the fitting accuracy of the A-A model for intact granite is equal to that of the PPD model with mf = 0.065, but the accuracy of PPD(k = 0.01) model is low.The fitting accuracies of the PPD model and PPD(k = 0.01) model are significantly higher than that of the A-A model for jointed granite,and the developed model can be considered to have good adaptability to engineering granite rock masses.Fig.6 shows that the fitted dilation angle of jointed granite using the A-A model increases gradually as γpincreases(red curve with γp,*>0 in Fig.6),which is similar to that of Witwatersrand quartzite (Table 5).This phenomenon occurs because the complex mathematical form of the A-A model cannot consider the physical process of rock deformation and cannot truly reflect the experimental data and irreversible law of plastic deformation.Therefore,a large error will occur when the A-A model is used to evaluate the dilatancy characteristics of granite.
4.2.Moura coal tests with varying sample sizes
The complete stress-strain curves of different sample sizes are the most important data used to study the dilatancy characteristics of rock mass.Moura coal is a soft rock with a relatively large plastic shear strain.All data used in this study were collected from the same coal seam,known as the Moura DU(Medhurst,1997)to avoid the influence of different lithologies on the testing data.The experimental data are obtained by triaxial compression tests on coal samples of 61 mm,101 mm,146 mm,and 300 mm diameters,and the ratio of the diameter to the height of these samples is about 2.The digitized complete stress-strain curves for Moura coal with varying sample sizes are illustrated in Appendix B.
The physical and mechanical parameters obtained from the complete stress-strain curves are plotted in Fig.7, where σ3= 0.2 MPa is used to ensure the stability of the testing process due to the poor quality of Moura coal,and a rock strength with σ3lower than 0.2 MPa can be approximately used as σci.Fig.7 shows that σciand the mean elastic modulus(E)decrease gradually as the rock size is increased, while the elastic modulus of the same rock size with a different σ3value shows little difference.The Poisson's ratio (ν) obtained under different sample sizes also shows the insignificant effect of σ3values.The results indicate that the σciand E values of Moura coal exhibit obvious size effects,and the physical and mechanical parameters of small rocks are more sensitive to changes in sample size.The representative volume element (RVE)of the coal is approximately 300 mm.
Fig.8 illustrates the extracted results of the dilation angle and the estimation provided by PPD(k=0.01)model.The dilation angle is discretely distributed on both sides of the 3D surface of PPD(k = 0.01) model.As the coal sample size is increased, the dilation angle becomes more consistent with the 3D surface map,indicating that PPD(k=0.01)model has a higher accuracy for largescale Moura coal.Additionally,this model comprehensively reflects the variation in the Moura coal dilation angle with σ3and γpfor different sample sizes.
Table 7 and Fig.9 show the mf and γp,*distribution of the A-A model and PPD(k = 0.01) model, wherein both models have onlyone parameter (γp,*).The fitting accuracy of the A-A model for 146 mm Moura coal is slightly higher than that of PPD(k = 0.01)model, while the accuracies for the other three sizes (61 mm,101 mm,and 303 mm)are lower than that of PPD(k=0.01)model.The accuracy of PPD(k = 0.01) model for 303 mm Moura coal is mf = 0.064, which is significantly higher than that of the A-A model.The fitting accuracy of PPD(k = 0.01) model increases gradually with increasing sample size,indicating that this model is suitable for analyzing the dilatancy characteristics of large-scale Moura coals.Variation in the model parameter γp,*of the A-A model and PPD(k = 0.01) model with sample size (Fig.9) proves that an RVE of 300 mm is reasonable for Moura coal.
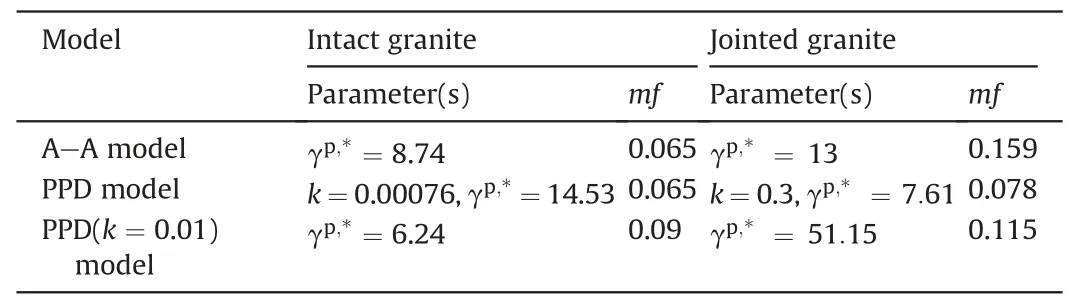
Table 6Fitting results for intact and jointed granites.
According to the rock dilatancy data of different sized Moura coals (Fig.8), the rock dilatancy gradually reduces and becomes insensitive to γpwhen γp>15%-20% for 61 mm Moura coal, after which the dilation angle is no longer sensitive to changes in γp.Therefore, a γpvalue of 20% was considered as the critical plastic shear strain, i.e.|S=61mm= 20%.Similarly, we can obtain=101mm= 30%,|S=146mm= 35%, and|S=303mm=35%.Table 5 and Fig.9 show that the γp,*value of PPD(k = 0.01)model is closer to the maximum plastic shear strain(),which is approximately twice that of the A-A model.Therefore, the parameter of PPD(k=0.01)model can be used as the approximate value of the critical plastic shear strain ().It can be speculated that the PPD model has a higher fitting accuracy than PPD(k=0.01)model because the single-parameter PPD(k = 0.01) model is a special case of the two-parameter PPD model.
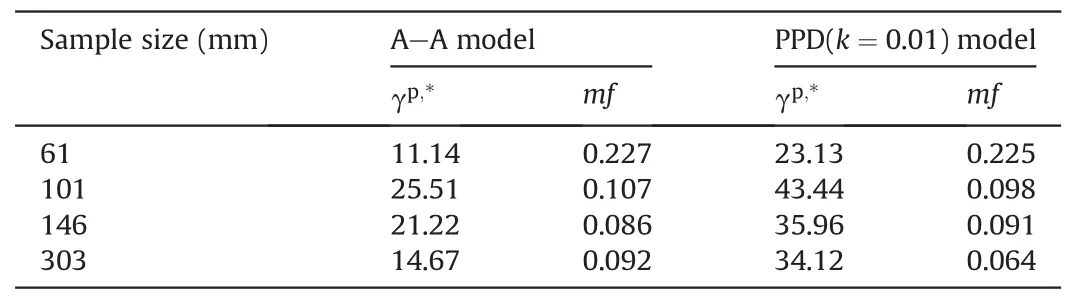
Table 7Fitting accuracy(mf) of Moura coal under different sample sizes.
Fig.10 shows the εv-ε1curves of different scaled Moura coals based on the PPD model.The digital process for obtaining εv-ε1curve is presented in Appendix C.There exist some discreteness and inconsistency in the local area, especially in the rapid change area and turning point of the εv-ε1curve.This is because: (1) The PPD model ignores the dilatancy mobilization at the pre-peak stage; and (2) The elastic stress and deformation are required in the prediction process based on the stress-strain curve(σ1-ε1),and the irregularity of stress-strain curve leads to the discreteness of the results.The PPD model-based results are highly consistent with the test results in general, especially at the post-peak stage.This also shows the robustness and stability of the PPD model for analyzing the volumetric dilatancy behavior of deep rock mass where the plastic zone is widely distributed.
5.Applications of PPD model to deep excavation in strainsoftening rock mass
The PPD model along with its non-associated flow rule was used to analyze the deep excavation of a circular tunnel.The finite difference method was used to obtain a semi-analytical solution(Lee and Pietruszczak, 2008; Park et al., 2008; Zou and Su, 2016; Guan et al., 2020; Xu et al., 2021a, b) based on the elastoplastic mechanical model of thick-walled cylinder with an infinite outer diameter.The surrounding rock is assumed to follow the strainsoftening constitutive law because it is representative fordescribing the nonlinear post-peak behavior of a typical rock mass(Han et al.,2013;Cui et al.,2017;Song et al.,2020;Zareifard,2020),and the 3D Hoek-Brown strength criterion is also considered to simulate the 3D behavior of deep rock mass.Then, the GRC of surrounding rock was obtained to analyze the differential distribution law along the radial direction using different dilatancy models and to address the advantages of the PPD model.
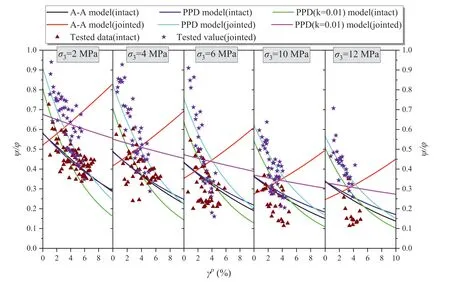
Fig.6.Dimensionless ψ(σ3, γp)/φ values obtained using different dilatancy models for intact and jointed granites.

Fig.7.Variations in σci, E, and ν with the sample size of Moura coal.
5.1.Semi-analytical solution for elastoplastic response of circular tunnel excavation
5.1.1.Rock mass models
The plastic shear strain (γp) is varied in excavated surrounding rock along the radial direction.As shown in Fig.11,the stress state of excavated rock mass consists of an elastic area,a strain-softening zone,and a plastic residual flow zone according to the distribution of strength parameters, where GSI is the most important strength parameter of the rock mass.GSI of the rock mass in the elastic area did not soften,and the corresponding parameter is GSI=GSIp.The GSI in the residual area is GSI=GSIr,and can be calculated using the following equation (Cai et al., 2007):
In the plastic zone, it is assumed that GSI follows a linear softening relationship with γp:
The 3D Hoek-Brown strength criterion (e.g.the smooth GZZ criterion) is adopted to consider the influence of axial stress (or intermediate principal stress)on the rock strength.The expression of the smooth GZZ criterion is (Cai et al., 2021, 2022):
where I1is the first stress invariant; J2is the second deviatoric stress invariant; θσis the Lode angle; and mb, s, and a are the strength parameters of rock mass.
The rock mass parameters(i.e.mb,s,and a)can be calculated as follows (Hoek and Brown,2019):

Fig.8.Tested and estimated values(PPD(k=0.01)model)of the dilation angle of Moura coal with varying σ3 and γp values:(a)61 mm,(b)101 mm,(c)146 mm,and(d)303 mm.
where miis the rock parameter,and D is the excavation disturbance coefficient.
5.1.2.Excavation response in the elastic zone
The stresses in the elastic zone are as follows:
where σθ, σr, and σzare the circumferential, radial, and axial stresses, respectively; rcris the critical radius of the rock at the elastic-plastic boundary;p is the in situ in-plane stress;q is the in situ out-of-plane stress; and pcris the critical radial stress at the elastic-plastic boundary.
The circumferential strain (εθ), radial strain (εr), and radial displacement (ur) of the rock can be calculated as
5.1.3.Excavation response in the plastic zone
The plastic zone can be divided into n rings, and the radius of each ring can be normalized as
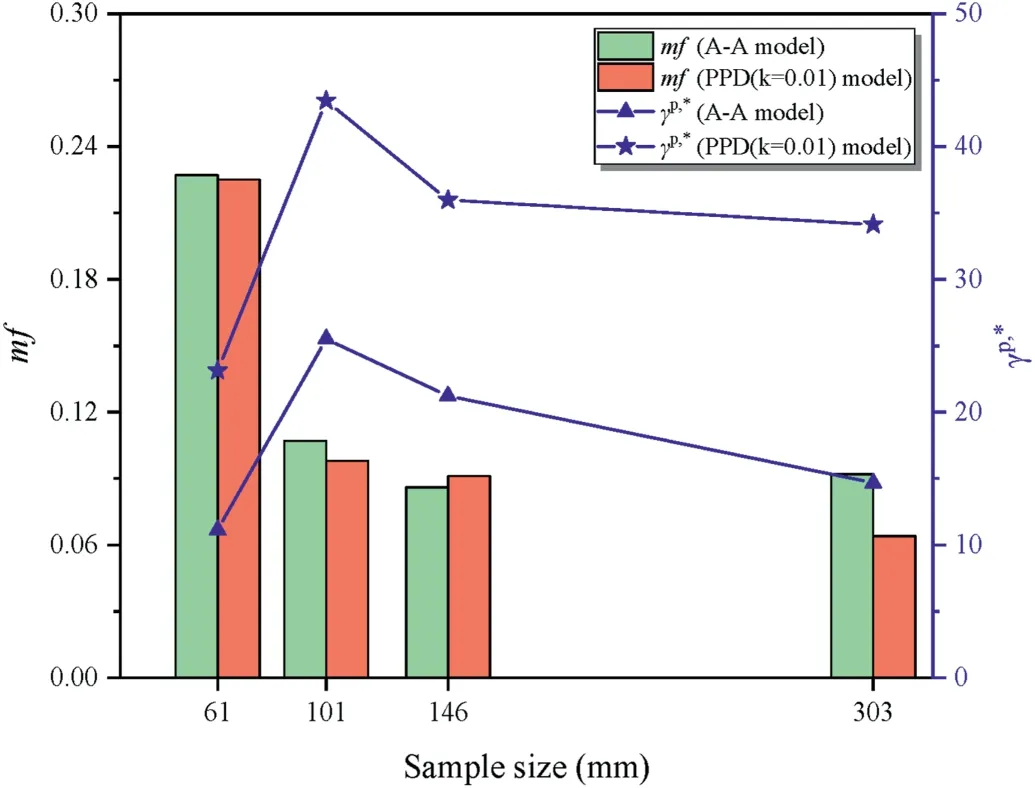
Fig.9.Fitting accuracy (mf) and γp,* distribution of Moura coal of different sample sizes.
The critical radius of the elastic-plastic boundary is treated as the first ring (i = 1), and ρ(0)= 1.ρ(n)= r0/rcris the normalized radius at the tunnel wall(i=n).The stress increment between each pair of rings is Δσr= σr(i)- σr(i-1)= - (pcr- pi)/n, where piis the support force at the tunnel wall.
At the elastic-plastic boundary, σθ, σr, and σzsatisfy the following relationship:
The stresses are governed by the elastic stress and plastic strength criterion for the rock at the elastic-plastic boundary.The stresses of the rock at elastic-plastic boundary can be iteratively computed by Eqs.(29) and (24).
In the plastic zone,σr(i)= σr(i-1)-Δσr.The corresponding σθ(i)and σz(i)could not be calculated based on the single equation of strength criterion (Eq.(24)), and thus Eq.(29), which was developed for the plane strain model in the plastic zone by Deng et al.(2008), can be used as the independent equation to obtain the plastic stresses:
where ψ(i)is the dilation angle of the ith rock ring, which can be calculated by the PPD model developed in this study:

Fig.10.εv-ε1 curves of the different scaled Moura coals based on the PPD model: (a) 61 mm, (b) 101 mm, (c) 146 mm, and (d) 303 mm.

Fig.11.Correspondence between the surrounding rock divisions and strength on the π plane.
The stresses of the rock in the plastic zone can be iteratively computed by Eqs.(31) and (24).These stresses also satisfy the equilibrium equation:
The difference form of Eq.(32) can be written as
The solution of Eq.(33) is
The strain of the ith ring in the plastic zone is decomposed into
where Δεeand Δεpare the elastic and plastic deformation increments, respectively.The elastic strain could be obtained by Hooke's law.
The strain satisfies the compatibility equation (Florence and Schwer,1978):
Eq.(36)can also be written as follows by expressing the strain as the sum of the elastic and plastic strains:
The difference form of Eq.(37) is
where λ(i)is the non-associated flow coefficient:
where ψ(i)can be calculated by the PPD model,as shown in Eq.(31).
Substituting Eq.(41) into Eq.(38), we obtain
where η(i)= 1/(1 -ρ(i-1)/ρ(i)).
The plastic strain component is therefore obtained using Eq.(42),and urcan be solved using ur(i)= -εθ(i)r(i).ρ(n)and rcr= r0/ρ(n)can also be obtained.Finally, r(i)can be obtained using r(i)=
rcrρ(i).
5.2.Verification of semi-analytical solution with existing theoretical results
The tunnel radius is set as r0= 8 m, and the rock mass parameters are GSI=50,σci=40 MPa,E=5 GPa,ν=0.35,mi=8,D=0,pi=2 MPa,φ=50°,γp,*=2.5%,and p=q=30 MPa.The stress and deformation calculation process in Section 5.1 was applied,and the constant and variable dilatancy models were used in our analysis.
The semi-analytical solution adopted in this study is verified and compared using the methods developed by Lee and Pietruszczak (2008), Xia et al.(2018), and Wang et al.(2021).Their methods apply to the case where the dilation angle is constant and the non-associated plastic flow coefficient λ is assumed to be unchanged.While the method proposed by Lee and Pietruszczak(2008) is primarily developed based on two-dimensional (2D)
Hoek-Brown strength criterion, the methods given by Xia et al.(2018) and Wang et al.(2021) are primarily developed based on the 3D Hoek-Brown strength criterion (GZZ).

Fig.12.Mechanical response of surrounding rock using constant dilatancy model(ψ=φ/2,and ψ=0)and PPD model based on the 2D Hoek-Brown strength criterion:(a)Stresses(σθ and σr); and (b) Displacements.

Fig.13.Mechanical response of surrounding rock using constant dilatancy model(ψ=φ/2,and ψ=0)and PPD model based on the GZZ strength criterion:(a)Stresses(σθ and σr);and (b) Displacements (ur).

Fig.14.Mechanical response of the surrounding rock under constant model and PPD model: (a) Mechanical responses; and (b) Dilation angle distributions.
Fig.12 shows the Hoek-Brown criterion-based comparison results of this study and the method developed by Lee and Pietruszczak (2008), and Fig.13 shows the comparison of the GZZ strength criterion-based results of this study and the methods suggested by Xia et al.(2018) and Wang et al.(2021).The applied dilatancy models consist of constant model(ψ=φ/2,and ψ=0)and the variable PPD model.
Figs.12 and 13 show that the mechanical responses for the PPD model and the semi-analytical methods used in this study have no significant difference, especially for the surrounding rock stresses(Figs.12a and 13a).However,there is a significant difference in the convergent displacement between the PPD model and the Lee and Pietruszczak (2008)'s method, and the relative errors are 19.4%,7.63%,and-9.54%for the dilatancy models with ψ=φ/2 and ψ=0 and PPD model, respectively.Additionally, the mechanical responses based on the Hoek-Brown criterion show higher divergences in peak strength, plastic zone radius, and convergent deformation compared with the GZZ strength criterion, showing significant effects of intermediate principal stress (σ2).Thus, we adopted the GZZ strength criterion for this study.The above comparisons suggest that the semi-analytical method developed in this study is reliable.
5.3.Deformations and GRCs of a circular tunnel excavation
Fig.14a shows the mechanical response of tunnel excavation under different dilatancy models, wherein the dilation angle has a limited effect on the stresses of the surrounding rock.The dilation angle is a deformation parameter,which has a great impact on the plastic internal variable (e.g.γp).γpis directly related to the softening-strength parameter, i.e.GSI(γp), of the rock mass in the plastic zone, and the surrounding rock stresses are indirectly correlated to the dilation angle according to the numerical calculation for the strength criterion.As shown in Fig.14a,the stress and displacement under the constant dilatancy model of ψ = φ/2 are separated from other dilatancy models.A larger dilatancy often corresponds to a larger radius of the plastic zone and a smaller strain-softening zone.The radius of plastic zones using the constant dilatancy models with ψ = φ/2, φ/4, φ/8, φ/16, and 0, and our developed model are 16.99 m,16.42 m,16.12 m,15.96 m,15.81 m,and 16.32 m, respectively.However, the dilation angle has a considerable influence on the deformation of the surrounding rock,and there are obvious differences in the radial displacement under different dilatancy models.At the depth of the surrounding rock,urobtained by the different dilatancy models is zero.The urvalue obtained by the variable dilatancy model is close to that obtained by the model with ψ = φ/8 at the elastic-plastic boundary but gradually approaches that obtained by the model with ψ = φ/4 near the tunnel wall.

Fig.15.GRC curves under different rock dilatancy models.
According to the rock dilatancy characteristics,larger σ3and γpvalues correspond to a smaller dilation angle.As shown in Fig.14b,the dilation angle initially increases and then decreases for the rock from the elastic-plastic boundary to the tunnel wall.Overall, the dilation angle at the elastic-plastic boundary (point A) is greater than that of the tunnel wall(point C),indicating that the effect of γpon the rock dilatancy is more obvious than σ3.However, the sensitivities of the rock dilatancy to γpand σ3show significant spatial variabilities.σ3gradually decreases and γpgradually increases from A to B, but the rock dilation angle increases gradually, which indicates that the rock dilation angle is more sensitive to changes in σ3, i.e.|dψ/dσ3|>|dψ/dγp|.Similarly, the rock dilation angle is more sensitive to changes in γpin the area of B-C, i.e.|dψ/dσ3|<|dψ/dγp|.
The maximum dilation angle is 7°(nearly φ/7)at point B,where the sensitivities of σ3and γpto the rock dilatancy reach an equilibrium state, i.e.|dψ/dσ3| = |dψ/dγp|.Although σ3is small near the tunnel wall (point C), the large γpcauses the rock dilatancy to approach zero,which indicates that γpcontributes more to the rock dilatancy in the plastic zone.The dilation angle initially increases and then decreases from A to C, presenting σ3- or γp-dominated differential characteristics of rock dilatancy.This phenomenon(change law)along the tunnel radius direction based on PPD model cannot be exactly displayed by any other constant dilatancy model.
The GRC and the support characteristic curve (SCC) are often used for surrounding rock stability analysis and design.As shown in Fig.15, the GRC curves obtained based on different dilatancy models have obvious differences.Large differences also exist in the support stiffness under different dilatancy models.For example,in Fig.15,we assume that the displacement release amount is 0.02u*,the convergence displacement of the surrounding rock is 0.04u*,the required support stiffnesses based on the constant dilatancy model (ψ = φ/k(k = 2, 4, 8, 10), and ψ = 0) and the variable dilatancy models (PPD model and A-A model) are 5.15, 2.33,1.33,0.92,0.58,1.58,and 0.76,respectively.In this case,the PPD modelbased support stiffness is between those obtained by the models with ψ = φ/4 and ψ = φ/8,and it was close to the result obtained by the model with ψ = φ/8 when the support reaction force(pi)is small.However,the A-A model provides a result close to the result obtained by the model with ψ = φ/16, presenting the similar behaviors as very poor-quality soft rock.
According to the constant dilatancy value recommended by Hoek and Brown(1997),ψ = φ/8 is acceptable for average-quality rock mass (e.g.GSI = 50).This recommendation is consistent with the PPD model-based prediction results for unsupported surrounding rock (pi= 0) in this calculation, but it does not produce reliable results for supported surrounding rock (pi≠0), thereby reflecting the limitation of the constant dilatancy model and its inapplicability to complex engineering problems.
The shape of the convergence profile for the variable dilatancy model has no significant difference compared to those obtained using constant dilation angles, which is consistent with the conclusions made by Walton and Diederichs(2015b).The relative error of convergence displacements between the PPD model and the constant dilation angle suggested by Walton and Diederichs(2015b) (i.e.ψ = 0.1409φ) is less than 10%, and this difference is acceptable within the allowable engineering error range.However,in engineering numerical simulations and tunnel design,it is often difficult to find the specific constant dilation angle for approximating the variable dilation angle.There also exist considerable differences in the dilation behavior predictions of surrounding rock between the constant and variable dilatancy models, as shown in Fig.14b.The use of variable dilatancy model is conducive to enhance the understanding of the nonlinear characteristics of surrounding rock dilatancy.
6.Discussion
6.1.Application of the developed dilatancy model
The fitting results of rock dilatancy data of 11 different rocks in Sections 3.3 and 3.5 show that the PPD model has good applicability to soft rock (or sedimentary rock), and the prediction accuracy of the PPD model for jointed granite is higher than that for intact granite in Section 4.1.PPD model also obtains better accuracies for large-scale Moura coal compared with the small-scale ones in Section 4.2.These results may demonstrate that the PPD model has good applicability for large-scaled soft rock (e.g.engineering rock mass)and can also be used for deep rock engineering with soft rock properties under high stress states.This may be supported by the viewpoint that the laboratory results can be used to analyze behaviors in practical engineering if the structural plane of the rock mass is reasonably considered (Detournay, 1986;Alejano and Alonso, 2005; Zhao and Cai, 2010a, b; Arzua et al.,2014; Walton et al., 2015; Alejano et al., 2017), e.g.the comparisons of intact and jointed granites and small- and large-scaled Moura coals in our study.
6.2.Consistency and particularity of pre-peak Poisson effect and PPD behavior
The dilation angle under conventional triaxial state can be expressed as (Vermeer and De Borst,1984):
It can be deduced from Eq.(43) that
Poisson's ratio in the elastic stage is expressed as ν = - dεe3/dεe1.Similarly, the Poisson effect in the plastic stage may also be characteristic by Eq.(44).
Eq.(44) presents the approximate relationship between the dilation angle and Poisson's ratio in the plastic zone.ν = 0.5 is obtained when ψ = 0,which is in accordance with the assumption made in the analytical analysis for studying the pre-peak elastic behavior of surrounding rock.Eq.(44) therefore shows the similarity of pre-and post-peak behaviors.The constant Poisson's ratio is often used in the pre-peak stage to analyze the elastic Poisson effect and deformation characteristics.However, the complex PPD behavior of surrounding rock in the plastic zone determines the complexity of the Poisson effect, especially for deep soft rock tunnels where the plastic zone is widely distributed.The Poisson effect in the plastic zone therefore presents a particularity unlike that in the elastic zone,and it is obvious that the constant dilatancy model cannot accurately reflect the complex Poisson effect of surrounding rock at the post-peak stage.This perspective is consistent with Rahjoo and Eberhardt (2021a).
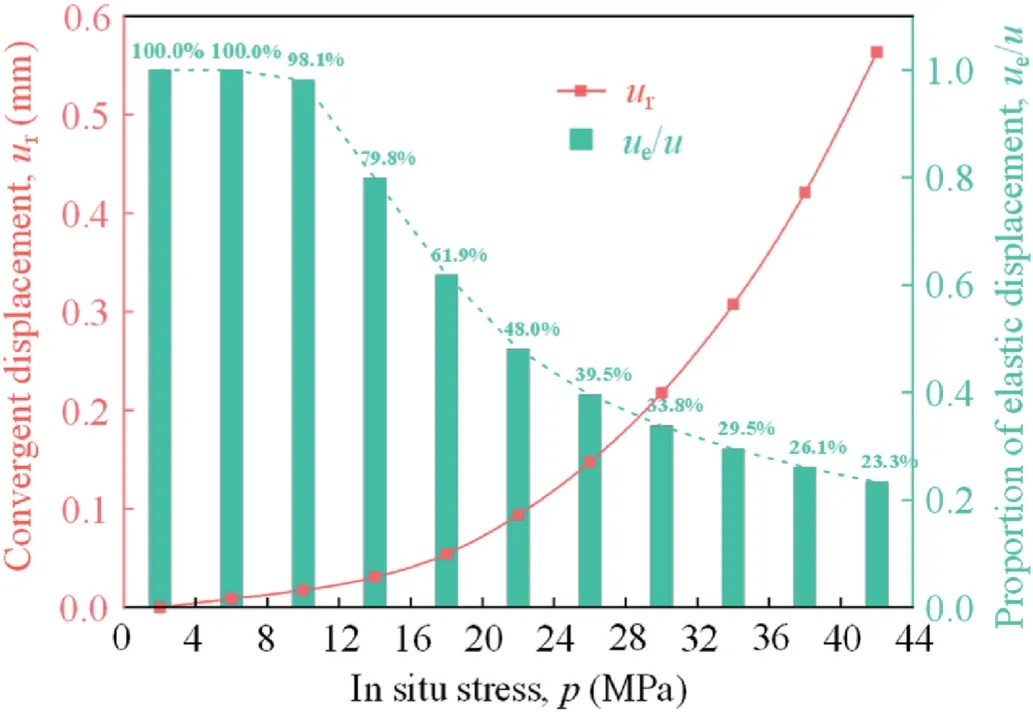
Fig.16.Convergent displacements under different in situ stresses (p).
6.3.Convergent displacements of surrounding rocks under different stress levels
Fig.16 shows the convergent displacements of surrounding rock under different stress levels (buried depths).The deformation shows a nonlinear increasing trend with the increasing stress,which can be described by a parabola or exponential approximation.Meanwhile, the tunnel at a low in situ stress (i.e.lower than 8 MPa) is completely dominated by elastic stress; however, the elastic proportion decreases rapidly in the medium in situ stress region(i.e.from 10 MPa to 30 MPa),and finally slowly tends to zero at a high in situ stress, which indicates that the deep tunneling is governed by plastic deformation under a high stress state.
Excavation in a shallow tunnel mainly produces elastic deformation,and the pre-peak behavior of a rock mass based on elastic theories is relatively simple in numerical calculations and analyses.However, deep excavation induces a wide range of plastic zones,especially for a strain-softening rock mass that shows obvious PPD behavior under a high ground stress.The simple dilatancy model cannot accurately reflect the post-peak behavior and results in a significant error in the calculation.Therefore, a reasonable PPD model (e.g.our developed PPD model) is necessary for deep tunneling analyses.
7.Conclusions
This study discussed the application limitations of the constant dilatancy model and the influences of σ3and γpon rock PPD behaviors.A PPD model was developed based on the widely used A-A model.The PPD model has a simple mathematical form and comprehensively considers the influences of σ3and γpon rock dilatancy.
The accuracy and applicability of the PPD model and the A-A model were compared and analyzed based on the rock dilatancy data of 11 different rocks, intact and jointed granite, and Moura coals of different sample sizes.The overall fitting accuracy of the PPD model for these rocks was found to be higher than that of the A-A model, and the fitting accuracies of the PPD model for sedimentary (soft) rocks and large-scale rocks were higher than those for crystalline (hard) rocks and small-scale rocks.Therefore, the developed dilatancy model is more suitable for describing the PPD behavior of engineering soft rocks.
The influence of rock dilatancy on the mechanical response of a circular tunnel excavated in strain-softening rock mass was also studied.It was found that the sensitivities of the surrounding rock dilatancy to γpand σ3present significant spatial variabilities along the radial direction of the tunnel.The dilation angle did not present monotonically increasing or decreasing trend from the elasticplastic boundary of the surrounding rock to the tunnel wall,showing the σ3- or γp-dominated differential characteristics.The refined analysis of complex tunnel excavation must incorporate the variable dilatancy model to accurately reflect the post-peak behavior of surrounding rocks, particularly for deep tunneling,which is governed by high stresses and a widely distributed plastic zone.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was funded by a Special Fund for Basic Research on Scientific Instruments of the National Natural Science Foundation of China (Grant No.41827807) and the Study on Intelligent Technology for Tunnels Construction of Sichuan-Tibet Railway (Grant No.19-21-1).
Appendices A-C.Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2022.05.014.
 Journal of Rock Mechanics and Geotechnical Engineering2023年3期
Journal of Rock Mechanics and Geotechnical Engineering2023年3期
- Journal of Rock Mechanics and Geotechnical Engineering的其它文章
- Development of mathematically motivated hybrid soft computing models for improved predictions of ultimate bearing capacity of shallow foundations
- Effects of intermediate stress on deep rock strainbursts under true triaxial stresses
- Numerical simulation of fatigue crack propagation in heterogeneous geomaterials under varied loads using displacement discontinuity method
- Combined load bearing capacity of rigid piles embedded in a crossanisotropic clay deposit using 3D finite element lower bound
- Long-term decay of the water pressure in the osmotic tensiometer
- Predicting and validating the load-settlement behavior of large-scale geosynthetic-reinforced soil abutments using hybrid intelligent modeling
