Analysis of stresses at the center of transversely isotropic Brazilian disk

Ali Aminzadeh, Florian Amann

a Institute of Geology of the Czech Academy of Sciences, Prague, Czech Republic

b Chair of Engineering Geology, RWTH Aachen University, Aachen, Germany

Keywords:Brazilian test Transverse isotropy Rock anisotropy Anisotropic disk Tensile stress Shear stress

ABSTRACT This article presents the stresses at the center of a Brazilian disk(BD)for transversely isotropic rocks.It is shown that the solution of stresses at the center of an anisotropic disk is a function of the disk radius and the magnitude of applied load, as well as the material orientation with respect to the load axis and two dimensionless ratios with specific physical meanings and limitations.These two dimensionless parameters are the ratios of Young’s modulus and apparent shear modulus,although the ratio of apparent shear modulus will be eliminated if the Saint-Venant assumption is considered.Considerable finite element simulations are carried out to find the stresses at the disk center concerning the material orientation and the two dimensionless parameters.Also, an approximate formula obtained from analytical results,previously proposed in the literature for solving the tensile and compressive stresses at the disk center,is re-written and simplified based on these new definitions.The results of the approximate formula fitted to the analytical results are compared to those obtained from numerical solutions, suggesting a good agreement between the numerical and analytical methods.An approximate equation for the shear stress at the disk center is also formulated based on the numerical results.Finally, the influence of the assumptions for simplification of the proposed formula for the tensile, compressive, and shear stresses at the disk center is discussed, and simple and practical equations are proposed as estimations for the stresses at the center of the BD specimen for low to moderate anisotropic rocks.For highly anisotropic rocks, the reference plots can be used for more accuracy.

1.Introduction

Brazilian disk (BD) specimen, first proposed for concrete by Carneiro (1943) and Akazawa (1943), has been widely used for determining the tensile strength of rock materials due to its corebased configuration which needs minimal machining, its ability to evaluate the anisotropy effect of the material by rotating the specimen, application of compressive load instead of tensile load,and the simple loading configuration which exists for any compression loading machine.This method is suitable for brittle materials which have smaller tensile strength compared to the compressive strength.In these materials,it is preferable to find the tensile strength due to the compressive loading.Another key application of this test is to find the elastic constants of the materials(Wang et al.,2004;Chou and Chen,2008;Japaridze,2015).For both goals,one needs to first determine the stress field on the disk surface.Note that the stresses needed for the determination of elastic constants are expected to remain in the elastic range of the material behavior, whereas the critical stresses required for the measurement of strengths may exceed this range because of the nucleation of micro-cracks in the specimen before its failure.Besides, various types of BDs such as the through-thickness cracked BD(Fowell,1995;Aminzadeh et al.,2019)and double-edge notched BD (Chen et al., 2003; Aminzadeh et al., 2022) are used for the determination of mode I and mode II fracture toughnesses of rock materials,respectively.The BD test,instead of the direct tension,is also widely used to measure the tensile strength of coal because of its low tensile strength(Zhang et al.,2021),although it is difficult to analyze the results due to the complicated internal structure of coal(Li et al., 2016).

Fig.1 schematically illustrates a transversely isotropic disk with an orientation of the plane of isotropy β with respect to the load axis.To conduct the BD test,the specimen is loaded by two vertical compressive line loads (P) through the thickness of the specimen(B).When β = 0°and 90°, the shear stresses across the isotropyplane are zero at the disk center but for other cases, the shear stresses must also be considered.

In a great number of studies (Istvan et al.,1997; Khanlari et al.,2015; Jamshidi et al., 2021), the tensile strength (σt) of anisotropic rocks at the center of BD specimen has been simply obtained through the isotropic formula suggested by the American Society for Testing and Materials(ASTM D3967-08,2008)and International Society for Rock Mechanics(ISRM,1978)as σt=P/(πRB),where P is the failure load,and R and B are the radius and thickness of the disk,respectively.However, due to the presence of weak planes, the anisotropic solution should be applied to accurately assess the stresses in an anisotropic disk under compressive loading even if the isotropy plane is normal or parallel to the loading direction.Okubo (1952) and Lekhnitskii (1968) were two of the pioneers in considering the anisotropic analytical solution of the stress field in BD specimens.Based on their method, Amadei et al.(1983), Chen(1996) and Claesson and Bohloli (2002) presented several charts for determining the dimensionless stresses at the disk center as a function of four elastic constants, i.e.E, E＇, ν＇, and G＇(ν = ν＇E/E＇).Some of the researchers tried to reduce the elastic constants to fewer dimensionless parameters and re-wrote the analytical solutions based on these parameters.Chen (1996) used three dimensionless parameters:ξ=E/E＇,η=E/G＇,and ν＇,whereas Claesson and Bohloli(2002)used a pair of dimensionless factors ξ=E/E＇and η =The parameter η in both methods is merely a mathematical definition without a specific physical meaning and limitation.Besides, Claesson and Bohloli (2002) proposed an approximate equation for calculating the tensile and compressive stresses at the disk center.However, the shear stress, which is of great importance in determining the elastic parameters of the material when the isotropy plane does not align parallel or normal to the loading orientation, is still lacking in the literature.Aliabadian et al.(2019)coupled analytical stress field solution with a modified Hoek-Brown failure criterion(Saroglou and Tsiambaos,2008)to present a formula for finding the strength in an anisotropic disk which is of great importance for obtaining more accurate values of the rock strength.However,this formula is dependent on various parameters, some of which must be measured from other test configurations.

A growing body of literature has been published on numerical calculation of the stress field in anisotropic BD based on finite element (FE), finite difference, boundary element, and discrete element methods (Wang et al., 2004; Chou and Chen, 2008;Mahabadi et al., 2009; Dan, 2011), most of which have tried to validate their results through experimental observations.To the best of our knowledge, a simple equation based on numerical results for practical use in stress calculation in an anisotropic disk has been lacking.

It is useful to note that the expected splitting in a disk specimen due to the tensile failure does not necessarily occur in experimental tests.Therefore, one should be cautious about considering the maximum tensile stress at the center of the BD as the tensile strength.In other words,the tensile stress can be considered as the tensile strength only when the fracturing initiates at the center of the disk.Many studies have addressed this issue from numerical(Li and Wong, 2013; Ma et al., 2018), analytical (Li et al., 2016;Aliabadian et al.,2019),and experimental(Vervoort et al.,2014;Tan et al., 2015; Mighani et al., 2016) points of view.Besides, several studies have tried to propose specific loading configurations to avoid strength bias from the disk center.These configurations can be categorized into two general groups: (1) curved jaws with different radii compared to the radius of the disk, and (2) flat platens which may also include a soft cushion or a tiny hard cylinder between the loading and the tested materials(Markides and Kourkoulis, 2016).However, a flat platen may be considered as a curved jaw with an infinite radius compared to that of the disk.Apart from the mentioned tests,a specific test scheme(a flattened BD specimen) has also been proposed by Wang et al.(2004).Markides and Kourkoulis (2016) evaluated the effect of the curvature of the jaw and its stiffness on the analytical results based on two ratios:(1)the ratio of the disk radius to the jaw radius(ρ),and(2) the ratio of the Young’s modulus of the disk to that of the jaw(α).The analyses include a wide range of BD test configurations except for the flat platens with soft cushion and the flattened BD specimen.They also compared their results to that obtained for the diametral loading,i.e.when the loading is theoretically considered a point load in two-dimensional (2D) space (or a line in three dimensions(3D)).They assumed 0 ≤ρ ≤1 and 0.01 ≤α ≤0.38.ρ=1 means that the radii of the disk and jaw are equal(e.g.Erarslan and Williams,2012;Komurlu and Kesimal,2015),whereas ρ=0 shows that the radius of the jaw is infinite which corresponds to the standard method proposed by ASTM D3967-08(2008).ρ=0.67 has also been specifically taken into account due to its coincidence with the ISRM method(ISRM,1978).The upper and lower boundaries of α were obtained based on the Young’s moduli of a soft shellstone(1.5 GPa) and a hard marble (80 GPa) to the Young’s modulus of steel(210 GP),which represent a wide range of brittle materials.On one hand,their analyses have shown that the stresses at the center of the disk do not change if 0 ≤ρ ≤0.67(between ASTM and ISRM methods), but for higher values of ρ, the tensile stress at the disk center dramatically decreases leading to an overestimation in the tensile strength (Japaridze, 2015; Markides and Kourkoulis, 2016).On the other hand,for the materials that have an elastic modulus of at least 10% of the jaw proposed by ASTM or ISRM, the stresses at the disk center are almost equal.Even for α ＜0.1, the difference between the two standard methods will not exceed 2%.However,the error is not negligible for ρ> 0.67 even if α > 0.1.Therefore, it can be concluded that the stress field at the center of the BD is not sensitive to the boundary conditions as long as 0 ≤ρ ≤0.67.However, this does not ensure the validity of the tensile strength obtained from the experimental Brazilian test since due to the stress concentration,the crack initiation may deviate from the disk center.The mentioned conclusion can be extensively used to perform experiments on BDs since one can use the jaw suggested in the ISRM method (as the upper limit for ρ) to facilitate crack initiation at the disk center while the stress field at the disk center is still identical to that obtained from the ASTM method or the theoretical BD test under diametral load.

Nevertheless, our focus is on presenting the stresses at the center of the disk while it still has an elastic behavior(i.e.the stress level is about 30%-60% of its failure load) to be later used for determining the elastic constants of anisotropic materials,thus the loading frame is not crucial.For using these results for the tensilestrength, we recommend using 0 ≤ρ ≤0.67 in experiments.However,for determining the type of failure,one has to perform a set of Brazilian experiments with different angles between the loading and the material orientation and determine the type of failure for each angle by various monitoring methods like digital image correlation or acoustic emission.In this study, two dimensionless parameters with physical meanings and quantitative boundaries for characterizing the deformation of anisotropic rock materials are introduced that can even be reduced to one parameter in some special cases.The normalized stresses at the center of the disk are shown to be a function of these two parameters as well as the orientation of the material.Based on the FE simulations performed concerning these parameters, the tensile, compressive,and shear stresses at the center of the BD for a variety of anisotropy parameters are plotted and approximate equations are fitted to them.Finally, the effect of different assumptions for the simplification of this formula is evaluated and discussed.

2.Methodology

Mellor and Hawkes (1971) stated that the thickness of the disk should be more than 10 times the size of the grains to ensure that the specimen is a representative volume of the material.Besides,Yu et al.(2006)showed that a ratio of the thickness to the diameter of B/(2R)=0.2 ensures a plane-stress behavior of the disk using both 3D numerical FE simulations and experimental tests.But for higher values of B/(2R),the strength obtained from the numerical solution was less than the real strength of the rock.Li et al.(2020) studied the concurrent effect of anisotropy orientation and the disk size on the tensile strength and elastic constants of a transversely isotropic rock.They prescribed the ratio B/(2R) = 0.5 (more than the ratio proposed in Yu et al.(2006)) and considered 2R as the representative size factor.The tensile strength decreased with the disk size for 0°＜β ＜45°in their experiments.But for 60°＜β ＜90°, the tensile strength was descending with the size if 40 mm ＜2R ＜100 mm and it was ascending with the size if 20 mm ＜2R ＜40 mm.Moreover, E increased, whereas E＇and G＇decreased with the disk size.In this study, we consider the plane-stress condition, i.e.B is large enough to ensure uniformity of the specimen while B/(2R) is small enough to eliminate the effect of size on the results.

Consider the x＇y＇plane in which x＇is along the isotropic plane(x＇z＇)whereas y＇is the axis of symmetry as illustrated in Fig.2.For plane-stress(σz＇=τx＇z＇=τy＇z＇=0)deformation in the x＇y＇plane,four elastic constants are required: two Young’s moduli in x＇and y＇orientations(E and E＇),and the shear modulus and Poisson’s ratio in the x＇y＇plane (G＇and ν＇).

The 2D Hook’s law in the symmetry plane x＇y＇for the planestress condition reads

where σx＇ and σy＇ are the stresses along the directions x＇and y＇,respectively;εx＇and εy＇are the strains along the directions x＇and y＇,respectively; and τx＇y＇ and γx＇y＇ are the shear stress and strains,respectively.

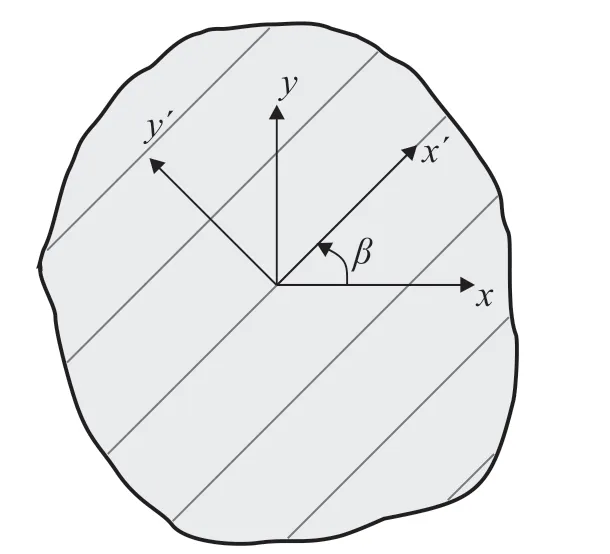
Fig.2.The principal material coordinate system x＇y＇ obtained by rotating its global coordinate system xy with an angle β.Note that the transversely isotropic material has an axisymmetric behavior considering y＇.

Eq.(1) presents the stress-strain relationship in the principal coordinate system of the material for the plane-stress conditions.If the x＇y＇coordinate system is rotated along the z＇by-β,i.e.to xy as shown in Fig.2, non-zero elements may appear in previously zero elements of the compliance matrix.According to the transformation rule (Ting, 1996), the generalized Hoek’s law for the plane-stress condition reads

or in a short form:

Here,the compliance matrix has been normalized based on two dimensionless parameters, ξ = E/E＇and η = G＇/G＇sv(Aminzadeh et al., 2019).Recently, these definitions have been used in the fracture growth criteria to predict the fracturing behavior of two different anisotropic rocks (Grimsel granite and Opalinus clay)under pure tensile loading and a wide range of mixed-mode loading conditions, and the results are compared with the experimental data (Nejati et al., 2020b,a; Sakha et al., 2022).G＇svis obtained from the Saint-Venant relation (Saint-Venant,1863) in the symmetry plane, i.e.1/G＇sv= 1/E+ （1+ 2ν＇）/E＇.It is useful to be reminded that the Saint-Venant relation is converted to the wellestablished relation 1/G = 2(1 + ν)/E in the isotropic plane.η and ξ are the ratios of the shear and Young’s moduli with specific physical meanings and boundaries in transversely isotropic rocks.Surveys such that conducted by Amadei(1996)have shown that 1＜ξ ＜4 for most anisotropic rocks.Although, Worotnicki (1993)showed that ξ can even be close to 6 for rocks such as pelitic clay and pelitic micas.Also, extensive experimental research on 200 specimens has shown that G＇svis a proper estimation for G＇in a wide range of anisotropic rocks, especially for the rocks with ξ ≤2(Worotnicki,1993).Thus,η is expected to be close to unity which is in good agreement with the literature survey reported by Aminzadeh et al.(2019).Based on the mentioned survey, 0.8 ＜η ＜1.2 for more than 70% of the reported results from 12 independent studies,although a few data are reported to be out of 0.7 ＜η ＜1.3.Besides, 0 ＜ν＇＜0.5 based on Aminzadeh et al.(2019) for the common rock materials,most of which are concentrated in the range of 0.1 ＜ν＇＜0.3.Moreover, the elastic constants are limited due to thermodynamic restrictions as E, E＇, G, G＇> 0, -1 ＜ν ＜1,and - [1 -ν/(2ξ)]0.5＜ν＇＜[1 -ν/(2ξ)]0.5(Amadei et al.,1992).

The deformation problem shown in Fig.2 is solved by the Airy stress function (φ) which leads to a quartic equation called the characteristic equation (Lekhnitskii,1968):

One can find the complex parameters in two ways: (1) by substituting the elements of the generalized compliance matrix from the rotated plane xy in Eq.(5),or(2)by replacing the elements of the compliance matrix from the principal coordinate system x＇y＇in Eq.(5)and then transforming the results to the xy plane,as will be explained in the following paragraphs.

Here, the second method is used to avoid lengthy relations although the outcome will be the same.Substituting the elements of the matrices from Eq.(1) into Eq.(5) and arranging the results based on ξ and η, the plane-stress characteristic equation for the principal coordinate system is calculated:

where~μ is the complex parameterin theprincipal coordinatesystem x＇y＇.For the plane-stress solution,we have proved that the effect of the term 2ξν＇(1 - η)/η on the complex parameters ~μ1and~μ2is insignificant considering the error bound of rock materials(Aminzadeh et al.,2019).Therefore,Eq.(6)will be simplified to

The complex parameters for the plane-stress condition, obtained from Eq.(7), only depend on the ratios of Young’s modulus(ξ) and shear modulus (η):

In general, the complex parameters ~μ1and ~μ2in the x＇y＇plane are calculated from Eq.(6),and then the transformed parameters μ1and μ2in the xy plane are obtained from Lekhnitskii (1968):

As can be readily seen from Eq.(9), the deformation of a transversely isotropic plane is characterized by the orientation of material (β) and the complex parameters in the principal coordinate system（~μk）.Note that the complex parameters are dependent on the elastic constants as well.Now, the Airy stress function is used to obtain the planar stresses:

Note that φ(x,y)=2Re[F1(z1)+F2(z2)]is the Airy stress function,and Φ1(z1) = dF1/dz1and Φ2(zz) = dF2/dz2are the new complex potentials from which the stresses are calculated as

3.Results

3.1.FE simulations

Using the FE method,the stresses at the center of the disk were calculated for different anisotropy parameters(ξ,η,and β).ABAQUS(ABAQUS/CAE, 2014) was used for modeling a 2D anisotropic BD specimen.The simulation was performed using plane-stress quadrilateral elements.To include the elasticity anisotropy, the anisotropy elasticity module was employed and all the elastic constants were defined in a way to correspond with the dimensionless parameters ξ = 1,1.5, 2, 3, 4, and 5 and η = 0.7,1, and 1.3.The value of G＇svwas obtained by assuming ν＇=0.1 which had to be converted to ν as an input of the software shown as ν12in ABAQUS.It should be remembered that ν and ν＇are related through the symmetry of the elasticity matrix, i.e.ν =ξν＇.The global Cartesian coordinate system was considered in the xy direction and the material was oriented at β=0°,15°,30°,45°,60°,75°,and 90°around the center of the disk (refer to Fig.1).In ABAQUS, the elastic constants in the local coordinate systems (aligned with the principal material orientations)are used as inputs to formulate the elasticity matrix.Then, the transformation laws are used to transform this matrix into the global coordinate system to be employed for the calculation of the stiffness matrix in the global coordinate system.A typical FE mesh along with the loading condition used for the BD specimens is shown in Fig.3.Two compressive line loads(P/B)were applied in opposite directions through the entire thickness of the specimen.A total of 315 FE simulations were conducted in ABAQUS to obtain the stresses at the center of the BD specimen considering different combinations of materials properties (ξ and η) and orientations (β).Additional simulations were performed to evaluate the effect of changes in the value of ν＇on the stresses at the disk center.

By assuming an elastic behavior,the shear stresses at the center of the isotropic materials are expected to be zero.However, foranisotropic materials,this is only true if the isotropic plane is along or normal to the load direction, i.e.β = 0°and 90°.The reason behind this is the direct effect of β on μ1and μ2(Eq.(9)), which in turn affects the solution of the shear stress through Eq.(11).Therefore, the shear stresses at the disk center for 0°＜β ＜90°must also be taken into account.

Fig.3.The mesh and the loads used during the FE modeling of the BD specimen.

3.2.Plots for the normalized stresses at the center of the BD

According to the outcomes obtained in Section 2, the in-plane stresses (tensile, compressive, and shear stresses) at the center of the BD specimen for a transversely isotropic rock depend on three anisotropy parameters:ξ,η and β.Besides,the effect of geometry R and loading P must be taken into account.Thus, the stress at the center of a disk is a function of geometrical, loading, and material parameters,i.e.σ=F(R,P,ξ,η,β).Now,let us assume an anisotropic disk with radius R and thickness B which is loaded by force P, as depicted in Fig.1.The stresses at the center of the disk are normalized to ~σx, ~σy, and~τxyas

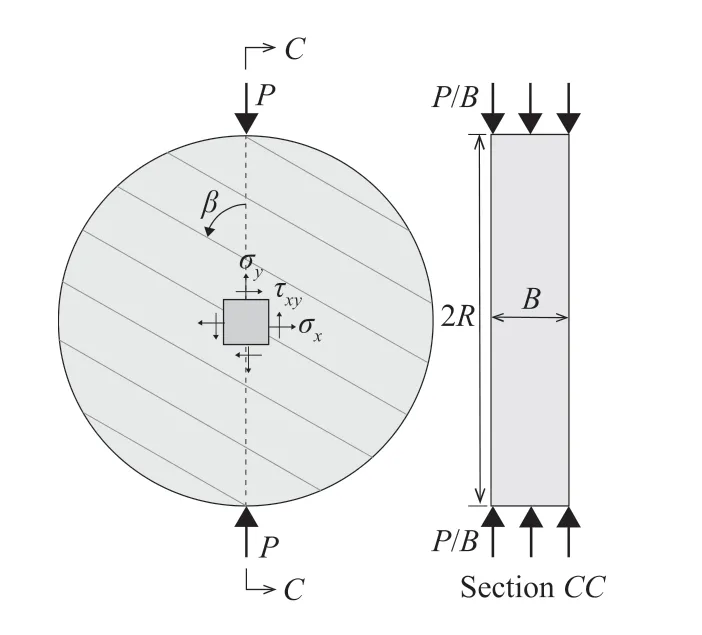
Fig.1.The BD configuration for a transversely isotropic material.β is the angle between the isotropic plane and the load axis.

Once these normalized values are obtained from the numerical or analytical methods, one can experimentally determine the stresses at the center of the disk using the corresponding load, P,and the geometrical dimensions, R and B, as

By performing a great number of FE simulations,the stresses at the center of the BD specimen were obtained for six values of the anisotropy ratio of Young’s modulus,i.e.ξ=1,1.5,2,3,4,and 5,and seven values of the material orientation, i.e.β = 0°,15°, 30°, 45°,60°,75°,and 90°.In all these simulations,the Saint-Venant relation was used to obtain the transverse shear modulus, i.e.η = 1.Then,the results were normalized based on Eq.(12) and plotted in the form of reference plots (Fig.4) which can be later used for experimentally determining the stresses from the BD test by replacing the load and geometrical dimensions in Eq.(13).The reference plots in Fig.4 represent a complete range of stresses at the disk center within the boundaries of the rock materials when the Saint-Venant relation is considered.As discussed in Section 2,η ≈1 for most of the common rocks.But if η ≠1, the effect of η must also be evaluated which will be discussed in the Discussion.

The results from the FE simulations were compared with those obtained from the analytical solution(without any simplifications)reported in Chen et al.(1998).Table 1 presents the values of ~σxobtained from both numerical and analytical methods for various β and ξ suggesting that they are in a good agreement.In other words,both numerical and analytical methods give the same results.Thus,Fig.4 can be used as a reference plot instead of both methods.

Table 1The normalized tensile stress （~σx） at the center of the transversely isotropic BD specimen: a comparison between the results from FE simulations with those obtained from the general solution when β = 0°, 30°, 60°, and 90°,ξ = 2, 3, 4, and 5,η = 1, and ν＇ = 0.1.

The contours of stresses σxand τxyfor a circular view cut of an anisotropic disk(0.7R)are illustrated in Fig.5.The simulations were performed for an anisotropic disk under a loading of P = 1 N with dimensions R=10 mm,and B=1 mm and anisotropy ratios ξ=2,and η = 1.Note that the coordinate system in Fig.5 shows the center of the undeformed disk that shifts to a new position due to the deformation.The new center of the deformed disk is specified by a white dot.On one hand, the contour of σxis elongated across loading when β is 0°or 90°, while it kinks towards the material orientation when β=45°.σxis maximum at the disk center for all cases.On the other hand, τxyis not zero at the disk center when β = 45°(τxy/σx≈0.16).

Fig.5.The evolution of stresses(σx and τxy)shown for a circular view cut from the center of the anisotropic disk obtained from FE simulations for three material orientations β=0°,45°, and 90° (ξ = 2, η = 1, P = 1 N, R = 10 mm, and B = 1 mm).The stresses are in MPa.

3.3.An approximate formula fitted to the results

Claesson and Bohloli(2002)presented an approximate formula for characterizing the normalized tensile and compressive stresses at the disk center based on the analytical solution.In this study,the normalized stresses ~σxand ~σyare obtained by re-writing the mentioned equation (Claesson and Bohloli, 2002), based on the dimensionless parameters ξ and η in addition to the material orientation β.Also, the same parameters (β, ξ, and η) are used to find an equation for the normalized shear stress~τxywhich agrees well with our FE simulation results.

Here,β＇=90°-β,and a=1.555.If the Saint-Venant assumption is considered, the value of b will be equal to zero.This means that the normalized shear stress only depends on the material orientation β and the ratio of Young’s modulus ξ.Otherwise,the effect of the ratio of shear modulus η on the shear stress must also be taken into account and the value of b is calculated as

We have recently shown that the effect of the term 2ν＇(1-η)/η on the complex roots of the characteristic equation, which characterize the in-plane stresses of an anisotropic plane, is negligible within the boundaries of the rock materials.For more details about these boundaries and conditions, refer to Aminzadeh et al.(2019).Here,a smaller term,ν＇(1-η)/η,has appeared for the stresses at the center of an anisotropic disk that may be ignored similar to that derived for the general deformation solution of an anisotropic plane.However,the induced error due to omitting the term is also evaluated for the BD in the Discussion, suggesting that both equations give almost the same results.This simplifies Eq.(14) to

Fig.4.Normalized stresses~σx,~σy,and~τxy against anisotropy ratio ξ based on Eq.(16)and FE simulations considering the Saint-Venant assumption(η=1).The results from Eqs.(14)and (16) are equal when η = 1.

where

Eq.(16)characterizes the stresses at the center of the disk based on the material orientation,β,and the two dimensionless ratios of Young’s modulus ξ = E/E＇, and the apparent shear modulus η =G＇/G＇sv.It is useful to note that the stresses in the above equation only depend on ξ,η,and β.Besides,all the stresses will only depend on ξ and β if the Saint-Venant assumption is considered.Although Eq.(16)may seem similar to that proposed by Claesson and Bohloli(2002)at the first glance,it has several important advantages apart from this simplification.The normalized stresses are formulatedbased on the dimensionless ratios of shear and Young’s moduli which have clear physical meanings and boundaries for the rock materials(1 ≤ξ ≤4 and 0.7 ≤η ≤1.3).The parameter a introduced in Claesson and Bohloli (2002) is only a mathematical formula,whereas it is converted into a combination of ξ and η in our formula,thus specific boundaries can be determined for it (0.5 ≤a ≤1.4).Moreover, defining the ratio of the shear modulus asη = G＇/G＇svsignificantly simplifies the equations in the case of using the Saint-Venant relation.Eq.(16) has the advantage of being very simple and practical,thus its outcomes will be compared with the results from the initial equation as well as the ones from the numerical simulations to evaluate its accuracy.We also fitted another formula to the numerical results with more accuracy, but we finally decided to only improve the existing formula which was in good agreement with the analytical solution.Thus,the proposed formula can be considered as a good approximation for both analytical and numerical results.

The importance of the shear stress at the center of the disk(presented in the form of an equation in this work for the first time)should not be underestimated.The simplest method to determine the elastic parameters from a BD is based on writing the stressstrain relations in x and y directions when β = 0°and 90°(Fig.1).Hence, the four unknowns (E, E＇, ν＇, and G＇) can be obtained using four equations when the load and the corresponding strains are known.Nejati et al.(2020a) used the same way to experimentally find the elastic parameters of two types of rocks and compared the results with those obtained by uniaxial compression tests.Knowing the formula for the shear stress at the center of the disk, one can also consider other material orientations to add more equations for finding the four unknowns.Let us consider one disk tested under compressive loading for β=0°,30°,60°,and 90°in a way that the behavior of the material is still mainly elastic (for example loaded between 30%-60% of the failure load).This leads to eight stressstrain equations with four unknowns i.e.an overdetermined system of equations.By increasing the number of these equations forone specimen, the influence of the heterogeneity can be reduced.This will be shown in a later work through experimental studies.

Fig.4 also shows that the results of Eqs.(14) and (16) coincide when η=1.Eq.(14),which has been shown to agree well with the results of analytical solution (Claesson and Bohloli, 2002), and its simplified form(Eq.(16))show a good agreement with the results of the FE simulations as well, except for ~σxwhen β = 75°and 90°(especially for ξ > 2).The numerical simulations of highly anisotropic materials(ξ>2)show decreasing values of~σxfor β=75°and 90°, which are different from the results of Eq.(14) since the accuracy of Eq.(14) decreases with ξ (refer to Table 1 in Claesson and Bohloli (2002)).It should be mentioned that ξ ＜2 for most common rocks.Thus for these rocks, the results of the formula which are more consistent with the simulations will be used.On the other hand,for the rocks with higher anisotropy ratios,one may prefer to use the FE results presented in Figs.4 and 6.

In general,the absolute values of ~σxand ~σy,obtained from both methods, increase with the higher values of ξ for all material orientations although some exceptions are observed in the FE results.In this study, the approximate formula fitted to the analyticalresults is proposed because of its simplicity and efficiency although more accurate numerical-based equations were formulated (especially for β=75°and 90°)for~σx,~σy,and~τxy,among which only the one for~τxywas chosen to be presented in this paper.The evaluation of the errors between numerical and analytical results will be presented in the next section.

Fig.6.Normalized stresses ~σx, ~σy, and~τxy against anisotropy ratio ξ based on Eq.(14), Eq.(16), and FE simulations when the transverse shear modulus is very far from the Saint-Venant assumption (η = 0.7 and 1.3).

4.Discussion

In this section, it is first shown how and to what extent the simplifications considered to simplify the equations of normalized stresses at the center of the BD may afect the outcomes.To achieve this,we compare the results of the complete form of the equation to those obtained from the simplified equation.Then,the consistency between the results of the formula and numerical simulations is studied.Finally, the influence of the assumption ν＇= 0.1 on the simulations is evaluated by presenting the results of several extra simulations with various ν＇values.

4.1.The negligible effect of ν＇(1 - η)/η on the normalized stresses

The results from the approximate formula fitted to the analytical results from Eq.(14)(Claesson and Bohloli,2002)are compared to those obtained from numerical simulations and simplified analytical equations in Fig.6.As described before, this equation is simplified to Eq.(16) by ignoring the term ν＇(1 -η)/η which has a small contribution due to the realistic values of ν＇and η.As can be clearly seen in Fig.6, the results of ~σxand ~σyfrom both the initial and simplified equations, i.e.Eqs.(14) and (16), are very close to each other.To compare them quantitatively, the following error measures are used to calculate the errors due to using our simplified equation instead of Eq.(14):

Table 2Average error of Eq.(16) compared to Eq.(14) (Claesson and Bohloli, 2002)(β=0°,15°,30°,45°,60°,75°,and 90°;and ξ=1,1.5,2,3,4,and 5).Refer to Eq.(18) for the error definition.

Table 3Average error of Eq.(16)compared to the results of the FE simulations(β=0°,15°,30°,45°,60°,75° and 90°;and ξ=1,1.5,2,3,4 and 5).Refer to Eq.(19)for the error definition.

Fig.7 illustrates error changes inandversus the material orientation,β,due to ignoring the term ν＇(1-η)/η when η=0.7 and 1.3 for ξ=2.The highest errors for bothand(exand ey)occur at angles 0°,45°and 90°when η=0.7 and 1.3 although the errors are always smaller when η=1.3.The highest errors for~σxand~σyare about 2%and occur at β=0°and β=45°,respectively,showing that the difference between the two equations is very small.Therefore,ignoring the term ν＇(1-η)/η will not induce considerable errors in the original formula within the boundaries of rock materials and can be applied as a useful simplification to omit the parameter ν＇from the equation.In other words,although the normalized stress is a function of four elastic parameters E, E＇, ν＇, and G＇, thecontribution of ν＇to the values of~σxand~σyis very small compared to the other three parameters.This is also confirmed by numerical simulations which will be presented in Section 4.3.

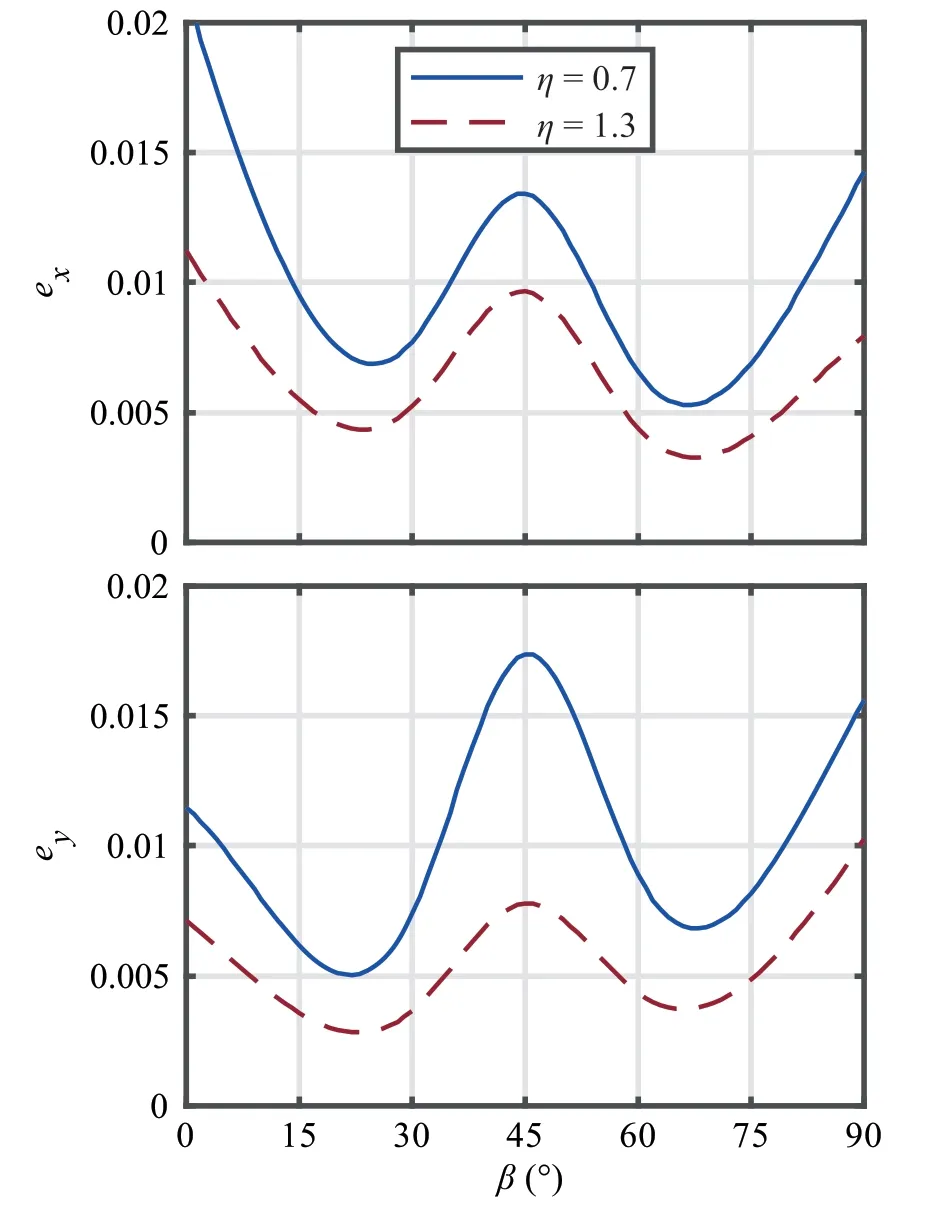
Fig.7.The errors in normalized stresses(~σx and ~σy)against the material orientation β due to omitting the term ν＇(1-η)based on Eqs.(14)and(16)for ξ=2.Refer to Eq.(18)for the error definition.

4.2.The influence of η on the normalized stresses

As previously shown in Section 2,the stresses at the disk center are functions of two dimensionless anisotropy ratios, ξ and η, in addition to the material orientation β.Besides, it was mentioned that the Saint-Venant assumption results in a realistic estimation for the G＇of various rocks.That is why η=1 can practically be used for a wide range of anisotropic rocks.It is very rare to observe a rock with an apparent shear modulus that deviates from 0.7 ＜η ＜1.3.Therefore,the two values(η=0.7 and 1.3),as the boundaries of the rock materials, are used to assess the effect of η on the values of normalized stresses.The results of the FE simulations are plotted in Fig.6 for ξ=1.5,2,3 and 4,β=0°,15°,30°,45°,60°,75°and 90°,and η = 0.7 and 1.3.The values show a significant difference of about 20%between some of the results when η increases from 0.7 to 1.3 for both analytical and numerical results of ~σxand ~σyespecially for β = 0°and 90°.For the normalized shear stress,not only the differences are very high but also the general pattern of the two plots is very different.This shows that the effect of η on the normalized stresses must be taken into account when its value deviates from the Saint-Venant assumption.

The results from the approximate formula fitted to the analytical results, i.e.Eq.(16), are also included in Fig.6.Again, our formula agrees well with the numerical results except for β = 75°and 90°with high anisotropy ratio of ξ > 2.The difference between the results of our formula and FE results is calculated as an error from the following equations:

The average errors of the normalized stresses based on Eq.(16)and FE results are calculated considering all the parameters within the range of rock materials (1 ≤ξ ≤5 and 0.7 ≤η ≤1.3) and presented in the first line of Table 3.As can be seen,the numerical and analytical results have less than 5% error for ~σxand ~σywhile they show 15% error for ~τxy.Note that this is the error bound for the entire range of parameters,however,for most of the rocks,the error will be smaller since their anisotropy ratios will not reach the considered limits.As an example, the average error of ~τxywill reduce to exy≈12%for β=0°,15°,30°,45°,60°,75°and 90°,ξ=1,1.5, 2, 3, 4 and 5, and η = 1.

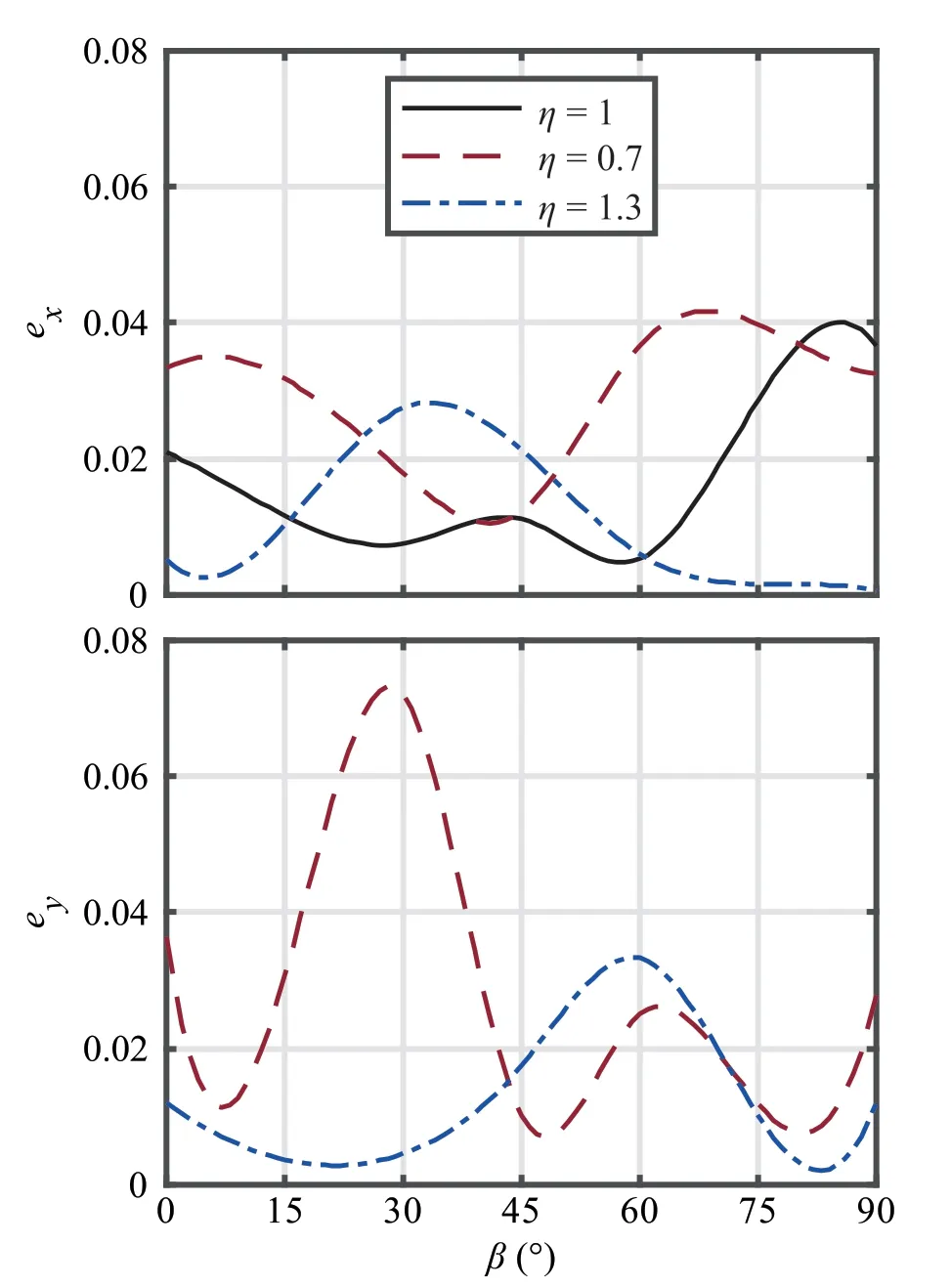
Fig.8.The errors in normalized stresses(~σx and ~σy)against the material orientation β for ξ = 2 and η = 0.7,1 and 1.3 based on analytical (Eq.(16)) and numerical results.Refer to Eq.(19) for the error definition.

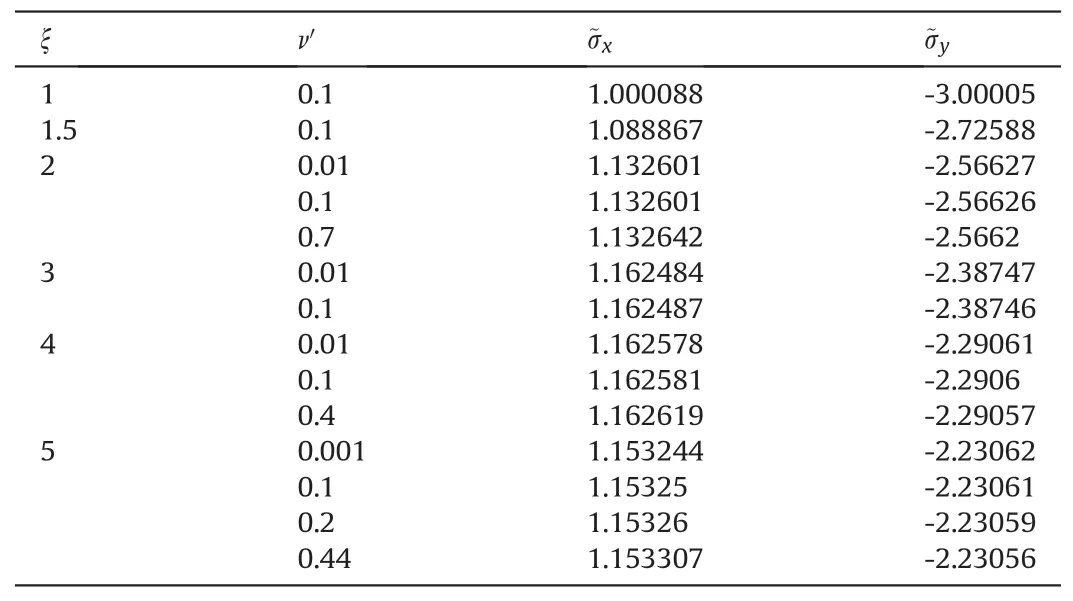
Table 4The variation of ~σx and ~σy due to the changes in the values of ν＇.The results are obtained from FE simulations of BD specimen for ξ=1,1.5,2,3,4 and 5 and β=90°.Note that some of the ν＇ values are practically impossible due to the restrictions of the elastic constants.

Fig.8 shows the variation of the errors in ~σxand ~σybased on Eq.(16)and FE results for a typical anisotropic ratio of ξ=2.As can be seen, the errors are not significant and show that the results from both numerical and analytical methods are consistent.Although our formula agrees more with the analytical results(Claesson and Bohloli, 2002), it gives acceptable results for numerical simulations with maximum errors of less than 5% and 8%for tensile and compressive stresses, respectively.The maximum error for ~σxand ~σyoccurs for η = 0.7 at β ≈70°and β ≈30°,respectively.

4.3.The small influence of the transverse Poisson’s ratio (ν＇) on the normalized stresses

As previously mentioned, the value of G＇svis calculated by assuming ν＇=0.1 in the Saint-Venant relation, i.e.1/G＇sv= 1/E+（1+ 2ν＇）/E＇.To evaluate the influence of this assumption(ν＇= 0.1)on the results of normalized stresses~σxand ~σy,various values of ν＇were used while modeling the BD specimen.In all these simulations, the material is oriented perpendicular to the loading direction, which is expected to be more critical than the parallel direction,and the ratio of the Young’s modulus increases from 1 to 5.As can be seen in Table 4, the results obtained for different transverse Poisson’s ratios show only very small deviations from those obtained for ν＇=0.1.For instance,by increasing ν＇from 0.001 to 0.44, both values of ~σxand ~σychange only 0.005% and 0.002%,respectively.Thus, it can be deduced that our assumption will not have a significant effect on the results of normalized stresses within the physical boundaries of the rock materials even if the value of ν＇deviates from 0.1.

On one hand,it was previously discussed that 0.1 ＜ν＇＜0.3 for most of the transversely isotropic rocks based on the reported experimental data in the literature.On the other hand,the values of ν and ν＇cannot exceed the thermodynamic restrictions,i.e.-[1-ν/(2ξ)]0.5＜ν＇＜[1 - ν/(2ξ)]0.5.Here, the value of ν＇is supposed to exceed this limitation only for the evaluation of its effect on the stresses although it is impossible from the physical point of view.Therefore, this high variation in the value of ν＇is impossible from both theoretical and experimental points of view and the errors in the determination of the normalized stresses will be less than what is reported here.

5.Conclusions

The normalized stresses at the center of a transversely isotropic BD specimen under compressive loading have been studiedthrough the elastic anisotropy, and the following conclusions are drawn:

(1) It is proved that the normalized stresses at the disk center are functions of material orientation and two dimensionless ratios, i.e.the ratio of Young’s modulus to the transverse Young’s modulus and the ratio of the transverse shear modulus to the Saint-Venant prediction.These parameters have specific physical meanings and boundaries for the rock materials.Moreover,if the Saint-Venant relation is used for a rock material, only the material orientation and one dimensionless parameter will be essential for characterizing the normalized stresses at the center of the disk.It is shown that the influence of Poisson’s ratio on the normalized stresses at the center of the BD specimen is very small compared to the other material properties.

(2) Based on these dimensionless definitions, an approximate formula fitted to the analytical results, previously proposed in the literature for the normalized tensile and compressive stresses, was re-written and simplified by omitting a term with a very small contribution.

(3) A great number of FE simulations are performed for anisotropic BD specimens considering various values for the two anisotropy parameters and the material orientation, and the outcomes are illustrated as reference plots forlater use.The results of numerical simulations in the reference plots agree well with the analytical solutions,which makes it applicable for various levels of anisotropy and loading orientations instead of both methods.Besides,a simple formula for the normalized shear stress is proposed based on the numerical results.

(4) The results from the simplified approximate formula fitted to the analytical results are included in the plots for comparing the two methods.The results from both analytical and numerical simulations are in good agreement, suggesting that the equation can be used as a simple and practical method to find the stresses at the center of a BD with low to moderate anisotropy.For higher levels of anisotropy,we propose to use the reference plots for higher accuracy.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This study was partially supported by the Institute of Geology of the Czech Academy of Sciences project RVO 67985831.

List of symbols

B Thickness of the disk

E, E＇Young’s moduli along and perpendicular to the material orientation, respectively

G, G＇Shear moduli along and perpendicular to the material orientation, respectively

G＇svApproximate transverse shear modulus based on the Saint-Venant assumption

P Compressive load

R Radius of the disk

ux, uyDeformations in x and y directions, respectively

x, y Cartesian coordinates

α The ratio of the Young's modulus of the disk to that of the jaw

β Angle between the material orientation and the x direction or the load line

η Dimensionless anisotropy parameter of the shear modulus, and η = G＇/G＇sv

μk,μk（k = 1， 2）Complex conjugate roots of the quartic (characteristic)equation in an arbitrary coordinate system xy

v, v＇Poisson’s ratios along and perpendicular to the material orientation, respectively

ξ Dimensionless anisotropy parameter of the Young’s modulus, and ξ = E/E＇

σ, ε Stress and strain vectors,respectively

σi, εi(i = x, y)Normal stresses and strains in an arbitrary coordinate system xy

σi, εi(i = x＇, y＇)Normal stresses and strains in the principal coordinate system xy

τij,γij(i, j = x, y)Shear stresses and strains in the principal coordinate system, xy

τij,γij(i, j = x＇, y＇)Shear stresses and strains in the principal coordinate system xy

φ Airy stress function

Φ1,Φ2, F1, F2Complex potentials