Evaluation of freezing state of sandstone using ultrasonic time-frequency characteristics

Jiwi Zhang, Julian Murton, Tim Can, Vikram Maji,d, Lili Sui, Shuji Liu,Song Zhang

a University of Science and Technology Beijing, Beijing,100083, China

b Permafrost Laboratory, Department of Geography, University of Sussex, Brighton, BN1 9QJ, UK

c Beijing Key Laboratory of Urban Underground Space Engineering, University of Science and Technology Beijing, Beijing,100083, China

d Department of Earth Sciences, Indian Institute of Technology Kanpur, Kanpur, India

e North China University of Technology, Beijing,100041, China

Keywords:Frozen sandstone Uniform freezing Upward freezing Ultrasonic testing Freezing state

ABSTRACT Common problems in engineering projects that involve artificial ground freezing of soil or rock include inadequate thickness, strength and continuity of artificial frozen walls.It is difficult to evaluate the freezing state using only a few thermometer holes at fixed positions or with other existing approaches.Here we report a novel experimental design that investigates changes in ultrasonic properties (received waveform, wave velocity Vp, wave amplitude, frequency spectrum, centroid frequency fc, kurtosis of the frequency spectrum KFS, and quality factor Q) measured during upward freezing, compared with those during uniform freezing, in order to determine the freezing state in 150 mm cubic blocks of Ardingly sandstone.Water content, porosity and density were estimated during upward freezing to ascertain water migration and changes of porosity and density at different stages.The period of receiving the wave increased substantially and coda waves changed from loose to compact during both upward and uniform freezing.The trend of increasing Vp can be divided into three stages during uniform freezing.During upward freezing, Vp increased more or less uniformly.The frequency spectrum could be used as a convenient and rapid method to identify different freezing states of sandstone(unfrozen,upward frozen,and uniformly frozen).The continuous changes in reflection coefficient rφ, refraction coefficient tφ and acoustic impedance field are the major reason for larger reflection and refraction during upward freezing compared with uniform freezing.Wave velocity Vp,wave amplitude Ah,centroid frequency fc and quality factor Q were adopted as ultrasonic parameters to evaluate quantitatively the temperature T of uniformly frozen sandstone, and their application within a radar chart is recommended.Determination of Vp provides a convenient method to evaluate the freezing state and calculate the cryofront height and frozen section thickness of upward frozen sandstone, with accuracies of 73.37%-99.23%.

1.Introduction

Artificial ground freezing (AGF) is commonly used to stabilize and seal water-bearing and unstable sandstone layers for purposes of civil and mining engineering (Andersland and Ladanyi, 2003;Pimentel et al.,2011;Vitel et al.,2015,2016).Geological factors such as groundwater seepage, faults, cavities and interbedded strata,however, may result in inadequate thickness and strength of artificial frozen walls in different parts of the ground, which can be difficult to monitor using limited numbers of temperature sensors installed at fixed positions.However, it is essential to monitor frozen wall development for evaluating the freezing state (i.e.the average temperature and cryofront(0°C isothermal)position)and ensuring the stability of excavations.

Several methods for monitoring AGF have been proposed to evaluate the frozen wall development.Real-time monitoring of temperature using thermometer holes during freezing (Dolgov,1961) is an effective approach for evaluating freezing state.Thetemperature field and its trend can be forecast by numerical simulations based on temperature monitoring obtained from field observations (Sanger and Sayles,1979; Hu et al., 2013).However,these methods analyze the ground temperature near the fixedposition thermometer holes rather than throughout the frozen wall region, and thus cannot accurately predict unfrozen gaps between two freezing pipes if the thermometer holes are far away.

One geophysical method used to determine the thickness of frozen bedrock is ground penetrating radar (GPR) (Song et al.,2013).This method utilizes the differences in dielectric constant and resistivity between unfrozen and frozen soils.GPR profiles,however, are influenced by freezing pipes made of steel and are subjected to a detection depth of only ～3-30 m, which can limit their applicability.The dielectric constant of steel is far higher than that of frozen and unfrozen soils, leading to image penumbra.Therefore,GPR is now rarely used in AGF in the field.

A second important geophysical parameter used to distinguish frozen and unfrozen soils or rocks in field conditions is wave velocity (Hauck, 2001).Accordingly, seismic refraction tomography(SRT) has been widely used in permafrost to identify frozen and unfrozen bedrocks (Swanger et al., 2010; Ramachandran et al.,2011; Sadurtdinov et al., 2012).However, some factors associated with AGF,such as number of steel freezing pipes(usually more than 20 in total),large frozen depths(commonly 20-600 m),and rapid advance of freezing boundaries (usually 20-40 mm/d), mean that this method cannot meet the required accuracy in deeply frozen ground for monitoring artificial frozen walls,except possibly during early stages of freezing (see Section 4.2).

A third effective technique to detect wave velocity of frozen and unfrozen soils or rocks is ultrasonic testing (UT).Compared with SRT, ultrasonic emission and reception sensors can be placed within any two freezing pipes and are little affected by the steel pipes, deeply frozen ground and rapid movement of freezing boundaries.Therefore,UTcan provide accurate acoustic parameters between any two freezing pipes and is more suitable than SRT for evaluating frozen wall development during AGF.

Several previous laboratory studies have used ultrasonic methods to investigate the relationships between P-wave properties (i.e.wave velocity and attenuation) obtained by UT and physico-mechanical properties of different rocks.Chary et al.(2006) investigated the correlation between ultrasonic pulse velocity and engineering properties of sandstones and used the ultrasonic method to evaluate their elasticity.Chaki et al.(2008)evaluated the overall porosity, orientation and size of microcracks in granite by the wave velocity.Korobiichuk (2016) established an expression relating the wave velocity with temperature (15°C to -25°C) for Mezhdurechenskiy granite, and found that the velocity of elastic waves changed significantly as temperature decreased from 0°C to -20°C.Dou et al.(2016) established an effective medium model based on ultrasonic P-wave data.These studies, however, focused on the change of wave velocity and attenuation of unfrozen or uniformly frozen rock at different temperatures.The ultrasonic time-frequency characteristics (i.e.received waveform, wave velocity Vp, head wave amplitude Ah,frequency spectrum, centroid frequency fc, kurtosis of the frequency spectrum KFS,and quality factor Q)of saturated sandstone during uniform and progressive upward freezing have not been investigated systematically, and thus the mechanical understanding of involved processes is lacking.This knowledge gap is a major obstacle for utilizing multiple acoustic parameters to evaluate the freezing state of frozen walls during AGF.

The aim of the present study is to evaluate the freezing state of sandstone blocks by UT under two different types of controlled laboratory conditions.The objectives are to describe and interpret the results concerning the changes of acoustic parameters during laboratory experiments involving progressive upward and uniform freezing of the blocks at spatially regular but progressively lower temperatures.Uniformly frozen sandstone blocks were tested at different positive and negative temperatures in order to investigate the relationships between acoustic parameters (i.e.received waveform, Vp, Ah, frequency spectrum, fc, KFS and Q) and temperature.The ultrasonic properties of sandstone were also measured during upward freezing conditions in order to simulate artificial frozen wall development near the frozen wall boundary, and to study the relationships between acoustic parameters and cyrofront position.Some physical parameters (water content, porosity and density) were estimated for different stages of upward freezing to determine water migration and changes in porosity and density.The mechanisms of changes in ultrasonic parameters during upward freezing are proposed.Overall, the present study provides a novel method for evaluating the freezing state of frozen sandstone,and builds upon our previous study on freezing of remolded homogeneous fine sand (Zhang et al., 2021a).

2.Materials and methods

2.1.Experimental design

The present study focuses on rock rather than remolded soil because we seek to investigate UT characteristics of a cemented material that is internally variable because of natural geological features(stratification).Such variability is more similar to the field situation of artificial freezing of stratified sedimentary rocks such as sandstones rather than freezing of remolded soils.The rock type used in the experiments was Ardingly sandstone,a rock type used in the laboratories of University of Sussex, UK, during previous experiments on frost weathering(Williams and Robinson,2001).In terms of its visible physical properties,the rock is fine-to mediumgrained, poorly cemented and well laminated.Samples were obtained from one of the two Masonry “lifts” (beds) of the Ardingly Sandstone Member of the Tunbridge Wells Sand Formation(Radley and Allen 2012)at Philpots Quarry,West Hoathly,West Sussex,UK.

The physical properties of the sandstone measured in the Permafrost Laboratory at the University of Sussex, UK, included bulk density(1.99-2.3 g/cm3),saturated gravimetric water content(8.01%-10.46%)，and porosity (20.44%-25.38%).The bulk density and water content were measured according to ASTM D5550-14(2014) and ASTM D698-12(2021) (2021), respectively.The porosity φ (in %) was estimated, after drying the rock, as follows:

where ρdis the dry density of the sample (g/cm3); and ρpis the particle density (g/cm3), and is assumed to be equal to that of quartz (2.65 g/cm3), which is the main mineral of sandstone.

The experiments were performed in the Permafrost Laboratory according to two experimental designs:(1)upward freezing and(2)uniform freezing at different temperatures (hereafter termed as uniform freezing experiment).

The upward freezing experiment was carried out in a cold room.As shown in Fig.1, the blocks were placed on a basal cold plate(manufactured by Freezertech, Humberston, UK).The plate was rectangular (with dimensions of 1500 mm × 600 mm × 50 mm)and was chilled by gas circulating within it.The plate was controlled thermostatically to maintain a mean user-controlled freezing temperature beneath the blocks.The plate thermostat was set to -20°C, the average temperature at which lowtemperature refrigerant is commonly used in AGF.At intervals during upward freezing of the blocks, the time and frequency-domain characteristics of partially frozen rock were measured as the cryofront (0°C isotherm) rose to heights of 30 mm, 60 mm,90 mm,120 mm and 150 mm (Fig.1).

Fig.1.Experimental design of upward freezing experiment.Units are in mm.Block 1 shows cryofront at 30 mm, block 2 at 60 mm, and block 5 at 150 mm.Blocks 3 and 4 are omitted for clarity.Block 6 shows height of temperature sensors above the base of the block.

The uniform freezing experiment was carried out in a climate cabinet (ECO 400 climate cabinet manufactured by Temperature Applied Science Ltd., UK).The aim of this experiment was to measure acoustic parameters of sandstone at 10 different temperatures (20°C, 5°C,1°C, 0°C, -1°C, -3°C, -5°C, -10°C, -15°C,and -20°C) that were maintained (until acoustic measurement was completed) in a steady-state and spatially uniform condition throughout the blocks.In other words, the temperature field was uniform and unchanged throughout each block at the time of measurement.Then the temperature was lowered to the next value in the series and the acoustic parameters were re-measured(MT/T 593.8-2011, 2011).Finally, the acoustic parameters measured at different temperatures were compared with those measured in the upward freezing experiment.

2.2.Sample preparation

Eighteen cubic samples of 150 mm × 150 mm × 150 mm were obtained from sandstone blocks.The samples were oven-dried at a temperature of 40°C(to avoid temperature-induced microcracking during drying at higher temperatures)for about 7 d until their dry weight was constant.Then, all of the dry samples were measured by UT to select nine for further testing.Samples were selected on the basis that their wave velocity in the direction parallel(face A to C or B to D in Fig.1)or perpendicular(from top to bottom,Fig.1)to primary stratification was similar in value.Next,the basal ～30 mm of the nine sample blocks was submerged in a water-filled container for 3 d to wet the samples by capillary rise and thus displace air from the rock pores.Then the samples were completely submerged in water to saturate them fully, as determined by measuring their wet weight at intervals until it was constant(afterabout 5 d).Next,the saturated samples were wrapped in cling film to restrict migration of liquid water into or out of the samples during upward and uniform freezing.Finally, all the saturated samples were measured by UT to determine their acoustic parameters.Blocks 1-6 were placed on the cling film laid directly on top of the basal cooling plate(Fig.1).

The nine samples were selected for different purposes(Table 1).Blocks 1-6 were tested in the cold room for the upward freezing experiment,whereas blocks 7-9 were tested in the climate cabinet for the uniform freezing experiment.In addition, blocks 1-5 were used for measuring physical (water migration, density and porosity) and acoustic parameters when the cryofront arrived at heights of 30 mm, 60 mm, 90 mm,120 mm and 150 mm (Fig.1).Therefore, blocks 1-5 were frozen upward at the same time and taken off the basal cold plate at intervals, when the ascending cryofront arrived at each target height.Then the physical parameters(water content,density and porosity)and acoustic parameters of the partially frozen blocks were determined.Block 6 was remained on the cooling plate throughout the upward freezing experiment in order to measure rock temperature.During a repeated upward freezing experiment, block 6 was thawed completely and saturated again,and then placed back onto the cold plate to perform UT again when the cryofront arrived at successive,specified heights, so that the acoustic parameters could be rechecked.

Table 1Measurements for samples.

2.3.Monitoring strategy

2.3.1.Upward freezing experiment

In the upward freezing experiment, we measured rock weight,volume,temperature and acoustic parameters at different heights of the cryofront as it ascended through the sandstone samples.The weight and volume of samples were measured by a high-precision electronic balance and a vernier caliper, respectively, to calculate the water content, porosity and density at different heights during upward freezing.Therefore,it was necessary to weigh and measure the volume of blocks 1-5 in sequence during upward freezing(Fig.2).Before freezing,samples 1-5 were cut with a rock saw to produce a 30-mm-thick vertical subsample, leaving the remainder of each sample to be 120 mm×150 mm×150 mm(wide×long×high)for the upward freezing experiment.Then, the 30-mm-thick vertical subsample was sawed into five 30-mm-thick horizontal slices to measure the initial physical parameters(water content,density and porosity) at different heights.The volume of subsample was measured by a digital caliper with a resolution of 0.01 mm.During upward freezing, samples 1-5 were taken off the cold plate in sequence when the cryofront arrived at specified heights(30 mm in block 1,60 mm in block 2,90 mm in block 3,120 mm in block 4,and 150 mm in block 5).Then,the extracted block was cut into five 30-mm-thick horizontal slices immediately(within about 5-10 min after taking it off the cooling plate)in order to measure the weight and volume of each slice.Afterwards, each horizontal slice was dried at 40°C for about 7 d in an oven until its dry weight was constant,and then reweighed.After that,the volume was re-measured.Finally,the moisture content, density and porosity of the rock at five specified heights of the cryofront (30 mm, 60 mm, 90 mm, 120 mm, and 150 mm)were calculated according to Section 2.1.

The temperature of block 6 during upward freezing was measured by seven cylindrical platinum resistance thermometers(Pt100).The temperature sensors were first immersed in an icewater bath to calibrate to an accuracy of ±0.1°C, and then embedded in horizontal holes of block 6 at heights of 30 mm,60 mm, 90 mm,120 mm, and 150 mm above the base (Fig.1) to measure temperature change and determine cryofront position during upward freezing.Temperature sensors were also placed beneath the block (0 mm height) and directly on top of the basal cold plate away from the block.Temperature data from multiple Pt100s were recorded and its profile was displayed using a multiplexed USB data acquisition system (model cDAQ-9172-NI) manufactured by the National Instruments, USA.The data acquisition system and voltage to temperature conversion were designed using the virtual interface (VI) of LabVIEW software.The sampling frequency was 2.5 kHz and the mean values were considered for projecting in the graphical interface and recorded for further analysis.

Acoustic parameters before and after upward freezing were measured using a non-metal NM-4A ultrasonic tester (manufactured by the KangKeRui Ultrasonic Engineering Co.,Ltd.,China).In view of the anisotropy (stratification) of the sandstone, we measured acoustic parameters (P-wave velocity, amplitude and frequency spectrum) of each block in the directions parallel to the stratification (face A to C, and B to D) at different heights (around 30 mm,75 mm and 120 mm)and perpendicular to the stratification(from top to bottom) (Fig.3).In this way, the changes of acoustic parameters at the same location before and after upward freezing were calculated.

2.3.2.Uniform freezing experiment

The uniform freezing experiment involved monitoring ultrasonic parameters at 10 successively decreased temperatures(20°C,5°C,1°C,0°C,-1°C,-3°C,-5°C,-10°C,-15°C and-20°C).To obtain each temperature, samples 7-9 were placed inside theclimate cabinet, and the internal air temperature was set at the specified temperature for 48 h,allowing the samples to equilibrate throughout at this temperature (Fig.4a).Then the samples were taken out of the cabinet, their acoustic properties were measured immediately at the specified temperature before the samples were put into the cabinet again, and the internal air temperature was lowered to the next specified value (Fig.4b).

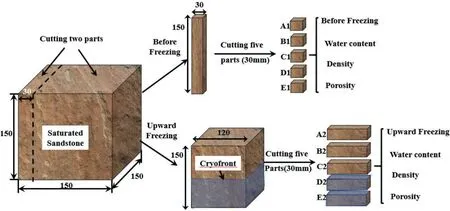
Fig.2.Experimental design for weight and volume measurement of upward freezing experiment.Units are in mm.Brown color indicates unfrozen rock, and gray color indicates frozen rock.

2.3.3.Ultrasonic test procedure

The ultrasonic test during freezing was performed in four steps.First,before measurements,the ultrasonic apparatus was calibrated according to the Chinese standard JB/T 8428-2015 (2015).Any air pockets between the block and ultrasonic transducers were eliminated by a thin film of petroleum jelly.Then,emission and receiving transducers were arranged during upward and uniform freezing experiments as per Figs.3 and 4b,respectively.Finally,the acoustic parameters of both experiments were recorded, and the P-wave velocity, head wave amplitude and frequency spectrum were calculated based on ultrasonic theories (Yang et al.,1997; Ottosen et al., 2004; JB/T 8428-2015, 2015).

2.4.Experimental system and procedure

The two experiments used the non-metal ultrasonic detector(NM-4A).As described by Zhang et al.(2020, 2021a) for experiments on fine sand, this sensor is consisted of four units: (1) an emission transducer and a receiving transducer, (2) a pulsereceiver, (3) a data acquisition system, and (4) a 5-m-long wire.The waveform of the excitation is a sine wave.The system parameters are as follows:launch voltage range=250-1000 V,frequency of P-wave transducer=100 kHz,measurement accuracy of soundintervals = ±0.05 μs, receiver sensitivity ≤10 μV, and amplitude range=0-177 dB.For both experiments,the sampling interval was 0.4 μs and the launch voltage is 500 V.

The flowchart for the experiment procedure is depicted in Fig.5,mainly including nine stages.Stages 1,2 and 9 are common to both experiments,whereas stages 3-6 refer only to the upward freezing experiment, and stages 7 and 8 refer only to the uniform freezing experiment.

2.5.Ultrasonic parameters

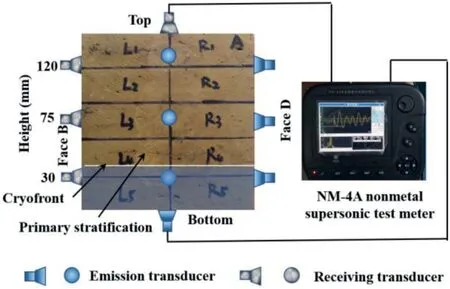
Fig.3.Experimental design for ultrasonic transducer arrangement of upward freezing experiment.Units are in mm.

In this study, we determined six main ultrasonic parameters:wave velocity Vp, wave amplitude, frequency spectrum, centroid frequency fc, the kurtosis of the frequency spectrum KFS, and the quality factor Q.The P-wave velocity measured in the laboratory can indicate the physical properties of frozen rock (Dzhurik and Leshchikov,1973; Pandit and King,1979; Remy et al.,1994; Wang et al., 2006; Sondergeld and Rai, 2007; Christ and Park, 2009;Huang et al.,2015;Zhang et al.,2020,2021a,b).The P-wave velocity Vp(in km/s) is expressed as follows:

where L is the sample length (mm), tpindicates the travel time of the head wave in the block (μs), and t0is the inherent time delay(μs).

The head wave refers to the first wave detected by the receiving transducer,and its amplitude (Ah)indicates the energy magnitude of the received wave and can be recorded by a data acquisition system (Wang et al., 2017).The variation in the head wave amplitude can be used as an effective means to estimate some evolving physical parameters in the material, including the void ratio,compaction and normal stress(Inci,2000; Kawaguchi et al.,2001;Gheibi and Hedayat, 2018).

The waveform of the received ultrasonic waves was converted from the time-domain into the frequency-domain by the fast Fourier transform (FFT) (Cote and Fox,1988; Alleyne and Cawley,1992; Ito and Uomoto, 1997; Lee et al., 2004; Hola et al., 2011).The frequency spectrum can often be used as an effective way to interpret the variation in the volume and processes of deformation or micro-fracture in rock (Wang et al., 2015a, 2017; Kong et al.,2016).

The values of the centroid frequency(fc)and the kurtosis of the frequency spectrum(KFS)were analyzed(Wang et al.,2015a,2017)after the time-domain was converted into the frequency-domain by FFT.The value of fccan be used to evaluate quantitatively the centroid point of the frequency spectrum:the higher the frequency components of P-waves attenuated,the lower the value of fc(Quan and Harris, 1997; Matsushima et al., 2016).The value of KFS indicates the “peakedness” of the frequency spectrum: the more regular and single-peaked a distribution is,the higher the value of KFS (Wang et al., 2015a, 2017).The two frequency indicators are calculated as follows:

where fiand fpare the values of discrete and peak frequencies(kHz), respectively; PAiis the proportion of discrete frequency amplitude; and Δf is the frequency difference between adjacent frequencies (kHz).

The quality factor Q provides an effective index for representing the attenuation of ultrasonic wave energy.The lower the Q value,the higher the wave energy loss (Mavko and Nur,1979), which is expressed as (Yang et al., 2021):

where f is the frequency of ultrasonic waves (kHz), and v is the phase velocity that is approximated by the P-wave velocity in this study (km/s).The attenuation coefficient, α, is calculated by measuring the decline of head wave amplitude that has passed through a known distance of material, which is expressed as(McClements,2006):

Fig.4.Experimental design for uniform freezing experiment.Units are in mm.Gray color indicates frozen rock.

Fig.5.Flowchart showing the procedure of both experiments.

where A0is the initial amplitude of the ultrasonic wave(x=0),and Axis the amplitude after it has traveled a distance x.

3.Results and analysis

3.1.Changing physical parameters during upward freezing

3.1.1.Temperature

In the upward freezing experiment, samples 1-6 were frozen from the bottom upward, driven by the basal cooling plate.The change of temperature in the instrumented sample 6 and on the top of the cold plate during upward freezing is shown in Fig.6.The temperature of block 6 was assumed to be similar to that in samples 1-5, as they all experienced the same basal cooling.The temperature of the cold plate generally varied between-16°C and-25°C(average value = -20.3°C, standard deviation = 3.05°C) during upward freezing, meeting the typical temperature boundary conditions of AGF.As the cryofront rose through sample 6, the rock temperature decreased sharply in 0-0.5 h, and then more slowly between 0.5 h and 4.8 h.The rate of temperature decrease and the temperature difference between the bottom and top of the sample 6 dropped gradually during the experiment, which indicates that the heat exchange between the cold plate and the rock was very intense during early stages of freezing.The average temperature ofsample 6 was about -10°C when the cryofront rose through the block, which was similar to that of frozen walls produced by AFG.

3.1.2.Water content

The changes of water content(Δω)in vertical profiles of samples 1-5 during upward freezing are shown in Fig.7a.Δω was expressed relative to the vertical profiles that were initially uniform in initial water contents(0%in Fig.7a)at different heights during five stages of upward freezing.Overall,unfrozen pore water tended to migrate from unfrozen towards frozen sections of rock.

Four evolving regions in the sandstone samples can be distinguished in terms of state(frozen or unfrozen)and changes in water content (increased or decreased).From top to bottom of the samples,the following regions distribute(Fig.7b):(1)Unfrozen region with decreased water content.In this region, some pore water(about 0.1%-0.5%) moved towards the rising freezing front and,presumably,was replaced by air and/or water vapor.The region was 5-60 mm high and it would have disappeared as the freezing continued until the temperature dropped below-1°C at the top of the sample block.(2)Frozen region with decreased water content.This region(～30 mm high)emerged when the cryofront had risen into the upper half of the samples during upward freezing.(3)Unfrozen region with increased water content.This region gradually decreased in thickness as the cryofront ascended from 30 mm to 90 mm height during upward freezing.(4) Frozen region with increased water content.This region was located in the lower part of the samples,and the water content in this region increased(0%-0.9%)as the distance to the cold plate decreased.The height of the region continuously increased during the early stage of upward freezing until the cryofront arrived at 90 mm, and then it was relatively stable at around 90 mm.

3.1.3.Changes in dry density and porosity

Changes in dry density (Δρ) and porosity (Δφ) in the upward freezing experiment had mean values varying from(-0.032±0.003)g/cm3to (0.059 ± 0.003) g/cm3and -2.223% ± 0.108% to 1.193% ± 0.125%, respectively (Fig.8).Most values of dry density at different heights tended to decrease slightly in frozen sections(about (-0.01 ± 0.008) g/cm3to (-0.032 ± 0.003) g/cm3) and increase in unfrozen sections (about (0.003 ± 0.004) g/cm3to(0.059±0.003)g/cm3).In contrast,the porosity modestly increased in frozen sections (about 0.382% ± 0.296% to 1.193% ± 0.125%) and decreased in unfrozen sections (about -0.122% ± 0.132%to-2.223%± 0.108%),a pattern that is inversely opposite to that of dry density.

Fig.6.Temperature change of sandstone sample 6 during upward freezing.

3.2.Ultrasonic time-domain characteristics

3.2.1.Changes in received waveform

In general, the received ultrasonic waves show a spindle waveform when the waves propagate in isotropic materials (He et al., 2007; Planès and Larose, 2013; Wang et al., 2017), but wave period reduction and messy received waves will emerge due to microcracks, larger pores and defects in sandstone that lead to reflection, refraction and diffraction of ultrasonic waves.

In our experiments, during uniform freezing, the variation of waveform at different negative temperatures was similar to that of upward freezing(Fig.9a).Messy and loose received waves appeared at-1°C and-3°C,changing into received compact waves of similar waveform as the temperature decreased from-5°C to-15°C.This demonstrates that ice crystals were negligible and unfrozen water content was abundant between -1°C and -3°C, and that ice crystals filled most of the sandstone pores and stiffened the framework as the temperature decreased below-5°C.

During upward freezing, the period of the received wave increased from bottom to top (i.e.4 periods at 0 mm, 30 mm, and 60 mm,6 periods at 90 mm and 120 mm,and 7 periods at 150 mm).In addition, coda waves (i.e.late wave arrivals of reduced amplitude)(Planès and Larose 2013)changed from loose to compact after the cryofront arrived at 60 mm height(Fig.9b).This indicates that P-wave attenuation during wave transmission became weak after the frozen section proportion exceeded 40%.In unfrozen region 1,air or water vapor replacing pore water that moved towards the freezing front (Fig.7b) caused the ultrasonic propagation path to become complex and circuitous, which was considered to have increased P-wave attenuation (Matsushima et al., 2016).However,when the cryofront exceeded 90 mm height, most pores were frozen and the unfrozen water content could almost be ignored as ice crystals grew in frozen region 4.At this time, region 4 was probably largely frozen, such that the ice matrix increased the number of connections and stiffened the region, in turn favoring lower P-wave attenuation and higher wave energy.

Overall, during earlier stages of upward freezing, a low wave period and loose waveform emerged, because the increased function of wave energy in the frozen region 4 was negligible relative to the greater P-wave attenuation in the unfrozen region 1 of decreased water content (Section 3.1.2.) before the cryofront reached 90 mm.The increased function of wave energy in the frozen region became more distinct gradually as the height of frozen region 4 increased when the cryofront arrived at 90-150 mm.

3.2.2.Changes in wave velocity

In the uniform freezing experiment, Vpincreased marginally from 2.12 km/s to 2.27 km/s as temperature decreased from 20°C to -1°C, and then increased substantially from 2.27 km/s to 4.37 km/s as the temperature continued to fall between -1°C and -5°C (Fig.10).Further cooling below -5°C led to a much slower rate of increasing Vpto a maximum value of 4.68 km/s at-20°C.The main reason for this behavior is that the equilibrium freezing point of sandstone is lower than -1°C.At lower temperatures,part of the unfrozen water changed into ice,with ice crystals filling the pores gradually when the temperature fell below the freezing point, leading to rapid increases in wave velocity.This phenomenon was also found by Nakano et al.(1972) and King(1977).As the temperature dropped from -10°C to -20°C, the wave velocity increased slowly when most of the pores in the frozen sandstone were filled with ice crystals and the unfrozen water content was negligible (Wassermann et al., 2009; Eslami et al., 2010; Heap et al., 2010).

Fig.7.Water migration during upward freezing: (a) Vertical profiles of water content changing through sample blocks 1-5 when the cryofront reaches different heights; and (b)Change in height of four evolving regions during upward freezing.

Fig.8.Changes in dry density and porosity during upward freezing: Vertical profiles of (a) dry density and (b) porosity within sandstone samples when the cryofront reaches different heights.

Fig.9.Received waveform of sandstone samples:(a)Uniform freezing at different temperatures(-1 °C,-3 °C,-5 °C,-10 °C and-15 °C),where the vertical red lines indicate the arrival time of the head wave; and (b) Upward freezing as the cryofront reaches different heights (0 mm, 30 mm, 60 mm, 90 mm,120 mm and 150 mm).

Changes in P-wave velocity during upward freezing were totally different from those in uniform freezing.Vpincreased at a more or less uniform rate as the cryofront rose from the bottom to the top of the sample blocks, because porosity in the unfrozen section continuously decreased (Section 3.1.3.) and ice crystals gradually formed and infilled pores within frozen sections(regions 2 and 4 inFig.7),leading to less P-wave attenuation and higher received wave energy in the sample.This indicates that changes of P-wave velocity can show the position of the cryofront during upward freezing.Furthermore, before the cryofront arrived at 150 mm height, Pwave velocity during upward freezing was less than that during uniform freezing at different temperatures (i.e.from -5°C to -20°C).One possible reason for this behavior is P-wave attenuation due to scattering of sandstone porosity and density variations during upward freezing(Matsushima et al.,2016).Another is more complex wave propagation in four regions and less stiffness during upward freezing.

Overall,the different trends of increasing wave velocity between uniform and upward freezing demonstrate that wave velocity change of rock at different temperatures can be used directly to evaluate the average temperature of a frozen wall between any two freezing holes during AGF.In addition,wave velocity change during progressive upward freezing can reveal cryofront height, which implies that it can also be used as an effective means to locate the artificial frozen wall boundary.

3.2.3.Changes in head wave amplitude

The head wave amplitude during upward and uniform freezing is shown in Fig.11.In the uniform freezing experiment, the head wave amplitude decreased as the temperature dropped from 20°C to 0°C, whereas the amplitude increased continuously as the temperature dropped from 0°C to -15°C.Below -15°C, the amplitude decreased again, though its absolute values exceeded the initial values.The above three stages of variation can be explained as follows: (1) Water redistribution resulted in an inhomogeneous porosity distribution as temperature fell from 20°C to 0°C,leading to more P-wave attenuation.(2)The increase of the ice volume within the samples resulted in an increased contact area between the mineral grains as the temperature dropped from 0°C to -15°C.(3) When the temperature was -20°C, new complex stochastic interfaces such as pores, contact area and microcracks led to more scattering attenuation and diffraction or refraction propagation of ultrasonic waves (Sams et al., 1997; Wang et al.,2015a).

Changes in head wave amplitude during upward freezing showed some similarity to those associated with uniform freezing.The head wave amplitude decreased as the cryofront ascended between heights of 0 and 30 mm,whereas the amplitude increased gradually as the cryofront arrived at heights of 30-150 mm.At the end of the experiment,the absolute values of head wave amplitude greatly exceeded the initial values, because some water migrated downward in the unfrozen region 1, resulting in more air and/or water vapor between mineral grains, in turn leading to more Pwave attenuation and complex wave propagation in regions 1, 2 and 4 before the cryofront reached 30 mm.However,the porosity of unfrozen region 1 decreased and ice crystals filled up the pores gradually in regions 2 and 4(Fig.7b)as the cryofront continuously rose, resulting in new contact areas and higher stiffness.

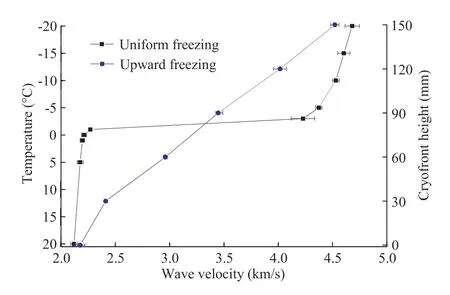
Fig.10.Vp of sandstone during upward and uniform freezing experiments.Error bars indicate standard deviation of samples 1-5 (blue) and 7-9 (black).

Fig.11.Head wave amplitude of sandstone during upward and uniform freezing experiments.Error bars indicate standard deviation of samples 1-5 (blue) and 7-9(black).

In summary, the irregular variation of head wave amplitude during uniform and upward freezing suggests that the head wave amplitude is suitable for determining the average temperature of uniformly frozen rock within 0°C to -15°C, and evaluating the cryofront height at the later upward freezing period(90-150 mm).

3.3.Ultrasonic frequency-domain characteristics

3.3.1.Changes in frequency spectrum

Wavelet transform is an effective method to eliminate highfrequency noise components of non-stable and transient ultrasonic waves (Rinkevich and Perov, 2005; Ni et al., 2008).In the present experiment, the received ultrasonic waves were disassembled into five levels by db5 wavelet to reconstruct an effective wave.Then the received wave frequency spectrum of the sandstone samples was obtained by FFT,with the cutoff frequency of 100 kHz (Section 2.4), as summarized in Fig.12.

During the uniform freezing experiment, the frequency spectrum was characterized by an irregular and multi-peaked morphology before the samples were frozen at -1°C, because ultrasonic waves passed though different layers (stratification) and three phases (rock matrix, liquid water, and air) in the sandstone(Fig.12a).The frequency spectrum gradually became more regular and single-peak as the temperature decreased, until it remained unchanged at -10°C to -15°C, when most of the pores in the frozen sandstone were filled with ice crystals and the unfrozen water content was negligible.The dominant frequency (29.64-44.4 kHz)within the temperature range of-3°C to-15°C can be considered the frequency of sandstone that is well frozen, and the frequency value increased as the temperature decreased.

During upward freezing, changes in frequency spectrum were quite different from those associated with uniform freezing(Fig.12b).The morphology of the frequency spectrum was also irregular and multi-peaked before upward freezing,and contained three frequency peaks, which may indicate three phases (matrix,liquid water,and air)in the sandstone.The early stages of freezing(0-60 mm height) were irregular and multi-peaked, with a morphology similar to that of unfrozen block, which showedmultiple frequency peaks and contained two lower frequency values (2.08-4.92 kHz and 9.8-14.6 kHz).The multi-peaked frequency increased as the cryofront height rose during later stages(60-120 mm height) until the higher frequency of three regions(labeled‘1’,‘2’and‘3’in Fig.12b)was achieved,when the cryofront arrived at the top of sample blocks (150 mm).

Fig.12.Received wave frequency spectrum of sandstone samples:(a)Uniform freezing at temperatures of-1 °C,-3 °C,-5 °C,-10 °C and-15 °C;and(b)Upward freezing as the cryofront reaches different heights (0 mm, 30 mm, 60 mm, 90 mm,120 mm and 150 mm).

The lowest frequency value (26.8-29.3 kHz) - labeled ‘1’ in Fig.12b-is less than that of saturated unfrozen matrix in sandstone(34.3-36.8 kHz).It can be regarded as the frequency of region 1(unfrozen region with decreased water content,see Fig.7b).In this region, the frequency value decreased as water migrated downwards continuously.

Intermediate frequency values (34.19 kHz) - ‘2’ in Fig.12b -appeared when the cryofront reached 150 mm.This finding indicates that the higher frequency components were absorbed before the cryofront reached 150 mm in regions 1 and 3 (Fig.7b)due to P-wave attenuation, and then they developed gradually as the height of unfrozen regions 1 and 3 decreased.The intermediate values can be considered as the frequency of region 2(frozen region with decreased water content, see Fig.7b).

The highest frequency components (43.87-46 kHz) - ‘3’ in Fig.12b - appeared after the cryofront arrived at 90 mm height.This indicates that the highest frequency components were also absorbed by unfrozen regions 1 and 3(Fig.7b),because the height of region 4 (frozen region with increased water content) was too short during early stages of freezing.The frequency range of 43.87-46 kHz is close to that of uniformly frozen sandstone within the temperature range of -5°C to-15°C.

In summary, the frequency components can obviously determine the average temperature of uniformly frozen rock by dominant frequency,and reveal the frequency of different regions due to water migration and phase change during upward freezing (Kong et al., 2014).

3.3.2.Changes in fcand KFS

In order to clarify the ultrasonic frequency-domain characteristics of sandstone subjected to upward freezing compared to those during uniform freezing, fcand KFS were calculated by Eq.(3).

As shown in Fig.13, during uniform freezing, the value of fcincreased significantly as temperature decreased from -1°C to -10°C and then increased slightly as temperature dropped to-15°C.The main reason for this behavior is that the value of fcis increased gradually as higher frequency components of P-waves increased.In contrast, the value of KFS increased substantially from -1°C to -5°C and reached the maximum value, and then dropped sharply with reduced temperature from-5°C to-15°C.Obviously,fcseems to be more suitable than KFS for evaluating the temperature of frozen sandstone.

During upward freezing, the value of fcfluctuated within a narrow range of 25-32 kHz as the cryofront height increased.The value of KFS increased significantly and reached the peak at 6.1 when the cryofront reached 60 mm,and then decreased gradually as the cryofront moved to the top of the sample.Therefore,neither fcnor KFS can be used as an effective way to evaluate the freezing state of upward frozen sandstone.

3.4.Changes in quality factor Q

The quality factor Q,an integrated parameter,can represent the attenuation of ultrasonic wave energy during wave propagation,which can be calculated by Eqs.(4) and (5).

As shown in Fig.14, during uniform freezing, the change of quality factor Q with the falling temperature for samples 7-9 can be categorized into three stages.The value of Q increased slightly at temperatures of 20°C to -1°C, and then sharply increased as temperature dropped to -15°C.Subsequently, the value of Q decreased again as the temperature dropped from -15°C to-20°C,though its absolute values far exceeded the initial values.

During upward freezing,the value of Q increased slightly as the cryofront ascended between heights of 0 and 30 mm, and peaked when the cryofront reached 60 mm.Then the value of Q decreased significantly and fluctuated within a range of 13.66-15.06.

Therefore, the quality factor Q can obviously determine the average temperature of uniformly frozen rock within -1°C to -15°C, rather than upward frozen sandstone.

4.Discussion

4.1.Consolidation in unfrozen regions during upward freezing

Consolidation may explain the increased density and decreased porosity in unfrozen regions during upward freezing, when the cryofront rose (Fig.8).Consolidation is attributed to migration of unfrozen water from unfrozen to frozen sections due to temperature gradient-induced suction, leading to consolidation of rock volume from which water was supplied (Prick, 1995; Thomachot and Matsuoka, 2007; Murton et al., 2016).However, the changes of dry density and porosity during upward freezing were smallerthan those induced by freeze-thaw cycles in saturated soils(Chamberlain and Gow,1979; Dawson et al.,1999), which may be due to shorter freezing time (about 5 h) leading to small values of effective stress in the upward freezing experiment as well as the strengthening effect of cement within rock like sandstone.The consolidation in unfrozen regions was beneficial for reducing scattering attenuation and increasing received wave energy.However, this function may be counteracted or even reversed by some air or possibly microscopic bubbles that replaced unfrozen water in tiny pores of unfrozen regions, when water migrated towards the freezing front and larger pores in the sandstone during early freezing stages,according to acoustic parameter variations.

Fig.13.The values of (a) fc and (b) KFS of sandstone samples during upward and uniform freezing experiments.

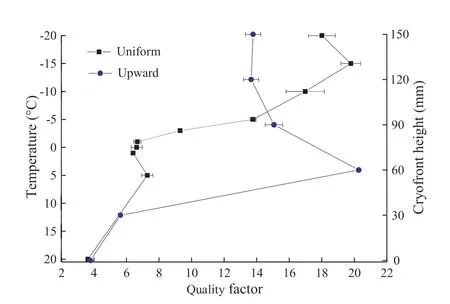
Fig.14.The quality factor Q of sandstone during upward and uniform freezing experiments.Error bars indicate standard deviation of samples 1-5 (blue) and 7-9(black).

4.2.Mechanism of changes in ultrasonic parameters during upward and uniform freezing

Reflection, refraction and transmission of P-waves between unfrozen and frozen regions (Section 2.3.1), separated approximately by the position of the cryofront, can explain why the variations of ultrasonic parameters during upward freezing was quite different from that during uniform freezing.Fedorov (1968) and Rokhlin et al.(1986) indicated that a major problem in understanding wave propagation concerns the reflection and transmission of elastic waves from a rigidly coupled interface between any two media.Degtyar and Rokhlin (1998) found that wave reflection and transmission are most remarkable near critical angles when elastic wave is transmitted through an solid-solid interface.Liu et al.(2007, 2012) investigated the reflection and transmission of acoustic waves, and found that the energy reflection coefficient is affected by uniaxial stress in rocks.Salisbury et al.(2003)proposed a method to calculate the reflection coefficient for a normal-incidence P-wave by comparing the impedance of felsic and mafic rocks.Du et al.(2001) found that the reflection and refraction coefficients between the solid-solid plane is related to wave velocity, density and angle of incidence.Zhang et al.(2020)calculated the reflection and refraction coefficients of an artificially frozen wall boundary (between 0°C and -4°C) based on a normal-incidence P-waves hypothesis.

P-waves in our experiment can be simplified as normalincidence P-waves,thus the reflection coefficient rφand refraction coefficient tφduring upward freezing can be calculated as

where Z1,ρ1, and Vp1are the acoustic impedance (N s/m3), density(kg/m3) and P-wave velocity (m/s), respectively, of the upper unfrozen region (Fig.7b); and Z2, ρ2, and Vp2are the corresponding parameters of the lower frozen region(Fig.7b).The P-wave velocity of sandstone in the direction of stratification(face A to C,and B to D)at different detection heights(around 30 mm,75 mm and 120 mm)was measured in the laboratory during upward freezing (Fig.15).Wave velocity increased after the cryofront arrived at the UT detection heights due to ice crystals filling the pores of sandstone gradually.The calculated changes of Z1,Z2,rφand tφduring upward freezing are shown in Fig.16.

Fig.16 shows that the acoustic impedance increased significantly after the unfrozen region was frozen, whereas it changed slightly in unfrozen or frozen regions.Therefore, the values of rφand tφwhen the cryofront reached heights of 30-90 mm were higher than that at other heights.The more the P-waves reflected or refracted around the cryofront, the more the P-wave attenuation and wave energy reduction induced.The change in head wave amplitude during upward freezing can indicate the reflection and refraction of P-waves (Section 3.2.3).Furthermore, Salisbury et al.(2003) indicated that a value of rφas low as 0.06 can be readily detected by the seismic-reflection method (SRM).By implication,the freezing state of rock during upward freezing (artificial frozenwall development)might be detected by SRM during early stages of freezing, and this merits further study.

The relationship between temperature T and Vpwas quantified by a piecewise function (Eq.(8)), according to the experimental results from uniform freezing (Section 3.2.2).The coefficient of determination (R2) of Vpranges from 0.9979 to 1.

The change of acoustic impedance during upward freezing can be expressed as

Therefore,the acoustic impedance field during upward freezing can be estimated from the temperature field monitored by the temperature sensors.As shown in Fig.17, the acoustic impedance field can be divided into three regions: (1) An upper region(0.4 × 107-0.6 × 107N s/m3) - ‘1’ in Fig.17 - with decreased thickness as the cryofront rose to 150 mm.In this unfrozen region,the value of acoustic impedance was far lower than that in other regions.Thus,most of the refraction was attributed to microcracks,large pores and defects in unfrozen sandstone.The ultrasonic waves propagated along the shortest time path in the uniform temperature field according to Fermat theory (Wei et al., 2020).Therefore, a large temperature difference (-1°C-20°C) in this region led to complex wave path and low wave velocity.(2) A middle region (0.6 × 107-0.85 × 107N s/m3) - ‘2’ in Fig.17 -developed around the rising cryofront.The narrow vertical extent of this region indicated that a steep acoustic impedance gradient existed across a small distance, which is the interface of reflection and refraction.The narrow band was centered around the cryofront before the cryofront arrived at 90 mm,and then it gradually lagged behind the cryofront.The width of the band gradually increased,and almost covered the unfrozen horizon after the cryofront arrived at 120 mm.It is a major reason for multiple frequency components and decreased dominant frequency,and Q-value after 120 mm.(3) An lower region (0.85 ×107-1 ×107N s/m3) - ‘3’ in Fig.17-with increased thickness as the cryofront rose to 150 mm.It is shown that the value of acoustic impedance in the frozen region was far higher than that in other regions.Most microcracks,large pores and defects were probably filled by ice crystals, which reduced refraction significantly.However, a large temperature gradient (-20°C to -1°C) in this region also resulted in complex wave paths.

Fig.15.Vp of sandstone in the direction of stratification (face A to C, and B to D) at different detection heights (around 30 mm, 75 mm and 120 mm) when the cryofront arrives at six heights during upward freezing.

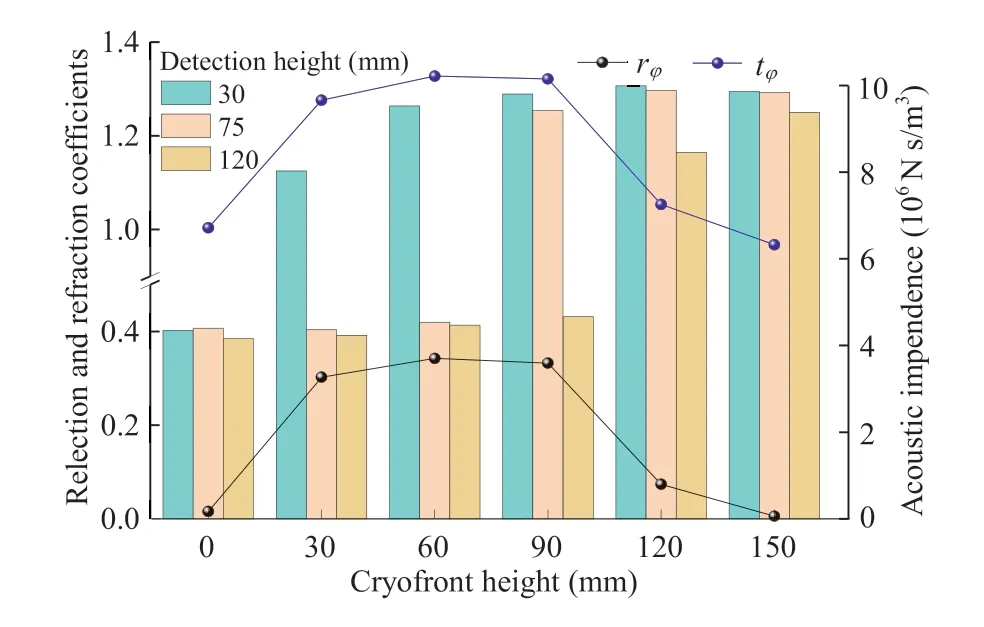
Fig.16.The changes of acoustic impedance and coefficients during upward freezing.

Obviously, the continuous changes of the reflection coefficient rφ, refraction coefficient tφand acoustic impedance field are the major reasons for large reflection and refraction during upward freezing, which lead to irregular ultrasonic time-frequency characteristics except for wave velocity.

The main reason for scattering attenuation and diffraction or refraction propagation during uniform freezing is the changes of porosity,contact area and microcracks in the sandstone(Sams et al.,1997; Wang et al., 2015b).The ice matrix increased the number of connections and stiffened the framework with the temperature below -5°C, favoring lower P-wave attenuation and higher wave energy(Section 3.2.1).Therefore,more acoustic parameters can be used to evaluate the freezing state of rock that is frozen uniformly rather than progressively upward.

4.3.Evaluating the freezing state of frozen sandstone

From the results in Sections 3.2-3.4, the ultrasonic timefrequency characteristics continually changed with both uniform and upward freezing, suggesting that this method can be used effectively to assess the freezing state of sandstone subjected to both thermal protocols.

4.3.1.Evaluating the freezing state during uniform freezing

In terms of uniform freezing, the time-domain indices in the terms of wave velocity Vp, and head wave amplitude Ah, and the frequency-domain indices in the terms of centroid frequency fcand quality factor Q were adopted as ultrasonic parameters for evaluating the temperature(T) of uniformly frozen sandstone.

A radar chart of these four ultrasonic time-frequency parameters is shown in Fig.18.Each parameter value corresponds to a certain temperature according to Sections 3.2-3.4, the results of which are connected to a quadrilateral area.The brown area represents unfrozen sandstone above -1°C, while the mauve area represents frozen sandstone below -10°C.As indicated above,these four ultrasonic parameters can be used as an effective way to assess quantitatively the temperature (T) of frozen sandstone.

The detailed evaluation process is as follows.First, the four ultrasonic parameters were measured or calculated.Second, each measured parameter value was drawn at the corresponding values of the ruler lines.Third, four points were connected to form aquadrilateral measured area.Finally, this area was compared with an colored quadrilateral area in Fig.18.If most of the quadrilateral measured area covers the mauve area, it indicates that the frozen sandstone is below -10°C, because the designed average temperature used in AGF in the field is commonly -10°C.

Fig.17.The changes of acoustic impedance and coefficients during upward freezing.Units of legend are in N s/m3.

Fig.18.A radar chart of ultrasonic time-frequency evaluation based on the temperature for uniform freezing.

4.3.2.Evaluating the freezing state during upward freezing

In terms of upward freezing, as illustrated in Sections 3.2-3.4,the time-domain index Vpcan indicate the cryofront height,whereas the multi-peaked frequency value of frequency spectrum can reveal the frequency of different regions during upward freezing.Few frequency-domain index values can be used to evaluate the freezing state during upward freezing because of complex reflection, refraction and transmission characteristics when ultrasonic waves travel though the samples (Section 4.2).

Vpcontinuously increased as the cryofront rose according to Sections 3.2.2.Therefore,if wave velocity during the later stages of freezing was equal to or lower than that during early stages, this suggests an abnormality and indicates that the artificial frozen wall was influenced by high seepage or other geological factors related to faults, cavities and interbedded strata, which can provide early warning and forecast of artificial frozen wall development.

The cryofront height within upward frozen sandstone can be calculated by a piecewise function according to the experimental results in Sections 3.2.2:

The coefficient of determination(R2)of Eq.(10)is 0.9899,which shows that the regression precision is high and Vpcan be used as an effective way to assess quantitatively the cryofront height (H) of upward frozen sandstone.

A simplified model to calculate frozen section thickness of fine sand during upward freezing was established in our previous study(Zhang et al., 2021a), which can be expressed as

where Sfis the thickness of the frozen section(mm);S is the sample height(mm);and vfand vuare the average wave velocities of frozen and unfrozen sections (km/s), respectively.

The two parameters in Eq.(11), i.e.S and τp, can be measured directly,whereas vuand vfare difficult to determine accurately due to the continuously changing temperature during progressive upward freezing.But the values of vuand vfcan be estimated by measuring the P-wave velocity of sample in the direction parallel to the stratification (face A to C, and B to D in Fig.3) at different detection heights during upward freezing.As shown in Fig.15,the wave velocity of the unfrozen section at 75-120 mm height slightly changed before the cryofront arrived at 60 mm and its values were similar to those of saturated sandstone before upward freezing.Therefore, vucan be regarded as the wave velocity of unfrozen sandstone,a parameter that is directly measurable prior to freezing.Similarly,P-wave velocity of the frozen section at 30-75 mm height changed from 4.548 km/s to 4.632 km/s after the cryofront arrived at 120 mm, which approximated the wave velocity of frozen sandstone at -10°C to -15°C.vfcan be regarded as the wave velocity of frozen sandstone at -10°C, given that the designed average temperature used in AGF in the field is commonly-10°C.

According to the results of our experiment, S is 150 mm, the average values of vuand vfof samples in the direction perpendicular to the stratification are 2.177 km/s and 4.559 km/s,respectively,and τpis detected at different stages of upward freezing.Substituting the above parameters into Eq.(11), the thickness of the frozen section is calculated and illustrated in Table 2.The accuracy of predictions ranged from 73.37%to 99.23%,and it decreased first and then increased as the cryofront rose.The main reason for the changing accuracy is that the proportion of partially frozen rock located near the cryofront(with a wave velocity of 3.717 km/s and 4.379 km/s, respectively, when the cryofront reached 30 mm and 90 mm) is close to that of unfrozen and frozen sections when the cryofront rose from 60 mm to 90 mm.By contrast,the unfrozen and frozen sections accounted for a larger proportion when the cryofront was below 60 mm and above 90 mm, respectively.More scattering attenuation is expected in three sections (unfrozen,partially frozen, and frozen) than in one section (unfrozen or frozen) when ultrasonic waves propagate through rock of similar thickness.Obviously,a simplified model of frozen section thickness can be extended to upward frozen sandstone.

Table 2Calculated and measured values of frozen section thickness.

Unfortunately, single and multiple peaks in the frequency spectrum, however, cannot be used as an effective way to identify the freezing state, though they can be used for fine sand (Zhang et al., 2021a).Two main reasons may account for the different frequency spectrum rules (Draebing, 2016) between fine sand andsandstone:(1)Mineral components that are anisotropic,as well as textural or structural properties(e.g.lamination)in sandstone lead to a multi-peaked frequency spectrum characterizing upward freezing.Such anisotropy may also result in an uneven distribution of water within the rock.By contrast, unfrozen fine sand that has been remolded prior to UT is more isotropic in its physical properties and distribution of water, which probably accounts for its single peak.(2)The higher frequency components of P-waves were more easily absorbed in fine sand than those in sandstone,because only the latter is cemented.It is hypothesized that the three peaks represent air,liquid water and matrix in sandstone before freezing.

More generally, the frequency spectrum could be used as a convenient and rapid method to identify different freezing states of sandstone (unfrozen, upward frozen, and uniformly frozen).A multi-peaked frequency spectrum with a low dominant frequency(2.44-12.21 kHz)is characteristic of unfrozen sandstone,whereas a multi-peaked frequency spectrum with a higher dominant frequency (24.41-34.18 kHz) is characteristic of upward freezing sandstone,and single-peaked frequency spectrum with the highest dominant frequency (38.95-44.33 kHz) is characteristic of uniformly frozen sandstone (below -5°C).

4.4.Implication to frozen ground engineering

The implication of this experimental study to frozen ground engineering is that the method of ultrasonic time-frequency can be applied to AGF engineering projects in sandstone.This method avoids problems related to the small number and fixed location of thermometer holes installed in the field.In application,this method can be used in two stages of AGF: (1) The thickness of frozen wall between the freezing hole and the ultrasonic measuring hole during the active freezing stage can be calculated by Eq.(10)or(11).If wave velocity increases little or slowly, the frozen wall may be influenced by substantial groundwater seepage or other geological factors related to faults, cavities and interbedded strata.(2) The radar chart of ultrasonic time-frequency parameters(wave velocity Vp,head wave amplitude Ah,centroid frequency fcand quality factor Q) could be used to evaluate the average temperature of frozen sandstone between any two freezing holes in the freezing state evaluation stage.If most of the area is obviously smaller than the brown area, it may be caused by inadequate strength of frozen sandstone or by an unfrozen region within a frozen wall between two freezing holes due to substantial groundwater seepage.

5.Conclusions

We draw the following conclusions from our experiments on progressive upward freezing and uniform freezing at a series of falling temperatures maintained at the time of acoustic measurement in a steady-state and spatially uniform condition throughout the blocks:

(1) Received ultrasonic waveform change was broadly similar in both experiments: the period of the received waves increased and coda waves changed from loose to compact.The main difference between the experiments was that upward freezing delayed the appearance of received compact waves due to wave attenuation in unfrozen sections and reflection between unfrozen and frozen regions.

(2) Wave velocity changes during upward freezing were totally different from those associated with the falling temperature series.During the latter,Vpincreased in three stages:(i)little increase at temperatures above -1°C, (ii) substantial increase between -1°C and -5°C, and (iii) slow increase between -5°C and -20°C, whereas Vpincreased more orless uniformly during upward freezing.Wave velocity change of uniformly frozen rock can be directly used to evaluate frozen wall development during AGF, and wave velocity change during progressive upward freezing can reveal cryofront height and determine frozen wall development.

(3) Head wave amplitude changes during both experiments were somewhat similar.During upward freezing,head wave amplitude decreased continually at first,and then increased gradually with rising cryofront position,whereas during the falling temperature series, head wave amplitude decreased as temperature dropped above 0°C and increased continually until temperature dropped to -15°C.Wave amplitude cannot be used as an effective way to evaluate frozen wall development in AGF.

(4) Frequency-spectrum changes during upward freezing were quite different from those associated with the falling temperature series.The frequency spectrum became more regular and single-peaked gradually as temperature decreased until -15°C during the latter, whereas multi-peaked frequency spectrum always characterized upward freezing.However, the frequency components when the cryofront reached 150 mm can show the frequency of different regions of freezing.

(5) The continuous changes in the reflection coefficient rφ,refraction coefficient tφand acoustic impedance field are the major reasons for large reflection and refraction during upward freezing compared with uniform freezing.

(6) Wave velocity Vp, head wave amplitude Ah, the centroid frequency fcand quality factor Q were adopted as ultrasonic parameters to evaluate quantitatively temperature (T) of uniformly frozen sandstone, and their application within a radar chart is recommended.Vpprovides a convenient method to evaluate the freezing state and calculate the cryofront hight and thickness of the frozen section during upward freezing.The accuracy of calculated values of thickness of the frozen section varied between 73.37% and 99.23% in this experiment.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The research was financially supported by the National Natural Science Foundation of China (Grant Nos.51804157, 51774183, and 11702094), and the University of Sussex, UK.Both are gratefully acknowledged.We thank the anonymous referees for their comments on earlier versions of the manuscript,which have improved it substantially.