一道2022年希望联盟夏令营试题的解法探究与推广

汪国平

(安徽省枞阳中学 246700)

2022年中国数学奥林匹克希望联盟夏令营试题(一)第7题为：

已知△ABC为锐角三角形，A,B,C为其三个内角，则2cotA+3cotB+4cotC的最小值为．

这道试题考查解三角形，所给条件简洁，内涵丰富，试题难度适中，考查学生的逻辑推理、数学运算等核心素养．试题的解法较多，关键在于合理的推理转化，下面先从不同角度给出该题的解法探究，最后探讨得到一般性的结论．

1 解法探究

命题组提供的参考答案技巧性太强，不适合临场考试.下面笔者基于学生的视角对解法进行探究，整理成文，与读者探讨．

视角1 立足恒等式cotAcotB+cotBcotC+cotCcotA=1．

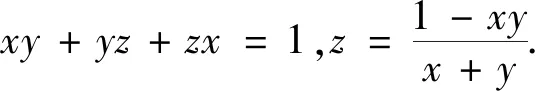
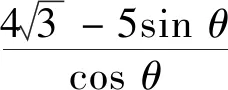
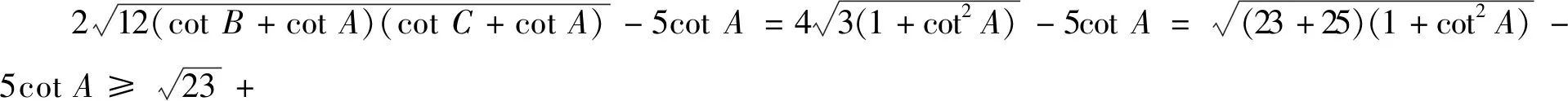
评注上述三种方法本质上没有太大差异，只是最后表现形式不同而已.解法1、解法2在恒等式的基础上进行代数换元、三角换元，构造均值不等式、辅助角公式；解法3在前两种解法的基础上进行了优化，大大简化了计算量．

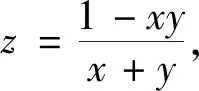
①若△ABC为锐角或直角三角形，显然成立；

②若△ABC为钝角三角形，此时只需证明z<0的情况即可．

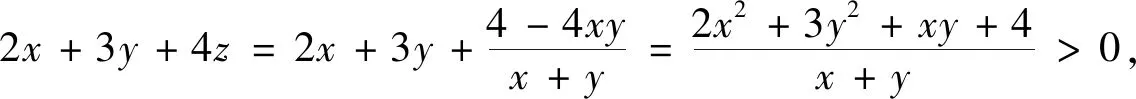
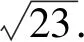
评注上述两种解法构造方程，利用Δ≥0．

视角2 立足于恒等式tanA+tanB+tanC=tanAtanBtanC(*)．

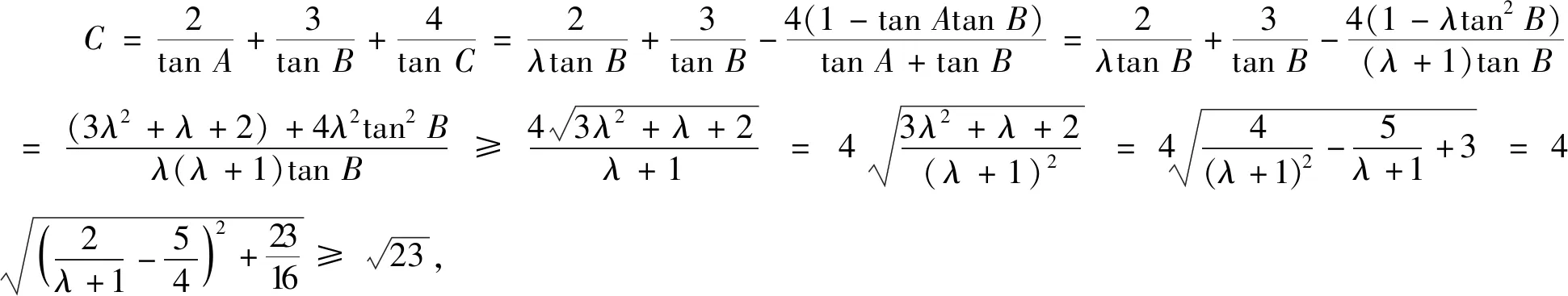
评注解法6是一种倍值换元法，实现消元，转化为函数问题．

视角3 立足基础，实现计算．

评注解法7采用解三角形中最基本的方法：利用正弦定理、余弦定理化简所求表达式，结合辅助角公式求出最小值．

视角4 几何视角(作高)．

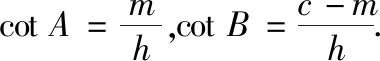
图1

评注解法8化任意三角形为直角三角形，转化为以m为主元的二次函数，结合均值不等式求得最小值．

2 试题推广

一道题是不变的，方法多样，在探究其解法之后，更要尝试对其进行推广．