解析几何中非对称结构问题的多层次转化

黄森霞

(江苏省常熟中学 215516)

解析几何的图形本身具有高度对称的特点，但是在解析几何问题中，往往会出现一些非对称结构，比如在处理定点定值这一类问题时，经常会遇到结构不对称、图形动态轨迹不对称等问题．“非对称”是指图形或物体相对某个点、直线或者平面而言，在内容、大小、形状和排列上具有差异性．如何将不对称问题转化为对称问题，是解决这一类问题的关键．

下面是一道以定值问题为背景的解析几何题，笔者在一次课上尝试从三个不同的层次将其转化为对称问题来处理．

1 问题

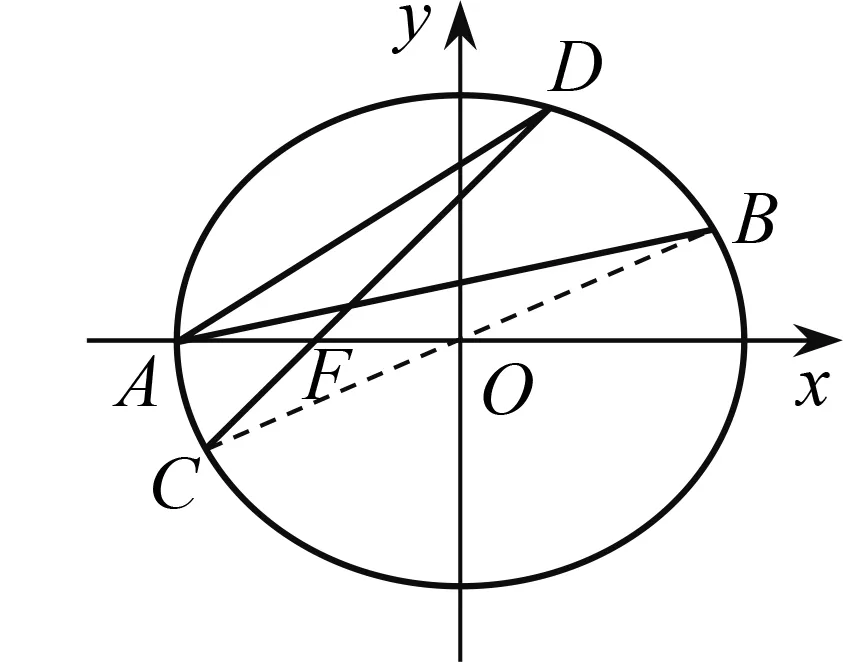
图1

(1)求椭圆E的标准方程；

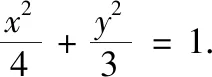
2 层次1——对于韦达定理非对称结构的转化

方法1 和积转化，整体消元

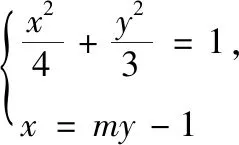
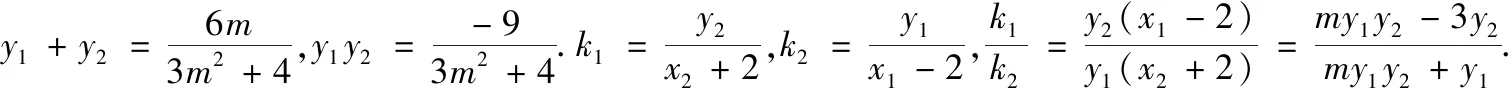
评注在目标式中，出现了两根的非对称结构，不能直接代入韦达定理进行运算，此方法是借助于韦达定理的两根之和与两根之积的等量关系，先将积转化为和，再与单独的根合并后重新整合，以此达到整体消元的目的．其关键式子是λy1y2=μ(y1+y2)．

方法2 部分代换，整体消元

方法3 平方升幂，曲线代换

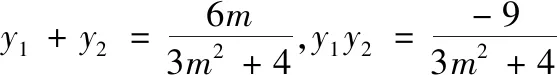
3 层次2——对于目标式非对称结构的转化

方法4 转化目标，韦达定理

图2

即转化为求证k1k3为定值问题．

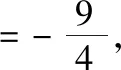
方法5 转化目标，方程同构

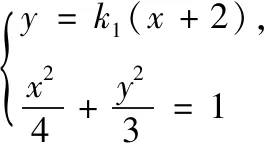
方法6 转化目标，构造齐次

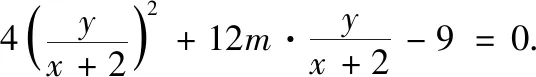
4 层次3——从结构上直接进行齐次转化

方法7 转化目标，结构齐次

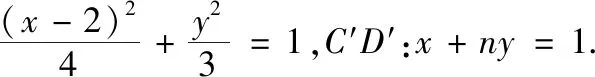
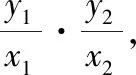
5 回顾与反思

对于本题非对称结构的处理上，三个层次层层递进.

第一层次是针对运算过程中的非对称结构的式子，如何利用韦达定理的对称性或者椭圆方程的对称性进行转化，使之出现对称的可用韦达定理的结构形式．这一层次的思维要求并不高，适合所有联立方程后的韦达定理不可用的转化，其难点是在计算中运算量较大，需要有一定的计算功底．

第二层次是从问题的本质出发，对于目标式不对称的原因进行思考，只要将其转化为一条直线与圆锥曲线相交的两点，那么目标式必然是对称的，而在转化的过程中需利用圆锥曲线图形的对称性.椭圆上关于中心对称的两点与其上任意一点连线的斜率之积为定值，刚好可以转化到目标式的标准对称结构，然后只要正常联立方程，利用韦达定理即可达到目的．这一层次需要抓住圆锥曲线的本质，对其常见结论有一定的了解，才能顺利转化，计算量相对减小．