数学课堂要有“研究”的味道——“裂项相消法求和”教学实录与反思*

郑金宾

(天津市东丽区第一百中学 300300)

1 基本情况

1.1 授课对象

学生来自天津市示范性高中高二学生，具有一定的逻辑思维能力、抽象概括能力和数学运算能力．

1.2 教材分析

“裂项相消法求和”是人教A版选择性必修第二册第四章“数列”的内容，是在学习数列的概念、等差数列、等比数列相关知识之后，围绕数列求和这一特征要素，对数列知识的一次综合和深化．其思想实质是将数列中每项分解，然后重新组合，使之能消去一些项，最终达到求和的目的．这个裂项、相消的过程蕴含着化归与转化、分解与组合、映射与对应、无限到有限、函数与方程思想，有助于发展学生的数学抽象、逻辑推理、数学运算素养，有助于形成理性思维并提升研究能力．

教学目标 (1)了解裂项相消求和法的基本思路，理解其基本原理，形成一般观念；(2)会从数列原型出发，根据数列通项公式的结构特征进行裂项，并能进行适当的拓展、推广；(3)会利用方程的思想判断裂项后是否能够相消，能发现裂项后相消的规律，能应用裂项相消法的思想，创造性地解决一些数列求和问题，做到学以致用．

教学重点 能正确地对裂项相消法的模式进行识别，会用裂项相消法求一些数列的和．

教学难点 数列求和时裂项、相消的发现、归纳过程．

2 教学过程

2.1 单元复习 观念引领

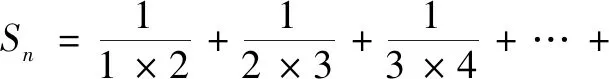
生1：既不属于等差数列求和，也不属于等比数列求和，是一种以前没有遇到的数列求和，解决起来有困难．

师：在数列单元中，数列的前n项和Sn=a1+a2+a3+…+an作为数列的一种重要特征元素，对于描述数列有着极为重要的作用．问题1对我们提出了新的挑战．回忆一下，在以前所学习过的数列求和主题中，我们都接触了哪些方法？

生2：如果数列{an}为等差数列，将Sn=a1+a2+a3+…+an变形为Sn=an+an-1+an-2+…+a1，然后利用a1+an=a2+an-1=a3+an-2=…=an+a1，将两式相加得到Sn，用到了倒序相加法．

生3：如果数列{an}为等比数列，当公比q≠1时，将Sn=a1+a2+a3+…+an变形为qSn=a1q+a2q+a3q+…+anq，然后利用a1q=a2,a2q=a3,…,anq=an+1，将两式相减得到Sn，用到了错位相减法．

师：通过等差数列和等比数列前n项和公式的推导过程，你能从中总结出一些数列求和的思路吗？

生4：可以把数列中的项进行变形，将和的运算进行下去，把无限项求和转化为有限项和的形式．

师：依据数列本身的性质，将数列中的项进行适当变形，通过等量替换、加减消元等方式，将无限项的和转化为有限项和的形式，这就是数列求和的一般观念！

2.2 搭建支架 联想激活

问题2数列a1,a2-a1,a3-a2,…,an-an-1(n≥2)的前n项和Tn如何表示？

生5：因为在数列求和过程中，a2,a3,…,an-1恰好能够正负抵消，所以Tn=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=an(n≥2)，干净利落！

师：受此启发，你能解决问题1吗？

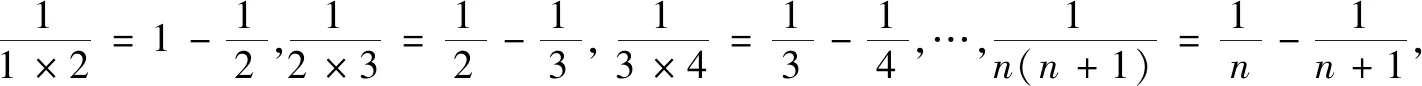
师：漂亮！你是怎么想到的？

2.3 批判质疑 提炼方法

师：生7仿照问题2的解决过程，尝试对问题3中的式子进行了分解，勇气可嘉！对于生7得出的结论，同学们都同意吗？

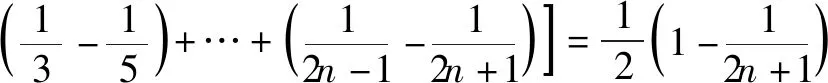
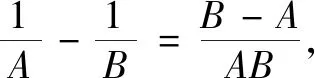
师：这种将数列中的每一项拆成两项的形式，利用正负抵消，将中间的项消去，进而得到其和的方法称为裂项相消法求和，体现了分解与组合、转化与化归、无限到有限的数学思想．裂项是手段，相消是目的．

2.4 分析现象 把握本质

问题4上面两个裂项相消法求和的问题，会与什么类型的数列有关联？

生10：我发现数列{n},{2n-1}是等差数列．

师：有眼光！在题目的背后果然隐藏着等差数列的影子！你能写出这种数列求和的一般形式吗？

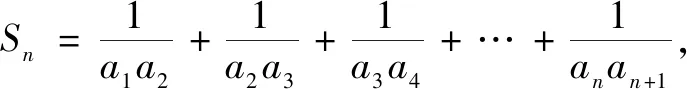
师：看来这种数列求和与等差数列密切相关．如何进行裂项呢？

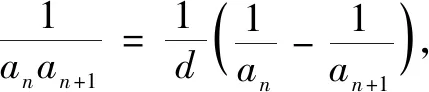
师：谢谢你！我们越来越能看清这种求和形式的本质了．从数列原型——等差数列出发，利用等差数列的性质进行裂项、相消，等差数列的介入为我们解决数列求和问题打开了一扇窗！

2.5 选取原型 改题编题

问题5利用刚才裂项相消法求和的形式，编制一道习题，并试着完成它．

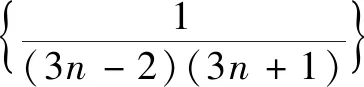
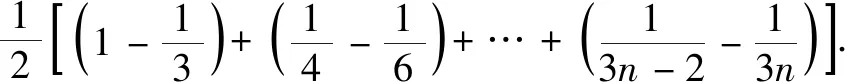
师：为什么不能相消呢？

生12：(沉思片刻)如果令an=3n-2，bn=3n，因为方程an=bm是无解的，所以裂项以后不可能正负相消．

师：非常透彻！构造两个数列，从方程的角度判断方程是否有解，体现了两个数列的项之间的映射与对应关系，揭示了裂项后是否能够相消的根源所在．

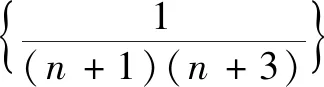
师：请你再阐述一下，裂项后是如何实现相消的？

生13：如果令an=n+1，bn=n+3，因为an+2=bn，所以裂项以后能够实现正负相消，只不过需要隔一项才能抵消，最后正负抵消剩4项．

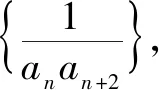
生14：应该可以，只不过正负抵消后会剩2k项．

2.6 联想拓展 抽象推广

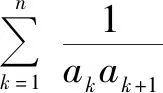
生16：拓展到分母为四项之积……

师：再想一想：能不能把分母拓展为m项之积这种更一般的形式？

2.7 破解定势 形成结构

问题7裂项只有拆成两项之差的形式吗？

师：你能举例说明一下吗？

师：可这样无法实现正负抵消啊！如何变换题目条件使之符合裂项相消的要求？

师：很聪明！引入(-1)n后使得数列的各项符合了裂项相消法的要素，后面的裂项相消也就顺理成章了．

2.8 应用方法 迁移创造

问题8裂项相消法的思想，还能应用到哪些数列求和？

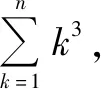
师：非常棒！祝贺同学们得到这么多惊人的发现！“不识庐山真面目，只缘身在此山中”，只要我们能抓住数列问题的规律和本质特征，问题就会迎刃而解，就能揭开数学那层薄薄的神秘面纱！

2.9 总结归纳 提升认识

(1)基本思路：先分解，再组合；(2)基本思想：化归与转化、分解与组合、映射与对应、无限到有限、函数与方程；(3)基本套路：裂项是前提，相消是关键．

3 教学反思

教育从研究中开始，在研究中结束，研究活动要贯穿学生学习活动的始终．在数学课堂上，要淡化对解题技巧的训练，避免把教学的重点放在题型的归纳、解题技巧的掌握上，要消除机械学习、浅层学习弊端，要引导学生以研究者的眼光研究数学问题，分析数学现象，挖掘数学本质，让数学课堂充满研究的味道，从而发挥数学学科的育人价值，提升学生的数学学科核心素养，促使深度学习发生．

3.1 观数学：培养研究意识，加强对数学一般观念的引导

数学课堂上要基于问题解决的需要，让学生经历以“一般观念”为引导，发现规律、获得猜想，并通过推理论证证明结论的过程，培养学生的研究意识，提高学生“观数学”的能力．围绕“数列求和”这一核心概念，要加强对“如何思考”“如何发现”“如何解决”的启发和引导，如数列求和是如何实现从无限项和到有限项和的转化的？裂项是如何实现的？相消是如何实现的？应用裂项相消法能解决具有什么特征的数列求和？在这些“一般观念”的引导下，促使学生主动探究、深入研究．

3.2 联数学：勾联研究内容，加强数学知识间的关联

数学课堂上要基于学生的已有学习经验，充分调动学生联想、想象、猜想意识，让学生经历从单元的视角建立知识间有效关联的过程，培养学生“联数学”的能力．围绕“裂项相消法”这一核心知识，建立所研究数学问题的承重墙，打通不同数学内容的隔离墙，将相关内容从幕后推向前台，实现数学知识的深度勾联，提高学生“联数学”的能力．从数列原型出发，建立所求数列与数列原型的联系，有利于发现数列通项公式的结构属性；从分式的加减法运算出发，建立数列通项公式与分式运算的联系，有助于裂项相消过程的探求，使得裂项相消的探究成为与已有学习经验相互融合的过程．

3.3 变数学：变换研究形式，突出对数学本质的认识

数学课堂上要基于所研究数学问题的本质，对数学问题进行典型的变式，让学生经历在变式中寻求不变性，从而深刻揭示数学问题本质的过程，培养学生“变数学”的能力．围绕裂项相消中“分解与组合”这一本质属性，给予分解与组合丰富的变式样态与表征形式.如将数列的通项公式变式为两项之差(和)的形式；将分母的两项之积变式为三项、四项……m项之积；让学生在数列通项公式的变化中深刻领会如何去裂项、如何进行相消，探究最大限度的一般化模式，在更大范围内进行概括与归纳，形成系统性、普适性的思维结构．

3.4 辨数学：改变研究角度，体现对数学知识的批判

3.5 用数学：应用研究成果，体现对数学知识的再创造

数学课堂上要基于所研究数学问题的价值与意义，让学生经历将获取的数学知识、数学结论、数学方法应用到新的真实情境中，在再创造的过程中培养学生“用数学”的能力．“裂项相消法”不仅仅给学生提供了一种解题方法，更重要的是给学生提供了一种思维方式，即如果能把数列中的每一项分解，再重新组合时能够消去一些项，那么就可以得到数列之和．教师要鼓励学生大胆地应用这样的思维方式，去创造性地构造数列求和，让学生发现一些以前从未发现的方法，解决一些以前未能解决的数学问题，如3+5+7+…+(2n+1)，12+22+32+…+n2，13+23+33+…+n3……发散思维，另辟蹊径，体验成功，将应用研究成果的过程变为学生再创造知识的过程，将学数学的过程变为“玩数学”的过程，其乐融融，其乐无穷！