双线圈式磁流变阻尼器优化设计及减振特性试验研究
马 梁, 范 杰, 李诚昊, 韩祉炫, 王 俊
(1.中国民航大学 天津市民用航空器适航与维修重点实验室,天津 300300;2.清华大学 摩擦学国家重点实验室,北京 100084; 3.西北工业大学 航空学院,西安 710072)
旋转机械常常受到转子振动问题的困扰,严重时将造成其寿命缩短[1]。目前常在支撑区域设置挤压油膜阻尼器来降低转子振动响应[2-6],但作为一种被动控制方式具有减振特性单一的问题。所以发展具有多样减振特性的减振方式十分必要。
磁流变阻尼器是一种可以产生连续可控阻尼的减振装置,既能达到被动控制的效果,也能克服被动控制减振特性单一的问题[7],展现出良好的应用前景[8-13]。近些年,国内外学者和科研人员对磁流变阻尼器的设计、优化和应用进行了大量研究,设计出许多不同结构、功能各异的磁流变阻尼器。其中,较为常见的是活塞式磁流变阻尼器[14-17],此类结构大多基于剪切模式。线圈通常缠绕在活塞上,通过活塞运动使得腔内的磁流变液在压差作用下通过间隙,此时线圈产生的磁场作用于间隙处的磁流变液,进而产生轴向剪切阻尼效果。此外,还有旋转式磁流变阻尼器结构[18-20]。该阻尼器大多也基于剪切模式,但剪切方向与活塞式不同。磁流变液置于转子和定子之间,转子部件转动会对磁流变液产生周向剪切作用,此时磁流变液流动状态改变会对转子形成旋转阻尼作用。而在轴类部件上较常使用的是支撑轴式磁流变阻尼器结构[21-26],这种结构大多基于挤压工作模式。转子径向振动对磁流变液形成挤压作用,油膜处所产生磁场可改变磁流变液流动状态并产生径向阻尼效果。除上述提到的三种典型结构外,根据磁流变阻尼器的应用场合以及所需功能不同还有其他各式各样的结构类型[27-28]。各类磁流变阻尼器多采用磁回路闭合设计方法,以满足磁场在指定工作区域的磁感作用。然而,影响磁流变液工作状态的参数不仅只有磁感强度,还应考虑如磁场分布均匀度、磁回路响应速率等因素,都对阻尼效果有较大影响。同时,在磁流变阻尼器参数设计过程中,磁场性能与结构特性难以兼顾,往往无法达到主、被动减振效果的有效耦合叠加,使阻尼器的振动控制工作范围大大降低。
基于上述问题,本文将磁流变阻尼器应用于转子系统,在设计形成闭合磁回路基础上,综合考虑磁场性质、磁路性质、阻尼器结构特征以及三者之间的相互作用关系和对磁回路的反馈作用,设计出一种基于挤压工作模式的双线圈磁流变阻尼器,同时总结得出一套磁流变阻尼器的设计方法。针对双线圈磁流变阻尼器的关键结构参数进行了多目标优化设计,并通过磁场测试验证了所设计阻尼器结构的合理性。然后,将优化后的磁流变阻尼器引入到转子系统中,搭建了磁流变阻尼器支承下转子实验台,通过试验获得了磁流变阻尼器支承下转子系统振动响应的主要时域特征、频域特征以及轴心轨迹特征等,研究了磁流变阻尼器对转子系统振动特性的影响。
1 磁流变阻尼器总体设计
总体设计目标是在满足磁感强度足够且磁场分布均匀的基础上,同时保证磁回路整体漏磁较少且响应速度较快。对整体磁路进行规划,考虑阻尼器部件的相互耦合特性,进行各参数优化选择,完成阻尼器总体设计目标,具体流程如图1所示。

图1 磁流变阻尼器总体设计流程Fig.1 Overall design flow chart of MR damper
1.1 磁路设计与计算
首先对磁流变阻尼器进行整体磁路设计。磁路设计的目的在于使励磁线圈产生的磁通在闭合磁回路中以最小的漏磁损失到达油膜工作面处。磁路主要在壳体和鼠笼等支承构件中形成,要避免磁路中元件(壳体、鼠笼)先于油膜工作面处的磁流变液达到饱和。
1.1.1 阻尼器整体结构设计
阻尼器主要由壳体、鼠笼、励磁线圈、隔磁环等组成。励磁线圈产生的磁通穿行于壳体和鼠笼中,线圈下方设置隔磁环,迫使壳体与鼠笼中的磁通引导汇聚在油膜工作面处,形成鼠笼—壳体—鼠笼的闭合磁回路,以达到总体磁回路设计目的。在结构方面,壳体承担了包容线圈、传递阻尼力的作用,鼠笼是改变阻尼器刚度的重要部件,隔磁环为线圈提供了封闭腔室,阻尼器总体满足结构设计需求。具体磁路、结构原理如图2所示。阻尼器结构参数值的大小既会改变各部件结构强度还会影响总体磁性质。如壳体厚度a增大,壳体强度随之增大但壳体内磁路性质和油膜处磁场性质则会随之下降。综合考虑磁性质和结构需求选定初始结构参数如表1所示。

图2 磁流变阻尼器磁路、结构原理Fig.2 Magnetic circuit, structure principle of MR damper

表1 磁流变阻尼器初始结构参数Tab.1 Initial structural parameters of MR damper
阻尼器结构设计应尽量缩短磁力线在磁路中的路径以减小磁阻。壳体应满足以下要求:
(1) 作为重要的磁通引导结构,应选用磁导率高的材料;
(2) 为实现对磁场的实时控制,壳体材料应具有较好的退磁性;
(3) 为保证励磁线圈产生的热量不影响磁流变液的正常工作,壳体材料应具有较好的散热性;
(4) 为使油膜工作面处的磁感强度达到最大,要避免壳体内磁场先饱和;
(5) 为提高能量利用率,应尽量降低壳体内的漏磁。
综上所述,选用磁导率为4 000的电工纯铁作为壳体的材料。隔磁环材料选用金属铝。
1.1.2 励磁线圈安匝数计算
励磁线圈是磁场产生的源头,其安匝数的大小变化是实现磁流变阻尼器半主动控制的主要途径。本文所选用磁流变液(MRF2035)饱和磁感强度为1.0 Tesla,故油膜工作面处的设计磁感强度值应接近或大于1.0 Tesla。油膜工作面处磁通量为
Φ=B×S
(1)
式中:Φ是油膜工作面处磁通量;B是油膜工作面处磁感强度;S是油膜工作面平均半径处面积。
依据等效原则可将整个磁路等效为磁阻结构[29],如图3所示。

图3 磁路及等效磁阻结构Fig.3 Magnetic circuit and equivalent reluctance structure
磁流变阻尼器总磁阻为
Rtotal=R1+R2+R3+RMRF2+
(2)
式中,R1~R8,RMRF1,RMRF2,RMRF3具体形式见附录A。
则磁路的磁通势大小为
F=Rtotal×φ=N×I
(3)
式中:Rtotal为磁路总磁阻;N为励磁线圈总匝数;I为励磁线圈内通入的激励电流。
通过计算,设计总安匝数为4 800。设计通入励磁线圈的最大电流为4 A。因此,两个励磁线圈匝数均为600。
1.1.3 励磁线圈电感计算
励磁线圈的安装形式和数量是影响磁路响应速度的重要参数。由于阻尼器内励磁线圈的空间位置限制,本文采用两支相同参数的励磁线圈作为双磁场源。电磁电路的时间响应为
(4)
式中:τ是时间响应;L(H)是电感;R(Ω)是电阻。在励磁线圈绕线总长度确定的情况下,降低电感L可减小时间响应[30]。因此,本文通过电感表征励磁线圈的响应速度。
励磁线圈自感为L,互感为M,则双励磁线圈电感模型为
L=L1+L2-2M12
(5)
式中:L1是第一励磁线圈电感;L2是第二励磁线圈电感;M12是两励磁线圈之间互感,由于两励磁线圈通入电流方向相反,因此M12取负。
1.2 鼠笼结构设计
鼠笼支承既是实现转子减振的重要构件,也是形成完整磁回路不可或缺的元件。因此,鼠笼的设计必须既满足刚度要求,又满足作为磁路穿行元件的要求。在转轴和转盘参数一定的条件下,通过改变鼠笼结构参数进行其刚度调整,可实现转子系统整体模态的调整,从而避免与工作转速区间相重合。本文所设计的鼠笼弹性支承结构简图如图4所示。
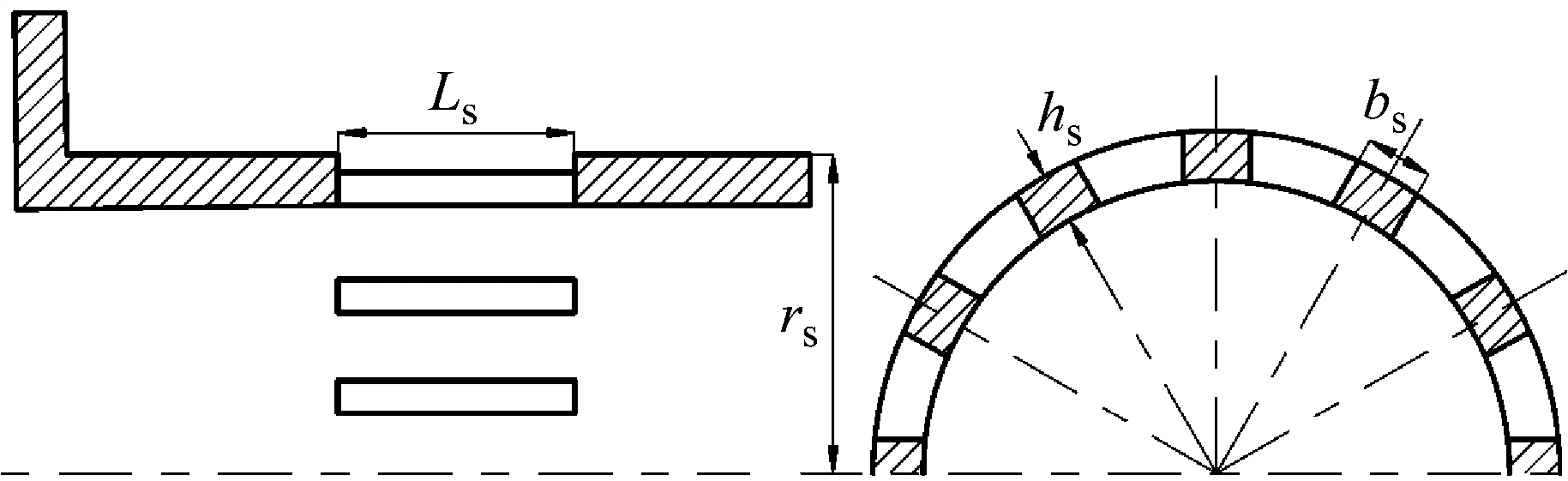
图4 鼠笼模型简图Fig.4 Squirrel cage model sketch
通过分析鼠笼条数目、鼠笼条长度、鼠笼截面积等参数得出刚度近似计算公式如下[31]
(6)
式中:n为鼠笼条数目;E为鼠笼材料弹性模量;hs为鼠笼条截面厚度;bs鼠笼条截面宽度;Ls为鼠笼条长度。
作为形成磁回路的重要元件,鼠笼的饱和磁感强度应大于油膜工作面处磁流变液的饱和磁感强度。鼠笼厚度、长度等是影响磁回路的主要参数,若尺寸太小则鼠笼容易磁饱和。因此基于式(6)并综合调整得到鼠笼结构参数,如表2所示。

表2 鼠笼结构参数Tab.2 Squirrel cage structure parameters
2 磁流变阻尼器多目标优化设计
设计得到的双线圈磁流变阻尼器可基本符合设计目标,但为了最大程度发挥其磁路性能,需对磁路中影响磁感强度的各参数进行优化。在鼠笼—壳体—鼠笼的闭合磁路中,壳体是影响磁路性能的主要元件,而鼠笼的尺寸参数不仅影响阻尼器的刚度还直接决定其磁感强度是否会先于磁流变液饱和。因此,需将壳体和鼠笼作为整体进行结构优化,实现双线圈磁流变阻尼器的磁性质、减振效果和控制效率最佳。
2.1 确定待优化参数及目标
双线圈磁流变阻尼器结构中对磁场产生影响的变量参数有:壳体厚度a、隔磁环轴向长度b、两励磁线圈间连接体厚度c、鼠笼厚度d、隔磁环位置e和两励磁线圈间距离f。为使油膜工作面充分发挥减振作用,设计油膜工作面沿转子轴向总长为36 mm,轴承位于油膜正中央。隔磁环的作用是迫使壳体中的磁力线与鼠笼中的磁力线交汇经过油膜,设计隔磁环轴向长度为8 mm,使其达到迫使磁力线绕行目的。线圈壳体间连接体厚度大小变化对磁场影响较小,其尺寸定为15 mm。为保证油膜工作面处磁场均匀且强度足够,设计两励磁线圈相对位置固定。
经上述调整,最终确定待优化变量参数为:壳体厚度a、鼠笼厚度d和隔磁环位置e共3个变量。待优化参数初始值及参数变化范围如表3所示。

表3 优化变量初始值及变化范围Tab.3 Initial value and variation range of optimization variables

(7)
min{P}
(8)
根据上述待优化结构参数变量及其变化范围,优化目标,采用如图5所示流程进行优化,直至得到最优结构参数。

图5 优化流程Fig.5 Optimize process
2.2 运用最优拉丁超立方生成试验点
最优拉丁超立方设计相对于随机拉丁超立方设计的均匀性更好,生成的试验点均匀的分布在设计空间内,能达到较好的空间均匀填充。运用最优拉丁超立方生成试验参数共40组,其中部分数据如表4所示。
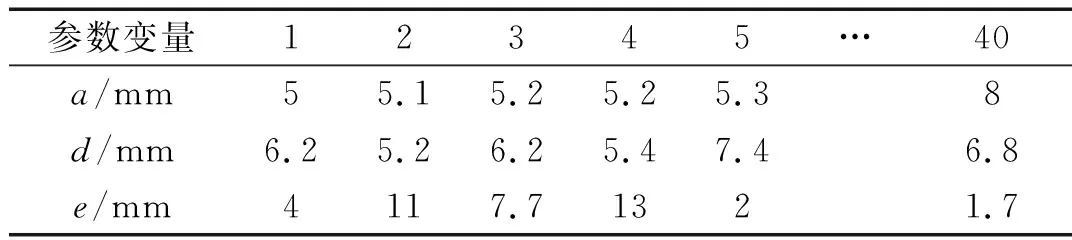
表4 最优拉丁超立方生成部分试验参数Tab.4 The test parameters of the optimal Latin hypercube
2.3 优化结果与分析
对各试验结构参数进行有限元求解,获得计算结果后采用自适应模拟退火算法(ASA)进行参数优化。将优化模型依照ASA算法进行迭代计算,待三个目标函数趋于稳定时,此时部分具有代表性优化结果如表5所示。
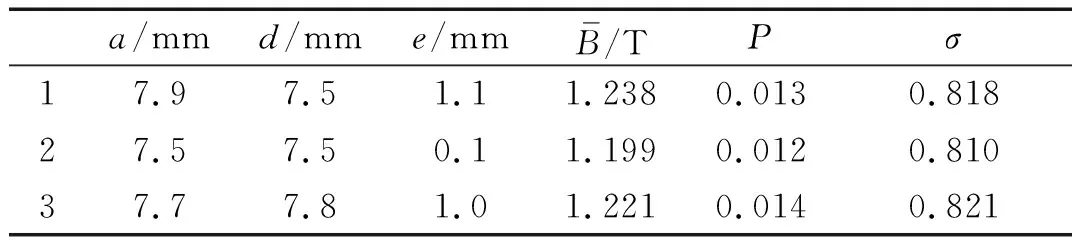
表5 优化后结构参数及目标值Tab.5 Optimized structure parameters and target values
进一步得到不同电流下各结构参数的油膜工作面处平均磁感强度曲线如图6所示。随着通入电流的增加,油膜工作面处磁感强度逐渐增大,在通入电流为3 A时三种模型均达到设计目标,但考虑到模型误差等因素,设计通入最大电流仍是4 A。由图可知,在通入不同电流情况下,结构1在每种状况下的油膜工作面处磁感强度均高于其他结构。

图6 三种结构在不同电流下油膜处的磁感应强度Fig.6 Magnetic induction intensity curve of MRF film working face with different structure under different current
综合考虑最终选取结构1参数作为双线圈磁流变阻尼器最终结构参数。结构1的磁密分布及油膜工作面处磁感强度云图如图7所示。由图可知,油膜工作面处磁场强度足够且分布均匀,满足设计要求。
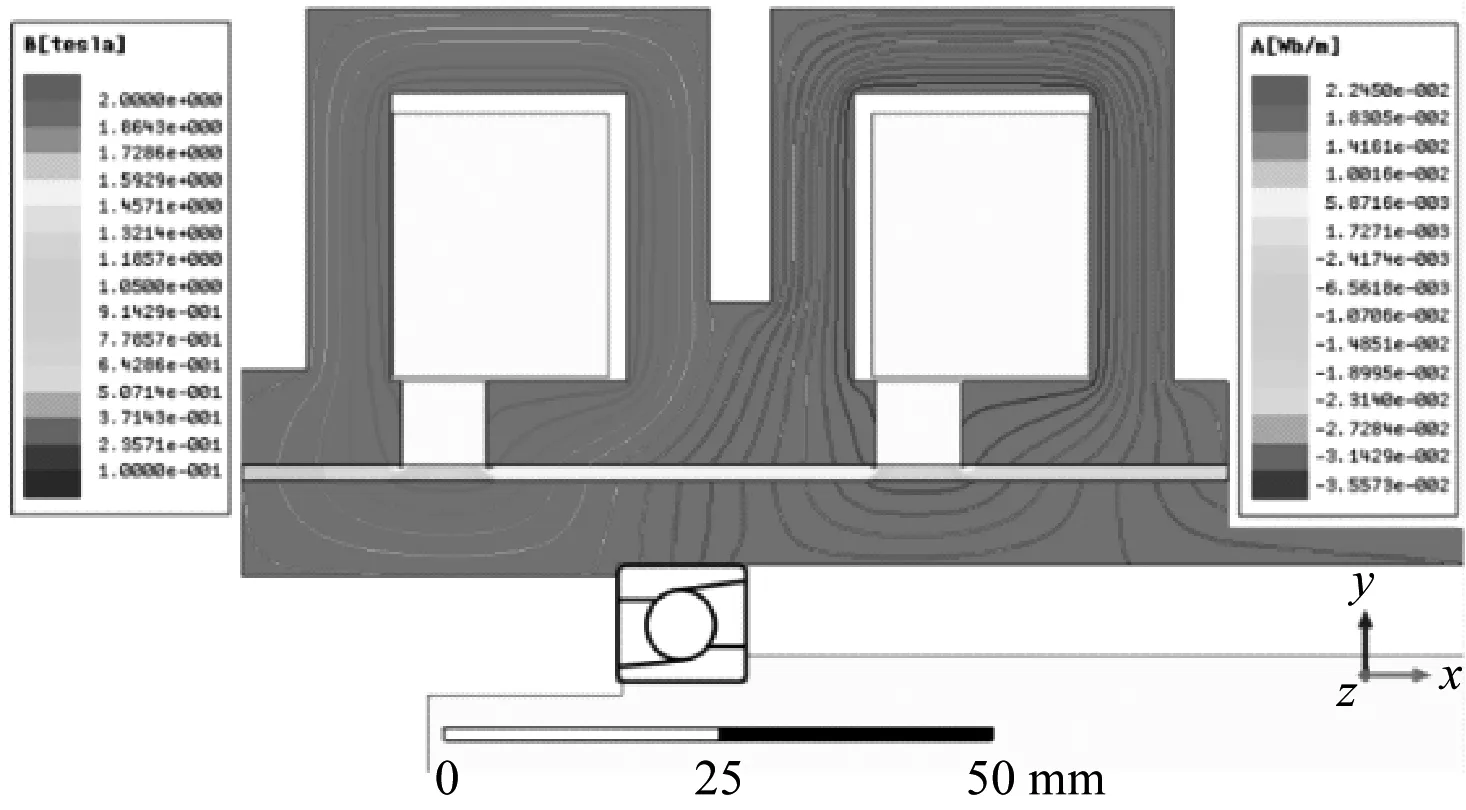
图7 结构1磁路中磁密分布及油膜工作面处磁感强度云图Fig.7 Magnetic flux distribution of magnetic circuit and cloud chart of magnetic induction intensity at MRF film working face
对优化后的结构与原结构进行比较如图8所示,优化后的磁流变阻尼器油膜工作面处磁感强度较优化前提高了20.66%,轴承支撑区域处优化后磁场更均匀,漏磁系数近乎不变,优化效果明显。

图8 优化前后结果比较Fig.8 Comparison of results before and after optimization
3 阻尼器磁场测量试验验证
3.1 磁场测量试验装置
依据最优结构参数,试制了相应的壳体、鼠笼、线圈和隔磁环等部件,如图9所示。

图9 磁流变阻尼器实物图Fig.9 Physical drawing of MR damper
双线圈磁流变阻尼器在油膜工作面处的磁感强度能否达到设计值,需要对目标区域磁场测量后得出结论。本文设计了如图10所示的磁流变阻尼器多维度磁场测量实验台对油膜工作面处的磁感强度进行测量。

图10 磁流变阻尼器多维度磁场测量实验台Fig.10 Multi dimensional magnetic field measurement experimental platform of magnetorheological damper
磁流变阻尼器多维度磁场测量实验台主要由三部分组成:实验台主体、磁流变阻尼器和测量系统。实验台主体的各支撑板所选用的材料均为金属铝,以消除实验台对测量磁场的影响。磁场测量主要依靠霍尔探头伸入到阻尼器油膜工作面中,当所测量磁场垂直于霍尔探头时,传感器将采集相应的磁场信号。
测量试验前首先调整好霍尔探头的径向位置,以避免触碰阻尼器壳体影响测量精度。线圈接通直流电源后,在指定相位探孔中每隔5 mm轴向推动滑块,待读数稳定后记录相应位置的磁感强度值,重复测量三次并取平均值作为该相位的测量结果。沿阻尼器周向每隔90度共四个相位探孔分别进行测量,并绘制油膜工作面处磁感强度变化曲线图。
3.2 试验值与仿真值比较
考虑到霍尔探头在浸入磁流变液中测量时油污会导致测量结果产生较大偏差,所以测量试验在磁流变阻尼器不供油的情形下进行,与试验值对比的仿真计算也相应地将油膜工作面处材料调整为空气。在油膜工作面处设计磁感强度为1 Tesla的环境下,空气的导磁能力弱于磁流变液,因此空气膜的仿真值低于油膜,所以空气膜下的实测目标磁感强度应调整为0.9 Tesla。分别向线圈中通入2 A, 3 A和4 A的直流电,测得四个相位油膜工作面处的磁感强度并与仿真值比较如图11~图13所示。
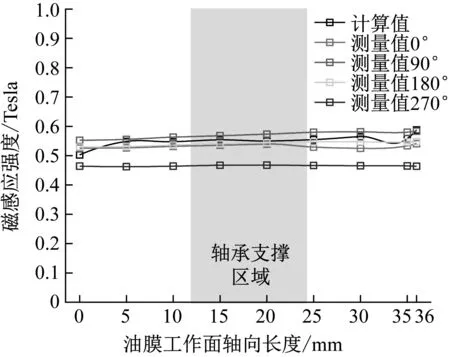
图11 通入2 A直流电时油膜工作面处四个相位测量值Fig.11 Measured value of magnetic induction intensity at oil film working face when 2 A DC is applied

图12 通入3 A直流电时油膜工作面处四个相位测量值Fig.12 Measured value of magnetic induction intensity at oil film working face when 3 A DC is applied

图13 通入4 A直流电时油膜工作面处四个相位测量值Fig.13 Measured value of magnetic induction intensity at oil film working face when 4 A DC is applied
由图11~13可知,四个相位的测量值和仿真值同样具有良好的均匀性,说明双线圈磁流变阻尼器的实际磁路与设计磁路基本吻合。
对四个相位的测量值取平均可得通入电流为2 A、3 A和4 A时所测得的磁感强度均值分别为0.526、0.664和0.782 Tesla。三种电流下的测量结果均表明,0°相位和180°相位测量结果与均值吻合性较好,而90°相位测量结果相对偏大,270°相位测量结果相对偏小。造成上述现象的原因是实验台装配存在同轴度误差(轴心距约为0.05 mm),从而导致油膜厚度较小处(90°相位)测得磁感强度偏高,厚度较大处(270°相位)测得磁感强度偏低。可见油膜处磁感强度对油膜厚度变化十分敏感,且在三种电流下厚度变化总是使得测量结果在偏离均值约10%的范围内波动,此次试验中选择的有效试验值应以0°和180°作为主要依据。
此外,随着通入电流的增加,测量均值与仿真值之间由相差4%增加到15%。因为通入电流增大,阻尼器部件会逐渐趋于磁饱和且漏磁量增加,造成大电流时测量值与仿真值相差较大。
通入电流为4 A且工作面处为空气膜时,实测磁感强度均值为0.782 Tesla,所以在通入磁流变液(MRF2035)时其屈服强度至少可以达到最大值的94%(如图14所示),此时磁流变液已经接近饱和。因此,通入4 A电流足以对磁流变阻尼器形成有效控制。

图14 磁流变液屈服强度随磁感应强度变化曲线Fig.14 Curve of yield strength of MRF with magnetic induction strength
4 磁流变阻尼器支承下转子振动特性试验
4.1 磁流变阻尼器支承下转子实验台设计
将优化后的双线圈磁流变阻尼器引入到转子系统支承中,搭建磁流变阻尼器支承下转子实验台。图15所示为磁流变阻尼器转子试验系统结构。该转子系统采用单盘对称结构,转轴两端通过滚动轴承支承在带鼠笼的磁流变阻尼器上,磁流变阻尼与支座通过螺栓固连。伺服电机通过联轴器与转轴相连,直接为主轴系统提供所需要的工作转速。磁流变阻尼器转子试验系统的实物见图15。

图15 磁流变阻尼器支承下转子实验台设计方案Fig.15 Design scheme of rotor test bench supported by MR damper
4.2 磁流变阻尼器支承下转子系统试验方案
完成实验台装配、对中和动平衡后,进行磁流变阻尼器支承下转子系统不平衡响应试验。本试验通过采集转子振动的位移信号来分析转子系统的振动特性及磁流变阻尼器的减振特性。在实验台接近圆盘端分别沿水平和垂直方向布置两个电涡流位移传感器(如图16所示),并采用支架支承,可以精确调节传感器方向。

图16 实验台测试系统及传感器布置Fig.16 Test system and sensor layout
试验测试所使用位移传感器为江苏联能公司生产的CWY-DO-502型电涡流位移传感器,有效量程为2.00 mm,安装间隙为0.10~0.50 mm,灵敏度为1 μm,采用标准量块进行标定;实验台数据采集设备为德国西门子公司生产的的多通道LMS SCADAS Mobile数采仪,其拥有32个数据采集通道,每通道采样率可达102.4 kHz,满足试验测量需求。数采仪通过以太网方式连接到计算机,通过其配套的数据采集及分析软件进行数据采集、实时显示、选定存储及后期分析等工作,测试现场及设备如图17所示。

图17 转子实验台测试现场Fig.17 Rotor test bench test site
4.3 试验结果分析
本节基于阻尼器静态磁场验证研究结果,考虑转子系统极端工况运行下的最大振幅,将试验最大电流设置为0.4 A,并分别从转速瞬态、电流稳态和转速稳态、电流稳态两个方面研究磁流变阻尼器对转子系统的减振特性,具体如下:
(1) 转速瞬态、电流稳态试验:转子转速从0升速到7 500 r/min,阻尼器分别施加0 A、0.1 A、0.2 A和0.4 A 的稳态电流。
(2) 转速稳态、电流稳态试验:转子以恒定转速运转,阻尼器分别施加0 A、0.1 A、0.2A和0.4 A的稳态电流。
4.3.1 不同电流作用下转子系统幅频响应特性试验
图18所示为转子升速并施加不同控制电流时,转子系统动力学响应的幅频特性图。由图可知,当电流I=0时,随着转速的升高,转子系统的振动幅值逐渐增大,并在转速n=4 700 r/min附近达到最大值。随后,随着转速的增大,振动幅值逐渐降低,因此,4 700 r/min为转子系统的一阶临界转速。随着磁流变阻尼器施加电流的增强,磁流变阻尼器阻尼效应逐渐增强,转子系统在临界转速处的振动幅值逐渐减小。此外可以发现,转子系统的共振转速随着电流的增大而逐渐增大,说明阻尼器的刚度效应也同时在增强。当电流I=0.1 A时,与电流I=0时相比,共振幅值由0.37 mm降低到0.28 mm,降幅约24.3%,同时共振转速由 4 700 r/min提高到4 900 r/min。当电流增大到0.2 A时,转子系统共振幅值进一步降低,由电流I=0.1 A时的0.28 mm降低到0.23 mm,降幅约17.9%,同时共振转速明显提高,由4 900 r/min提高到5 700 r/min。当电流进一步增大到I=0.4 A时,与电流I=0.2 A时相比,共振幅值反而增大,由0.23 mm增大到0.29 mm,说明此时磁流变阻尼器刚度起主要作用,其限制了油膜的挤压作用,进而削弱了磁流变阻尼器的阻尼效果。同时,共振转速进一步提高,由I=0.2 A时的5 700 r/min提高到6 000 r/min。
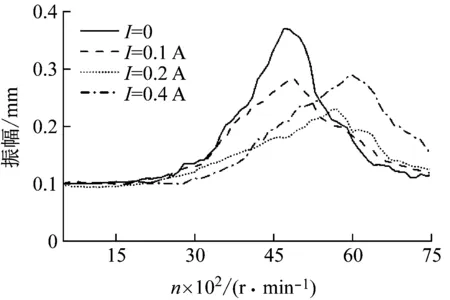
图18 不同电流作用下,转子系统幅频响应Fig.18 The amplitude-frequency response of rotor system under different currents
4.3.2 不同电流作用下转子系统稳态响应试验
图19和图20所示为转速n=3 600 r/min时,不同电流作用下(0、0.1 A、0.2 A及0.4 A)转子系统动力学响应的时间历程图和轴心轨迹图。由图可知,当电流I=0时,时间历程图表现为周期性变化,轴心轨迹表现为一椭圆,转子系统主要受不平衡力影响作同频周期振动。当磁流变阻尼器施加电流I=0.1 A时,磁流变液屈服应力增大,阻尼力增强,与I=0时相比,时间历程图仍表现为周期性变化,但振动幅值减小,且轴心轨迹明显缩小。随着磁流变阻尼器施加电流强度的进一步增大,当I=0.2 A和I=0.4 A时,时间历程图中转子系统的振动幅值逐渐减小,轴心轨迹逐渐缩小。该现象说明磁流变阻尼器能够为转子系统提供有效的阻尼,减小转子系统的振动,且电流越大,阻尼器效果越明显。
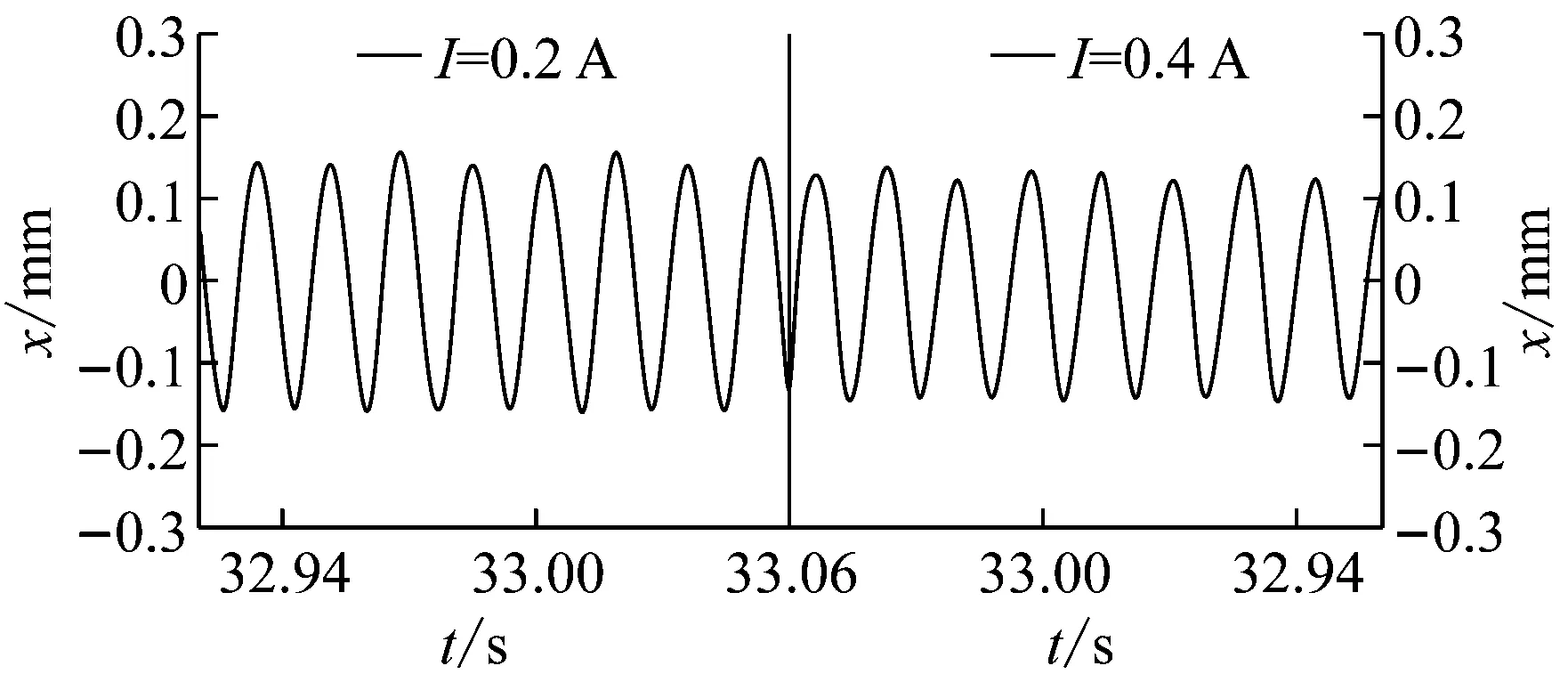
图19 不同电流下,转子系统动力学响应的时间历程Fig.19 The time history of the dynamic response of the rotor system under different currents

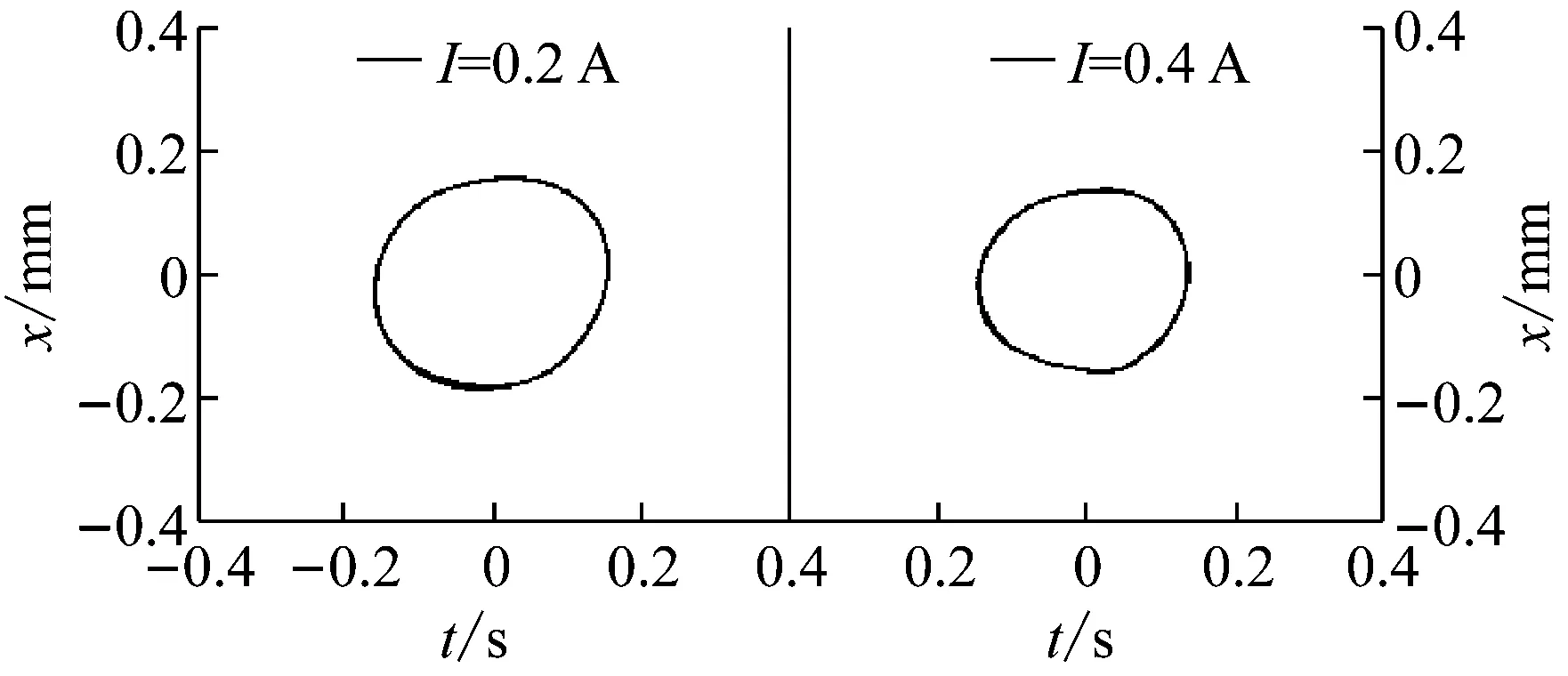
图20 不同电流下,转子系统动力学响应的轴心轨迹Fig.20 The axis orbit of the dynamic response of the rotor system under different currents
5 结 论
本文设计了一种基于挤压模式的双线圈磁流变阻尼器,并对阻尼器结构进行了优化,形成了一套完整的磁流变阻尼器的设计思路。之后对双线圈磁流变阻尼器的油膜工作面磁场进行了测量试验验证。最后,将优化后的双线圈磁流变阻尼器引入到转子系统中,搭建了磁流变阻尼器支承下转子实验台,进行转子系统不平衡响应试验。得到如下结论:
(1) 以阻尼器油膜工作面处的局部磁场特性和整体磁路效率最优为目标,综合考虑磁场性质、磁路性质、阻尼器刚度以及三者之间的相互作用关系和对磁回路的反馈作用,形成了闭环设计方法。
(2) 磁流变阻尼器采用双线圈布置,在阻尼器内部形成了双闭合磁回路,缩短了每条磁回路在磁路中的穿行距离,使得油膜工作面处的磁感强度满足1.0 Tesla的设计要求,较相同设计条件下的单线圈磁流变阻尼器磁感强度提升了69.03%,标准差降低了86.23%,且漏磁更少,响应更快。
(3) 从优化结果上看,运用ASA算法对双线圈磁流变阻尼器进行多目标优化,使得油膜工作面处的磁感强度提高了20.66%,且优化后轴承支撑区域处磁场更加均匀。可见多参数、多目标优化设计能使阻尼器最大程度发挥磁性能,是磁流变阻尼器设计中的重要一环。
(4) 通过进行磁流变阻尼器油膜处磁场测量试验,发现油膜厚度变化为0.05 mm时会使得测量结果在偏离均值约10%的范围内波动,验证了油膜工作面处的实际磁场分布与计算结果同样具有良好的均匀性,且实际磁感强度能使磁流变液达到有效工作区域(至少达到最大屈服强度的94%),满足设计目标。
(5) 适合的电流作用下,磁流变阻尼器可有效抑制转子系统在临界转速附近的振动幅值,且作用电流越大,磁流变阻尼器阻尼力越强,振动抑制效果越明显。与此同时,电流的增强也会使磁流变阻尼器支承刚度增大,从而使得转子系统的临界转速提高。在过大的电流作用下,磁流变阻尼器的刚度效应起主要作用,其会限制磁流变阻尼器间隙中的油膜挤压作用,进而削弱了磁流变阻尼器的阻尼效应。
附录A
由磁路欧姆定律可求磁阻
(A1)
式中:R为磁路磁阻;μ为磁导率;Le为有效工作长度。
则由式(A1)可得图3中各部分磁阻分别为
(A2)
(A3)
(A4)
(A5)
(A6)
(A7)
(A8)
(A9)
(A10)
(A11)
(A12)
式中:μ0,μ45,μDT,μMRF分别为真空磁导率,45号钢相对磁导率,电工纯铁相对磁导率和磁流变液相对磁导率;L0为油膜轴向长度;T为油膜厚度。

