踝关节训练器关节旋转角实时优化方法

赵金凤，刘健欣

（1.平顶山学院，河南 平顶山 467000；2.山东师范大学，山东 济南 250014）

1 引言

踝关节训练器作为踝关节功能恢复的专业训练器械，可有助于患者踝关节损伤的恢复，其适用范围包括韧带损伤、关节病变、肌肉损伤、骨折以及神经系统病变等。踝关节训练器的关键器件是关节旋转器，其旋转角度的变化直接影响踝关节的恢复效果[1]。

文献[2]研究了基于Hermite 插值二子样的角增量算法，运用于对制导炮弹的姿态进行估算，该算法虽可应用于制导炮弹的高动态环境，但其在踝关节训练器运动姿态采集中，受过程噪声的干扰导致更新采样频率还有待进一步提高；文献[3]提出了后置处理的旋转角度优化算法，用以解决五轴联动机床的转角受限问题，该算法虽能对旋转角予以修正，但其优化效果并不理想。文献[4]结合踝关节的特点，优选出了一种能辅助实现人体踝关节运动的三转动并联机构，并对其进行了运动学分析。但是该方法仅实现了较好的踝关节辅助运动，未对旋转角度进行抓取和分析。文献[5]提出了基于三子样姿态更新的扩展卡尔曼姿态估计算法，利用当地导航系下重力场，磁场中相关数据通过比例积分控制器完成对角速率误差的一次补偿，同时作为扩展卡尔曼观测信息，完成对姿态四元数的实时校正。但是该算法尚未应用于踝关节训练器旋转角度采集优化中，其性能有待进一步分析。

为提高踝关节的康复效果，使之快速恢复健康状态，因此，这里提出了踝关节训练器旋转角度实时优化方法，其目的是通过实时优化关节旋转角度，保证踝关节训练器的安全使用，从而实现背屈及内、外翻等多方向、多角度训练，提高训练效果。

2 踝关节训练器运动原理

踝关节主要由胫骨、腓骨下端的关节面与距骨滑车构成，当其运动时，主要负责脚部的背屈运动，距下关节带动脚部的内外翻运动，当距下关节受到伤害导致不能活动时，踝关节可起到弥补作用，带动脚部完成内外翻动作，但会限制跟部的活动范围，当踝关节受到伤害时，距下关节将协助其完成跖屈和背屈动作。因此，在脚部运动过程中，两个关节既要协作运动，相互间又可以作功能弥补。脚部运动模型和踝关节训练器示意图，如图1所示。

图1 脚部运动模型和踝关节训练器示意图Fig.1 Schematic Diagram of Foot Motion Model and Ankle Trainer

图1所示的踝关节训练器的主要构件包括支座、脚踏板、关节旋转器、加速度传感器、固定装置、动力传动装置[6−7]等。其中，内旋或外旋训练时，通过脚踏板下安置旋转器实现，并利用加速度传感器采集旋转角，确定训练器的旋转器位置，使之与脚内、外踝的连线基本重合，使用动力装置驱动脚部的非自主训练。

内翻和外翻训练时，首先将患肢和脚分别放于托架和鞋托上，并用粘扣固定，手握挟手做拉松的动作，动作要逐渐由小到大、由弱到强。背屈或跖屈时，利用机械传动原理设置传动装置，使训练器完成背屈或跖屈动作，通过训练器中的固定位置防止踝关节背屈结束向跖屈转换的时候，跖屈过度，造成损伤。

三组训练中内旋或外旋训练可以单独完成，但是内翻和外翻以及背屈或跖屈两组动作不能独立完成，因此，踝关节训练器通过两个动力源及独立的传动装置将两组动作分离，在训练器的支座上安装背屈结构，在背屈运动的控制器件上安装内外翻运动器件。

3 踝关节训练器关节旋转角度优化

为了实现踝关节训练器关节旋转角度实时优化，利用卡尔曼滤波算法对踝关节训练器运行状态进行估算，并使用加速度传感器获取的观测数据对关节旋转器获取的预测数据进行修正，实现数据的融合，完成踝关节训练器关节旋转角度优化。

3.1 卡尔曼滤波算法原理

当无法测量实际运行态势时，可通过卡尔曼滤波算法对其运行状态进行估计运算，获得最小的估计均方误差，使状态估计结果最接近于实际状态[8]，达到优化的目的。设定x∈Rn为基于离散时间过程的初始阶段，时间过程的表达式为：

设定z∈Rm为预测变量，量测方程可表示为：

式中：xk—k时刻的运行状态；zk—测量值；F—xk−1对xk的增益函数；H—xk对zk的增益预测函数；λk—任意信号的过程噪声；μk—预测噪声。设定λk、μk是高斯白噪声，呈现正态分布，且互不影响。将其描述为：

式中：Q—过程噪声的协方差函数；R—预测噪声的协方差函数，提升滤波器的效果可将Q、R作相应改变。假设为xk的先验估计的概率分布对的变化起决定作用，基于离散时间过程，其状态变量表示为：

式中：Pkˉ—k时刻的误差协方差函数。

3.2 基于卡尔曼滤波的关节旋转角度实时优化

预测数据采用踝关节训练器中的关节旋转器的测量值，观测数据采用加速度传感器的测量值，基于卡尔曼滤波算法使用加速度传感器获取的观测数据对关节旋转器获取的预测数据进行修正，实现数据的融合[9]。

设定β(k)为关节旋转器的角速度误差，G_ω(k)为关节旋转器的输出角速度，ω(k)为关节旋转器k时刻测量的角速度，G_ω(k−1) 为前一刻的角速度，角速度误差与此刻角速度及前一刻角速度相关，可表示为：

关节旋转器的静态勘测性能不显著，是由于其具有漂移误差[10]，相反，静止状态下，加速度传感器的勘测性能优越，其当前时刻获取的角速度为J_g(k)，该值可替换关节旋转器获取的角速度G_ω(k−1)，关节旋转器角速度误差可描述为：

式中：G_ω(k)—第k时间点关节旋转器获取的角速度；J_g(k)—加速度传感器输出的角速度；β(k)—误差。系统预测方程的表达式为：

关节旋转器的旋转角预测值可根据式（8）、式（11）予以修正，可将其表达为：

式中：Ang1_f(k)—k时刻经修正的旋转角，k时刻的最优估计值L(k|k)可通过运算获得，再计算获得估计均方误差方程，使卡尔曼滤波器得以循环运行，该方程可描述为：

采集关节旋转器k+1时刻的输出信号后，返回计算该时刻的滤波，实现关节旋转角度实时优化。

4 实验分析

为分析踝关节训练器的关节旋转角度优化问题，设置一踝关节训练器，并安装关节旋转器和加速度传感器，关节旋转器的预测数据传输给计算机1，将加速度传感器连接在一个采集数据仪器上，获取加速度传感器的测试数据，并将其输出在计算机2的显示屏上。通过MATLAB软件模拟卡尔曼滤波器，用计算机2获取的数据修正计算机1的输入数据，实现数据的融合。

4.1 实验准备

实验过程中，以频率为0.8Hz、角速度为5rad/s、加速度为15rad/s作为踝关节训练器的输入参数，测定关节旋转器实时优化下的预测数据及加速度传感器的测量数据，并根据所提方法进行数据融合，测试踝关节训练器的关节旋转角度。踝关节训练器关节旋转角度实时优化下输入和输出波形，如图2所示。

图2 关节旋转器波形图Fig.2 Joint Rotator Waveform

分析角速度输入输出曲线可知，踝关节训练器旋转角速度输出曲线在波峰处有较多的波动，曲线光滑程度下降，曲线波动范围为±5.3之间，具有较大的偏差。采集数据仪器获取的加速度传感器的角速度的输出波形，如图3所示。

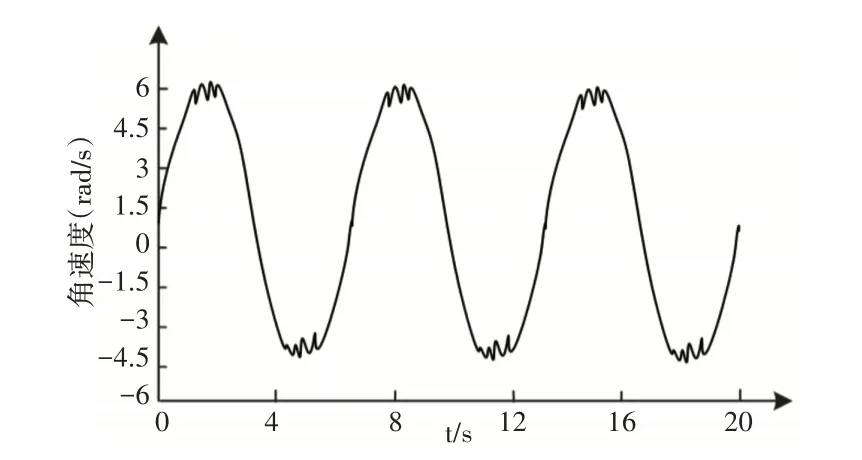
图3 加速度传感器的输出角速度波形图Fig.3 Output Angular Velocity Waveform of Acceleration Sensor

分析图3可知，同一条件下测得的加速度传感器角速度输出值为4.97rad/s，与设定的踝关节训练器的角速度输出值5rad/s的误差较小。因此可用加速度传感器输出值修正关节旋转器输出值。

以上述的实验参数设置为基础，采用所提方法，文献[2]的基于Hermite插值的旋转角度优化方法、文献[3]的后置处理的旋转角度优化方法对关节旋转角度进行动态优化，分别通过收敛精度和关节旋转器的磨损程度两项指标验证所提方法的优化性能。

4.2 关节旋转角度收敛精度测试

关节旋转角度收敛精度测试通过式（5）得到的后验状态估计值反映，该值为关节旋转角度量测值的估计值，该值越高，表示关节旋转角度收敛精度越高，踝关节训练器的训练稳定性越高。因此，利用三种方法优化关节旋转器的旋转角度，得到收敛结果，如图4所示。

图4 关节旋转角度收敛精度Fig.4 Convergence Accuracy of Joint Rotation Angle

分析图4可知，采用三种方法进行旋转角度优化，所提方法的后验状态估计值高于其他两种方法，可达到0.9以上，文献[2]方法次之，文献[3]方法的收敛精度最低，因此，采用所提方法优化旋转角度具有显著效果。

其主要原因是所提方法采用卡尔曼滤波算法融合关节旋转器与加速度传感器数据，修正关节旋转器获取的预测数据，提高了旋转角度优化精度。

4.3 关节旋转器磨损程度测试

优化关节旋转器的旋转角度后，为了优化康复训练效果，使用式（14）所示的经修正的旋转角预测值，检验关节旋转器的磨损程度。修正的旋转角预测值与旋转角初始值差值越小，表示关节旋转器的磨损程度越低，测试结果，如图5所示。

图5 关节旋转器的磨损情况Fig.5 Wear of Joint Rotator

分析图5可知，随着使用时间的增加，所提方法优化后的关节旋转器的磨损程度最低，说明所提方法能使关节旋转器受到较小的摩擦，更有利于关节灵活旋转，体现出踝关节训练器经关节旋转角度优化后具备更佳的使用性能。而文献[2]方法、文献[3]方法优化后的关节旋转器，磨损程度较高，应用性能较差。

5 结论

为了保证踝关节的恢复效果，这里通过设定踝关节训练器参数，分别测试动态下关节旋转器、加速度传感器的角速度输出值，并利用提出方法通过融合关节旋转器和加速度传感器的输出数据完成旋转角度动态优化。

测试结果表明两者单独使用时测试数据存在一定的偏差，通过所提方法优化后，可使关节旋转器的旋转角度输出值更精确，关节旋转角度优化效果显著。利用不同方法优化踝关节训练器关节旋转角度后的测试结果表明，所提方法优化的收敛精度更高，且关节旋转器的磨损程度更小。