金属薄壁结构在高速流动下热声响应特性分析方法

沙云东，艾思泽，张家铭

（沈阳航空航天大学航空发动机学院 辽宁省航空推进系统先进测试技术重点实验室，辽宁 沈阳 110136）

1 引言

随着现代飞行器性能的逐渐提升，给航空发动机的性能要求和结构设计带来了很大的挑战。超高音速飞行器结构在工作时承受复杂的机械力载荷、气动力载荷、热载荷和强噪声载荷[1]。其中，在高速飞行中，薄壁结构不仅承受流动载荷带来的随机声激振力，还承受高温环境带来的热应力，材料参数与结构强度都会发生变化，使结构表现出复杂的大扰度非线性响应，严重影响薄壁结构的使用寿命，导致疲劳失效，对航空发动机的结构完整性和整体可靠性产生严重威胁。针对这种情况，十分需要一种处理薄壁结构在高速流动下热声载荷问题的分析方法。

目前对于热声载荷作用下结构非线性应力响应问题的数值计算方法主要包括：摄动法（Perturbation）、FPK 方程法、蒙特卡罗法（Monte Carlo）、伽辽金法（Galerkin）、等价线性化方法（EL）、有限元法（FEM）、耦合有限元/边界元（BEM/FEM）法等。国外对热声问题研究较早，在大量的试验与理论研究的基础上对热声载荷作用下薄壁结构动力响应开展深入研究。文献[2]通过大挠度方程与伽辽金法计算研究了薄壁结构在热后屈曲的响应。通过蒙特卡罗法和伽辽金法，文献[3]深入计算分析了在噪声环境下的结构振动响应。文献[4]通过等效线性法和伽辽金法，深入分析了薄壁结构在声载荷和热载荷联合作用下的响应特征，并且通过数值仿真得以印证。文献[5]将有限元法和等效线性法结合应用在热声载荷联合作用下的梁结构，发现结构热屈曲后模态振型产生变化。

国内，文献[6]使用有限元−统计能量方法得到材料物性与热应力对结构模态频率的影响，并分析出高温环境中165dB声压级下结构声振特性。文献[7]从单、双向耦合研究了流−热−固多场耦合问题，讨论了耦合分析的发展趋势，但未进行试验验证。文献[8]从能量角度分析了航空发动机燃烧室热声耦合产生的根源及作用机理。文献[9]结合气动热和结构传热建立了热流固耦合力学模型。文献[10]针对航空薄壁结构的热声疲劳问题，结合大量数据采用耦合的有限元及边界元法（FEM/BEM）、薄壁结构大挠度方程以及薄壁构件热屈曲理论等相关理论方法研究了大量航空薄壁结构的非线性动力学响应分析。以上文献或缺少有效试验验证，或探究以热声载荷形式对薄壁结构动力学响应影响，未体现航空发动机薄壁结构工作中所承受高速流动作用下热声响应的变化与影响。

薄壁板在高速气流下的振动问题都是气动弹性稳定性的问题，为了简化分析与计算，采取简化处理：首先，通过对流场与结构场耦合分析，得到在高速气流下薄壁板所受的压力载荷、温度载荷，利用耦合边界元/有限元法加载声载荷，得到结构应力应变响应，然后，将简化后的结构所受的声载荷、热载荷与应力载荷模型通过控制变量法，在其变化范围内进行分析，得到薄壁板的应力响应规律。将热声数值仿真计算结果与热声试验结果进行对比验证，证明了热声仿真计算分析方法的可靠性与可用性。并在相同热载荷和声载荷作用下加载高速流动，与热声仿真结果进行对比分析，分析高速气流对薄壁结构动力响应的影响。

2 多场耦合理论分析

2.1 流体相关理论

流场采用有限体积法分析。流体运动控制方程为三维可压缩的Navier−Stokes方法，方程如下：

（1）质量方程

其中，左边首项为密度变化率，如果相关气体为不可压缩流动时该项为0。第二项为质量流密度的散度，公式右边的源项Sm−稀疏相增加到连续相中的质量变化量。

（2）动量方程

式中：p—静压；τij—应力张量；ρgi—重力体积力；Fi—其他体积力（如来源于两相之间的作用力）。

（3）能量方程

其中，方程右侧括号内三项分别为流体导热项、组分扩散项和粘性耗散项，keff=kt+k—流体有效导热系数；Jj′—组分；j′—扩散通量；Sh—包括化学反应热或其他体积热源项。

（4）湍流模型

进行流体动力学计算时只是满足三大守恒方程，方程组并不封闭，无法进行求解。湍流模型应在三大守恒方程的基础上配合使用方程组才可求解。使用的标准k−ε湍流模型，也是计算流体动力学中最常用的湍流模型之一。标准k−ε模型由2部分组成，湍动能k方程和湍流耗散运输方程ε方程如下：

式中：Gk—由层流速度梯度引起的湍动能项；Gb—浮力产生的湍动能项；YM—在可压缩流动中湍流脉动膨胀到全局过程中对耗散率的影响项；C1，C2，C3—常数；σk、Sk—式（4）k方程的湍动能项和湍流普朗特数；σb、Sε—式（5）e方程的湍流普朗特常数和湍流耗散源项。

2.2 薄壁结构大挠度控制方程

在多物理场复杂载荷环境下，薄壁板动态响应是典型的大挠度弯曲振动响应。采用Von Karman薄板大挠度理论和Kirchhoff的相关假设对应变位移关系进行微分运算可以得到挠度表示的应变协调方程，如下式：

引入Airy应力函数F表示薄膜应力，得到应力函数表示的应变协调方程，如式（7）：

式中：应力函数F=Fh+Fp—待求解的未知函数，由特解Fp和齐次解Fh组成；w—板的挠度函数。

将应力和对应剪力、薄膜力、弯矩，考虑阻尼力、声载荷、惯性力，对板进行受力分析，可以得到包含温度项的Von−Karman 大挠度运动方程：

式中：ρ—密度；ξ—阻尼系数；μ—泊松比；D—弯曲刚度；∇4—双调和算子；p(x，y，t)—模拟声载荷的随机压力。

2.3 热流固耦合控制方程

热流固耦合理论是由流固耦合理论发展而来，在流固耦合理论中，温度场假设为恒定，或不考虑流体流动和薄壁板变形与温度场变化之间的耦合作用。实际情况下，航空发动机中存在剧烈的温度场变化，并且高温对薄壁结构的作用是不容忽视的，热应力导致的热屈曲会改变材料参数和结构强度。所以，进行热流固耦合研究是十分必要的。

稳态时薄壁板气动载荷值为表面压强值，故薄壁板流固耦合数值分析可化为静力学求解。应用结构有限元法数值计算应力{σ} 和单元节点位移{δ}的方程如下：

式中：[K]—刚度矩阵；{P}—结构表面压强值；[B]—几何矩阵；[D]—弹性矩阵；[H]—微分算子矩阵；[N]—单元形函数。

结构传热控制方程可以描述为：

式中：(C){}—热量沉积项；λ—导热系数；{Q} —整个系统热能。

联合传热方程和流固耦合数值计算方程得到能量方程如下：

式中：Ue—单元弹性能；εE—弹性应变矩阵；ε—总应变矩阵；εT—热应变矩阵；D—单元弹性矩阵。故将方程（11）代入方程（12）中得到热载荷下结构控制方程，如式（13）所示：

式中：{FT}—气动热载荷矩阵。

再结合气动力载荷矩阵{FP}得出热流固耦合的控制方程如下：

2.4 基于FEM/BEM法耦合理论

对于声载荷的影响，可以采用边界元法将流体域的声场进行离散化处理，计算流体域的声压和振动速度，采用有限元与边界元耦合的方法分析声载荷下的结构动力学响应。

在声波和固体结构间的交互作用的相关内容中，克希霍夫−亥姆霍兹积分方程阐明了某任意物体上表面振动谐运动与周围流体中辐射声压场的关系，如式（15）所示：

结构在温度场与压力场耦合下的模态与声模态叠加，采用这种弱耦合的方式，可以求解结构在热声流固耦合下的模态和应力应变问题。在声载荷作用下，声压和模态位移之间的关系，如式（16）所示：

式中：Hpact—声传递函数；ua(t)—边界声场质点位移。结合边界元法中声场控制方程，可以得到一种声传递函数的表达式，如式（17）所示：

式中：[H]和[G]—影响矩阵；[LT]—传递矩阵，用于传递声载荷，从边界单元的中心到有限单元各节点。

对结构施加声载荷功率谱密度SIN(ω)，得到模态应变位移谱密度(Sd(ω))n：

对结构有限元、声学边界元通过频域进行谱密度耦合，未知量为有限元结构模态应变位移谱密度和边界元声压谱密度。即耦合有限元/边界元的结构动力学控制方程为：

式中：CPLG(ω)—全耦合矩阵；SDr(ω)—结构动力响应功率谱密度函数；SDIN(ω)—外部激励功率谱密度函数。

3 热流声固耦合作用下薄壁板响应分析方法

3.1 高速流动下热声响应分析

采用高温合金GH188四周固支简化薄壁板为研究对象，材料性能，如表1所示。加入高温高速气流，在不同流速不同温度下行波加载噪声激励，薄壁板将承受高温载荷和高速流动下产生的气动力及噪声载荷的联合作用，研究热流声固耦合下动力学响应，分析不同温度载荷和流动速度下影响结构响应的主要因素。结合航空发动机典型工况，给定流速，温度，声压级组合，如表2所示。计算薄壁板响应。

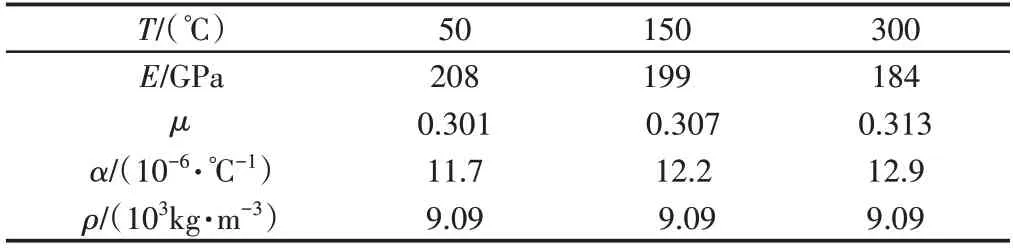
表1 GH188材料属性Tab.1 Material Parameters of GH188

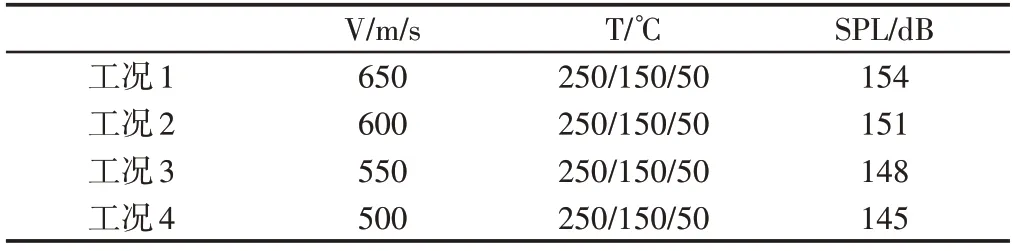
表2 薄壁板加载工况Tab.2 Loading of Thin-Walled Plate

流体仿真模型，如图1所示。采用双面受流的方式，流体域左端定义为速度入口，右端定义为压力出口，采用有限元法对流体域声场和压力场进行计算，仿真计算采用k−ε湍流模型。

图1 流体仿真示意图Fig.1 Fluid Domain Simulation Diagram

薄壁板在不同流速下冲击力载荷分布，如图2 所示。流速为100m/s时薄壁板所受最大载荷为2711.53Pa，薄壁板主体所受载荷为11.5Pa；流速为250m/s时，薄壁板所受最大载荷为17362.0Pa，薄壁板主体所受载荷为94.5Pa；流速为500m/s时，薄壁板所受最大载荷为22603.4Pa，薄壁板主体所受载荷为267Pa；流速为650m/s时，薄壁板所受最大载荷为38341.8Pa，薄壁板主体所受载荷为413.6Pa。综上可知，薄壁板所受冲击力载荷随着流速的增加而增大。

图2 薄壁板在不同流速下冲击载荷分布Fig.2 Impact Load Distribution at Different Flow Rates

薄壁板热流冲击下温度分布，如图3所示。观察可发现，相同温度不同流速下，流速越大薄壁板表面温度分布更集中，温差更小且最高温度更大，因此，随着流速的增大温度载荷对薄壁板的影响更加明显。

图3 薄壁板在不同热流冲击下温度分布Fig.3 Temperature Distribution Under Heat Flow Shock of Thin Wall

计算得到薄壁板在50℃，150℃，250℃热模态基频分别为263Hz，320Hz，473Hz。在流速100m/s，温度为50℃，声压级为75dB情况下薄壁板应力云图，如图4所示。相同温度下薄壁板受力分布一致，相同流速下薄壁板所受声压级一致，所以温度直接影响薄壁板的应力载荷的分布。观察发现，危险点均出现在薄壁板短边中点，温度为50℃时最大应力值为9885Pa，温度为250℃时最大应力值为16850Pa，随着温度的升高，最大应力值增大，可知温度载荷对薄壁板应力响应有很大的影响。

图4 薄壁板应力分布示意图Fig.4 Stress Nephogram of Thin−Walled Plate

在流速为650m/s，温度载荷为150℃及声压级为154dB情况下，薄壁板各个方向的最大应力频域分布，如图5所示。可发现X轴正方向应力值远大于其他各轴应力值，因此主要研究X轴正应力即可。

图5 薄壁板各方向应力值对比Fig.5 Stress Contrast of Thin Wall in all Directions

相同流速不同温度下应力功率谱密度对比，如图6所示。

图6 薄壁板在不同温度下应力PSD值对比Fig.6 Stress PSD Comparison of Thin−Walled Plate at Different Temperatures

各工况下应力响应基频与热模态基频保持一致。随着温度的升高，峰值向左移动。相同温度下不同流速应力PSD对比，如图7所示。温度载荷一致，薄壁板响应频率一致，同一频率出现最大载荷。且由于流动的影响，随着流速的增加，大频率处会出现一定的变化。

图7 薄壁板在不同流速下应力PSD值对比Fig.7 Stress PSD Comparison of Thin−Walled Plate Under Different Flow Rate

3.2 热声试验响应分析与验证

3.2.1 热声载荷作用下结构响应试验

由于高速流动下热声试验的复杂和困难性，于是针对高温合金GH188薄壁板，首先开展无流速下热声响应试验。试验件板厚1.5mm，长宽尺寸，如图8所示。并分别在长短边中点安装应变片，短边中点的#1和#3用来测量x方向的应变，长边中点的#2和#4用来测量y方向的应变。

图8 薄壁板模型尺寸Fig.8 Geometry Model of Thin−Wall Plate

试验件安装在行波管侧壁上，通过一个口框夹具压紧试验件，采用双排螺栓拧紧方式对试验件四周固定，如图9所示。

图9 试验件安装Fig.9 Installation of Test Piece

在试验夹具中通入流动的冷水对试验夹具降温，试验件和试验夹具之间采用隔热材料，减少试件与夹具之间的热传导。在平板试验件的两侧各布置一个加热灯箱，通过两个石英灯管对试验件表面进行双面加热，温度为（50～250）℃，间隔为50℃，行波管通过掠入射方式加载噪声载荷到试验件，频率范围为（100～1250）Hz，声压级范围为（145～154）dB。采用激光测振仪进行加速度监测，加速度测点位于试验件一侧的中心位置，如图10所示。由于结构在一阶固有频率处最大峰值，因此可以测得结构一阶频率。试验目的为获取薄壁结构在高温、噪声条件下振动应变响应，该试验系统完全可满足试验要求，在高温载荷和试验载荷的联合加载下，得出一系列响应结果，并能分析总结出温度及声载荷变化规律。

图10 试验仪器Fig.10 The Test Instrument

3.2.2 热声仿真计算对比验证

通过仿真计算，得到薄壁板在不同温度下的前6阶热模态频率，如表3所示。通过计算得到薄壁板热屈曲温度为98.9℃，可观察各温度下基频的变化特征，从（50～100）℃，基频减小，之后随着温度升高，基频不断增大，且不同温度下同阶频率都符合这一变化规律，进一步验证了薄壁板的热屈曲温度为100℃附近。

表3 薄壁板在不同温度载荷下前6阶热模态频率Tab.3 The First 6 Order Thermal Modes of Thin-Walled Plate at Different Temperatures

通过激光测振仪可得到结构基频，如图11所示。

图11 试验件中心点加速度响应结果Fig.11 Acceleration Response Results at the Center Point of Test Piece

加载温度为50℃时试验件中点加速度响应，从中提取峰值处频率，整理与仿真一阶频率进行对比，如表4所示。对比分析可知薄壁板一阶固有频率仿真值如实测值最大误差为1.5%，表明两者一阶固有频率具有一致性。

表4 薄壁板在不同温度下热模态基频与试验结果对比Tab.4 First Order Natural Frequency/Hz of GH188 Test Piece at Different Temperature

通过薄壁板长短边安装的应变片，可获得薄壁板在X轴与Y轴方向的应变响应，试件在温度为100℃和噪声载荷为151dB环境下的X轴应变频域响应结果，如图12所示。薄壁板在此状态下最大应变值为18.7με。整理数据与仿真结果，将最大应变值进行对比验证，如表5所示。结果表明，仿真应变响应结果与试验数据十分吻合，验证了在热声载荷联合作用薄壁板的动力学响应仿真计算方法的可行性。

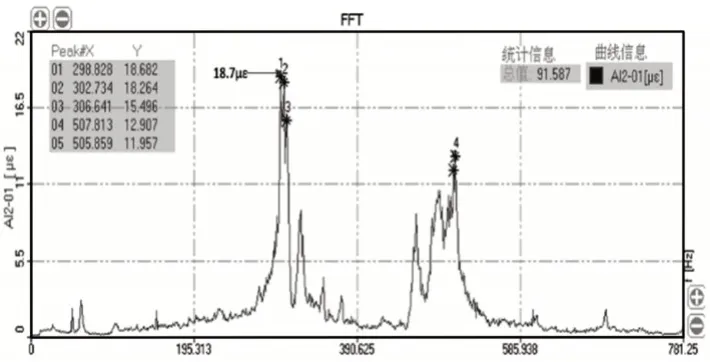
图12 试验件X轴应变频域响应结果Fig.12 Frequency Response Results of X−axis Strain

表5 薄壁板测点位置多方向最大应变值对比Tab.5 Maximum Unidirectional Strain of Measuring Point Location Unit

以上通过对比验证了薄壁板在高温环境下热模态频率，以及在高温载荷和噪声联合作用下薄壁板最大应变响应，充分验证了热声载荷作用下薄壁结构仿真计算方法的可行性及有效性。

3.3 高速流动对薄壁结构热声响应的影响

为了分析说明高速流动对薄壁结构热声动力响应的影响，薄壁板分别在有高速流动和无高速流动的作用下加载相同温度载荷和声压级载荷，为了凸显高速流动对结构动力响应的影响，加载相对较低的温度载荷，加载分布加大的声压级载荷，得到有/无流动下热声响应结果进行分析研究，探索高速流动对薄壁结构的影响作用。

得到薄壁板X轴应变频域响应，如图13所示。观察发现，薄壁板在有高速流动时均比无流速下产生更大的应变。在不同流速下，薄壁板X轴最大应变值，如表6所示。在温度150℃声压级为160dB下，无流速下最大应变为0.16ε，作用流速200m/s下最大应变为0.37ε，充分说明高速流动产生的气动力载荷对薄壁板响应有不可忽视的影响。并且在高声压级与流动共同作用下，薄壁板动力响应会更加明显。

图13 薄壁板在有/无流速下应变频域曲线对比Fig.13 Comparison of Strain of Thin−Walled Plate with or without Flow Velocity

表6 薄壁板在有/无流速下最大应变值对比Tab.6 Comparison of Strain of Thin-walled Plate with or without Flow Velocity

4 结论

（1）针对薄壁板在高速流动下热声动力响应问题，采用有限体积法对薄壁板双面加载高速气流，得到薄壁板在高速气流作用下冲击力载荷分布，采用有限元法进行固体计算，得到不同流速和不同温度下薄壁板温度分布，利用耦合边界元/有限元法进行噪声载荷行波加载，得到薄壁板在热声流多场耦合下各方向应力应变值；（2）考虑航空发动机实际情况，加载四种典型工况，对比得出X轴正应力为最大应力，且响应曲线峰值频率与薄壁板热模态基频保持一致，相同流速和声压级下，薄壁板随着温度的升高峰值左移。不同流速下，其他载荷一致，响应曲线整体趋势保持一致；（3）针对高温合金GH188四端固支薄壁板热声激励试验进行数值模拟仿真验证，有限元法进行结构受力分析，耦合的有限元与边界元法进行成声场模拟计算，通过不同温度下热模态，X，Y轴应力功率谱密度及最大应变响应数据对比，误差均在工程应用范围内，充分验证了热声仿真模型的有效性。（4）得到薄壁板在高速流动下与无流动下热声载荷应变响应结果直观对比，在流速为200m/s下加载160dB，薄壁板最大应变为0.37，是无流动下的应变值的2.3倍，高速流动带来的冲击力载荷和强噪声载荷联合作用下都对薄壁结构响应都很大的影响。这也是之后需要解决和继续研究的方向。