热声效应及其应用研究进展
李亚清,史学强,张玉涛,杨超萍,张 静
(1.西安科技大学 安全科学与工程学院,陕西 西安 710054;2.陕西省工业过程安全与应急救援工程技术研究中心,陕西 西安 710054)
0 引 言
在可压缩流体介质中(第一介质),热声效应是指时均热流与时均声流通过具有温度差的固体壁(第二介质)相互转化,热声机械就是利用热声效应,实现一般的使用目的。早在200多年前,人们就发现热与声之间的微妙关系,其中,Putnam在其综述提到“歌焰现象”,即将两端开口管的一端靠近燃烧的氢火焰时,开口管会发出像风琴管一样的声音[1]。人们开始定性的研究热声现象,其中比较著名的有Soundhauss管[2]与Rijke管[3],但是这些实验中观察到的振荡很弱,较为强烈的声振荡研究是在Ceperley提出的热声Stirling发动机,他将声波代替传统Stirling发动机的运动部件,在理论上可以达到卡诺效率[4]。1999年,Swift与Backhauss建立的新型热声Stirling发动机能够达到41%的相对卡诺效率,并获得了美国当年的“R&D100”奖[5],这对热声效应的研究产生极大的鼓舞。热声理论的研究于1868年Kirchhoff 由气体与固体管壁的振荡传热计算管道中的声衰减开始[6],之后Rott建立了线性热声数学模型,对热声机械定量的研究有重要的意义[7]。从1990年开始,热声研究集中于非线性热声理论,尤其是研究技术与研究方法的巨大发展带动非线性热声理论的进步,从而可以科学地优化热声机械。
根据热声效应的原理,热声机械可分为热致声的热声发动机和声致冷的热声制冷机[8]。其中,热声发动机通过热能交换激起声振荡;热声制冷机通过声波将热能导出,形成低温区。热声机械结构简单、无运动部件、且完全环保,可以将低品位热能与声能相互转化,在空调制冷与能源动力方面有着极为广阔的应用前景。由于结构紧凑且无源,热声机械也广泛应用于电子散热[9-10]、消防报警[11-13]等方面。应用于不同领域的各种新型热声装置不断涌现,文中对热声效应的相关理论、研究方法与实际应用及已有的热声机械进行了分析与总结,帮助人们更加全面的理解热声理论,为日后热声效应的应用、新型热声机械的研发及优化提供指导与借鉴。
1 热声效应理论
1.1 热声效应定性研究
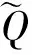
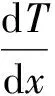
图1 驻波热声发动机示意图Fig.1 Schematic of standing wave thermoacoustic prime mover
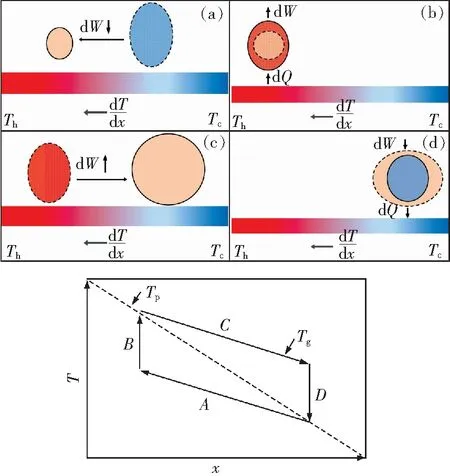
图2 驻波热声发动机热力过程Fig.2 Thermodynamic processes of standing-wave thermoacoustic prime moverTp为板叠温度;Tg为小气团温度;Th为板叠高温端温度;Tc为板叠低温端温度
1.2 热声效应模型
1.2.1 线性热声理论
自从20世纪60年代Rott根据Taconis振荡以动量方程、质量方程以及能量方程为基础,以固体为热声边界建立了理想驻波声场方程(Helmholtz方程)后,热声效应开始有了数学模式的定量描述[15],其二阶微分波动方程为
(1)
Rott方程研究了气体参数、压力与温度之间的关系,是热声发展史上的第一次完整的数学描述,对热声理论的定量研究具有深刻意义,之后的相关线性数学模型基本都是Rott小振幅线性模型的改进与拓展。
近年来,随着越来越多热声效应的实验研究,线性热声理论不断完善,其中Swift短板叠边界层近似理论对经典线性理论的补充最为重要,Swift理论主要强调3点:①板叠长度与装置相比极小,对声场影响不大;②板叠热容很大,流体的振荡对其温度影响很小;③板叠纵向的导热可以忽略[16]。同时,Swift提出了“临界温度”的概念,其表达式如下
(2)
式中A为板叠横截面积;U1为振荡体积流率。
对于非粘性的流体介质,当驻波热声发动机运行时,温度梯度应满足|dTm/dx|>Tcrit,当驻波制冷机运行时,温度梯度应满足|dTm/dx| 1.2.2 非线性热声理论 由于热声机械中复杂的非线性温度场分布以及非等温涡流,线性热声理论在自激振荡以及低频高振幅热声转化中显示出很大的局限性,而非线性理论能解释热声的能量耗散现象,当前的热声理论研究主要集中在热声的非线性方面,采用有限元模拟软件(Comsol Multiphysics 5.2a)模拟得到板叠端非线性速度场与温度场,如图3所示,速度场中颜色表示速度大小(m/s),箭头为速度矢量(m/s)、温度场中颜色表示温度大小(K),箭头为热通量矢量(W/m2)。 图3 热声振荡过程板叠出现的非线性现象Fig.3 Nonlinear phenomena appearing in the stack during thermoacoustic oscillation Worlika等通过数值模拟的方法建立了热声制冷机的低马赫数的不稳定可压缩模型,定性定量的研究了非线性涡流的运动特征、声共振波振幅对温度梯度的影响以及板叠结构对能量的作用,同时还建立了一个非线性时域的准一维近似声学方程[17-18]。以Rijke管的非线性热声振荡为基础,韩飞等根据质量、能量以及动量三大守恒方程以及管口的非线性反射推导出热声振荡由小扰动增长到大振幅,以及能量耗散导致衰减结束的整个过程的方程,还发现非线性效应限制了管内声波振幅的发展,并且导致二次谐波[19]。Hamilton等对热声不稳定性进行大量算法研究,通过快速改变板叠中的空间导数,得到了热声发动机非线性效应的二维模型和有效解[20-21]。Gong等采用数字全息技术测量板叠温度梯度处的气体密度振荡,实验结果表明温度梯度影响了气体密度振荡的幅度,气体密度波动在板叠处由于入口效应而高度扭曲,将基于入口效应描述的理论结果与实验进行比较,结果显示出良好的一致性,再次确认了板叠附近的温度与密度振荡的高度非线性[22]。Kazuto Kuzuu等通过CFD模拟发现了换热器周围涡流的高能耗以及不均匀温度梯度,其结果显示换热器内出现不对称的温度振荡[23-24]。Los Alamos国家实验室研发了一系列热声机械,在其实验过程中总结了与经典线性理论不一致的现象(例如质量流、声流),并对其作出了一些定性的描述。 1.2.3 其他热声理论模型 此外,随着热声理论的不断发展,各种理论相继被提出,涉及线性以及非线性的特性,文中在表1中对其各自的适用条件及局限性进行了归纳。 表1 其他热声理论模型Table 1 Other thermoacoustic theoretical models Soundhauss通过对一端开口管(图4(a))的闭合处加热,发现声音不是由管子的振动引起,并且声音的高低只与器皿的容量呈一定的规律[2]。Rijke将热丝网置于管下半截(图4(b))时,管发出声音,当丝网位于1/4处效果最好,实验过程中的声音是不稳定的音调[3]。Taconis发现当一端开口管的开口端置于低温液氮表面时(图4(c)),管内会出现声振荡[25]。这些实验与现象对后续的理论研究及工业应用奠定了重要的基础。 Napolitano等分析了用开孔泡沫制作的板叠的热声性能,研究了孔结构对驻波热声发动机内的功率转换的影响,并研发优化算法以获得最大化热声驻波发动机性能的工作频率,管道和堆叠长度[26]。Alcock等研究了一种新的可调节TADTAR(热声驱动制冷机)原型装置,改变装置的实验参数以计算设备的COP值,其结果得到,可调谐振器能成功地改变热声发动机的频率输出,使其与热声制冷机所需的频率相匹配,从而实现谐振,并且单个器件可以具有不同的工作点,这提供了引入控制系统的可能[27]。Yahya等介绍了评估驻波热声制冷机中板叠层热性能的实验方法,测试了不锈钢丝,铜丝和预成形的网状玻璃碳泡沫等堆叠材料,结果表明,rh/δk为2.0和1.1的不锈钢板叠能达到最大的冷却功率,最低的温度以及最高的COPR值,Mylar板堆叠显示出更好的性能,它实现了最大的COP,COPR和温差分别为0.217,0.15%和7.7 ℃[28]。 图4 热声效应的典型实验Fig.4 Typical experiments of thermoacoustic effect 随着基础物理学仪器的进展,热声实验变得越来越可视化。LDV(开普勒测速技术)是一种高精度的非接触式速度场测定仪器,Yazaki最先使用LDV进行热声实验,在板叠处使用透明的玻璃实现可视化,通过测量的数据计算得到声功分布,发现驻波与行波同时存在于2种热声发动机中[29]。Moreau通过LDV测量谐振管中的涡流速度变化,发现板叠的位置变化会改变涡流的状态[30]。 PIV(粒子成像速度仪)可以不干扰流场而得到流动区域的速度场、涡流场变化,可以清楚表征湍流状态,Jaworski等使用PIV对振荡状态的平行板叠的入口效应进行观测,发现在板叠周围出现了非常复杂的非线性涡流现象[31]。Aben等使用PIV对平行板叠内到板叠开口处的流体运动进行研究,使用无量纲数St与Re将旋涡分为双涡、四涡、过渡区以及涡街形式,并用St与Re的比值表示板叠开口处的涡流模式[32]。PLIF(平面激光诱导技术)是PIV技术基础上的一个附加产品,可以定量的对流场的热传递进行测定,Shi等通过PLIF与PIV组合进行二维温度和速度场测量,得到声周期中20个阶段的速度和温度场分布,结果表明惯性、粘性以及热效应对时域局部温度和速度的分布有较大的影响,并发现了温度与速度的过冲现象[33]。 FLIR(红外热像技术)通过收集热辐射绘制成热图像和温度值图像。为了研究亥姆霍兹共振器对行波热声发动机起振的影响,王波首先将FLIR应用到热声研究中,发现亥姆霍兹共振器在起振时刻降低了压力振幅,并增加了热声发动机的起始温度[34]。 HWA(热线风速仪)可以测定流场变化,其实验装置较简化,Mao等使用热线风速仪检测板叠后涡流脱落的速度波动,从而获得St数的变化特征[35]。Shi等改变板叠几何(板叠厚度和间距)和声驱动(驱动比Dr),采用热线风速仪测量技术检测板叠后涡流速度,得到了Re数在200~5 000之间时St数与Re数之间的相关性[36]。 Babaei等开发了用于综合设计和优化热声装置的算法,其算法可以设计持续制冷的热声制冷机[37]。Trapp等设计了一种新颖的数学编程模型,以优化简单热声热机的性能,可以测量多个热学与声学因素(输出功率、粘性损失与热损失),同时可以优化多个目标组件,生成Pareto最优解的有效边界[38]。为了简化整个发动机的可压缩模拟过程,Hireche等开发小马赫数模型,将谐振器中的一维线性声学与小马赫数粘性以及板叠部分的流动(二维数值模拟实现)耦合,成功的捕捉到了热声起振的动态特性[39]。 为了更有效地研究热声效应以及进行热声优化,相关研究人员开发出了一系列热声软件。美国Los Alamos国家实验室Swift等根据改进的Rott线性热声理论编制了一套计算机软件程序DeltaEC,DeltaEC主要采用一维声近似,对波方程与能量方程进行数值积分,能够计算比较复杂的热声机械[40]。郭方中基于热声网络系统模型建立了实用热声网络计算软件TANetwork,可以对网络阻抗、板叠性能、声场和相位进行计算[41]。 理论模型阻碍着非线性因素的表达,无法捕捉到热声系统的非线性效应(板叠区域的湍流,温度的非线性分布),随着CFD(计算流体力学)的发展,由于运行简单、成本低、结果可视化的优点,CFD被广泛应用到热声转换研究领域。Nijeholt等利用CFD(CFX4.4)软件对拓扑变化为二维的Stirling热声发动机模型进行模拟,在结果中发现了线性理论捕捉不到的非线性质量流与涡流,为高振幅研究提供了非线性依据[42]。余国瑶使用CFD软件Fluent对热声发动机进行二维轴对称模拟,研究了边界条件、初始条件与离散格式对CFD模拟结果的影响,在模拟结果中发现了高次谐波以及环路直流,并在模拟中成功的使用风扇模型抑制了质量流,其模拟结果数值上显示了热缓冲管和其他部件中涡流的多维效应,充分表明CFD研究的有效性[43]。Skaria等对驻波热声发动机在不同的平均圧力与工作流体中的工作状态进行了CFD(Fluent 6.3.26)模拟,将其结果与DeltaEC模拟结果以及实验结果进行比对,结果表明压力与流体种类对热声装置的性能有着重要的影响,而且CFD比DeltaEC模拟更加接近实验结果[44]。Zink等使用CFD(Fluent 6.3.26)建立了一个延伸的冷却板叠,并对声波驱动板叠间工作气体的冷却状况进行说明,之后,探讨了谐振器曲率对热声效应的影响,发现曲率的引入会影响压力幅度与工作频率[45-46]。Rogoziński等通过对比数学分析与CFD模拟(CFX)的差异,发现了板叠附近的湍流现象[47]。Belaid等使用数值方法研究热交换器板间距对热声制冷机(TAR)性能的影响,测试了热交换器板间距的几种几何布置,结果与DeltaEC软件提供的结果一致,较低的换热器堵塞比降低了涡流的尺寸和效果,并提供了更好的制冷效率[48]。 刘旭和陈宇等将温度场引入9 bit格子气模型中,模拟了板叠长度与板叠位置对声波幅度的影响、自激振荡的变化过程与回热器的优化,结果证明格子气法适用于热声效应的模拟[49]。张晓青等采用D2Q9热格子气模型,研究了热声热机中的驻波传播运动,发现了非线性的涡流耗散,验证了格子气的模拟效果[50]。Rahman等基于人工神经网络(ANN),预测某一热声换热器在某些工况下振荡传热系数,其预测结果与实验结果较为一致[51]。Peng等使用遗传算法优化驻波热声制冷机中的热声板叠,其结果与DeltaEC建模的比较表明,该方法在预测声场和能量流方面是有效的,并且根据模型得到最优的板叠间距、孔隙率、频率以及代表COP值的冷却功率的Pareto前沿值[52]。 微电路中的热量堆积对其性能有很大影响,当前的制冷机大且笨重,热声制冷机可以有效克服上述缺点。美国犹他州的声学中心对热声机械与电子电路集成进行研究,提出如图5(a)所示构想,并且对其进行了理论上的论证。在常压下,较低的能流密度会严重影响热声制冷机的效率,Direk与Petrina对微型化的热声制冷机进行研究,设计了一套充压的谐振系统,目的是提高能流密度,在冷端与热端之间产生12.4 ℃的温差[53-54]。Symko等使用热声机械对微电路中的热量进行管理与冷却,开发出了2种解决微电路热量的新方法:①热声制冷机通过声波(高频谐振)产生温度梯度,对微电路制冷(图5(a));②热声原动机将热量直接转化为声能,从而消耗热能(图5(b))[9-10]。 图5 犹他州立大学的微型热声制冷机构想图Fig.5 Micro-thermoacoustic refrigeration mechanism at Utah State University 第一台热声制冷机是Holfer研制的(图7(a)),利用扬声器驱动装置制冷,谐振管为能抑制谐波与降低损耗的球型容器,氦气及其混合气体为工质,工作压力为1.0 MPa,当输入谐振管的声功为10 W,在冷区将获得了193 K的最低制冷温度[55]。胡鹏等研制了用于微型制冷的PZT声驱动器(压电驱动器),与谐振管相匹配,可以得到高振幅的声压,在均压2.1 MPa空管实验时,声压峰值最高可达0.3 MPa,在样机上实验时,冷端与热端的温差以及热端温降达到31和15.2 ℃[56]。 Garrett等将热声装置应用于太空领域,建造了一台1/4波长的空间热声制冷机,在400 Hz的工作频率下,制冷温差为80 K时,得到3 W的冷量[57]。之后,Balliste又建立了1/2波长的冷却舰载雷达电子元件的热声制冷机,在320 Hz工作频率条件下,制冷温度为297 K,得到205 W的冷量[58]。余国瑶等研制了液氮温区的300 Hz高频驻波热声发动机驱动单机脉管制冷机,在发动机加热功率为500 W,均压4.0 MPa下获得了67.5 K的最低制冷温度[59]。 罗二仓的团队建立了一种双作用式液体活塞的行波热声发动机,可以显著的提高热声发动机的效率,在均压1.5 MPa,加热功率为1 500 W时,得到1.45的压比,实验装置如图6所示[60]。 图6 双作用液体活塞的行波热声发动机Fig.6 Double-acting traveling-wave thermoacoustic heat engine using liquid pistons 图7 制冷机示意图Fig.7 Schematic of the refrigerator Swift与Radebaugh将热声驱动器代替机械压缩机驱动小孔脉管制冷机(图7(b)),研制成功世界上第一台无运动部件的制冷机,在最佳条件下能产生90 K的制冷温度[61]。之后Los Alamos国家实验室、国家标准技术研究所以及Cryenco公司成功地研制了燃气驱动脉管制冷机,该制冷机是当前唯一的实用化热声制冷机[62]。到目前为止,该工程第三期针对20 000 gpd液化率的发动机驱动脉管制冷机进行研究,预期实现以15%的天然气燃烧作为动力,液化剩余85%的天然气[63]。 胡剑英等设计了一种用于液化天然气的高效1 kW级行波热声制冷机。加热温度923K,加压氦气7 MPa,可获得1.17 kW的冷却功率和14.95%的总火用效率,对加热温度和平均压力对系统性能的影响进行了仿真,结果表明,在110K时,系统总(火用)效率为14.95%,冷却能力为1 170 W[64]. 金滔等提出了一台发动机和一台制冷机结合的环形行波热声制冷机,重点研究了发动机和制冷机的归一化声阻抗、体积速率和再生器中行波相关的相位关系[65]。 Sharify等构建了由多级行波发动机驱动的双环型行波热声制冷机,当发动机板叠热端温度TH超过85 ℃时发生气体振荡,当TH达到90 ℃时,观察到制冷(-42.3 ℃),TH=270 ℃时,可以达到-107.4 ℃的最低温度,当整个系统为-50 ℃时,测得的最大COP为0.029[66]。 在太阳能发电方面,热声装置可以单台小功率运行,也可以多台联合实现大功率运行,是太阳能光热发电的重要研究对象。Chen等建立了第一台太阳能驱动的1/4波长热声发动机原型,使用菲涅尔透镜将太阳能聚集,同时使用电辅助,在开口端1 m处产生120 dB的音量,之后建立的太阳能热声发动机驱动制冷机由于气体泄漏与热损失等原因,只能达到1.8 K的降温效果[67]。Backhaus等建立了一个行波热声发电机的实验台,可以得到24%的热声转化效率,声电转化效率为75%,最终的热电转化效率18%[68]。戴巍等在热声脉管制冷机中加入起耦合作用的声学放大器,在热声发动机驱动的二级脉管制冷机中得到18.3 K的温度[69]。吴张华等建立了千瓦级太阳能热声发电示范工程,在加热器750 ℃时可以获得200 W的电能[70],如图8所示。之后,吴张华又采用直线电机研制出了双作用型的行波热声发电系统,热端换热器的温度为650 ℃,热电效率为16.8%,得到了1.57 kW的电能[71]。 Bi等建立了多级行波热声发动机和线性交流发电机组成的新型行波热声发电机,实验中,氦气加压为6 MPa,加热温度与冷却温度分别为650和25 ℃时,最大电功率为4.69 kW,热电效率为15.6%,最大电功率为3.46 kW时,最大热电效率为18.4%[72].最近,吴张华建立了一个能够利用LNG(液化天然气)冷能的双作用热声斯特林热电发电机,该系统由4个单元的热声斯特林发动机和4个端对端连接的线性交流发电机组成,构成一个环路配置,发动机通过完成LNG提供的低温与周围环境的低温之间的热声斯特林循环,将外部热能转换为声功。当电阻和电容分别为160 Ω和80 μF、冷却和加热温度分别为110 K和303 K,孔隙率为0.9,水力半径为53 μm时,整个系统的最大声功17.6 kW,最大的电能为12.4 kW[73]. 胡剑英等设计一种新型热声斯特林发动机,由压缩机,再生组件,置换器和交流发电机组成,通过数值模拟得到当加热温度为900 K时,该系统的总效率可达47%[74].金滔等建立了由三级环形热声发动机和线性交流发电机组成的三级环形热声发电机,调节外部电阻和频率来调节线性交流发电机的声阻抗,采用He-Ar混合物调节频率,在 He-Ar混合物作为工作流体的 120 ℃的高温下,可以实现1.51%的最大热电效率,其中氦的摩尔分数为0.63[75]. 图8 太阳能行波热声发电装置Fig.8 Solar-powered traveling-wave thermoacoustic electricity generator system 一般的工业生产会产生大量的低温余热,由于热声发动机的起振温度较低,可以对大部分低温余热进行回收再利用。Mumith等利用DeltaEC软件设计了能够利用食品制造产生的低温余热的热声发动机,理论计算得到在相对较低的温度下(150 ℃以下),热回收产生了1 029.10 W的声功率,热机的效率为5.42%[76].若要实现生产过程中低温余热的有效利用,降低发动机的热端起振温度格外重要。Tsuda等为了提高热声发动机的效率,分别研究不同的含水量以及板叠特征长度对热声振荡的临界温度影响,实验显示了当水量超过一定值时,临界温度突然降低,当加入水时,板叠特征长度对临界温度的影响变小[77]。之后,又研究了不同含水量下,热声发动机的临界温度特性,发现当含水量增加一定值时,临界温度可降低近100 K[78].Saechan等利用日常烹饪过程中生物燃料燃烧中产生的废热作为驱动热源,将热声发动机与热声制冷机联用,用来冷藏处理重要的药物,实验得到冷却器的最佳位置,并在+8 ℃的储存条件下,可实现-8.3 ℃的最低温度和高达7 W的冷却功率[79]。陈国邦与金滔等研制了长为4 m的双端驻波热声发动机,在实验过程中发现了“滞后回路”现象,并以氮气为工质,在2 000 W的加热功率和2.58 MPa的充气压力下,实验得到了1.123的压比[80]。汪双凤等人设计了一台利用低温余热的热声样机,研究发现在合适的板叠结构和材料下,该样机的最低高温侧起振温度(热端冷端温度差)可达到60 ℃[81]. 随着热声理论的发展,热声机械应用于各个行业,建筑火灾发生时,由于火焰向上蔓延,在顶棚形成高温烟气层,这样的高温可以激发热声装置发出报警声信号,实现无源报警。因此,热声轰燃报警器是火灾报警器的最新发展方向之一。 图9 马里兰大学热声轰燃探测器装置Fig.9 Thermoacoustic flashover detector of university of maryland 为了防止轰燃对消防人员的危害,马里兰大学的Buda-Ortins开发了一种基于热声转换的消防员头戴式轰燃探测器原型,其结构为1/4波长驻波的热声发动机,在44 W与31 W的热输入功率下对热声发动机的温度与声音特性进行分析,在装置开口端测试得到115 dB(500 Hz)的声音,装置开口端位于消防员头部38 mm时,有较为理想的报警效果,其装置原型如图9(a)[11]所示。为了使装置更加简单,Hamburger对Buda-Ortins装置进行了优化,去掉了冷端换热器,重新设定了装置的几何参数,可能是由于装置气密性不良的因素,最终没有发出声音,但实验过程中发现加水会降低原型机发声温度,为了更好收集热量,在其原型装置的基础上增加了热管与热收集板(图9(b))[12]。Jeffrey对Hamburger与Buda-Ortins的实验进行了总结,并测试了不同板叠充填材料对装置发声温度的影响。为了保证测试热管和热收集器的实际效果,实验时Jeffrey将整个热声轰燃探测器原型安置在热辐射面板前,当热流密度为25 kW/m2,热端换热器达到125 ℃(7 min后)时,原型机发出声音(图9(c))[13]。 热声装置维护成本低,有较为小巧紧凑的几何结构,是出色的消防警报装置,由于装置的装配以及换热问题,马里兰大学对热声装置的应用研究只停在初始阶段,如果能设计出良好的可应用于消防方面的热声报警装置,将对保证人民财产安全有着非常重大的意义。 从发现热声效应到目前为止,国内外学者从不同角度对其开展了大量的研究,在理论及工程应用方面取得了很大进步。由于无源、环保、变害为利等优点,热声装置在很多方面都显示出了其独特的优越性及广阔的应用前景。根据以上的研究状况,为了能够深化理论与推广应用,提出一些亟待解决的问题。 1)线性热声理论得到很大的发展,但是线性理论只适用于小振幅热声效应,未来的热声应用如热声发动机将会集中于大振幅方面,所以能够解决大振幅的理论研究是需要突破的重点之一; 2)应用先进的物理化学测试仪器能捕捉到宝贵的实验现象及结果,此外,数值模型也可以定量的计算出热声效应中各状态量的动态变化,两者相互印证、相互补充、能够更加深刻的理解热声效应,是解决非线性热声效应的强有力手段; 3)由于小型热声制冷机中声功率密度较低以及能量易耗散的原因,相应的工业性研究仍然难以开展,因而仍局限于实验实验室研究。对电子原件进行冷却的高频微型热声装置已有较为成熟的理论构想,急需开展微型样机的研发工作及小型热声制冷机的工业性实验; 4)热声装置结合其它结构,例如制冷脉管、压电设备、声学放大器等可以有效地拓宽热声效应的应用范围,提高热声机械的应用效率。依托热声转化的独特优势,在热声理论的指导下,合理设计优化热声机械,实现其与其它结构的有效衔接,热声效应将在航空航天、清洁能源、电子散热、消防等行业大放异彩。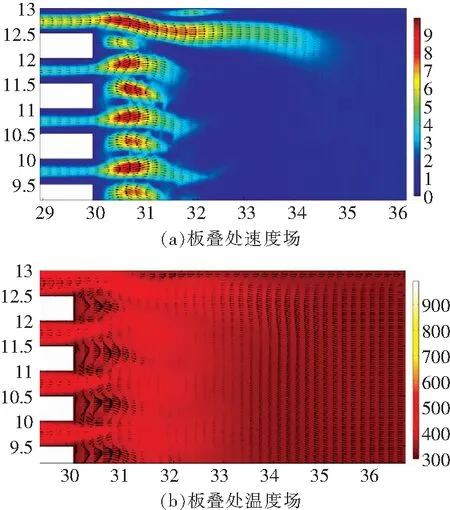
2 热声效应研究方法
2.1 实验研究

2.2 数值模型
3 热声效应的应用
3.1 热声制冷机
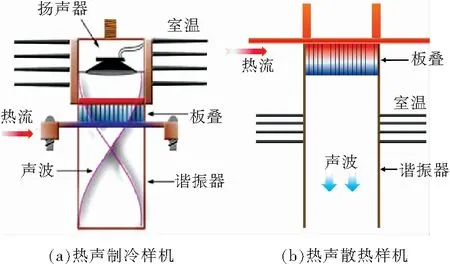

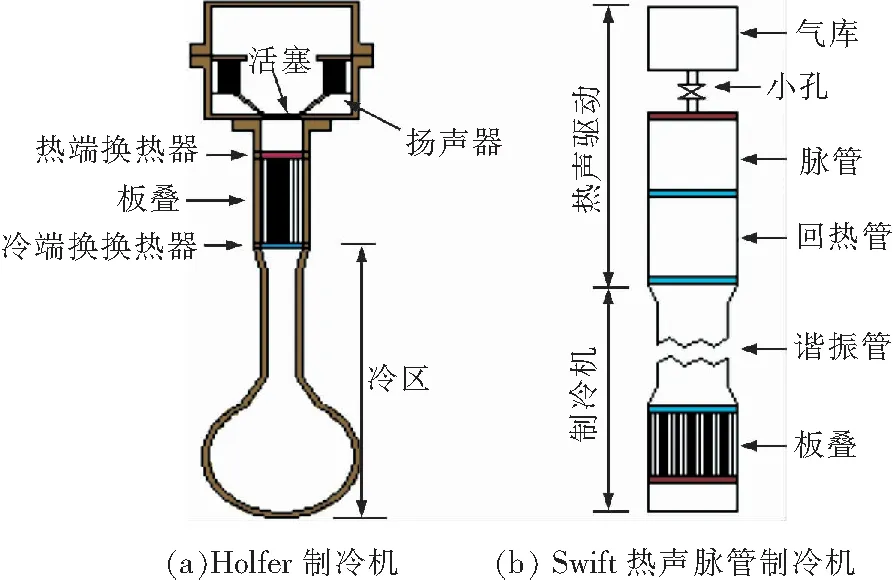
3.2 热声发动机

3.3 热声轰燃探测器

4 结 论

