低风速区风机偏航控制策略研究

陈志昊，朱兆强，余豪，张大斌

（1.贵州大学机械工程学院，贵州 贵阳 550000；2.中国电建集团贵州工程有限公司，贵州 贵阳 550000）

1 前言

偏航系统作为水平轴风机的重要部分，主要承担着将风机叶轮面转向风来向，使风能正对通过叶轮。传统风机偏航控制系统主要通过获得当前风向信息并快速发出偏航指令，这一方式在高风速区风场中能满足一定的控制要求。但风机偏航动作不是瞬时完成的，转动越大的角度所用的时间也越长。低风速区风向相较于高风速区变化较为频繁，若仍使用传统偏航控制系统，风机可能出现随变化的风向不断偏航，无法稳定运行。

为了解决上述问题，同时对风机更好的进行控制，基于风况预测下的风机控制系统研究开始出现。文献[1−2]均使用改进的BP神经网络对风向进行预测，并用以指导偏航动作，但仅研究了短期预测对偏航的指导情况，且使用的风况数据变化较小，不适用于低风速条件；文献[3]针对风向变化较大的山地风电场，研究基于数据采集与监视控制系统的风向预测，并根据采集数据设定偏航策略参数，结果表现良好，但数据处理量较大，实际利用效果未知。提出一种风机偏航控制策略，与传统偏航控制策略进行对比，并针对策略中三个参数进行正交试验分析。

2 风机模型

单位时间内平均流速为v的风产生的动能为：

式中：ρ—空气密度；S—风流过的截面面积。当风正对风机叶轮流过时，S即为叶轮的扫风面积。设叶轮的半径为R，则风机在叶轮正对风向时获得的最大机械功率[4]为：

其中，Cp—叶轮的风能捕获系数[5]，可以由以下式子得出：

式中：λ—叶轮的叶尖速比；β—风机叶片的桨距角；n—叶轮转速，r/min；R—叶轮的半径，m。

从上述公式可知，叶轮正对风向时风机获得的最大机械功率主要受Cp和v影响。考虑到处于低风速区的风机因风速较低，在大部分时间需将桨叶一直处于最大状态，故取叶片桨距角为0°。同时，为简化计算，在风机偏航过程中设定叶轮转速稳定。则上式可以简化为：

当风机叶轮不正对风向时，风机仍可获得一定的风能。设叶轮法线与风向夹角为α，当α<90°时，风仍可视为从叶轮正面通过，此时风通过面积等效为椭圆。

则叶轮法线与风向夹角为α时，风通过叶轮等效椭圆面积为πR2cosα。即一般条件下风机叶轮获得的机械功率Pα=Pcosα。因此，当风机处于为正对状态，如正在偏航动作时，仍会获得较少的风能。

3 偏航控制器设计

偏航控制策略主要可分为判断与动作两个部分。先判断风机的下一次偏航是否为较大浪费，再根据判断结果选择进行顺序判断或是直接执行偏航动作。

3.1 控制策略原理

每秒风况数据过于庞大，且会造成风机动作过于频繁，一般将一个时间段作为一节，每节的平均风速和盛行风向代表本节整体的情况。在进行风况预测时，需要预测当前小节p之后N个小节p+N的数据，则N为预测间隔。不同小节时间与预测间隔在时间轴上对应，如图1所示。

图1 小节时间与预测间隔Fig.1 Bar Time and Prediction Interval

如图2所示，当确定了预测间隔N，从当前小节p到预测小节p+N之间的所有小节都已由p之前的小节预测完成，即当前已获得p，p+1，…，p+N小节的预测数据。用这几节数据便可对风机控制做出指导。

低风速区风向变化频繁，一般设定一个误差范围，若叶轮法线与风向夹角在此范围内，则认定风机已经与风向处于正对状态。如图2所示，叶轮法线与风向夹角为7.5°内均认定为正对状态，则风向两边包含的区域总共为15°[6]，即将一个圆周分割为360°/15°=24 个扇区。此外还有16 扇区，对应的误差范围为11.25°等。将圆周分割为不同的扇区能保证风机不会应较为精确的风向而频繁地触发偏航动作。

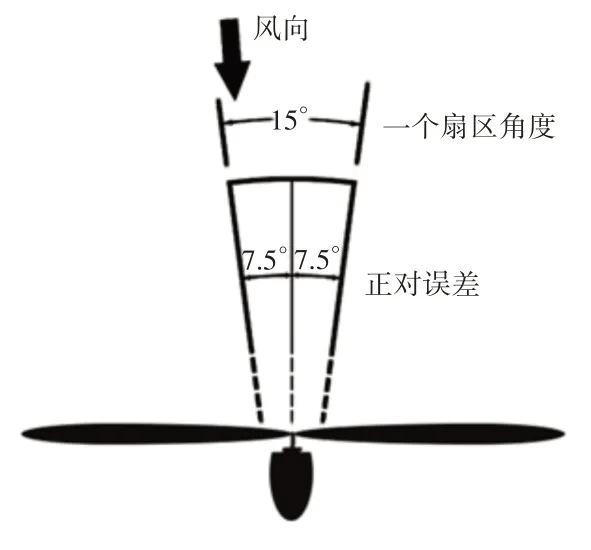
图2 正对误差Fig.2 Positive Error

大型风机叶轮较大，为防止产生较大的振动，偏航动作不宜过快，一般取小于1°/s[7]。具体偏航转动速度由风机结构决定，根据情况参考风机厂商设定的额定偏航速度。

当前期进行风况预测时，考虑到不同的预测算法，使用不同的参数，完成每次预测，都可能产生不同的预测结果。即预测存在一定的错误率，每次不同的错误数据输入控制策略中都可能影响最终风机所获机械能的情况。

因此为了减小预测算法对控制策略的影响，对原始风况数据进行随机处理，模拟风况预测的过程。设定预测算法具有80%的正确率，则在预测完的风况数据中有20%的数据发生错误，即随机对20%原始风况数据进行修改，模拟算法对风况数据的预测。

3.2 偏航控制策略

设当前小节为p，预测未来第N个小节风况数据，即预测小节为p+N。当控制策略运行时，从当前小节到预测小节的未来风况数据均由历史数据预测出，即小节p，p+1，…，p+N的风况数据均已预测出。风机在正常情况下的偏航目标小节为p+1 小节。若从当前位置偏航至p+1小节所用时间大于一个小节时间，则p+1小节风机都一直在进行偏航动作，这将严重浪费小节风能。这时需要由控制策略控制将偏航目标小节调整为p+n小节（n=1，2，…，N）。将从当前位置经过每一小节偏航至p+n小节所用时间大于n个小节时间，作为判据一。

式中：T（a，b）—从a小节偏航至b小节所用时间；t0—单位小节时间。

将从当前位置直接偏航至p+n小节所用时间小于n个小节时间，作为判据二。

当判据一、二均符合时，认定直接偏航至目标小节能减小风能浪费。故风机可以直接偏航至p+n小节。若判据一或二有不符合，则将目标小节向后推进一节。

当目标小节推进至p+N小节，无法再向后推进，则认为这段时间内的风能不得不浪费，因此执行与绕缆方向相反方向的偏航动作，解开一部分因偏航造成的绕缆情况。当风机向目标小节偏航时，偏航动作会占用一部分时间，进而浪费了部分风能。因此需要考虑将偏航动作的时间尽可能分配在较低风能的小节。通过预测目标小节p+n的风速，计算并对比当前小节与目标小节中风机所获机械能。

式中：P—式（4）中风机所获机械能关于风速v的函数；vp—当前小节预测的风速；vp+n—目标小节预测的风速。

若式（7）成立，则不应浪费当前小节的风能，在当前小节结束后执行偏航动作。否则，偏航时间不应占用目标小节，则根据偏航动作所用时间计算偏航开始的时间。

为防止因过度绕缆而损坏风机，当绕缆达到1080°时［8］，应立即停机，并执行解缆动作。本控制策略整体流程图，如图3所示。

图3 基于风况预测的偏航控制策略流程图Fig.3 Flow Chart of Yaw Control Strategy Based on Wind Prediction

4 仿真试验

对上述偏航控制策略使用Python进行仿真研究。风机仿真主要参数为：风机类型为水平轴；风轮半径为37.5m；风机额定转速为17.3m/s；偏航电动机运行速度为0.5°/s；最大偏航角度为1080°。对于每次试验，都使用进行80%正确率的模拟预测后的数据作为输入，计算通过本文控制策略输出风机获得的机械能。

4.1 传统控制对比

为了与传统偏航控制方法进行比较，建立传统偏航控制模型。传统偏航控制在接收到当前风向数据D后，会进行一定时间的等待，以防止风向往复变化或测量错误。在确定风向已经变化后，风机开始朝着当前风向进行偏航动作。具体流程图，如图4所示。为了便于进行对比，传统偏航控制模型[9]的输出也设定为风机获得的机械能，并使用相同的原始风况数据作为输入。使用原始数据分别进行13次80%正确率的模拟预测，计算在不同参数的控制策略下风机获得的机械能。并使用相同原始数据，计算在传统控制策略下风机获得的机械能。传统控制策略没有预测过程，多次试验并无差异，故仅做一次试验。两种结果，如图5所示。

图4 传统偏航控制策略流程图Fig.4 Flow Chart of Traditional Yaw Control Strategy

图5 不同参数的控制策略与传统控制对比Fig.5 Comparison of this Control Strategy in Different Parameters and Traditional Control

可以看出，使用本控制策略在不同参数、不同预测情况下，风机所获的机械能都高于传统控制策略。

4.2 正交试验

控制策略中存在小节时间、预测间隔、扇区分割三个可变参数，若进行全面试验较为繁杂。正交试验对参数进行组合，能极大简化试验数据[10]。根据计算程度与实际影响，选取小节时间8组，选取扇区分割和预测间隔分别4组，建立三因素混合水平正交试验，正交试验参数，如表1所示。

使用Python对正交试验表中组合进行试验，每组参数都进行13次80%正确率的随机模拟预测，记录每组试验风机分别获得的机械能。

5 结果分析

5.1 显著性分析

为确定试验结果的差异性是由于因素水平的改变，而非其他因素或试验误差导致，需要先对试验结果进行显著性分析。方差分析可以检验不同参数对结果的显著性影响。使用SPSS软件对试验结果进行F统计值显著性检验。

依据F分布表，若P<0.05，则表示变量对指标影响显著。在风机所获机械能指标下，三个变量的显著性值都小于0.05，说明扇区分割数、小节时间和预测间隔都对风机所获机械能具有显著性影响，如表2所示。

表2 不同参数方差分析Tab.2 Variance Analysis of Each Parameters

5.2 极差分析

极差分析能得出不同因素对指标的影响程度结果，如表3所示。

表3 极差分析Tab.3 Range Analysis

从表3中可以看出，对风机所获机械能影响最大的是小节时间，其次为预测间隔和扇区分割。

从图6可以看出，小节时间的最优水平为120s，且风机所获得的机械能随小节时间变长而上升，但上升趋势逐渐变缓。这主要是由于低风速数据变化频繁，若取较长时间作为一小节时，则使用平均风速和盛行风向代表整个小节风况，能进行更少的偏航动作，而不用因频繁进行偏航导致浪费风能。扇区分割的最优水平为20扇区，随分割增多，指标也随之上升。扇区分割越多，风向越精确，越能保证较小的正对误差。预测间隔的最优水平为5小节，且指标随预测间隔增大有大幅度上升，但到6小节时还有小幅下降。这主要是由于预测间隔过大后，风机会因多种控制策略做出跨过多小节的偏航动作，浪费了一定风能。且可能出现由于预测错误，导致的预测间隔偏航动作混乱，进而浪费了整个预测间隔内的风能。

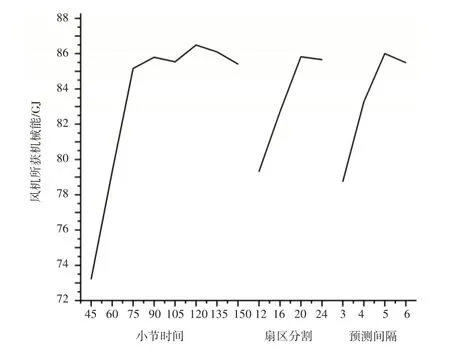
图6 三因素指标图Fig.6 Three−Factor Indicator Chart

因此，根据正交试验所得结果，选出最优组合为A6B3C3，即取小节时间为120s、扇区分割为20扇区、预测间隔为5小节时，使用本文控制策略能使风机具有最佳的获能。

此外，扇区分割数对于输出的影响不是非常明显。从表3可以看出将一个圆周分成数量更多的扇区，风机获得的机械能更多，但差距较小。扇区分割越多，风向越精确，越能保证较小的正对误差。但扇区分割过多会导致计算量变大，还应根据实际情况选择合理的扇区分割数。

6 结论

提出一种控制策略，并将其与传统偏航控制方法比较，结果表明本策略能更好适应低风速下风况变化频繁的问题。同时，对风机偏航控制策略三个参数进行正交试验，分析结果表明：小节时间、扇区分割和预测间隔都对风机所获机械能具有显著性影响，其中小节时间影响最大，扇区分割和预测间隔具有一定影响。