永磁同步电机干扰观测复合滑模控制技术*
程 勇, 李思卿, 李森豪
(西安科技大学 电气与控制工程学院,陕西 西安 710600)
0 引 言
随着电力电子技术的发展和材料技术的进步,永磁同步电机(PMSM)的制作工艺和控制性能均得到了提高,其展现出了高功率密度、高工作效率、结构简单等优点,在轨道交通、工厂机床、航空领域应用广泛[1-3],因此其控制方法也成为了学者们研究的热点。
在PMSM的控制方法中,一般要求控制方法可以使控制系统有较快的响应速度,较强的干扰抑制能力,在参数失配后可以维持控制性能的鲁棒性。为了达到相应的控制要求,多种针对PMSM的控制方法应运而生,目前使用较为广泛的就是PI控制。其控制结构简单,不依赖于控制系统的模型,因此对电机参数失配可以表现出较好的鲁棒性。但在面对控制性能要求较高的场合时,PI控制很难呈现出相应的控制性能,在面对非线性系统时,不能调整自身的特性来应对复杂的控制对象[4]。因此,学者们不断深入研究,提出了内模控制、滑模控制(SMC)、自适应控制和智能控制等控制方法。其中SMC结构简单、鲁棒性强[5],在实践中已经获得了广泛的应用。SMC是一种非线性的变结构控制,在多数文献中均已应用于电机的控制性能改善。在文献[6]中,提出使用滑模观测器(SMO)来观测误差,并以此对SMC和PI控制器进行实时的权重分配,同时根据SMO设计了转角速度补偿器对误差进行补偿,提高了转速环的控制性能。但是在SMC的过程中,由于滑模自身的结构特点,通常会产生一定程度的抖振现象。在文献[7]中提出了一种新型混合趋近律,并结合积分型滑模面,提高了控制系统的干扰抑制能力,有效地降低了抖振。在文献[8]中使用模糊控制建立规则动态的调节SMC的收敛速度,同时使用连续函数代替传统SMC中的开关函数,有效改善了SMC的抖振。
然而,在传统线性滑模面分析中,发现线性滑模面控制不能使状态变量在有限时间内收敛到0。针对此问题,在文献[9]中提出了一种非奇异终端滑模控制(NTSMC)来代替传统的PI控制,有效提高了控制精度,降低了超调。在文献[10]中引入了扩张状态观测器来观测扰动,对NTSMC进行前馈补偿,增强了系统的抗干扰能力。然而,在对于NTSMC的进一步研究中发现系统状态远离平衡点时收敛速度慢。针对此问题,文献[11]中提出将线性滑模面与非线性滑模面进行组合应用,结合线性滑模面在远离平衡点收敛速度快的优点,提高了SMC在全局过程中的收敛性。同时,设计了扰动观测器,降低对滑模高增益的依赖性。
在本文中,设计了一种新型的基于线性和非线性组合的积分型滑模面,解决NTSMC系统状态远离平衡点时收敛速度不佳的问题。其次为了提高SMC在全局阶段的趋近速率,在传统的幂次趋近律中设计了以滑模面为自变量的可变因子,改善传统幂次趋近律,以适应在不同阶段的控制要求。最后,本文使用了积分型滑模面的SMO来观测控制系统中的未知干扰,减小观测器的稳态误差,再将观测值补偿到控制器中,降低因滑模高增益所带来的抖振。本文通过仿真和试验证明所提出的SMC方法具有更好的全局收敛性。
1 PMSM及其数学模型
PMSM根据转子上永磁体摆放位置的不同可以分为表贴式PMSM和内置式PMSM,对于表贴式PMSM而言,永磁体紧贴在转子的外表面,气隙均匀[12],气隙的磁密波形更加趋近于正弦波,电机的运行性能更高。
为了对电机进行更加有效的分析,将电机的数学模型建立在dq轴下,同时对电机做出理想化处理,不计涡流和磁滞损耗,假设转子上无阻尼绕组,忽略定子铁心饱和,假设永磁体产生的磁场和三相绕组产生的感应磁场呈正弦分布。得到的PMSM电压模型如下:

(1)
式中:ud、uq分别为dq轴的电压;id、iq为dq轴的电流;Rs为定子电阻;ωe为转子电角速度;ψd、ψq为dq轴的定子磁链。
定子磁链方程为
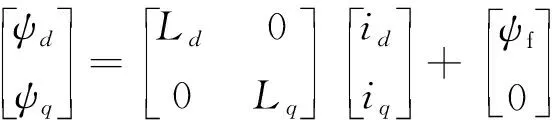
(2)
式中:Ld、Lq为dq轴电感;ψf为永磁体磁链。
电磁转矩方程为

(3)
式中:pn为极对数。
对于表贴式PMSM来说,dq轴的电感是相等的。所以式(3)可以简化为
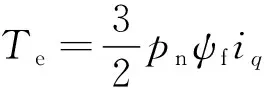
(4)
电机转速环的参考模型为

(5)
式中:J为转动惯量;Te为电磁转矩;TL为负载转矩;ωm为转子角速度;B为摩擦系数。
2 SMC设计
2.1 滑模收敛性分析
SMC是一种变结构的控制,可以在动态过程中,有目的的进行变化,具有实现简单,响应快,对参数不敏感的优点[13]。图1为状态空间中在切换面上三种点的特性。

图1 滑模面上三种点的特性
图1所示,s=0为切换面,将状态空间分为s>0和s<0两部分。在状态空间中,运动点可以分为穿过切换面的通常点,离开切换面的起始点和趋向于切换面的终止点三种。SMC中,将切换面某一区域内的所有点均变为终止点。则可以迫使靠近这一区域的运动点在该区域运动,此时系统在切换面上的运动就叫做滑模运动。
在SMC中,切换面即为滑模面。传统的线性滑模面如下所示:
s=cx1+x2
(6)
式中:x1、x2为系统状态变量;c为正的常数,其中x2为x1的一阶导数,在系统状态到达滑模面之后,滑模面值为0,综合上述可得:

(7)
对上述微分方程进行求解得到状态变量x1从初始位置x(0)到达零点所用时间ts如下表示:
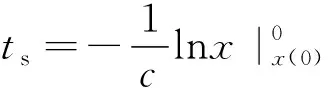
(8)
可知,状态变量无法在有限时间内收敛到0。在NTSMC的设计中,滑模面如下表示:
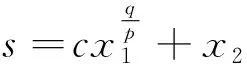
(9)
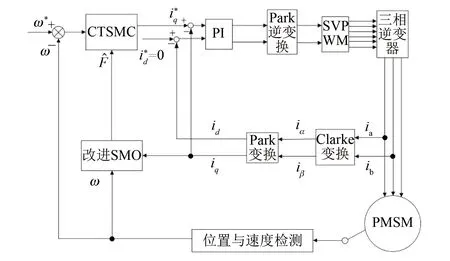
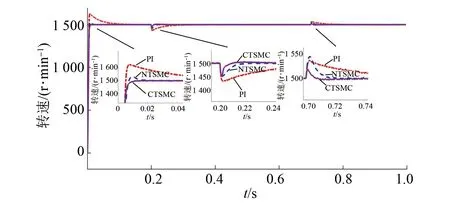
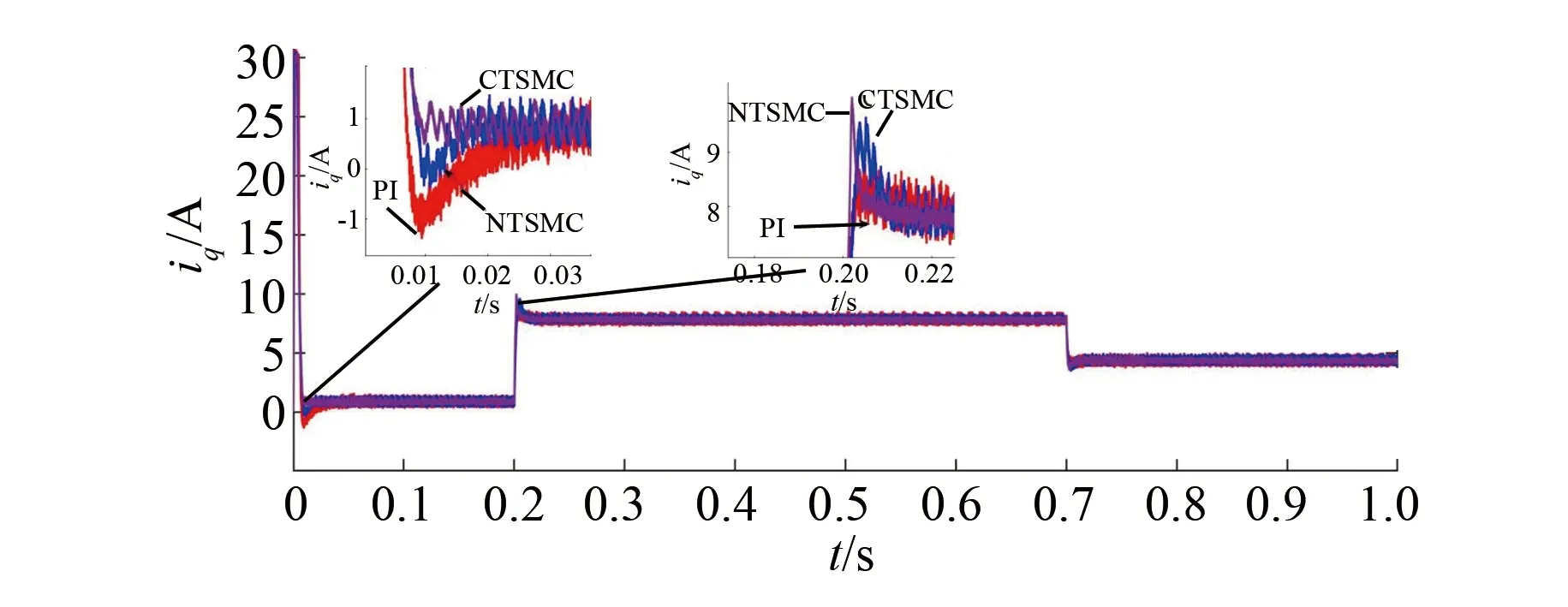
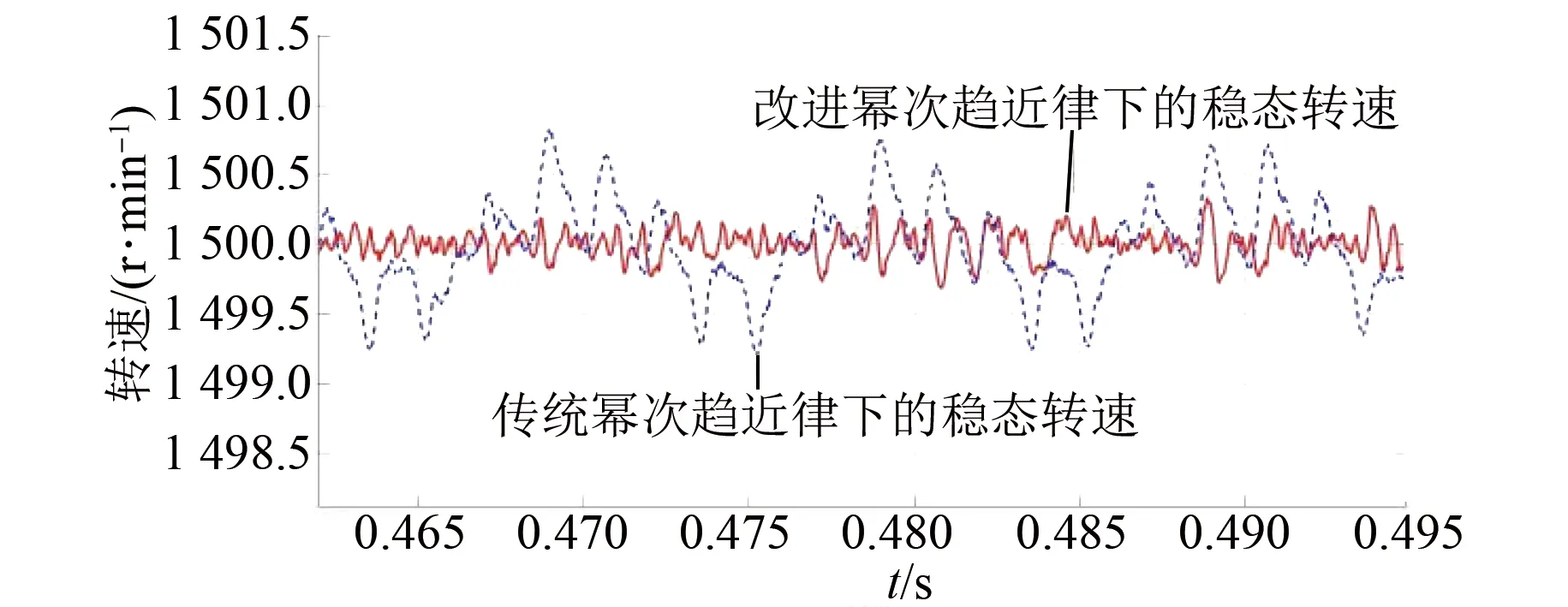
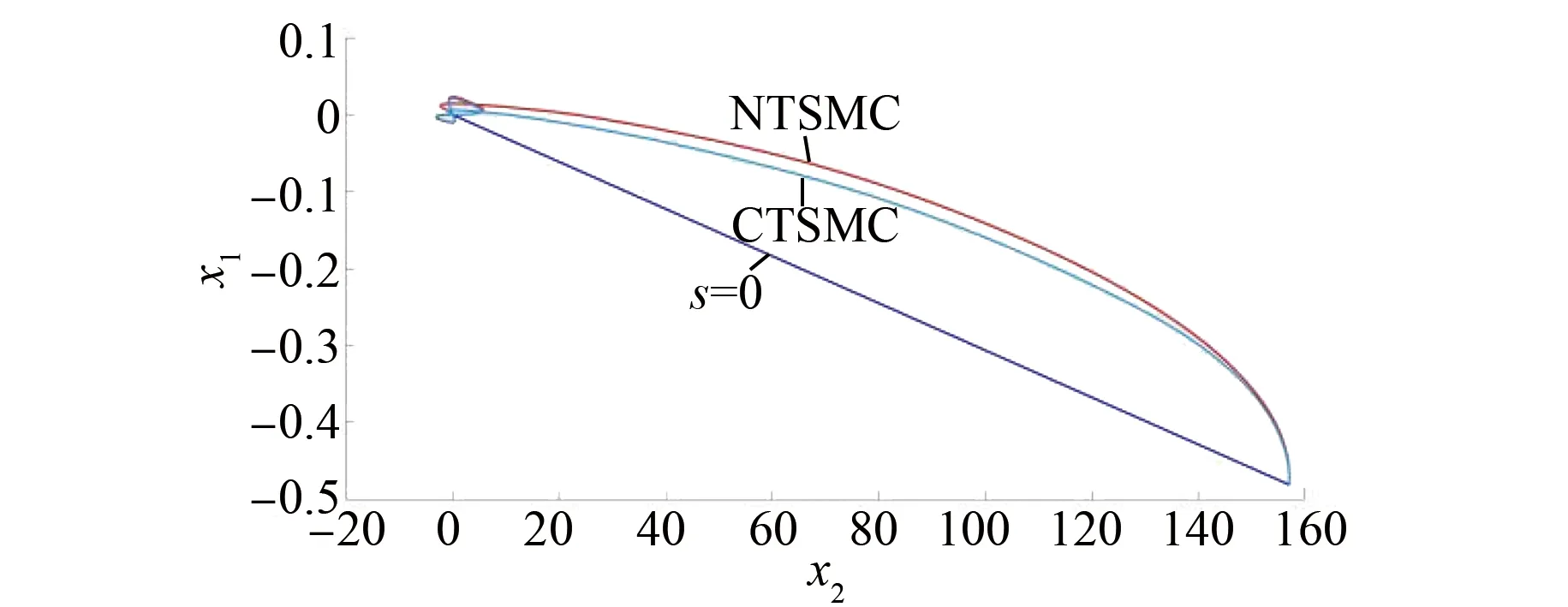
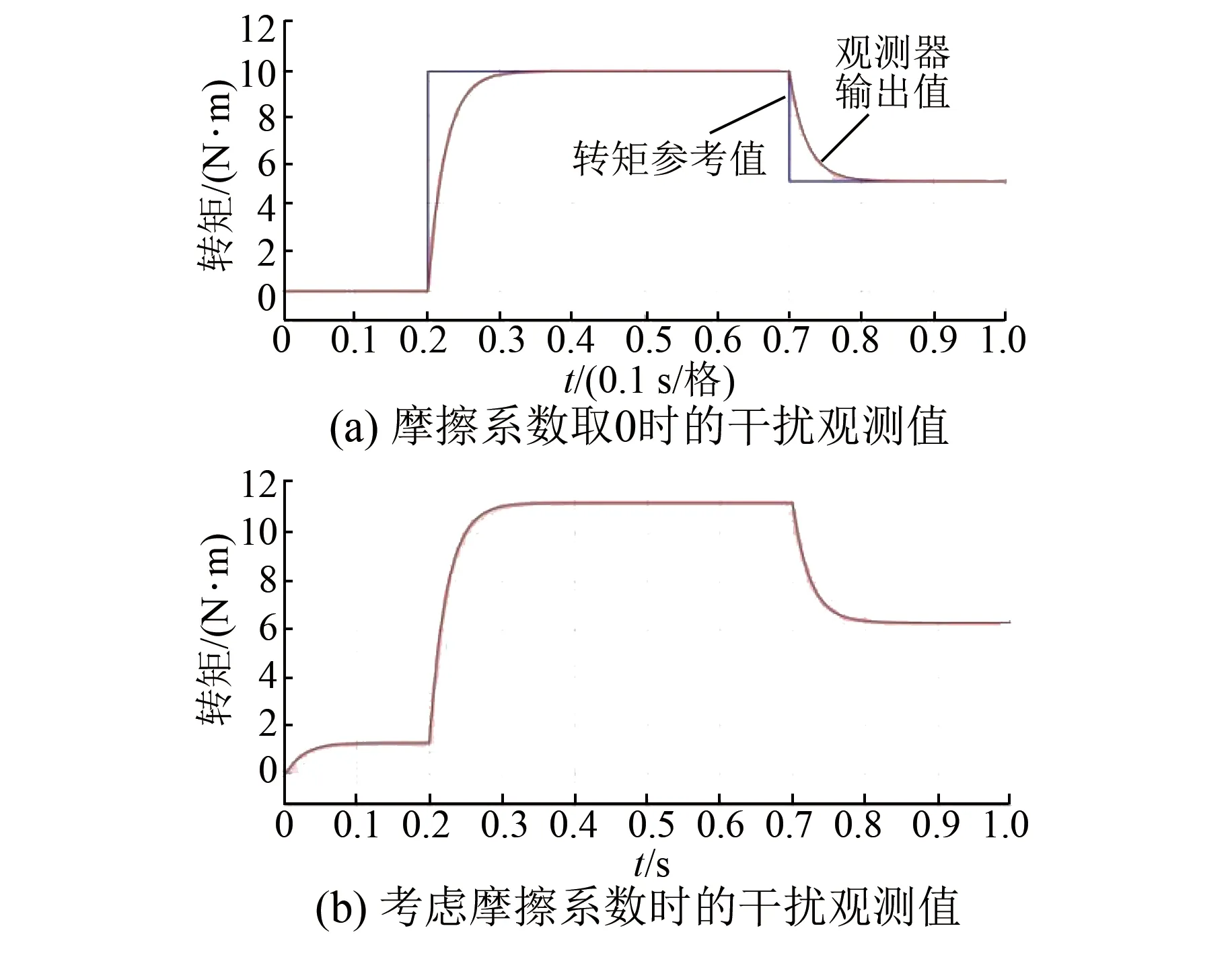
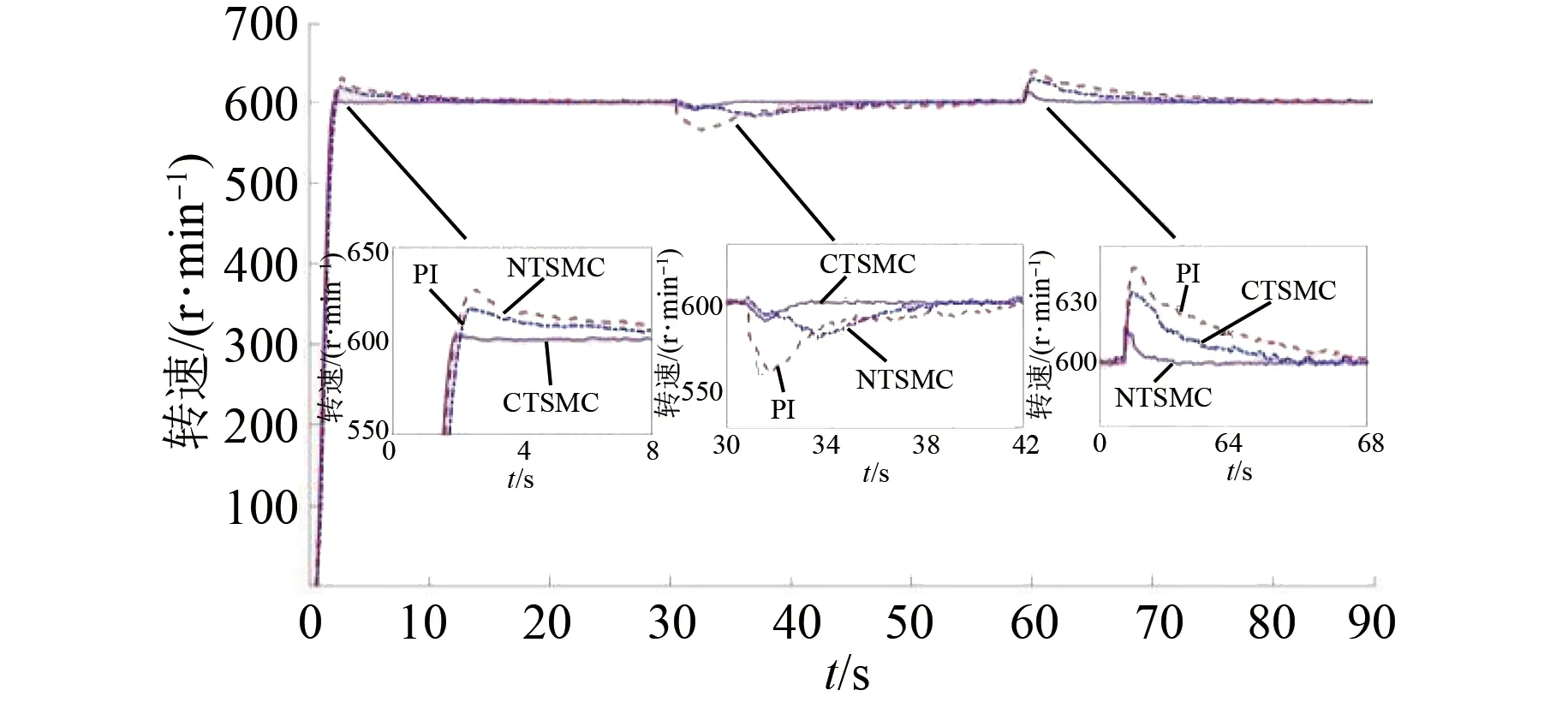
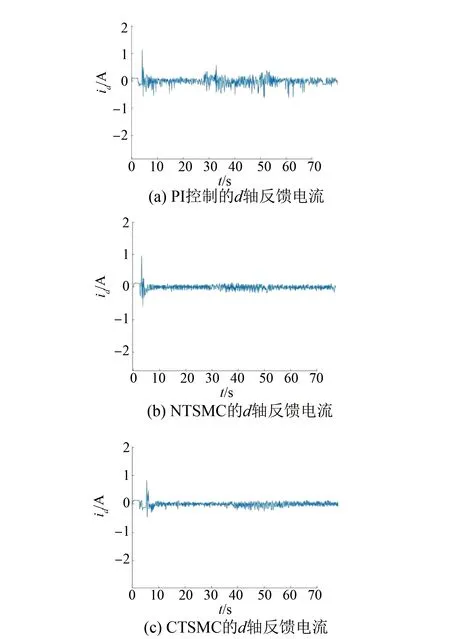
式中:0 有效避免了终端滑模的奇异问题[14],取滑模面的值为0,得到如下微分方程: (10) 对微分方程进行求解,得到NTSMC中状态变量x1从初始位置x(0)到达零点所用时间ts,表示如下: (11) 可知,NTSMC可以使状态变量x1在有限时间内收敛到0。 综上所述,NTSMC可以解决传统线性滑模面构成的滑模控制系统状态变量不能在有限时间内收敛到0的问题,但是NTSMC仍存在有在系统远离平衡点时趋近速率不佳的问题,导致滑模控制反应速度慢。 为了改善NTSMC在远离平衡点位置趋近速度慢的缺点,将线性滑模面和非线性滑模面进行组合,得到如下所示的滑模面: (12) 式中:c1、c2分别为线性滑模面系数和非线性滑模面系数,均为正常数。 将所设计的滑模面代入到电机控制系统中,定义状态变量如下: (13) 将状态变量定义为转速误差的积分与误差,可以更好地减少系统的稳态误差[15],同时定义适当的积分初值可有效降低转速超调。 在定义了状态变量和滑模面之后,对滑模面进行求导: (14) 为了保证状态变量的收敛性,选择趋近律为幂次趋近律,如下所示: (15) 幂次趋近律可以在启动过程中状态变量反馈值较大时,使得SMC收敛速度快。随着状态变量的收敛,收敛速度降低,最终平稳趋向滑模面。 通常来说,在SMC的过程中主要可以分为两个阶段,阶段一是系统状态从初始位置趋近到滑模面的趋近阶段,阶段二是系统状态在滑模面上滑动的滑动阶段[16]。在传统的幂次趋近率中,α为可调系数,当滑模运动处于阶段一时,增大α时,可以提高SMC的反应速度,但是SMC到达阶段二时,滑模面的值在0附近波动,α过大时,反而会降低SMC的趋近速率,因此本文中提出将α定义为以滑模面s为自变量的函数,如下所示: (16) 式中:a为α的上界;b为α的下界,且满足1>a>b>0;h1、h2为自变量的系数。 根据反正切函数和指数函数的性质可知,当自变量s增大时,α的值会逐渐趋近于上界a;当自变量s减小时,α的值会逐渐趋近于下界b。调节参数h1、h2可以调整α对自变量s的敏感性。 将式(13)、式(14)代入式(15)中得: (17) 将式(5)代入式(17)中得控制器如下: (18) 为了证明控制器的稳定型,定义SMC的Lyapunov函数为 (19) 对Lyapunov函数求导得: (20) 将式(17)代入式(20)中得到: (21) 最终根据Lyapunov第二稳定性的定义可知,本文所设计的复合终端滑模控制(CTSMC)策略是渐近稳定的。然而,在实际的电机控制系统中,电机在运行过程中所遭受的负载转矩是未知的,所以为了保证控制系统的抗干扰性往往会增大SMC的增益,但是同时也会使得控制器输出有较大的抖振现象,影响控制系统的精度[17]。 为了解决第2节中提出的问题,本文提出改进型的SMO来补偿受到干扰的控制系统,针对PMSM的转速环建立如下模型,将负载转矩当作未知干扰,摩擦力定义为未建模动态: (22) 式中:F为控制系统所受到的总干扰,包括未知干扰和未建模动态;f(t)定义为控制系统的未建模动态;d(t)定义为系统运行中所受的未知干扰。 为了提高系统的全局收敛性,本文设计了改进型SMO观测系统中的干扰与未建模动态: (23) 将SMO模型与系统模型作差可得: (24) 为了保证观测器的跟随性,定义如下滑模面: (25) 在上述滑模面的设计中采用积分型滑模面,改善观测器稳态误差,可以得到更加准确的干扰观测值。 对滑模面求导得: (26) 取滑模趋近率为幂次趋近率得: (27) ksmo为正的常数,结合式(24)得: (28) (29) usmo=ksmo|ssmo|αsign(ssmo)+c3esmo (30) 由上述可知,以反馈转速和q轴电流为输入的SMO可以成功地观测到系统运行过程中的未知干扰和为建模动态。为了证明观测器的稳定性,同样定义Lyapunov函数如下: (31) 对SMO的Lyapunov函数求导得: (32) 最终得到的基于改进SMO的PMSM NTSMC系统如图2所示。 图2 PMSM控制框图 利用MATLAB/Simulink对本文提出的方法进行仿真,来证明所提出方法的可行性,仿真中所使用的电机参数如下表1所示。 表1 电机参数表 在仿真中转速的参考值为1 500 r/min,在仿真的0.2 s处,突加10 N·m的负载,并在0.7 s处降低负载,变为5 N·m,使用PI控制器、NTSMC和本文提出的基于改进SMO的CTSMC控制器进行对比,来证明所提出方法的优越性。 在CTSMC仿真中,调整滑模面系数c1、c2,在一定区间范围向区域内进行夹逼得到最优值。滑模增益k调整方式与上述相同。值得注意的是可变因子的调整,其中a在取值范围内尽可能取大值,b在取值范围内尽可能取小值。h1、h2应取较大数量级的值,保证α在变化过程中具有快速性和稳定性。 图3为PI控制器,NTSMC与本文所提出的CTSMC转速对比。在电机起动时,PI控制器超调6.6%,并在0.1 s后到达参考转速,NTSMC控制器超调3.6%,在0.02 s后到达参考转速,CTSMC控制器无超调;在达到参考转速后,本文所提出的CTSMC控制器在面对突加和突减负载转矩,可在约0.02 s的时间内恢复到参考转速,NTSMC可在约0.03 s的时间内恢复到参考转速,PI控制则需要约0.08 s。 图3 转速波形对比图 图4和图5为使用PI、NTSMC和CTSMC的dq轴电流对比图,使用本文所提出的CTSMC方法中q轴电流在起始阶段可以以最快的速度到达参考值,并稳定在空载时的参考电流值。且在稳态时CTSMC控制策略q轴电流波动也小于NTSMC和PI控制器,对于d轴电流来说,CTSMC在±0.5 A的范围内波动,而PI和CTSMC波动均超出了±0.5 A。 图4 q轴电流波形对比图 图5 d轴电流波形对比图 图6为使用改进趋近律与传统幂次趋近律控制方法下的稳态转速对比,可以看出在改进趋近律的作用下稳态转速可以稳定在参考值的±0.4 r/min之内波动,较大程度上提高了稳态时的控制性能。 图6 稳态转速对比 最后,图7为CTSMC和NTSMC状态变量收敛对比图,从图7中可知CTSMC比NTSMC在远离平衡点时具有更好的收敛性。 图7 CTSMC和NTSMC状态变量收敛对比图 此外,为了证明本文所设计的SMO可以有效地观察到系统运行中的负载转矩和未建模动态。对观测器的结果进行分情况仿真,如图8所示,图8(a)为取摩擦系数为0时的干扰观测值,此时,仿真中的干扰仅包含负载转矩。起始状态时,所得到干扰观测值为0,在0.2 s处逼近值跟随负载转矩输入值在0.1 s后上升为10 N·m,收敛到准确值,在0.7 s后转矩跟随负载转矩输入值降低为5 N·m,观测结果准确跟随指令值。图8(b)为加入摩擦系数时的转矩观测值,在电机起动时,观测器输出了因摩擦力所产生的干扰,并在加载或者减载以后,观测器输出了负载转矩和摩擦的叠加值。 图8 转矩观测值 为了验证本文所提出SMC和SMO方法的有效性,对上文中所提出的方法搭建试验平台。试验平台主要由电机及电机驱动模块、信号转换模块、信号发送采集模块等部分组成。在电机的试验过程中由张力控制器为试验提供负载转矩,试验所用设备如下图9所示。 图9 PMSM控制系统实物图 图10所示,定义试验中的参考转速为600 r/min,参数调整原理可参考仿真,传统的PI和NTSMC均产生不同程度的超调,PI控制超调5%左右,NTSMC超调3%左右,而本文所提出的CTSMC则不发生超调。在试验的第30 s加入2 N·m的负载,传统PI控制转速下降为参考转速的94%左右,且恢复速度慢,NTSMC转速缓慢下降,下降为参考转速的96.6%,同样恢复速度慢。而本文所提出的基于SMO的CTSMC转速下降为参考转速的98.5%,在5 s左右后可恢复到参考转速,对于突加负载反应速度,抗干扰能力强。在试验的60 s处卸下负载,同样在转速变化和恢复速度上,CTSMC均优于PI和NTSMC。 图10 试验中的转速对比图 图11为基于改进幂次趋近律的CTSMC和使用传统幂次趋近律的NTSMC稳态转速对比图,可以看出本文所提基于改进幂次趋近律的CTSMC在稳态时转速波动在±1.5 rad/min左右,而使用传统幂次趋近律的NTSMC稳态时转速波动在±3 rad/min左右,可有效减小稳态时的转速波动。 图11 试验中的稳态转速对比图 图12为PI、NTSMC和CTSMC的d轴反馈电流对比。 图12 试验中的d轴反馈电流 由图12可知,PI控制起动和加减载的过程中电流会产生较大波动,在约10 s后进入稳态;NTSMC在加载后电流波动增大,在减载后恢复到稳定值;本文所提出的CTSMC在起动时刻尖峰电流最小,在加减载之后的误差也小于PI和NTSMC。 图13为三种控制方法q轴反馈电流的对比图,由图13可知PI控制器在起动,加载减载的过程中均出现了较大的超调和波动,而NTSMC在起动,加减减载的过程中产生了少许尖峰电流,但很快趋于稳定,而本文所提出的CTSMC在起动时刻超调最小,在加减载的过程中反应速度均比PI和NTSMC快,且稳态误差小。 图13 试验中的q轴反馈电流 本文通过分析线性滑模面和非线性滑模面的特点,提出将线性滑模面和非线性滑模面组合,设计了一种新型的复合积分滑模面,并且在基于传统幂次趋近的基础上设计了新型的改进幂次趋近律,使得控制器在运行过程中根据滑模面的值来调整趋近速度,提高控制器的全局收敛性。最后,引入SMO观测系统的未知干扰和未建模动态,对控制器进行前馈补偿,降低滑模控制因高滑模增益而产生的抖振。通过仿真和试验证明CTSMC可以提高滑模控制在全局阶段的收敛性,改善滑模控制的性能。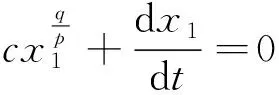

2.2 复合终端滑模控制器设计
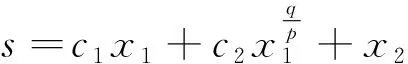
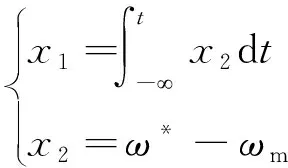
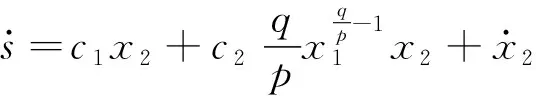
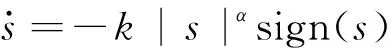


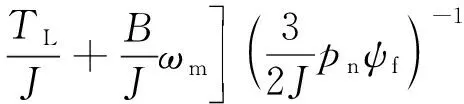
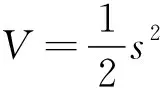
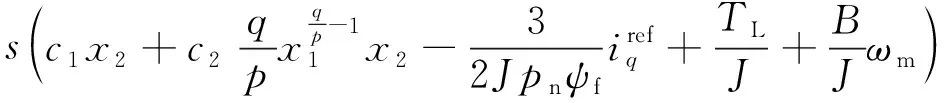

3 SMO设计

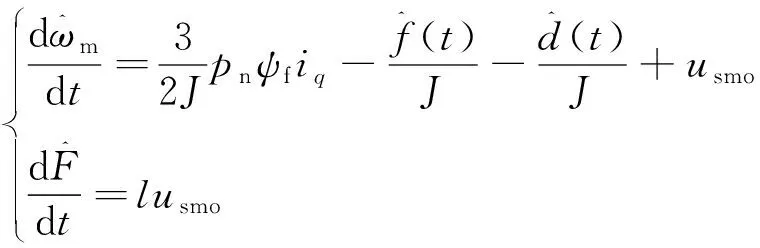

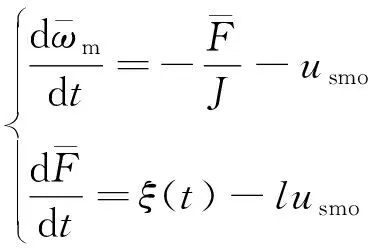
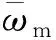

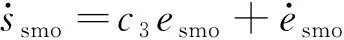
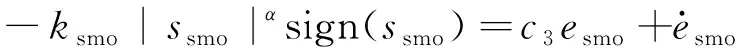
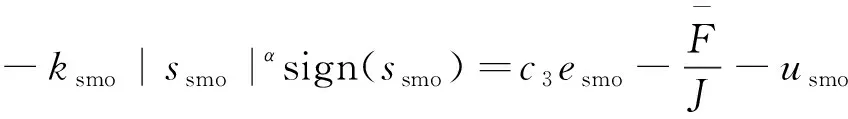
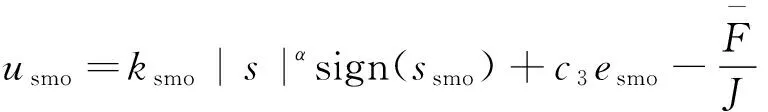
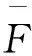
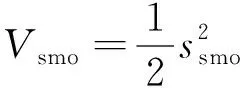

4 仿真分析


5 试验结果



6 结 语

