立体几何中向量方法及其应用

邱和保

(福建省连江第一中学 350500)

立体几何是高考必考的大题之一，而向量法是解决立体几何问题的重要方法之一，《普通高中数学课程标准(2017年版2020年修订)》中提到：运用向量方法解决简单的数学问题和实际问题，感悟向量是研究几何问题的有效工具.运用向量法的关键是空间直角坐标系的建立，不同的建系对运算结果会产生不同程度的影响，因此如何选择建系的方法是解题的关键，从近三年的全国高考卷中可以发现立体几何问题主要考查二面角的正余弦值、二面角的大小以及线面成角，点面距等，具体考点见表1：

表1

从表1中可以发现，以空间几何体作为载体考查空间角的相关问题是高考命题的重点，而二面角的求解则成为高考的热点，对学生来说解决这类问题的关键就是建系方法的选择以及计算，恰当的建系对于简化运算有着良好的促进作用.

1 向量法的使用前提——建立空间直角坐标系

建立空间直角坐标系主要有以下几种类型：

1.1 用共顶点的互相垂直的三条棱建系

例1(2020年北京高考第16题第(2)问)如图1，在正方体ABCD-A1B1C1D1中，E为BB1的中点．求直线AA1与平面AD1E所成角的正弦值．

图1 图2

分析根据题意，要解决问题可以选择用向量法，首先要建立空间直角坐标系，题目所给出的是正方体，根据正方体的几何特征对正方体进行建系，主要是以正方体的其中一个顶点作为坐标系原点，以此顶点为线段端点的棱所在的直线作为x轴，y轴，z轴建立坐标系，从而解决问题.

因此，具体的建系过程如下：

以点A为坐标原点，AD，AB，AA1所在直线分别为x，y，z轴建立如图2所示的空间直角坐标系A-xyz.

1.2 用线面垂直关系建系

例2(2019年全国Ⅰ卷第18题第(2)问)如图3，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．求二面角A-MA1-N的正弦值．

图3

思路2 建系的关键是要在底面中找到两条相互垂直且有交点的线为x轴，y轴，根据题目的条件可知，底面ABCD为棱形，因此AC⊥BD，设其交点为O，只需过点O找到一条与侧棱垂直的直线作为z轴即可完成建系，具体过程如下：

设AC∩BD=O，A1C1∩B1D1=O1，由直四棱柱性质可知：OO1⊥平面ABCD，因为四边形ABCD为菱形，所以AC⊥BD，则以O为原点，可建立如图5所示的空间直角坐标系.

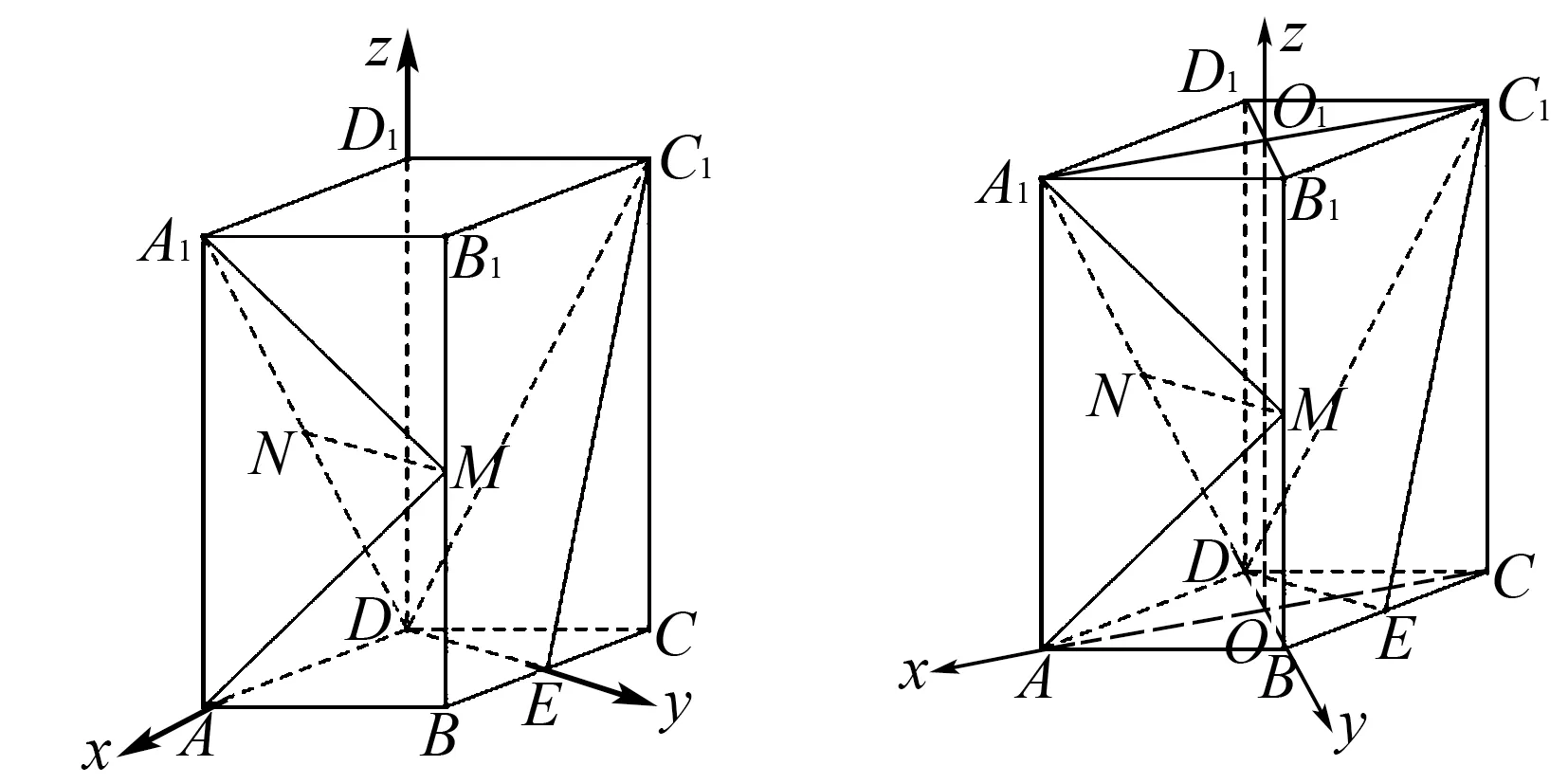
图4 图5

图6 图7

1.3 用面面垂直关系建系

例4(2019年全国Ⅲ卷第19题)图8是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连接DG，如图9所示.

(1)证明：图9中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；

(2)求图9中的二面角B-CG-A的大小.

图8 图9

两种建系方法相比较，明显思路2的方法简化了点E坐标的求法，因此，恰当的建系可以简化点的运算，提高解题效率.

图10 图11

1.4 用正棱锥，圆锥的高所在的直线建系

图12 图13

2 应用——典型例题

例6如图14所示，斜三棱柱ABC-A1B1C1中，平面ABC⊥平面BCC1B1，AB⊥BC,∠B1BC=60°,AB=1，BC=BB1=2.

(1)求A1B与CB1所成角的余弦值；

(2)求A1B与平面ACC1所成角的余弦值；

(3)求二面角B-CC1-A的余弦值.

图14

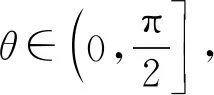
问题(3)的命题角度是考查二面角，因此要联系到二面角的求法：设n1,n2分别是二面角α-l-β的两个半平面α，β的法向量，设θ为二面角α-l-β的平面角，则|cosθ|=|cos〈n1,n2〉|，θ为向量n1,n2的夹角或其补角.

图15

所以△BB1C为等边三角形.

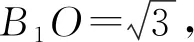
所以设θ为A1B与CB1所成角，则

设n=(a,b,c)为平面ACC1的一个法向量，则

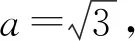
设α为直线A1B与平面ACC1所成角，则

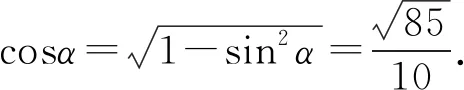
设β为二面角B-CC1-A的平面角，则

3 小结

用空间向量法求解空间角的一般步骤：(1)建系；(2)求相关点坐标；(3)求相关向量坐标；(4)向量运算；(5)得出结论.到目前为止，立体几何中的向量方法仍旧注重几何直观与空间想象的培养，因为建立适当的空间直角坐标系是关键，而这需要空间认识，只不过因向量是自由向量，兼具大小和方向两个要素，可以将抽象的空间位置关系用一个基底加以转化来研究，故而向量方法的教学既有助于培养逻辑思维与数学运算，也有助于培养学生的直观想象核心素养，渗透数学转化与化归思想.为培养学生良好的政治素养、道德品质和科学思想方法起到有效的促进作用.