利用多种思维技巧优化高中数学解题方法

姬成虎

【摘要】高中数学中有很多抽象的概念和复杂的运算，需要学生运用一些特定的思维方法解决问题.有效的思维技巧可以帮助学生更好地理解问题、分析问题，并找到解决问题的方法.文章介绍了五种解题思维技巧：直接法、构造法、换元法、数形结合法和特例法.这些技巧在数学学习中应用广泛，可以使学生更加灵活地运用知识解决问题，培养学生的数学思维和创新能力，提高数学素养和解题能力.

【关键词】思维技巧；高中数学；解题方法

引 言

在高中数学学习中，学生经常会遇到各种各样的难题，例如难以理解的数学概念、难以运用的数学公式、难以推导的数学公式，等等.这些难点常常会导致学生对数学产生抵触情绪，进而影响数学成绩的提高.因此，利用多种思维技巧优化高中数学解题方法是非常重要的.

一、直接法

在解答数学习题的过程中，直接法是一种比较简单的解题思维技巧.这种方法主要适用于填空和计算类型的数学习题.它的解题思路是根据题目中所给出的已知条件，直接进行相关的数学计算，从而得出答案.在使用直接法解题时，教师需要引导学生认真阅读题目，理解题目中所给的条件和要求，再根据所学的相关知识，利用已知条件进行计算，最终得出答案.下面以一道例题说明直接法的具体应用.

这个例题的解答使用了等差数列的相关知识，按照一定的顺序进行计算，最终得出答案.虽然直接法是一种简单易行的解题方法，但是在面对难度较大的数学习题时，它的适用性和实用性都会受到限制，且由于考试时间有限，虽然某些题目能够通过考虑所有条件进行直接求解，但其条件众多、计算步骤繁多，并不利于应试.不仅如此，直接法对于理解题目陈述的准确性和清晰度有较高要求，若题目陈述不清晰或提供的信息不足，则无法进行直接计算.

二、构造法

构造法是一种解决数学问题的思维技巧，在解答问题时，通过运用已知条件和隐藏条件，构造出与问题相关的模型和方程式，从而找到问题的解决方法.在数学学习中，构造法可以被应用于各种高中涉及的数学问题，如代数、几何、概率，等等.下文将深入探讨构造法的原理和实际应用.

在构造法中，理解问题的已知条件和隐藏条件是解题的关键.已知条件是解题的出发点，它是题目中明确给出的信息，隐藏条件则需要通过对已知条件的深入分析和推断获取.需要注意的是，隐藏条件往往不是直接给出的，而是需要学生自行推断和构建的.因此，教师需要引导学生在解题过程中注重思考和分析，从已知条件中找到更多的信息，构建新的条件，以便更好地解决数学问题.

总的来说，构造法是一种非常实用的数学问题解决方法.通过理解问题的已知条件和隐藏条件，构建问题的模型和方程式，以及计算问题的解答，可以有效提高解答数学问题的速度和准确性.在数学学习中，学生应该积极运用构造法解决各种数学问题，提高数学学习的效果和成果.

三、换元法

换元法是高中数学中常用的一种解题技巧，常适用于代数和三角函数的问题.换元法的核心思想是通过变量的替换，将原问题转化为一个更加简单或更易于处理的问题.在高中数学中，换元法经常被用于解决方程问题.

即原不等式成立.

除了代数换元法，三角换元法也是高中数学中常用的一种技巧.在求解三角函数的问题中，可以通过换元法将问题转化为其他三角函数的问题，从而简化计算.

还有一些特殊的换元方法，例如指数换元法和逆函数换元法.在解决指数函数的问题时，学生可以采用指数换元法，将指数函数转化为自然对数函数，从而简化计算.当选择适当的换元方式时，学生需要对原问题进行深入思考和分析.有时候可通过观察问题的特点和结构，找到一些特殊的换元方式，从而使问题得到更好地解决.同时，对于某些问题，可能需要多次换元，才能使问题得到合理的简化，达到解决的目的.因此，在使用换元法时，学生需要灵活运用，结合具体问题进行思考和分析.在注意新问题与原问题之间的关系时，需要注意避免出现漏解或重解的情况.有些问题可能会出现多组解，而有些问题则可能只有唯一解.因此，在解决问题时，学生需要对每个解进行检验和确认，以确保答案的正确性.此外，在进行换元后，可能会出现新问题过于复杂，难以直接处理的情况.这时候，学生可使用代数化简或三角函数公式等方法，对新问题进行简化和转化.在进行简化和转化时，学生需要注意保持问题的等价性和正确性，避免引入新的问题或矛盾.

四、数形结合法

数形结合法是一种应用广泛的数学问题解答技巧.在解答数学问题的过程中学生经常会遇到需要用到图形辅助解题的情况.数形结合法能够将数学问题与对应的图形相互联系，将抽象的数学问题转化为具体的图形，从而更加直观地了解数学问题的性质和规律，最终得出数学问题的答案.

解题思路 该题并不需要详细求解f（x）和g（x）的表达式，而是直接利用“函數的性质及其图像”的相应知识点进行解答，通过明确奇函数和偶函数的不同图像特征，绘制大致图像以帮助理解关键趋势与数值.首先，教师可引导学生利用导数关系推导f（x）g（x）的性质.接着，由已知条件推断函数y=f（x）g（x）在特定区间的性质，即为奇函数.最后，利用奇函数的性质，画出其关于原点对称的大致函数图像（如图1），确定函数y=f（x）g（x）在[-b，-a]上的增减情况，并得出其在[-b，-a]上为增函数，且有最大值5.

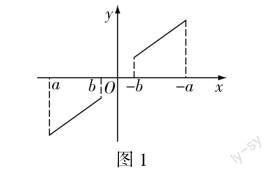
在使用数形结合法时，首先，学生需要注意绘图的准确性和图像的合理性，并充分理解问题的数学含义.只有理解了问题的数学含义，才能准确地绘制图形.同时，学生还需要具备较高的几何直观能力，能够将数学问题转化为具体的几何图形，以便更好地理解和解决问题.其次，学生需要注意细节和准确性.在绘制图像和进行计算的过程中，学生需要注重细节，特别是对于图形的测量和计算过程，需要尽可能准确.不仅如此，学生在解题过程中也需要注意符号的使用，确保符号的一致性，避免出现符号混淆等错误.此外，学生还需要不断练习和思考.

综上所述，数形结合法是一种有效的解题方法，它能够帮助学生更好地理解数学问题，并提高学生解决问题的能力.在教学过程中，教师需要注重培养学生的数学思维能力和几何直观能力，帮助学生掌握数形结合法的技巧，并及時纠正学生的错误，以便提高教学效果和学生的学习效果.

五、特例法

特例法是数学中一种常用的解题方法，也被称为取特殊值法或代数特例法.该方法通过寻找一些特殊的数值，使得问题得以简化，从而更容易得到正确的解答.特例法在解决复杂的数学问题时非常有效，特别是在考试的选择题中，可以帮助学生快速选择正确答案，以达到应试需要.以下将进一步介绍特例法的思路和应用场景.特例法的思路可以用以下几个步骤概括：首先，根据问题中的已知条件，确定可以取特殊值的变量或参数，然后将这些变量或参数取一个具体的特殊值，使得问题得以简化.最后，通过解决简化后的问题，找到原问题的解答.

总的来说，特例法是一种非常实用的解题方法，可以帮助学生在解决复杂的数学问题时更加高效地得到正确的解答.同时，教师在教学过程中也可以使用特例法帮助学生理解题目.在多项选择题、填空题中，特例法更是一种快速解题的利器.虽然特例法在一些特定情况下可以有效地解决问题，但是它的局限性也非常明显.特例法往往只适用于特定的情况，不能得到通解的正确性.特例法可能会产生一些偏差或误导.因此，在使用特例法时，教师需提醒学生谨慎权衡其适用性和实用性，尽量避免使用不必要的特例法.

结 语

综上所述，文章介绍了五种在高中数学学习中应用广泛的解题思维技巧：直接法是一种最基础的解题思维技巧，它强调直接使用题目中给出的条件进行计算；构造法通过构造一个具体的数学对象来推导出结论；换元法是将原问题转化为另一个等价的问题来解决，使得原本复杂的问题变得简单；数形结合法是将数学问题与图形结合起来，通过图形的直观性来理解和解决问题；特例法通过举出一些特殊情况，从而发现问题的规律和解决方法，教师也可利用特例法帮助学生理解定理.

【参考文献】

[1]刘娜娜.通过多种思维技巧优化高中数学解题研究[J].数理化解题研究，2023（6）：29-31.

[2]刘慧.基于深度学习的高中数学新教材单元教学实施路径分析[J].读写算，2022（32）：119-121.

[3]马春霞.在高中数学教学中提高学生创新能力浅谈[J].读写算，2022（29）：25-27.