中华优秀传统数学文化融入初中数学教科书的内容分析

郭华佳　童莉

［摘  要］ 中华优秀传统数学文化从文化形态转化为教学形态，有利于发挥数学学科的育人功能，传承民族文化. 文章选取北师版、人教版初中数学教科书为研究对象，从内容类型、呈现方式、运用方式、认识水平四个维度进行统计分析，发现：中华优秀传统数学文化内容比例失衡，呈现方式单一，运用方式简单化，认知水平不高. 建议优化中华优秀传统数学文化内容，发挥中华优秀传统数学文化的教育功能，加强中华优秀传统数学文化感悟.

［关键词］ 中华优秀传统数学文化；初中数学教科书；学科育人

2021年教育部印发的《中华优秀传统文化进中小学课程教材指南》（以下简称《指南》），强调中华优秀传统文化的铸魂育人功能，提出结合学科特点，实现中华优秀传统文化“3+2+N”全科覆盖. 《义务教育数学课程标准（2022年版）》也提出要“关注数学学科发展前沿与数学文化，继承和弘扬中华优秀传统文化”［1］. 因此，中华优秀传统数学文化融入课程教学是数学学科落实《指南》精神的重要体现，更是数学学科育人的时代号召. 教科书是课程内容的载体，研究教科书中中华优秀传统数学文化的融入现状，探讨如何推进中华优秀传统数学文化教学的开展具有重要意义. 基于此，笔者拟对初中数学教科书中的中华优秀传统数学文化内容进行分析.

研究设计

1. 研究对象

本研究的对象为本地使用较广泛的2012年人民教育出版社出版（简称人教版）和北京师范大学出版社出版（简称北师大版）的义务教育数学课程标准实验教科书（7—9年级），共12本.

2. 研究方法

本研究采用内容分析法，参考已有研究维度构建分析框架，对教科书中的中华优秀传统数学文化内容进行划分，统计各类别数量，结合定量和定性分析得出结论.

3. 分析框架

通过梳理文献发现，内容类型、呈现方式、认知水平是将中华优秀传统数学文化融入数学教科书时关注的焦点［２－４］. 此外，运用方式是影响中华优秀传统数学文化教学效果的重要因素. 因此，本研究将从内容类型、呈现方式、运用方式和认知水平四个维度对初中数学教科书中中华优秀传统数学文化内容进行分析.

参考董毅在《数学思想与数学文化》一书中对数学思想文化的定义［5］，并结合数学教科书的具体情况，本研究将中华优秀传统数学文化划分为数学历史、数学思想方法、数学应用、数学精神、数学游戏五类. “呈现方式”借鉴姜浩哲对栏目的划分，根据所处栏目将其分别归于贯穿性正文、背景性正文、阅读性专栏、例题与习题［4］. “运用方式”参照汪晓勤等人对数学史的划分［6］，并进行更贴切的解释. “认知水平”按中华优秀传统数学文化的认知水平划分为了解性、无联系程序性和联系程序性，逐级递增［7］. 具体统计指标如表1所示.

研究结果与分析

1. 内容类型

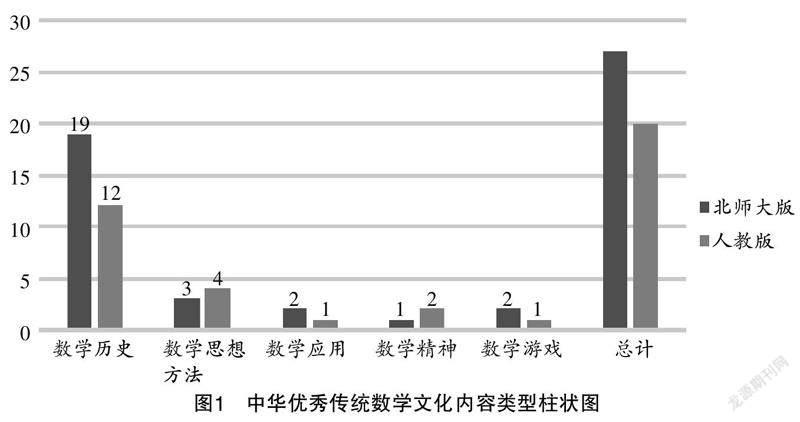
由图1可知：从总量来看，北师大版中华优秀传统数学文化素材数量多于人教版；从内容分布来看，中华优秀传统数学文化的主要类型是数学历史，北师大版、人教版分别包含19处、12处，其次是数学思想方法，对数学应用、数学精神、数学游戏关注较少，存在着严重失衡.

教科书中的中华优秀传统数学文化的取材在一定程度上影响实际教学的价值取向. 数学历史是中华优秀传统数学文化的重要组成部分，在数学教学中介绍一些数学知识的发展历史，有利于激发学生的学习兴趣，这属于中华优秀传统数学文化的历史价值层面. 实际上，数学的文化价值不仅表现在知识本身的发展历史，还在于知识背后所蕴含的数学思想、数学精神以及它的应用价值. 中华优秀传统数学文化具有明显的东方特点，“正负术”“勾股定理的无字证明”“一元二次方程的几何解法”“海岛测高”等内容蕴含了中华优秀传统数学文化算法化、模型化、数形结合的特点，对学生的思想启迪具有重要作用. 教科书中将一次函数模型与“漏刻”工作原理相联系，有利于学生了解数学与社会发展的相互作用，感悟古代人民的数学智慧，其教育价值远超于数学知识本身.

2. 呈现方式

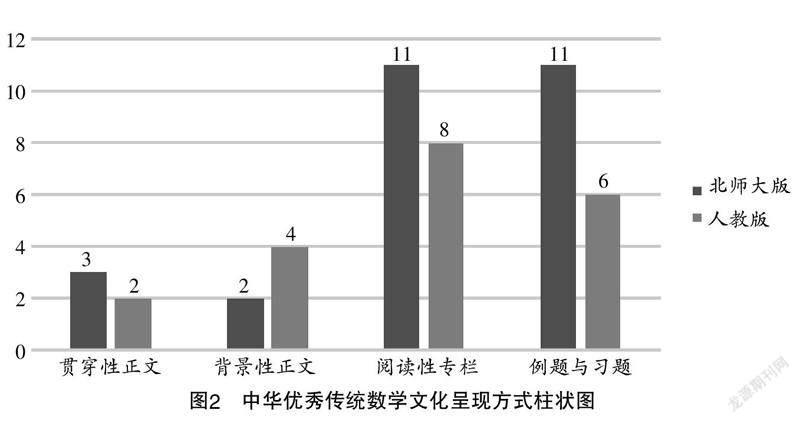
根据图2可知：初中数学教科书中对中华优秀传统数学文化主要编排在“阅读性专栏”和“例题与习题”栏目中，北师大版包含了11处阅读材料和11道古代数学名题，人教版包含了8处阅读材料和6道古代数学名题. 贯穿性正文内容较少，主要是以古代数学游戏为载体设置探究活动.

事实上，呈现方式的不同决定了其在数学教学中具有不同的功能. 在阅读性专栏或背景性正文中介绍我国古代数学的辉煌成果，对激发学生兴趣、开阔学生视野，帮助学生感悟中华民族智慧有重要作用，例如初中数学教科书中以“杨辉三角”为载体，引导学生探究（a+b）n展开式系数的规律，不仅强化了学生对“整式的乘积”有关知识的认识，还加深了学生对“杨辉三角”的理解，让学生感受到了数与形之间的奥秘.

初中生正处于由感性认识到理性分析的过渡期，古代数学名题通常是基于经验或任务导向的，在数学教学中编排我国古代数学经典名题，有利于降低数学问题固有的抽象性，帮助学生了解传统社会日常、风俗民情. 北师大版在“二元一次方程组”内容中编排了多个生活化的数学问题，如“牛羊各值金几何”，这反映了当时社会的物价情况.

3. 运用方式

由图3可知：北师大版和人教版中的中华优秀传统数学文化素材以复制式和附加式融入为主，占比高达74.1%和60%；体现数学史古为今用的顺应式内容，两版本数学教材中分别包含4处、5处，而点缀式内容较少. 值得注意的是，体现数学知识发展过程的重构式内容严重不足，北师大版仅包含2处，人教版未出现重构式内容.

中华优秀传统数学文化的运用方式直接影响教学效果，由于附加式材料和直接引用古代数学问题的复制式材料不需要进行任何加工改动，内容浅显，故更加容易融入初中数学教学中. 但两者的运用水平均相对较低，无法体现数学家对知识的火热思考. 对中华优秀传统数学文化素材进行一定程度的加工的顺应式，使材料具有适合课堂教学的情境或属性，有利于学生接受和理解中华优秀传统数学文化和成就. 作为最高水平的重构式，通过重构知识发展过程，积极引导学生了解知识的发生、发展过程，有利于提高学生分析问题、解决问题的能力. 例如北师大版在“一元二次方程的幾何解法”内容中展示了阿尔·花拉子米和赵爽的几何解法，将逻辑演绎追溯到归纳演绎，让学生在归纳中体会不同时空的数学家对同一课题的探索，进一步开拓思维.

4. 认知水平

由图4可知：北师大版和人教版中的无联系程序性材料数量最多，分别包含13处、8处. 其次是了解性材料，分别包含9处、8处. 联系程序性材料占比最小，分别包含5处、4处，约占中华优秀传统数学文化内容总量的20%. 中华优秀传统数学文化的认知水平设置合理，充分考虑了初中学生的认知水平.

进一步，我们发现认知水平的设置与其所在位置有一定关系. 首先，中华优秀传统数学文化借助旁注的方式帮助学生了解数学的知识源流；然后，在知识训练中引入古代数学问题，让学生在古今解法的对比中感受创造性智慧、巩固新知，进一步渗透中华优秀传统数学文化；最后，当学生对知识掌握到一定程度后，教科书在章节末尾设置拓展性阅读或数学探究活动来增强中华优秀传统数学文化的深度，让学生深刻感悟古代人民的创造性智慧. 例如《海岛算经》中的“测高问题”对学生的知识储备有一定的要求，难度较大. 而刘徽早在公元263年就利用线段之间的比例关系得到了精确的结果，显示了我国古代测量数学的进步，这一内容的融入有利于学生深刻感受中华优秀传统数学文化的魅力，增强民族自信心.

研究启示

1. 多元挖掘文化资源，优化中华优秀传统数学文化内容

两个版本初中数学教科书中的中华优秀传统数学文化存在着严重的类型别分布不均的问题，侧重于知识性成分，对观念性成分和数学生活化缺乏关注. 事实上，观念性成分可以从精神层面上影响学生学习数学的信念、行为和价值观［8］，培养学生的良好品质，其教育价值高于知识本身. 因此，教师首先需要积极开发中华优秀传统数学文化资源，以多角度、多领域进行展示，增添丰富性和生动性；其次，教科书对中华优秀传统数学文化内容的研究浅尝辄止、系统性不强，可以专题的形式进行整合，如刘徽在代数方面的贡献、宋元数学“几何代数化”的卓越表现、半符号代数的建立（天元术和四元术）.

2. 有机融入教学活动，发挥中华优秀传统数学文化功能

以数学课程标准为依据，科学解构中华优秀传统数学文化在数学教科书中的呈现方式以及教学要求，可以更好地实现中华优秀传统数学文化从课程形态向教学形态的转化. 中华优秀传统数学文化的教学要与现有的数学课程内容有机结合起来，把凸显中华优秀传统数学文化思想内涵的课程内容视为教学重心，注重将中华优秀传统数学文化内容与问题探究、项目式学习、数学实验等数学活动有机结合，在教学各环节进行有机渗透，并在教学时辅以图片、影像等多元化手段进行讲解，为学生营造“沉浸式”学习氛围，充分发挥中华优秀传统数学文化的育人功能.

3. 合理设置认知梯度，加强中华优秀传统数学文化感悟

两版本初中数学教科书中中华优秀传统数学文化的认知水平不高，联系程序性材料占比较小，大多数内容是学生课后自主浏览便可快速了解的古代数学成果，但过多的了解性材料极易使中华优秀传统数学文化教学陷入广而不深的形式主义泥潭. 因此，教师在中华优秀传统数学文化教学中可适当调整中华优秀传统数学文化的認知水平，加强学生对中华优秀传统数学文化的感悟. 例如人教版在“有理数的加减法”内容中要求学生仿照完成含负数的幻方，但完成难度系数低，难以使学生与材料产生共鸣. 对此，教师可引导学生自主探究三阶幻方所隐藏的数学规律，进一步领悟中华优秀传统数学文化背后的知识原理后再解决相关问题，并适当介绍我国南宋数学家杨辉关于幻方的研究成果，进一步感受幻方构造中神秘而深远的数学思想.

参考文献：

［1］ 中华人民共和国教育部. 义务教育数学课程标准（2022年版）［Ｍ］. 北京：北京师范大学出版社，2022.

［2］ 曹一鸣. 中华优秀传统数学文化进中小学数学课程：从意义到实施［Ｊ］.教育研究与评论，2022（06）：46-49.

［3］ 陈云龙，任建英，曾莹. 中华优秀传统文化教育发展的探讨［Ｊ］. 课程·教材·教法，2019，39（12）：89-95.

［4］ 姜浩哲. 我国传统数学文化融入教科书的价值、现状与展望：以人教版小学数学教科书为例［Ｊ］. 课程·教材·教法，2021，41（01）：98-104.

［5］ 董毅. 数学思想与数学文化［Ｍ］. 合肥：安徽大学出版社，2012.

［6］ 蒲淑萍，汪晓勤. 数学史怎样融入数学教材：以中、法初中数学教材为例［Ｊ］. 课程·教材·教法，2012，32（08）：63-68.

［7］ 李保臻，陈国益，张黎娜. 我国传统数学文化融入高中数学教科书：现实样态与教学启示：以2019年人教A版高中数学教科书为例［Ｊ］. 内蒙古师范大学学报（教育科学版），2022，35（01）：102-108.

［8］ 朱卫平. “数学文化”渗透之思考：基于人教版教材“阅读与思考”栏目的统计与分析［Ｊ］. 教学月刊（中学版），2011（12）：38-39.