串行式混合类型航道船舶交通组织优化

王志强 张新宇 李倍莹 王婧贇

(大连海事大学海上智能交通研究组 辽宁 大连 116026)

0 引 言

随着水路运量的不断上升以及港口船舶的大型化、高速化、密集化,港口航道类型开始由单一类型向多样化、复杂化的混合类型趋势发展,使得现有规模以上港口出现了单、双向航道通过能力不足、航道中船舶交叉与会遇频繁,大大增加了船舶交通组织与管理的复杂性。例如2019年,宁波舟山港累计完成货物吞吐量11.19亿吨,成为目前全球唯一年货物吞吐量超11亿吨的超级大港,船舶进出港约71万艘次,每天交通流量超过2 000艘次[1],这些船舶主要通过虾峙门等五个主要航门,客船、危险品船、液化天然气船、集装箱船等船种齐全,此外小型船舶、渔船数量众多,造成核心港区主要航道通航环境十分复杂。鉴于此,船舶交管部门尝试利用基于单一类型航道(单向/双向航道)的混合航道交通组织方式来提高船舶交通的安全及效率。混合类型航道一般存在两种较为典型的类型：(1) 串行式简单混合类型航道(黄骅港煤炭港区,图1；拉普拉塔港口,图2)。此类型航道仅在串行方向上存在单/双航道混合情况。(2) 交叉式复杂混合类型航道(宁波舟山港混合航道,图3)。此类型航道基于串行式简单混合类型航道存在多条单/双通航航道交叉的情况。

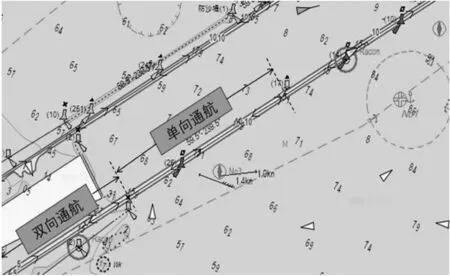
图1 黄骅港(煤炭港区)混合航道

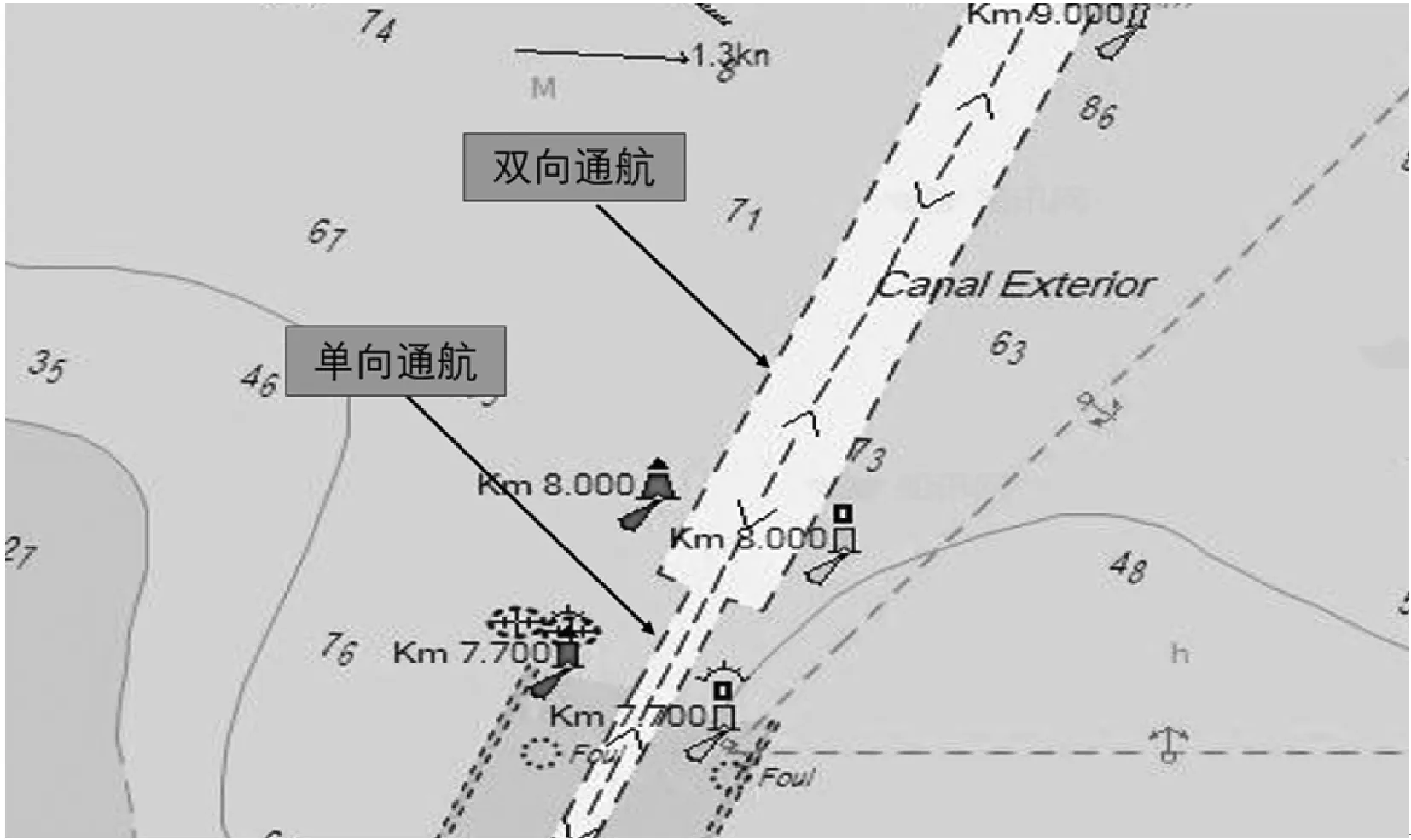
图2 拉普拉塔港口混合航道

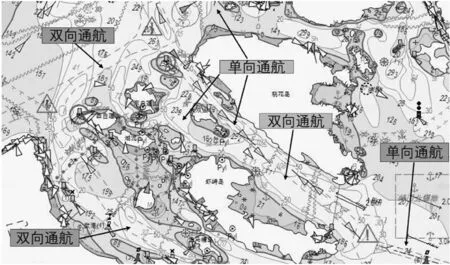
图3 宁波舟山港混合航道

近年来,国内外针对混合航道水域船舶交通组织的相关研究较少,但对于单一航道类型(单向/双向航道)条件下船舶交通组织问题有部分研究。郑红星等[2]针对单向航道散货港口的泊位利用率,考虑船舶间安全距离、进出港时段交替条件和成簇进出港规则等约束,以进港船舶总等待时间最小为目标,构建了混合整数线性规划模型。Jia等[3]基于单向航道通航能力的特点,以进出港船舶的惩罚费用为目标,建立了混合整数线性规划数学模型。张新宇等[4]考虑船舶属性和船舶交通状况等因素,分别构建了以总船舶调度时间和总船舶在港等待时间最小为目标的单和双向航道船舶交通组织优化模型。Uluscu等[7]考虑船舶等待时间长短和船型优先权等因素,建立了双向通航条件下船舶进出港数学模型。通过分析,单一类型航道船舶交通组织问题须考虑进出港船舶流量转换、单/双向通航模式转化、船舶间安全时隙以及警戒区会遇船舶协调避让等问题,相比之下,混合类型航道条件下船舶交通组织问题除要基于单一类型航道船舶交通组织问题外,还须特别考虑单向/混合通航模式转化、混合航道异类子航道间通航模式切换、港池连接水域船舶交通冲突等问题,以确保船舶在混合航道单向子航段和双向子航段、航道重要交通冲突区域的航行安全性和效率性。在船舶交通组织优化算法方面,Meisel等[8]针对双向航道船舶交通调度问题,提出了变航速、侧线段容量和船舶等待时间限制的优化策略,并采用启发式算法求解。Lalla-Ruiz等[9]针对上海外高桥水域双向航道,设计了混合整数线性规划数学模型并利用模拟退火算法进行求解。Sluiman[10]提出了一种船舶交通调度算法,用以应对双向航道货物吞吐量的负面影响。Zhang等[11]考虑船舶调度的安全性、效率性和公平性,协调航道和泊位资源构建了船舶交通调度优化模型并采用模拟退火和遗传算法求解。通过归纳发现所采用的求解算法大都为模拟退火和遗传算法等常规的智能优化算法,其在面对较为复杂的船舶交通组织优化问题时,常存在收敛速度慢、陷于局部最优等情况。

综上,国内外缺少针对港口混合类型航道船舶交通组织问题的研究,鉴于此,本文通过调研国内外港口混合类型航道,抽象出一种串行式简单混合类型航道作为研究对象。在现有船舶交通组织优化理论基础上,构建以单向/混合通航模式转化、混合航道异类子航道间通航模式切换、港池连接水域船舶交通冲突消解等为约束的串行式简单混合类型航道船舶交通组织优化模型,并提出一种Spark分布式多目标遗传算法,高效地求取模型的最优方案。

1 模型建立

1.1 问题描述

通过调研混合航道船舶进出港调度流程,基于现有船舶交通组织理论,提炼出串行式混合航道船舶交通组织的关键问题包括以下三点：

(1) 单向/混合通航模式转化：混合航道水域船舶通航模式受到航道物理条件、船舶类型(船型尺度、船舶载态、船舶吃水及载运危险物等)、水文气象等因素影响,这些因素的综合作用使得混合航道在单向通航模式与混合通航模式之间转换。

(2) 混合航道异类子航道间通航模式切换：通常情况下,一般3、5万吨左右的小船可双向通行,而大型客船、油船只能单向通行,同时此类航道通常会在异类子航道分界处设置会遇点,当小船和大船会遇时,先让小船在会遇点抛锚或漂航等候直到大船通过再航行。

(3) 港池连接水域船舶交通冲突消解：连接水域在航道与港池之间,形成梯形可航水域,此处多船会遇情况下连接水域的富余程度略显不足、可航水域狭小,同时船舶进出方向、所靠泊位、载态各异、速度较低,操作性差,所形成的交通局面极为复杂。

基于以上对串行式混合类型航道水域船舶交通组织问题的分析,得出串行式混合类型航道船舶交通组织优化的关键在于确定最佳的船舶进出港序列,确保船舶在单向/混合通航模式转化时、混合航道异类子航道间通航模式切换时,以及港池连接水域航行时的安全性、效率性、连续性。为便于建模，设置航道关键点1-6,其中关键点2和5分别取1-3和4-6的中点,如图4所示。

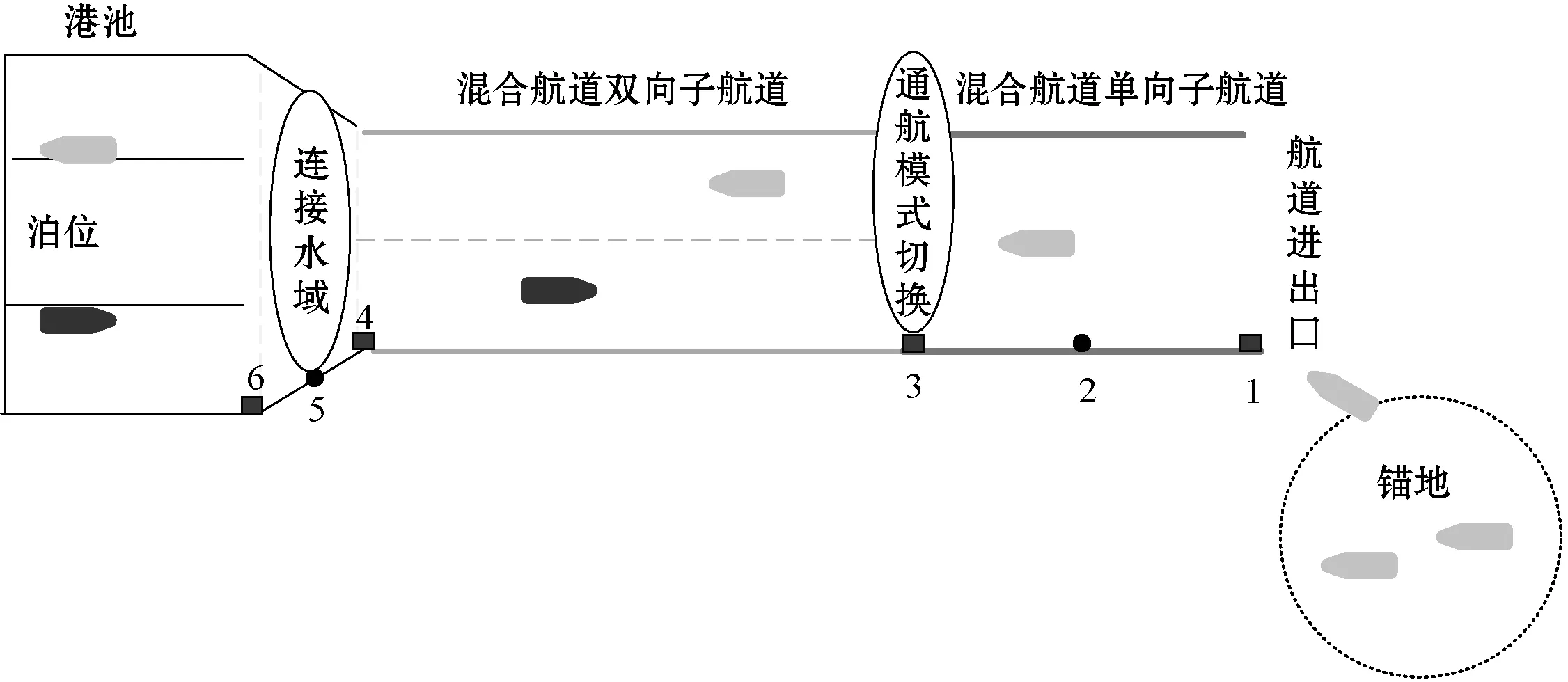
图4 串行式简单混合航道示意图

1.2 模型假设

(1) 进港船舶调度起止时间为锚地到泊位,出港船舶调度起止时间为泊位到出航道位置。(2) 水文气象条件满足船舶进出港作业要求。(3) 引航员、拖轮、锚地容量充足,不影响船舶进出港计划。(4) 船舶靠泊作业计划已提前制定,即不考虑泊位指派问题。

1.3 变量及符号定义

N:船舶集合N={1,2,…，n},n为按照船舶申请进出港时间顺序确定的船舶编号。

Tpi:船舶i申请进出港时间,也即船舶完全就绪时刻,∀i∈N。

Tsi:船舶i开始被调度时刻,∀i∈N。

Tfi:船舶i完成进出港时刻,对于进港船,指船舶停靠泊位时刻；对于出港船,指船舶出航道时刻,∀i∈N。

Tg0:船舶最小同向安全时隙。

Tg1:船舶最小异向安全时隙。

Tg13:表示混合航道单向子航段(关键点1-3)的平均时隙。

Tg46:表示港池连接水域(关键点4-6)的平均时隙。

Dk:航道关键点k和k-1之间的距离,D1表示锚地到上航道位置的距离,∀k∈{1,2,…,6}。

vi:船舶i在航道航行速度,Avi和Bvi分别指船舶在锚地和港池航行平均速度,∀i∈N。

ΔBdi:船舶在港池关键点6和停靠泊位之间距离,∀i∈N。

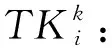
IOij=0表示船舶i和j进出港方向相同,IOij=1表示船舶i和j进出港方向不同。

Xi:船舶i航行方向,Xi=1为进港，Xi=0为出港。

y:船舶航行模式,y=0为单向通航，y=r为混合通航,其中:r=1指混合通航模式下船舶在单向子航段航行,r=2指混合通航模式下船舶在双向航段航行。

1.4 优化模型

基于前文问题分析,本文构建的串行式简单混合航道船舶交通组织优化模型(Ship Traffic Organization Optimization Model Under Serial Simple Mixed Channel,STOOMSSMC)如式(1)-式(8)所示。

(1)

s.t.

Tpi≤Tsi,∀i∈N

(2)

⋮

(3)

∀i∈N

(4)

(5)

(6)

(7)

(8)

式(1)为目标函数,表示总船舶进出港调度时间最少。式(2)至式(8)中进出港船舶i均在j之后调度。式(2)-式(4)各项分别表示每艘船舶的开始调度时间不早于其完全就绪时间、每艘船舶调度结束时间等于其航行过程中各个关键点之间的航行时间累加、进出港两船在航道混合通航模式/单向通航模式下航行保持同向安全时隙以确保船舶在航行过程中的时间安全性和连续性。式(5)为模式切换约束,用于判断当混合通航两异向船舶切换到混合通航模式下单向子航段航行时,通过调整船舶到达航道关键点2的时刻以保证两船在整个混合通航单向子航段只能保持单向航行。式(6)为港池连接水域交通冲突消解,用于避免两异向船在港池连接水域产生会遇冲突。式(7)和式(8)为模式转换约束,混合通航模式和单向通航模式转换发生在进航道位置(关键点1)和港池与航道交界位置(关键点4),其中式(7)表示混合通航模式分别转换为单向进港或单向出港通航模式,式(8)表示单向进港或单向出港通航模式转换为混合通航模式。

2 模型求解

近年来比较热门的并行技术Spark是一种基于内存计算的开源分布式并行计算框架,其特有的弹性分布式数据集RDD(Resilient Distributed Datasets)运算机制是一种具备高效容错性的分布式弹性存储系统[12],它将大量数据分布式地存储在不同计算节点的本地内存中,使得每次迭代的中间结果可保存在内存中直接供下一次的迭代运算调用。

本文针对STOOMSSMC模型特点,基于Spark并行计算框架的多计算节点本地内存化等优势,结合NSGA-II种群、遗传操作天然并行性特点[13],借助于Scala编程语言使Spark分布式计算框架嵌入NSGA-II算法实现一种Spark分布式多目标遗传算法(Nondominated Sorting Genetic Algorithm II on Spark,SK-NSGA-II),以便将全部种群分散在多个子种群中,在多节点上并行地执行遗传算法的选择、交叉和变异等操作,从而保证存在子种群可避免淘汰优秀个体,以便继续有效地进行后续遗传操作,可一定程度上防止算法过早收敛到局部最优值的现象,大大提高算法的搜索范围和执行速度。SK-NSGA-II设计流程如图5所示,SK-NSGA-II中遗传算子操作如算法1所示，Spark算子操作步骤如算法2所示。

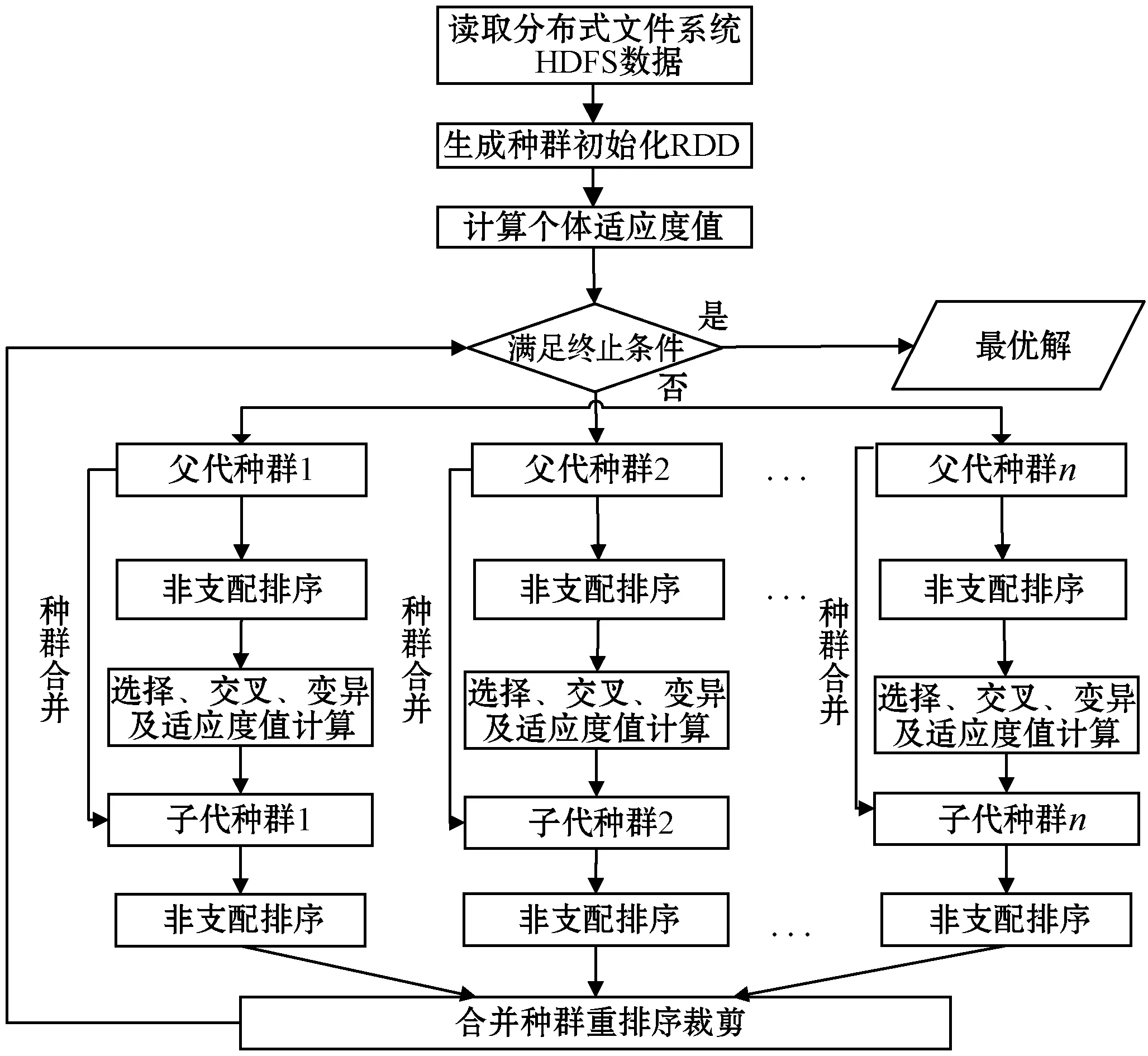
图5 SK-NSGA-II设计流程

算法1遗传算子操作

Step1船舶交通组织染色体编码采用排列编码。对于一条染色体,每一个基因位代表船舶的编号,基因位的顺序代表船舶进出港的顺序。

Step2适应度函数。对于本文船舶交通组织模型的目标函数,数值越小则代表越优,因此取个体目标函数值的倒数作为个体的适应度值,并将模型中各约束条件转化为适应度函数的惩罚项。

Step3其他遗传算子。选择算子采用锦标赛选择法,交叉算子采用部分映射交叉的方法,变异算子采取二元变异方法。

算法2Spark算子操作

Step1通过SparkContext实例对象中textFile函数从HDFS(分布式文件系统)中读取n个排列编码的种群小文件,生产RDD,随机分配到各个节点,以作为初始代种群。

Step2使用Spark的API函数Map在各个节点上进行求取个体适应度值,并以形式保存到新生成的RDD。

Step3对Step2产生的RDD进行去重,并使用Spark的API函数mapPartitions对每个分区个体先进行非支配排序,再循环执行选择、交叉、变异操作生产子代种群,然后利用Scala的API函数map依次进行适应度值求取和子父代种群合并操作。

Step4对合并后的种群依次进行非支配排序操作和种群裁剪操作,更新父代种群,直到满足终止条件,输出最优解。

3 模型与算法验证

3.1 模型合理性分析

本文从实际出发，基于国内外实际混合航道实例，抽象出一种含有混合航道共性特征的串行式混合类型航道。例如，宁波舟山港混合航道基于串行式混合航道，存在多条单/双通航航道交叉的情况，而国内黄骅港煤炭港区混合航道和国外拉普拉多混合航道均为串行式混合航道实例，该串行式混合航道具有全局双航段异类通航(单/双向通航)和局部单航段有条件双向通航等通航特点。以黄骅港煤炭港区串行式混合航道为例，具体来说，该航道由于船舶交通、自然地理等条件限制，按照《黄骅港煤炭港区航道双向通航推进会纪要》规定，航道22#浮筒附近上线处至32#浮筒口门位置航段船舶实行单向通航，其余航段船舶实行有条件双向通航，而本文所抽象出的混合类型航道对航道布置和走向、锚地和港池的位置及数量等特殊情况进行了简化，重点突出影响串行式混合航道通航效率的通航模式切换、港池连接水域冲突等关键因素。

基于抽象出的混合类型航道所构建的优化模型中，关于模型目标函数，混合类型航道各种因素的作用直接影响到港口船舶交通组织相关部门对进出港船舶调度的时间，从而关系到船舶在港作业的效率，鉴于此，本文选取的总船舶调度时间优化目标符合交通组织部门的需求；关于模型约束条件，影响混合类型航道船舶交通组织效率的因素区别于常规单一类型航道，主要表现在混合类型航道单向/混合通航模式转化、混合航道异类子航道间通航模式切换、港池连接水域船舶交通冲突等问题，鉴于此，本文优化模型充分考虑以上混合类型航道船舶交通组织问题，以保证进出港船舶在串行式混合类型航道航行的安全性和效率性。

因此，本文基于当前港口实际混合航道情况抽象出的串行式混合类型航道具有现实依据，且针对抽象出的混合类型航道所构建的优化模型具有合理性。

3.2 实验预处理

本文基于黄骅港煤炭港区(串行式简单混合航道)获取相应的实验仿真数据,建立30艘船舶交通仿真基础数据库,部分船舶数据如表1所示。

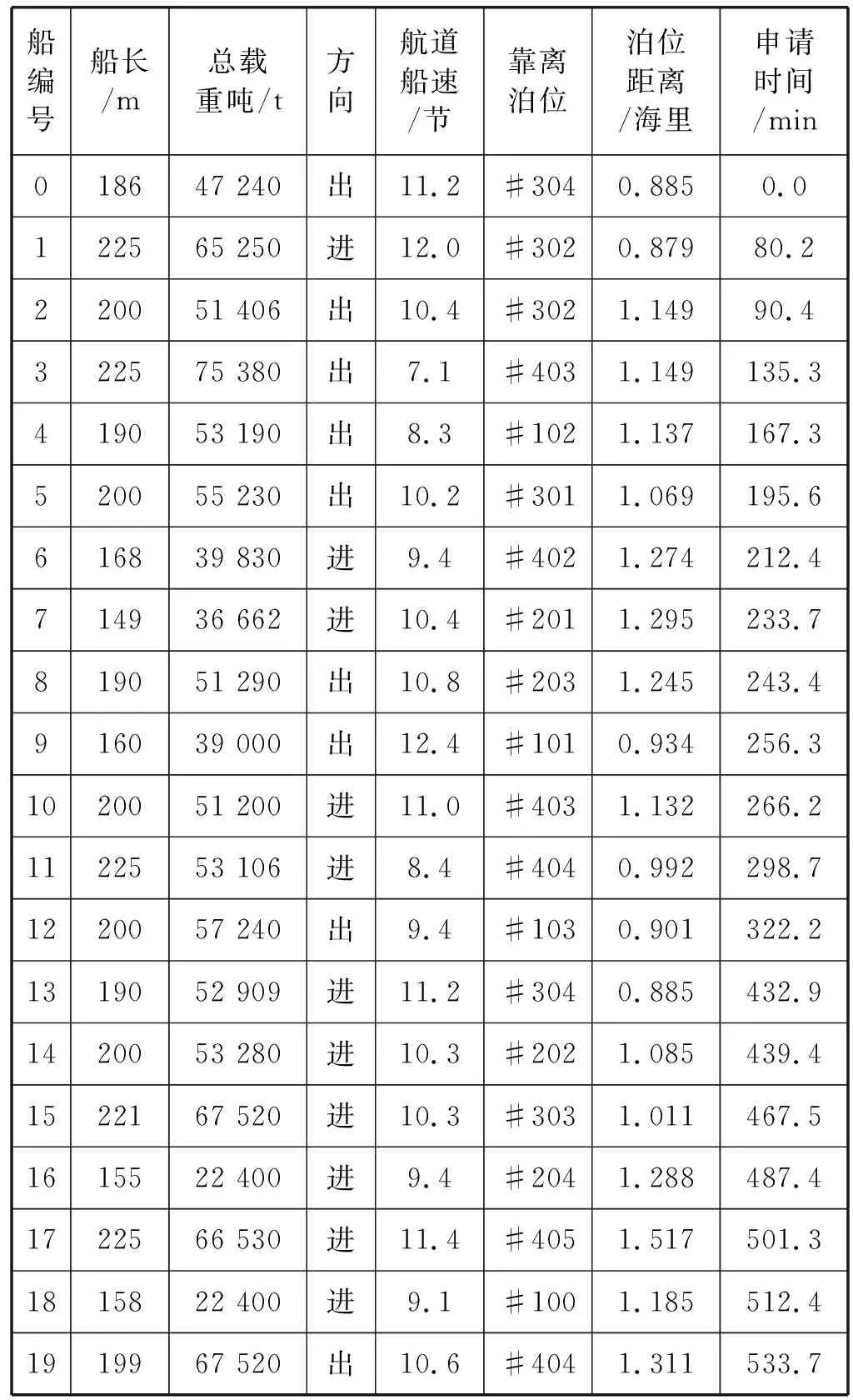
表1 船舶基础信息

此外,对模型及算法参数进行设置如下：设船舶调度时间从0时刻开始；基于黄骅港航道船舶安全间距(港区规定安全距离1.5海里)、锚地-关键点1(2.9海里)、关键点1-3(5.6海里)、关键点3-4(10.2海里)、港池连接水域范围(1.0海里)，按锚地、航道和港池船舶航行平均速度(依次对应4.9节,11.3节,3节)转换为对应的安全时隙并设定Tg0=Tg1=8 min、Tg13=30 min、Tg46=20 min(关键点3-4间航行时间按实际对应船速计算)；为测试算法收敛性和稳定性,对30艘船舶仿真实验重复进行50次；在多次实验基础上对模型求解的算法参数进行调优,设置SK-NSGA-II可读取的HDFS中种群小文件数30个,并可动态调整种群数以测试SK-NSGA-II和NSGA-II的性能,设置两种算法交叉概率为0.95,变异概率为0.05,终止代数300。

3.3 仿真结果及分析

(1) 算法性能分析。在对30艘船舶仿真实验重复进行50次基础上,从SK-NSGA-II和NSGA-II运行结果平均质量的统计、算法运行时间随种群规模和迭代次数的变化等角度,对两种算法收敛性、稳定性、运行时间等方面进行分析。50次仿真重复实验结果所得解的平均质量统计如表2所示,其中具有一般性和代表性的一次运行的结果如图6所示。由图6可以看出两种算法对模型求解出的目标值最优解及均值在不断地寻优,SK-NSGA-II下目标值的平均值变化较为均匀,且其目标值最优解于50代左右收敛到最优解,收敛速度明显快于NSGA-II,而NSGA-II目标值最优解最终陷入局部最优。这是因为SK-NSGA-II中的任一并行度都对应一个种群,并行度的扩增会使种群的计算能力和搜索范围得到提高,这在一定程度上避免了算法遗传操作早熟的现象发生。由表2可以看出SK-NSGA-II下实验运行结果的平均值和标准差均明显小于NSGA-II。相比之下,NSGA-II得到的目标值最优解分布离散程度较高、分布区间明显较大,说明NSGA-II目标值每一次寻优结果的差距较大,稳定性较差,而SK-NSGA-II50次实验寻优结果明显集中,稳定性较高。30艘船舶仿真实验下算法运行时间随种群规模和迭代次数的变化情况如图7和图8所示,可以看出,当迭代次数和种群规模较小时两种算法运行时间差距不大,原因是NSGA-II为单线程串行式运算,没有启动时间,而SK-NSGA-II下的Spark运行程序时首先要提交Spark应用程序任务,并初始化集群入口函数,分配节点资源,此外还涉及节点间网络通信问题,因此在算法执行的开始阶段Spark无法体现出其优势。然而随着迭代次数和种群规模的增加,SK-NSGA-II运行效率远高于NSGA-II，原因为此时程序运行的大部分时间都是程序计算,且SK-NSGA-II会将增加的数据分散到各个节点并行计算,从而大量节省算法计算的时间。

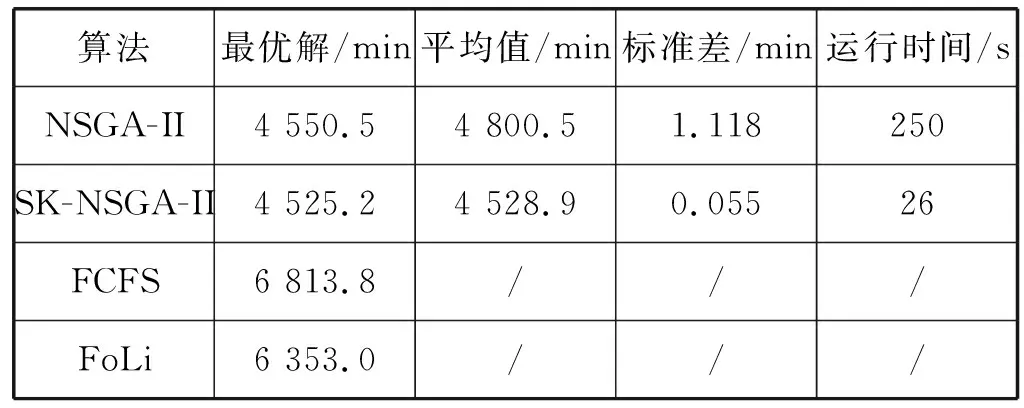
表2 实验结果统计情况

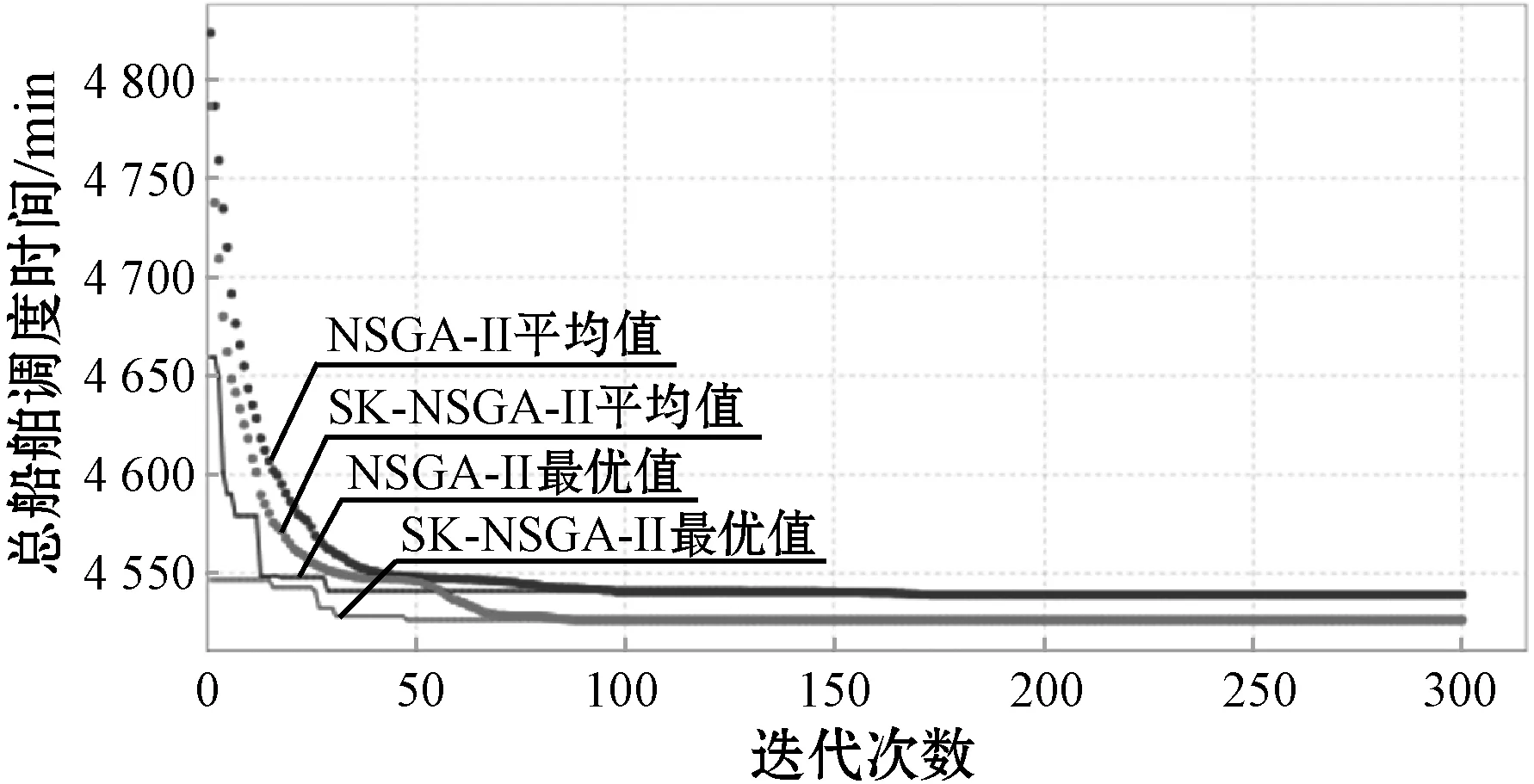
图6 SK-NSGA-II和NSGA-II运行结果

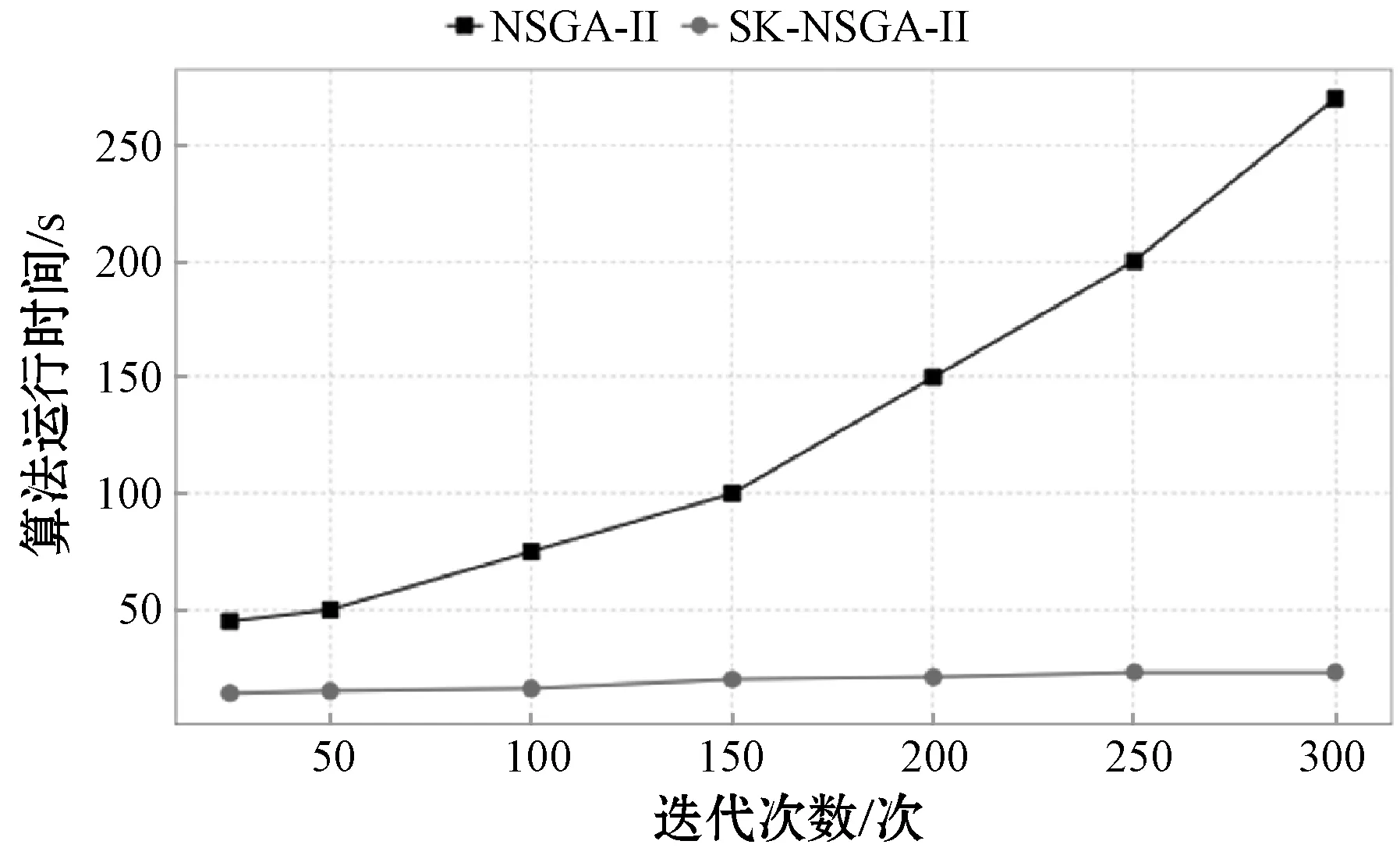
图7 算法运行时间与迭代次数变化

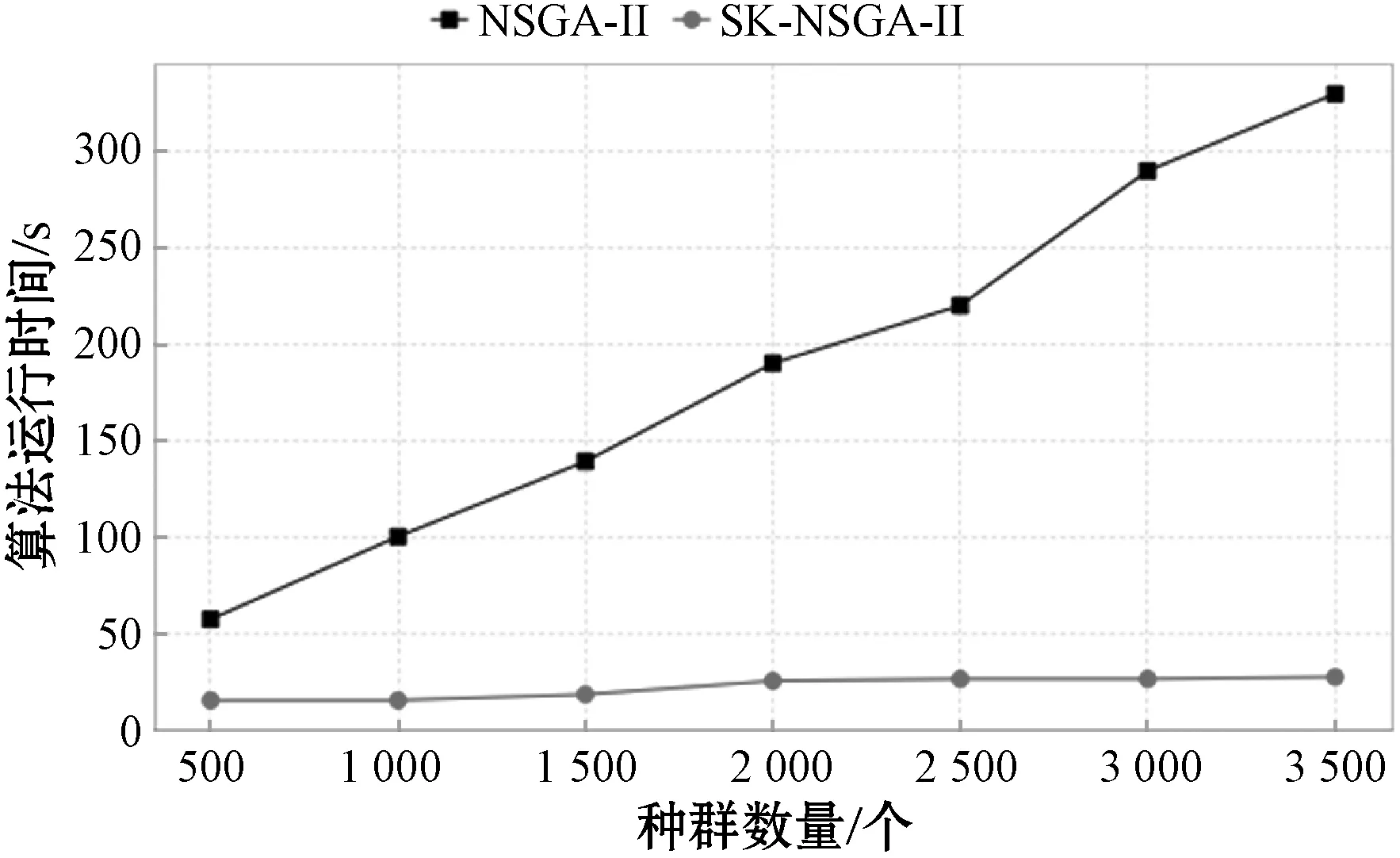
图8 算法运行时间与种群规模变化

(2) 模型有效性分析。为验证模型求解方案的有效性,将SK-NSGA-II求解出的最优方案与港口船舶交通组织相关部门常采用的FCFS方法(First Come First Served)和FoLi方法(First out Last in)进行对比,其中,船舶进出港序列如下：SK-NSGA-II(0,13,19,3,28,12,21,7,15,27,5,2,29,1,26,20,10,4,24,14,9,16,18,23,22,8,17,6,25,11)、FCFS(0-29)、FoLi(0,2,3,4,5,8,9,12,19,20,21,28,29,1,6,7,10,11,13,14,15,16,17,18,22,23,24,25,26,27)。经计算,FCFS方法所得调度序列的总船舶调度时间最优解为6 813.8 min,单船最大调度时间238.8 min；FoLi方法所得调度序列的船舶总调度时间最优解为6 353.0 min,单船最大调度时间为382.4 min,通过比较,SK-NSGA-II下总船舶调度时间最优解较FCFS及FoLi方法分别下降33.5%和28.7%,因此无论是总船舶调度时间还是单船最大调度时间,SK-NSGA-II求解出的优化方案均有较大提升。

(3) 模型有效性验证。对模型有效性验证主要分析其求解出的最优船舶交通组织方案(表3为前10条船舶信息)是否满足模型约束条件要求。单向/混合通航模式转化验证,12号出港船载重吨大于5万吨,被安排为单向通航,下一艘21号出港船载重吨小于5万吨,被安排为混合通航模式,此时单向通航转化为混合通航模式,两船在航道关键点4保持了预设的至少8 min港池同向安全时隙。21号出港船和7号进港船载重吨小于5万吨,均被安排为混合通航模式,下一艘15号进港船载重吨大于5万吨,被安排为单向通航,此时混合通航转化为单向通航,且15号船与21号和7号船在关键航路风险点1位置保持了预设的至少8 min港池异向安全时隙。最后,经验证其他船的通航模式转换约束也均得到保证。其他模型约束验证：21号出港和7号进港船载重吨小于5万吨,均被安排为混合通航模式,且两船开始被调度时间均晚于其完全就绪时间,同时两船在关键点2、5分别保持了至少30 min、20 min的安全时隙,从而保证了两异向混合通航船在驶入混合航道单向子航道(Key 1和Key 3之间)后的整个航行过程只能保持单向通航,且避免了两异向船在港池连水域(Key 4和Key 6之间)的会遇冲突。15号和27号进港船载重吨大于5万吨,均被安排单向通航,两船开始被调度时间均晚于其完全就绪时间,且两船各自被调度总时间等于其在航道各关键点和港池航行时间的总和,同时两船在航道关键点1-6位置保持了至少8 min同向安全时隙,从而保证船舶在航行过程中的时间安全性和连续性。最后,经验证其他模型约束也均得到保证。

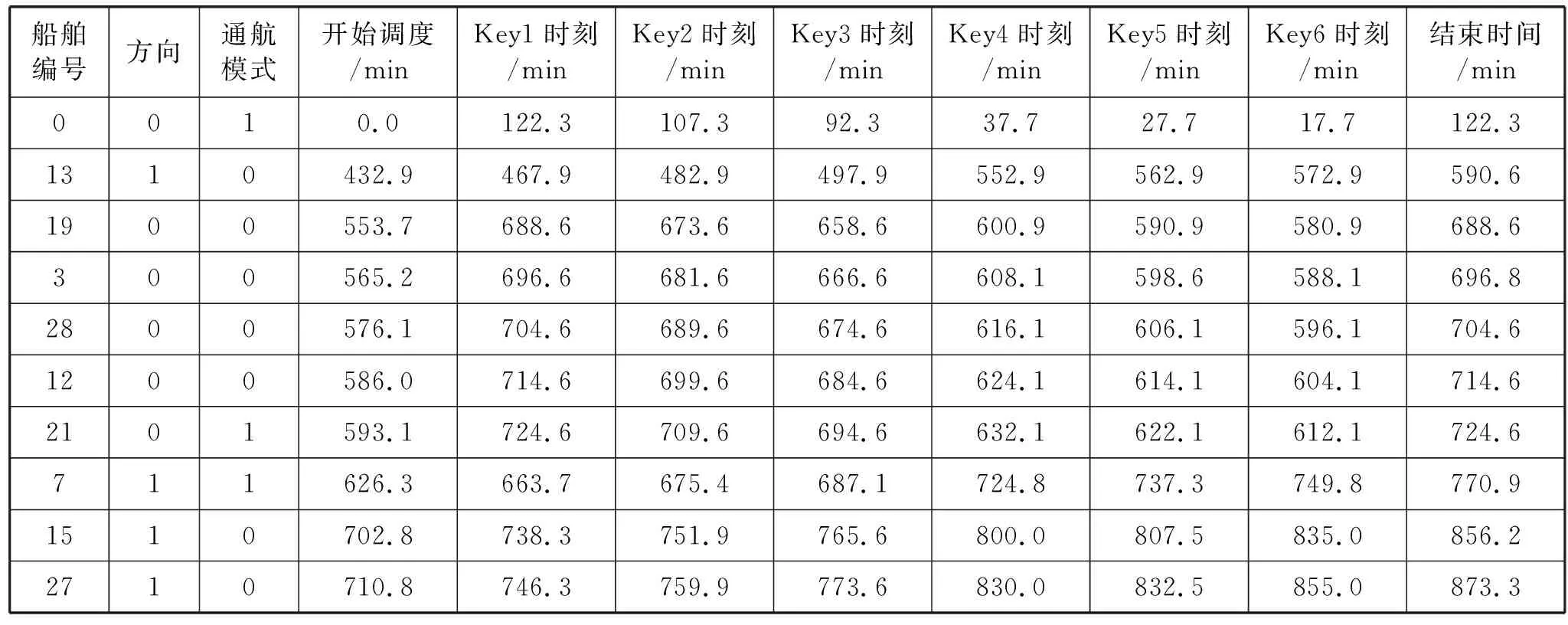
表3 船舶交通组织方案

4 结 语

本文针对国内外港口混合类型航道特点,抽象出一种串行式简单混合类型航道作为研究对象,构建了以单向/混合通航模式转化、混合航道异类子航道间通航模式切换、港池连接水域船舶交通冲突消解等为约束的串行式混合类型航道船舶交通组织优化模型。提出一种Spark分布式多目标遗传算法,将全部种群分散在了多节点上并行执行算法的遗传操作,快速高效地求取出了船舶进出港优化方案。实验结果表明提出的串行式简单混合类型航道船舶交通组织优化方法合理、有效,能够保证船舶安全航行的前提下有效提高船舶进出港作业效率。然而实际混合类型航道常因港口自然地理等条件限制而具有多样性和特殊性等特点,本文主要针对一种串行式简单混合航道类型进行初步理论研究,相应成果可为下一步构建更贴近实际的复杂混合类型航道船舶交通组织优化模型奠定基础。