基于随机模型预测控制的四旋翼无人机研究

李姗姗 龚 薇

(四川大学电气信息学院 四川 成都 610065)

0 引 言

近年来，由于科学技术的加速发展，无人驾驶飞行器的应用越来越广泛，如搜索救援任务[1-2]、火灾监测[3]、边境巡逻[4]、作物监测[5]和基础设施检查[6-8]等。而四旋翼飞行器凭借其具有悬浮、高机动性和简单设计的特性，成为最常用的飞行器之一。然而，尽管它们具有巨大的应用潜力和操作自主性，但从技术演示到实际应用的转变却是一个缓慢的过程。造成这一重大差距的原因在于无人机飞行器实际操作中通常会受到干扰的影响，为了保证飞行可行性，如何处理干扰是无人机飞行器的首要考虑之一，也是目前的重大挑战之一。

在过去的几十年中，已经发表了许多关于四旋翼动态建模的文章[9-11]。Mistler等[12]首次将反馈线性化方法应用于四旋翼飞行跟踪参考轨迹。Bouabdallah等[13]比较了两种基于模型的直升机稳定性控制技术的性能:一种采用简化动力学的经典PID方法和一种基于更完整模型的现代LQR技术。Castillo等[14-15]给定四旋翼的位置，并应用嵌套饱和控制来稳定其姿态。Xu等[16]提出了一种滑模控制器来稳定一类级联欠驱动系统。另一种常见的控制方法是逆步进技术[17]。

然而近几年计算机计算能力的增强，使得先进的控制器成为可能。在这种情况下出现的一个突出的控制策略是模型预测控制(MPC)。回溯到20世纪70年代末，模型预测控制在最初的构想是控制化学工业过程[18]，它通常具有缓慢的动力学和以秒或分钟计算的采样时间。由于当今的高性能处理器，MPC已经被应用于四旋翼飞行器中的快速系统。2013年Subbarao等[19]根据一个四旋翼的线性化模型建立了一个MPC模型。建立的控制器可以跟随轨迹，同时能处理对飞机方向施加的限制(滚轴和俯仰角)。但这种方法无法处理系统中存在的不确定扰动，一种常用的处理扰动的方法为鲁棒模型预测控制，但这种方法可能由于过度保守而无法解出可行解。一种自然而然的想法便是放宽约束，使约束在一定概率内满足，这种考虑导致了随机模型预测控制(SMPC)的出现，该方法可以使系统在满足约束与控制性能之间进行权衡，这导致系统控制性不再那么保守。

实际上，在无人机飞行中，可以找到多个扰动源，如位置或速度测量误差、电机速度失调，甚至大气阻力，以及一些未知分布的随机扰动。本文在只知道扰动一阶矩及二阶矩的情况下，提出一种SMPC控制方案，实现在一定程度上满足约束。扰动的处理采用分布式鲁棒方法求出其模糊集，再针对软化后的单输入约束与联合状态约束进行分别处理。前者采用最坏情况下的条件风险值约束进行等价转换，然后运用定理等价为可计算的半定规划(SDP)凸优化约束。后者采用布尔不等式将联合约束转换为多个单状态约束，再运用凯特利切比雪夫不等式将非凸约束转换为凸约束。计算过程中采用了在线扰动反馈，该方法可解决状态反馈存在的非凸问题。针对该算法，本文在末尾进行了凸优化可计算分析以及可行性稳定性分析，证实了该算法的可计算性、可行性与稳定性。

1 四旋翼无人机的模型和问题描述

1.1 四旋翼无人机的线性模型

在本节中，我们通过转换地面坐标系原点与机体坐标系原点对四旋翼无人机建立力学研究坐标系(如图1所示)，并建立了四旋翼无人机的六自由度动力学模型，将其应用于控制器的设计中。基于结构建立的模型可以显著提高设计和测试效率，对控制系统的设计和性能分析具有重要的意义。

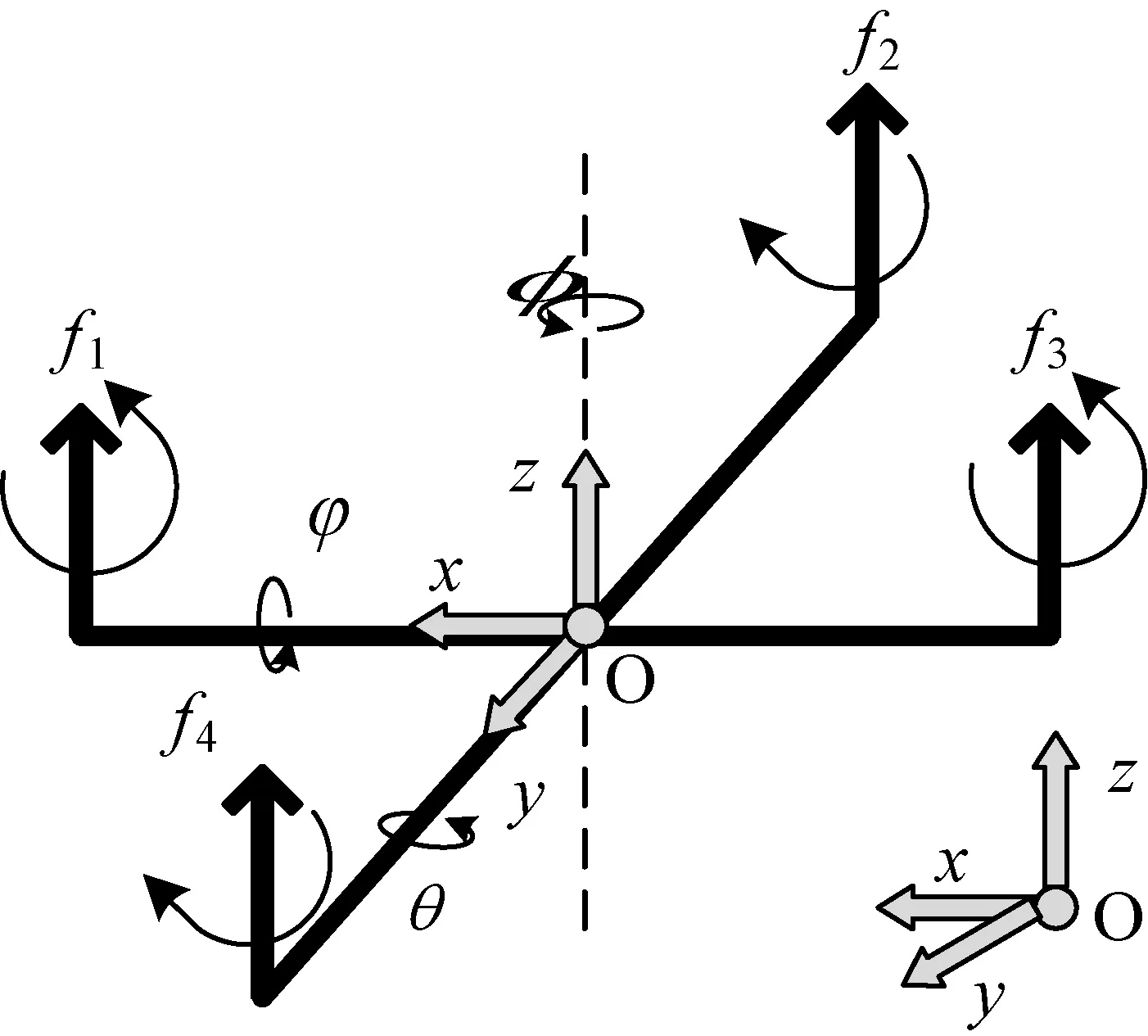
图1 四旋翼无人机坐标系统

通常，四旋翼无人机被建模为一个具有6个自由度[x,y,z,φ,θ,φ]的刚体，其中：x、y、z分别表示笛卡尔坐标系中的状态；φ、θ、φ分别表示俯仰角、旋转角与偏航角。

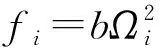
式中：b和d分别表示推力系数和阻力系数。则其非线性动力学模型可以由欧拉-拉格朗日方程[13-14]推导得。

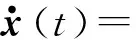
假设无人机在近似悬停状态时，该动力学模型可以由一个线性的模型来近似，在工作平衡点附近使用一阶泰勒展开[20]，最终转化成线性离散状态空间模型为:

(1)

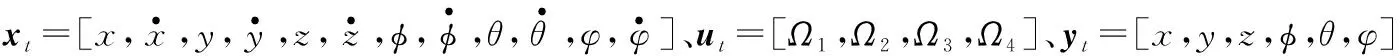
1.2 约束条件

如上所述，四旋翼无人机的动力学模型有6个输出[x,y,z,φ,θ,φ]，四个独立的输入[Ω1,Ω2,Ω3,Ω4]。由于四旋翼的欠驱动性质，在[x,y,z,φ]达到理想位置时，只需[φ,θ]保持稳定[21]。因此需要限制它们的振幅。这些约束能被表示为:

φmin≤φ≤φmax

θmin<θ≤θmax

这些约束可由线性不等式约束集合定义的凸区域Fx定义为如下形式：

(2)

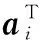
在实际飞行中，马达转速也会受到电压的限制，则控制输入受到约束，可表示为:

u≤umax

同理，控制输入可表示为如下线性不等式描述的凸可行区域Fu:

Fu={u|Hu≤h}

(3)

其中，系数H与h定义如下：

2 模型预测控制算法的重构

2.1 模型预测控制的系统模型

在有限时间的最优控制中，假设模型是从t到t+N求解优化问题，其中N为预测视界。定义状态、输入、扰动与输出的紧凑模式如下：

(4)

则式(1)可转换为如下紧凑形式：

(5)

式中：C∈RNq×Nn，主对角线值为C，除主对角线外均为0；A、B、D和G可参考文献[22]，文献中展示了详细推导过程。

同理，由定义(4)可将式(2)与式(3)转换为如下紧凑模式:

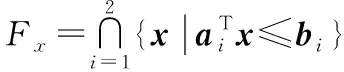
式中：ai∈R(N+1)q，bj∈R，H∈RNu×Nm,h∈RNm。由于扰动的分布未知且无界，不能保证约束总是能得到满足，因此可允许一定概率违反约束。在这种情况下，通过考虑系统中存在不确定性的所有可能性，可在系统性能与约束满足之间进行权衡。将Fx与Fu替换为如下概率约束：

P(x∈Fx)≥1-δx

(6)

P(u∈Fu)≥1-δu

(7)

式中：δu∈(0,1)、δx∈(0，1)分别表示输入与输出最大的违反概率。对于线性问题，常定义如下二次函数为目标函数：

(8)

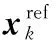
(A+BK)TQN(A+BK)-QN+Q+KTRK=0

故重构后的四旋翼无人机的目标跟踪问题P1如下：

minVN(xt,u,w)

(9)

s.t.x=Axt+Bu+DGw

y=Cx

P(x∈Fx)≥1-δx

P(u∈Fu)≥1-δu

2.2 扰动反馈重构

由于控制输入u应该是具有当前和过去状态的某种反馈控制策略，故常采用反馈结构定义控制策略u。以往反馈形式常采用状态反馈参数化，但预测的输入序列和状态序列是状态反馈增益序列的非线性函数，故一般情况下，可行决策变量集是非凸的。另一种可计算的凸优化反馈控制策略为放射扰动反馈参数化[24]。

(10)

式中：Mi,j∈Rm×n，vi∈Rm。在相关文献中，这种扰动反馈控制策略被证明与状态反馈控制策略是等价的[24]。同理，式(10)可以表示为如下紧凑形式：

u=MGw+v

式中：M∈RNm×Nn，v∈RNm，其具体形式与推导过程可参考文献[24]。将反馈结构加入P1，可转换为如下P2问题:

minVN(xt,u,w)

s.t.P(HMGw+Hv-h≤0)≥1-δu

1-δx

3 约束的重构

3.1 扰动的重构

式中：E[P][·]表示在分布下P的期望，μ=1N⊗μ0，Σ=IN⊗Σ0，μ0为扰动均值，Σ0为扰动方差,⊗表示克罗内克积，分别定义为E[ωi]=μ0，Σ[ωt]=Σ0且均已知。

在分布P未知的情况下，通常式(7)的可行集为非凸的，有时甚至是不连通的。对概率分布中不确定性处理的一种常见方法是采用分布鲁棒方法[25]，定义分布鲁棒的输入机会约束与联合状态约束如下：

处理后的输入与状态约束再分别采用合适的方法进行精确凸重构。

3.2 输入约束的凸重构

众所周知，鲁棒的单机会约束可以被最坏情况下的条件风险值约束保守地近似，且在文献[25]推理2.1中，证明了当原硬约束为扰动的仿射函数时，该近似是等价的。故上述单输入约束可等价为如下最坏情况下的条件风险值约束：

P-CVaRδu(Hv-h+HMGw)=

式中：P-CVaRδu(a)为δu概率下满足条件a的概率。并且根据文献[25]，可将单输入最坏情况下的条件风险值约束等价为如下可计算的SDP约束：

其中：trace(a)为求矩阵a的迹；N为优化的变量。

SDP模型在计算时通常比较复杂。SOCP模型是SDP模型的特例，但变量更少，算法效率更高，故将上述SDP约束转换为如下SOCP约束的形式，提高计算效率[26]：

(11)

3.3 联合状态约束的随机模型预测控制重构

由于联合状态约束需要在不确定性分布上求解多元积分，导致其求解过程十分棘手，且通常为非凸约束。为了得到一个近似可处理形式，常采用布尔不等式进行转换。首先，需要将状态鲁棒机会转换为上确界形式。

再应用布尔不等式得到如下转换：

式中:δxx=δx/l为输出最大违反概率δx的l次均值分配，这种固定风险分配可避免优化算法的非凸性。转换后的分布式鲁棒联合状态约束可转换为如下形式的保守逼近：

(12)

运用坎特利凯特利切比雪夫不等式，可将式(12)固定风险分配后的状态约束转换为如下可计算的凸优化形式，近似文献[27]引理4.1。

在本文中，由P2可知l=2。单输入约束与联合状态约束经过一系列转换，均近似成可处理的凸约束。重构后的P2问题可以转换为如下的P3问题：

minVN(xt,u,w)

(13)

4 系统性能分析

4.1 系统的可计算分析

显然，在P4问题中，目标函数与单输入约束都是凸的线性约束，但联合输出约束中，由于Σ[x]的存在，使得状态约束在CVX包中不可计算，故将其进行如下转换：

ζi=BMGΣGTMTBT+DGΣGTDT+

BMGΣGTDT+DGΣTGTMTBT

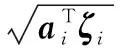
此外，为了保证在任意状态输入的情况下，均存在可行解，可在目标函数中引入了松弛变量，结合式(11)与式(12),P3问题可以转换为如下P4问题：

mint

s.t.VN(xt,M,v,w)≤t

4.2 可行性与稳定性

因为无界扰动的存在，使状态保持在硬约束系统的可行域中是不切实际的。本文通过软化约束以及加入松弛变量等方法解决了该问题。只有当违反约束时，松弛变量才是非零的，其余情况松弛变量则保持为零。这种精确罚函数方法可以使软化约束的解集与原硬约束的解集等价，即针对一个初始状态，原硬约束问题不可行时，新构建的软约束问题却可以产生一个可行的终端解集，且该解集与原硬约束问题可行时解出的解集是相同的，而这种思想保证了系统的可行性。

当矩阵A为舒尔稳定时，文献[27]已证明其稳定性，接下来我们证明当A为李雅普诺夫稳定时系统的稳定性。

系统李雅普诺夫稳定时，存在一个坐标变化，使系统分解为如下形式：

式中:A1为舒尔稳定部分，A2特征根在单位圆上，具有相同的代数和几何多重性。假设A2为对矩阵角，且主对角线上元素要么为±1，要么为2×2的旋转矩阵，因此A2为正交矩阵。

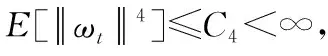
对于任意ε>0，考虑如下“负漂移条件”：

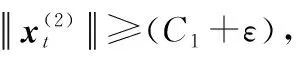
此外，不难得到以下关系成立：

由于控制与扰动的一阶矩均有界，故存在常数M满足:

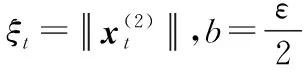
5 仿 真

在本节中，为测试几种控制策略对轨迹跟踪问题的性能，进行了如下数值模拟。仿真中使用的模型参数如表1所示。

表1 四旋翼无人机的参数

无人机到达目标点的顺序参考如下：

(0,0,0)→(0,0,5)→(5,0,5)→(5,10,5)→

(-5,10,5)→(-5,0,5)→(5,0,10)

考虑初始状态为[x,y,z]=[0,0,0]，角度状态为[φ,θ,φ]=[0,0,0]，采样时间τs=50 ms,惩罚权重Q=10I12，R=0.01I4。为了加强飞行的稳定性，分别对姿态和输入进行了约束，姿态约束为：φmin=-0.5,φmax=0.5,θmin=-0.5,θmax=0.5输入约束为：umax=[250,250,250,250]，则仿真结果如图2-图4所示。

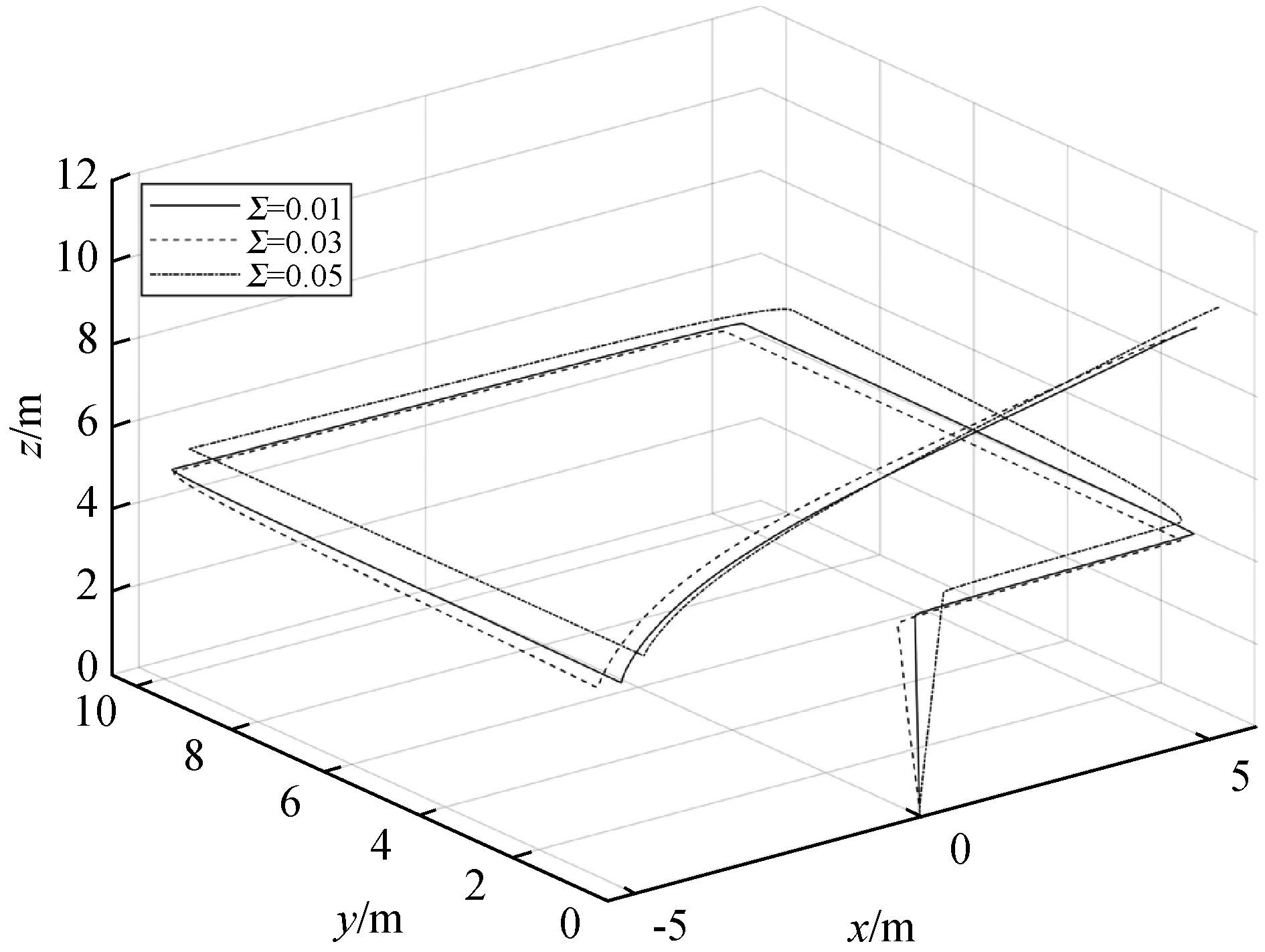
图2 无人机在不同扰动下的位置变化

图3 无人机在不同扰动下θ的稳定情况

图4 无人机在不同扰动下Φ的稳定情况

由图2可以看出，在不同扰动相同步数的情况下，系统仍然可以实时有效跟踪，但随着扰动的增大，距离规定点的误差越大。图3-图4显示不同扰动下俯仰角Φ与旋转角θ均可保持稳定。

图5-图8展示了MPC[21]与SMPC性能对比。图5显示在相同步数的情况下，SMPC不仅能克服随机扰动，而且在反馈的作用下反应速度更快，比无扰动的MPC更快到达每一步的终点。图6-图8显示SMPC算法能够在满足系统约束的情况下克服随机扰动实现目标跟踪，且消耗燃料与无约束的MPC算法相差无几。

图5 两种算法下的位置变化

(a) MPC

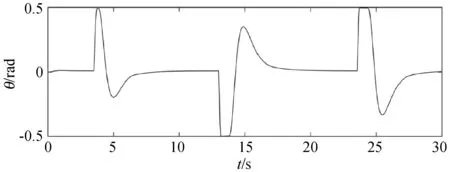
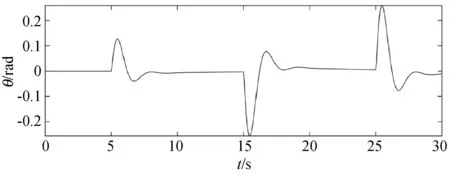
(b) SMPC图6 两种算法下θ的稳定情况

(a) MPC

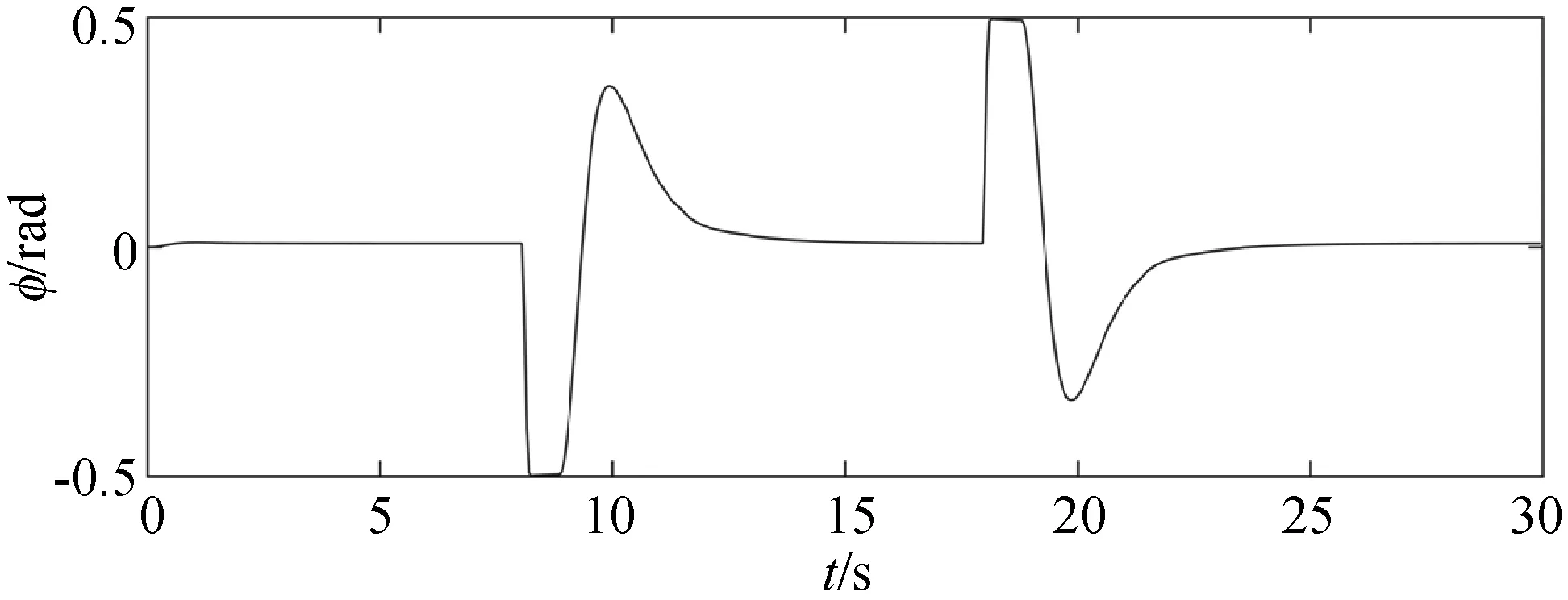
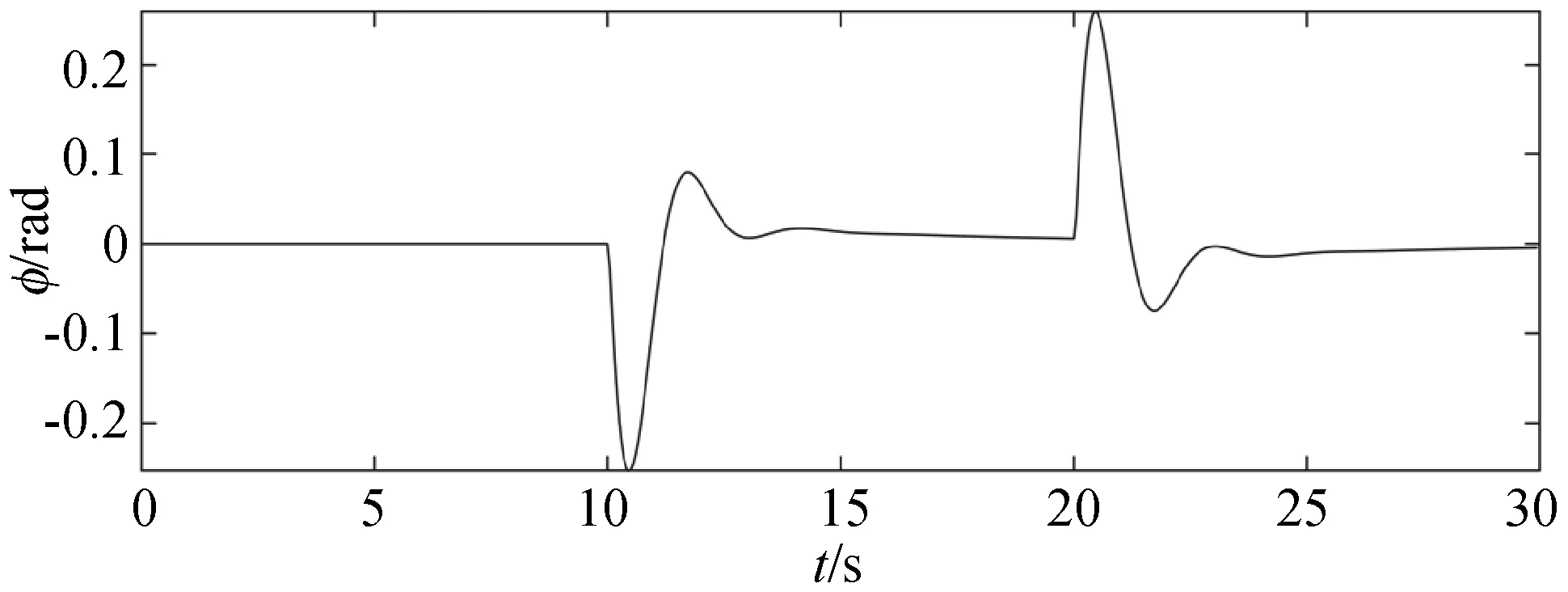
(b) SMPC图7 两种算法下Φ的稳定情况

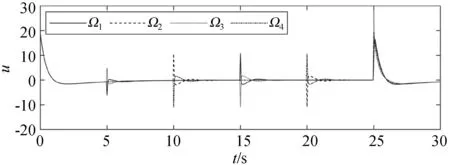
(a) MPC

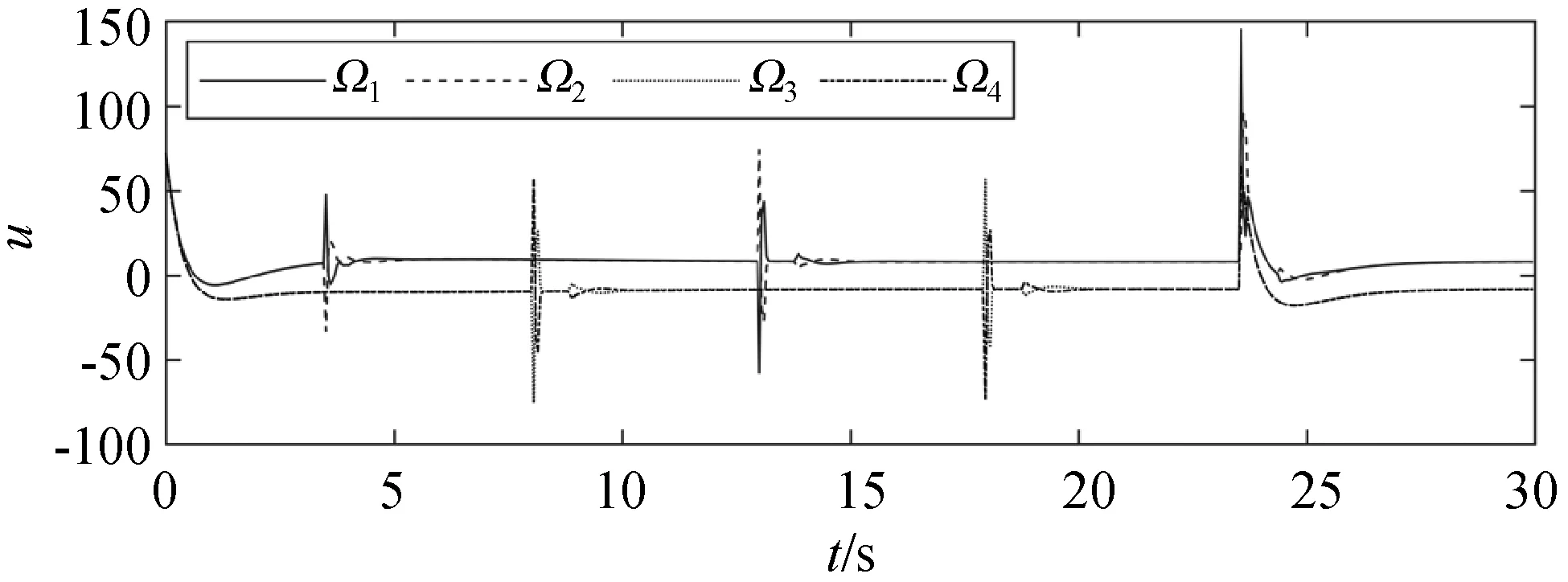
(b) SMPC图8 两种算法下的输入

图9展示了不同预测步数对SMPC算法的影响，可以看出，当增大SMPC的预测步数时，相应速度也可以增加得更快，稳定性也会更好。图10展示了不同输入对SMPC算法的影响，可以看出，当初始状态不同时，系统均可解出优化解完成路径跟踪。

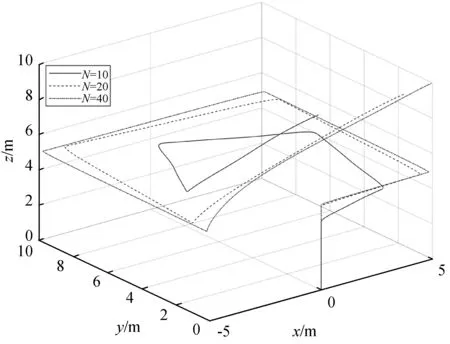
图9 不同预测步数下的位置变化

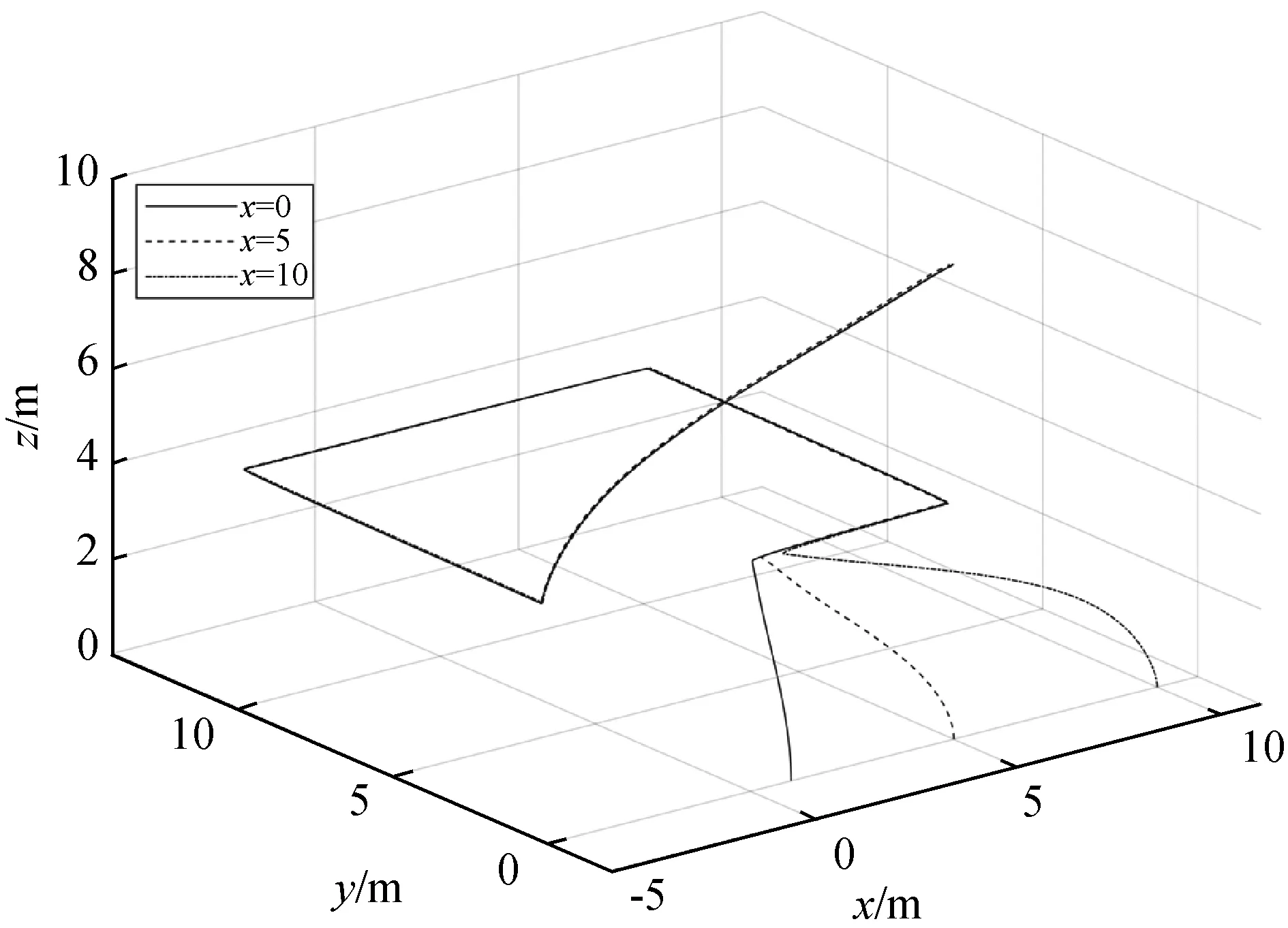
图10 不同初始状态下的位置变化

6 结 语

针对四旋翼直升机的稳定性和航迹跟踪问题，本文提出一种随机模型预测控制器。在利用随机模型预测技术进行四旋翼无人机控制的相关工作中，该方案的主要优点在于：1) 具有处理系统不确定性扰动的能力；2) 考虑扰动反馈下的输入约束与联合状态约束；3) 运用近似等价的方法对软输入约束与联合状态约束进行凸重构；4) 运用机会约束与松弛变量保证了系统在不同初始状态下均有解集，且与原硬输入解集相同。在仿真实验中，我们将SMPC的性能与MPC方法进行了比较，结果显示本文方法能够更好地处理扰动且具备更优秀的预测性能。