基于组合形态学的齿轮参数视觉测量方法
朱 浪 方成刚 粟序明
(南京工业大学机械与动力工程学院 江苏 南京 210000)
0 引 言
齿轮精度是齿轮产品质量的重要衡量指标,在齿轮的批量生产中,齿轮在线测量对保证加工质量和提高生产效率具有重要意义。齿轮测量有接触式测量和非接触式测量之分[1],视觉测量技术具备在线实时非接触测量、自动分析等功能,得到了快速发展和应用[2]。
随着机器视觉测量技术水平的快速提高,齿轮视觉测量技术的研究得到了深入开展。Gadelmawla等[3]建立了机器视觉齿轮几何参数测量系统,实现对直齿圆柱齿轮多项参数的非接触测量,但系统测量误差只达到±0.101 mm。王宁等[4-5]研究小模数齿轮的各单项偏差视觉测量方法,具有较高测量精度,但所用测量平台只能获取齿轮部分图像,无法对齿轮几何参数进行测量。饶艳桃[6]研究实现了渐开线标准直齿圆柱齿轮结构参数的测量,但对齿轮边缘检测算法没有深入研究,测量精度有限。从各学者对齿轮视觉测量的研究中可以看出,图像边缘检测技术是齿轮视觉测量的关键技术之一,其检测结果将会直接影响到齿轮参数测量的准确度和精度。
图像边缘被定义为图像中像素灰度值不连续或者像素灰度值急剧变化的像素点集,图像边缘检测技术是用于识别图像边缘的数学方法[7]。经典的边缘检测算子有Roberts算子、Sobel算子、Prewitt算子、Laplace算子和Canny算子等[8],它们都是基于微分的边缘检测算法,容易受噪声影响产生伪边缘和不连续现象,不能满足齿轮实时高精度测量的要求。近年来,涌现出一些新的边缘检测方法,如基于小波变换[9]、基于数学形态学变换[10-11]、基于群智能仿生优化算法的边缘检测方法[12],其中基于数学形态学的边缘检测算法简单且具有较高的边缘检测精度和良好的抗噪性,在一定程度上提高了边缘检测的精度。
为实现齿轮参数实时高精度检测,提出一种基于组合形态学的齿轮参数测量方法,采用检测精度高、抗噪声性强且算法简单的组合形态学边缘检测算子有效地提取齿轮单像素边缘,从而实现对齿轮各几何参数的快速高精度测量。
1 齿轮视觉测量平台
1.1 视觉测量平台硬件选型
搭建的齿轮视觉测量平台如图1所示,采用维视千兆网连接的500万像素的CMOS的工业相机,搭配12 mm焦距的AFT相机镜头光源选用维视LED面板背光源来突出齿轮轮廓对比度,计算机用于采集齿轮图像及后期图像处理,采集的齿轮图像如图2所示。

图1 齿轮视觉测量平台

图2 原始齿轮图像
1.2 相机标定与图像畸变矫正
1.2.1相机成像模型
相机的成像模型如图3所示,假设点PW(x,y,z)是物平面内的某一点,在相机坐标系下对应点Pc(x,y,z),在图像坐标系下对应点Pd(x,y),在像素坐标系下对应点Pu(x,y)。
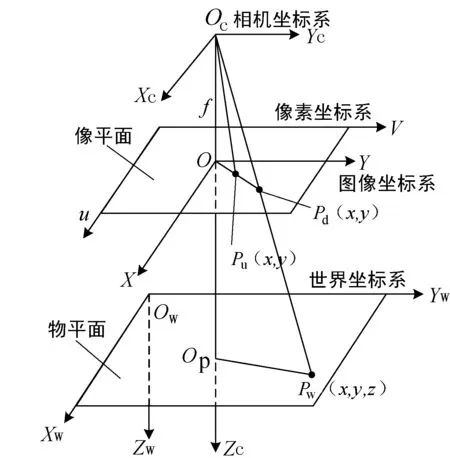
图3 相机成像模型图
根据透射投影的成像原理,相机理想成像的最终数学模型如下:
(1)
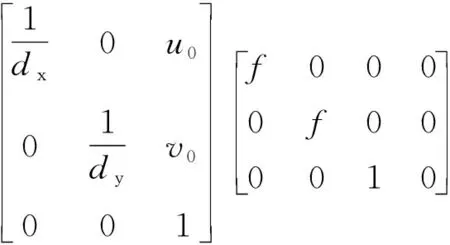
1.2.2成像畸变数学模型
由于采用的相机镜头为球面透镜以及安装误差的存在,会产生径向畸变和切向畸变,从而影响测量系统的测量精度,故须对采集的图像进行畸变矫正。
(1) 径向畸变数学模型如下:
(2)
(2) 切向畸变数学模型如下:
(3)
式中:r2=x2+y2;共有5个畸变参数,k1、k2、k3为径向畸变系数,p1、p2为切向畸变系数。
采用Zhang[13]的黑白棋盘格标定方法,其中,标定板采用9×9的棋盘格标定板,其方格尺寸为4 mm,采集不同位姿、不同角度的20幅标定板图片存放在同一文件夹下,利用MATLAB R2018a 的Camera Calibration APP 加载标定板图像对相机进行标定,获得相机参数[14],主要参数如表1所示,可看出,相机径向畸变对误差的影响远大于切向畸变。
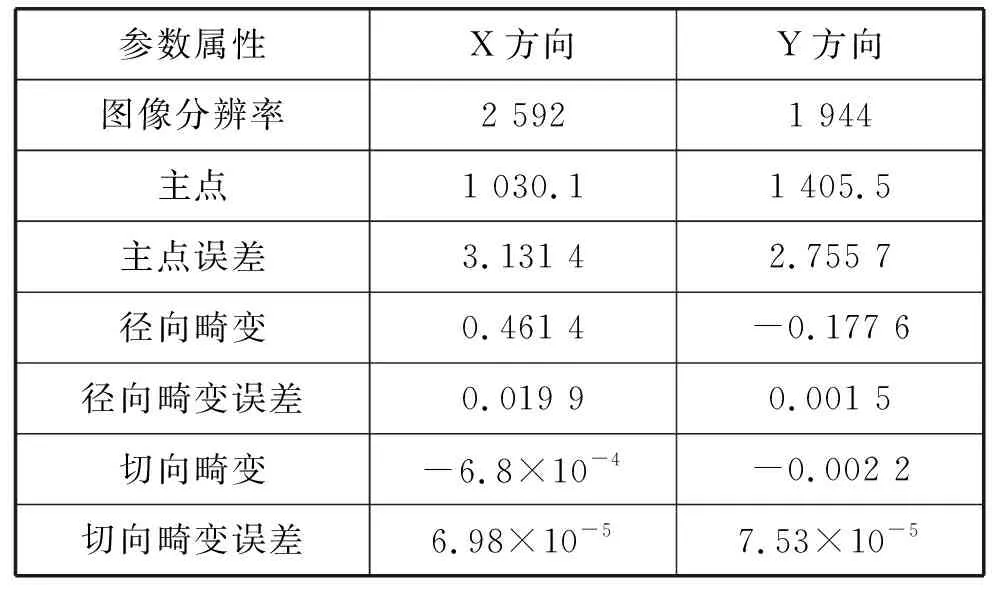
表1 相机主要参数
相机标定获得内外参数后,即得到了相机的畸变参数,最后根据相机成像畸变数学模型计算出矫正后的图像坐标,畸变矫正后的图像如图4所示。

图4 畸变矫正后齿轮图像
2 齿轮图像处理
2.1 图像预处理
对畸变矫正后的图像进行预处理,工业相机采集的图像是灰度图像,所以不需要进行灰度处理,只需对图像滤波去噪后进行二值化处理。
由于齿轮测量需要获取齿轮轮廓信息,而中值滤波在去噪的同时能很好地保留边缘信息,所以采用中值滤波算法对矫正的原始图像进行滤波操作[15],滤波结果如图5所示。其次,为降低图像边缘检测的计算量,对图像进行二值化处理,采用最大类间方差法(OTSU)法自动确定阈值对齿轮图像二值化[16],齿轮图像二值化后如图6所示。

图5 自适应中值滤波 图6 齿轮图像二值化
2.2 键槽轴孔填充
测量的齿轮是一个带键槽轴孔的齿轮,不利于齿轮圆心的精确定位,故将齿轮键槽轴孔填充获得完整无孔洞的齿轮图像。
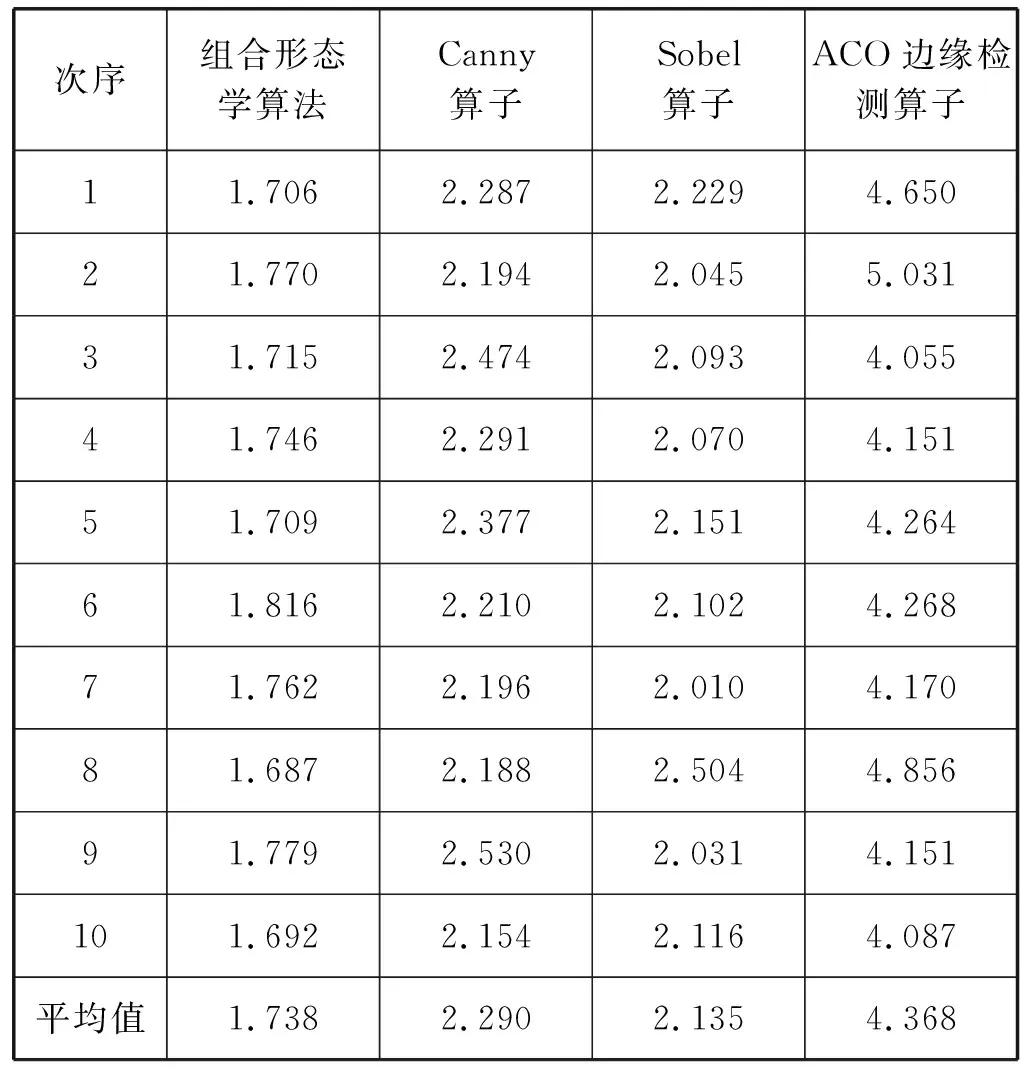
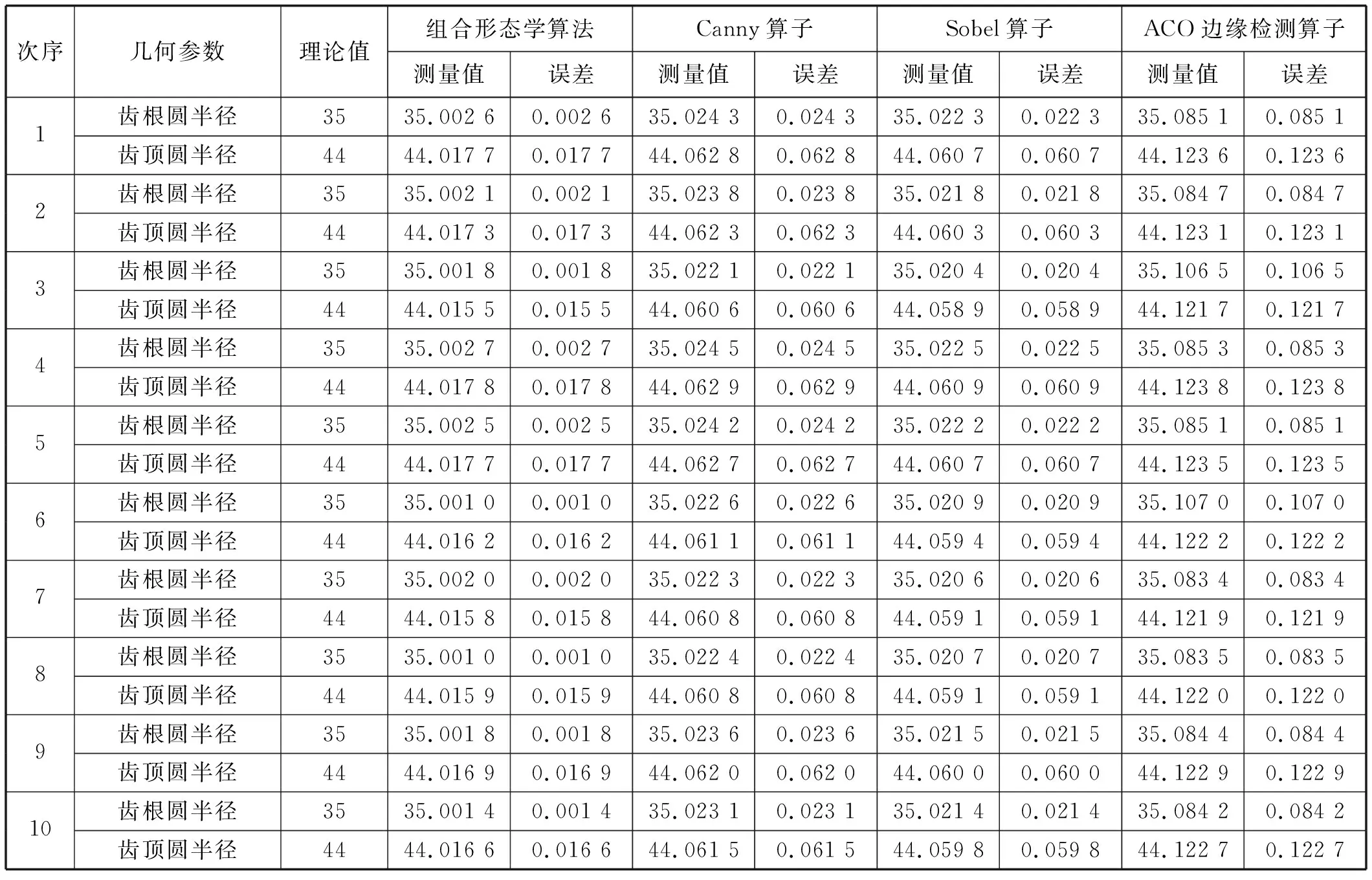
采用连通域分析法删除二值图像中的小连通域。首先计算二值图像中的每个连通区域L(i),其次计算每个连通区域像素的个数,即每个连通区域的面积Area(i),最后设置阈值P,当Area(i) 本文处理的齿轮二值图像前景为黑色(像素值为0),背景为白色(像素值为1),背景共有齿轮外部和齿轮内部轴孔两个连通区域,设齿轮外部连通区域面积为Area(1),齿轮内部轴孔连通域面积为Area(2),令P=Area(1),显然Area(2) 图7 齿轮键槽轴孔填充图像 数学形态学(Mathematical Morphology),是基于积分几何和几何概率理论建立的关于图像形状和尺寸的研究方法,其实质是一种非线性滤波方法。 2.3.1形态学基本运算 基本的形态学变换操作是膨胀(Dilation)、腐蚀(Erosion)以及建立在这两种运算基础之上的开(Open)运算和闭(Close)运算。 膨胀和腐蚀实质上都是一种卷积操作,卷积范围是结构元素大小对应的像素集,设原始图像为f(x,y),结构元素为s(m,n)。其中,Df是图像f(x,y)的定义域,Ds是结构元素s(m,n)的定义域。 (1) 膨胀运算是将当前像素值替换成结构元素对应的像素集中的最大像素值,定义如下: (f⨁s)(x,y)= (4) 膨胀运算可以填充孔洞,增强边缘的连续性。 (2) 腐蚀运算是将当前像素值替换成结构元素对应的像素集中的最小像素值,定义如下: (f⊖s)(x,y)= (5) 腐蚀运算可以去除图像中的噪点,细化边缘。 (3) 开运算是先将图像进行腐蚀操作,再对腐蚀后的图像进行膨胀操作,定义如下: f∘s=(f⊖s) ⨁s (6) (4) 闭运算是先将图像进行膨胀操作,再对膨胀后的图像进行腐蚀操作,定义如下: f·s=(f⨁s) ⊖s (7) 开运算和闭运算可以去除图像中的离散点和细小空洞,同时起到平滑边缘的作用。 2.3.2形态学边缘检测 形态学边缘检测的基本思想是不同灰度值的相邻区域经过形态学变换后,边缘灰度值的变化程度比图像中非边缘部分要明显[17]。以下是三中常用的形态学梯度边缘检测算子。 (1) 膨胀型梯度算子: G1(f)=(f⨁s)-f (8) (2) 腐蚀型梯度算子: G2(f)=f-(f⊖s); (9) (3) 膨胀腐蚀型梯度算子: G3(f)=(f⨁s)-(f⊖s) (10) 膨胀型梯度算子由于需要先进行膨胀操作,会扩大噪点且提取的边缘较粗,适合处理边缘完整性较差的图像;腐蚀型梯度算子提取边缘较细,且能有效抑制噪声。 本文采用的边缘检测算法结合了形态学开运算与腐蚀型梯度边缘检测算子,算法过程如下: ① 对预处理后的二值图先采用形态学开运算,去除离散噪声点的同时平滑二值图像边缘,执行式(6)。 ② 再利用腐蚀型梯度算子提取齿轮图像的单像素边缘,执行式(9)。 图8为本文采用的组合形态学边缘检测算法提取的齿轮边缘图像,准确定位到齿轮单像素边缘。 图8 组合形态学边缘检测的齿轮边缘图像 为了验证本文组合形态学边缘检测算法的抗噪性,对齿轮原图像加入一定密度的椒盐噪声,然后与传统的一阶边缘检测算子Sobel、二阶算子Canny以及群智能算法中的蚁群算法边缘检测算子(ACO)作对比,分别用它们检测含有噪声的齿轮图像,结果如图9所示。可以看出,其他三种边缘检测算子对噪声敏感,不能有效检测出齿轮的边缘,而本文所提出的组合形态学边缘检测算法具有更好的抗噪性,能够准确定位到齿轮图像的单像素边缘。 (a) 齿轮原图 (b) 加入椒盐噪声的齿轮图像 (c) Sobel算子 (d) ACO边缘检测算子 (e) Canny算子 (f) 本文组合形态学边缘检测算法图9 含椒盐噪声的边缘检测对比 基于组合形态学的齿轮参数视觉测量方法的流程如图10所示。 图10 齿轮参数视觉测量方法流程 齿轮圆心是齿轮几何参数测量的基准,采用重心法定位齿轮圆心。将处理好的完整无孔洞的齿轮二值化图像进行黑白反转操作,对反转后的图像按行和列遍历,遍历到齿轮部分的连通域时,记录像素点对应的横纵坐标,将齿轮部分像素点的横坐标累加在集合x(i)中,将齿轮部分像素点的纵坐标累加在集合y(i)中,分别求横纵坐标集合的均值得齿轮圆心坐标(X0,Y0),图像中齿轮部分的重心法定位齿轮圆心点的定义如下,其中i=1,2,…,N。 (11) 图11为定位到的齿轮圆心。 图11 齿轮圆心定位 采用组合形态学边缘检测算法得到齿轮边缘点坐标(xi,yi),按下式计算齿轮每个边缘点到齿轮圆心坐标(X0,Y0)的距离d(i),其中i=1,2,…,N。 (12) 将距离d(i)从d(i)min到d(i)max按区间t来统计属于该距离区间的d(i)的数量num,并绘制num-d柱状图,如图12所示,其中,区间t的取值决定测量精度。 图12 齿轮边缘点到圆心距离数量统计 图12中最高的两个柱形对应横坐标的距离值分别为齿根圆半径Rf和齿顶圆半径Ra。 采用连通域计数法统计齿轮的齿数,先以(Ra+Rf)/2为半径生成一个圆形掩膜,再将掩膜模板与齿轮二值图像相乘,得到前景只含有轮齿的图像如图13所示,最后计数连通区域数量得到齿轮的齿数Z。 图13 掩模处理后的轮齿图像 根据已经测量得到的齿顶圆半径Ra和齿根圆半径Rf,按如下公式计算所测量的齿轮模数: (13) 齿轮模数m是标准值,将式(13)计算结果对照国家标准模数系列表(GB/T 1357—2008),查找到与其差值最小的标准模数值即为所测齿轮模数m。计算公式如下: m差=|m计-m标| (14) 式中:m计是按式(9)计算得到的模数值,m标是模数系列表(GB/T 1357—2008)中的标准模数值,当m差取得最小时对应的m标即为所测齿轮的模数m。 本文齿轮参数视觉测量系统的测量对象为一标准的渐开线圆柱齿轮,其理论参数如表2所示,在搭建的视觉测量平台上进行实验,结合MATLAB R2018a编程进行图像处理来测量齿轮的基本几何参数。 表2 齿轮理论参数表 在与齿轮视觉测量视场相同的情况下采集长度L=20 mm的标准量块图像,对采集的量块图像畸变矫正后进行边缘检测,利用hough变换拟合量块边缘直线,计算得到量块对应的像素长度D=429.276 pixel,设像素当量转换系数为k,像素当量标定结果如下: (15) 为验证提出的组合形态学边缘检测算法测量精度更高,速度更快,进行了10次连续测量实验,并与Canny算子,Sobel算子,蚁群边缘检测算法(ACO)进行了对比,其中,每次实验测量得到的齿数Z和模数m都与理论值相同,不存在误差,故只对齿根圆半径Rf、齿顶圆半径Ra的测量结果进行列表对比来验证组合形态学边缘检测算法的优势。边缘检测算法测量耗时对比结果如表3所示,边缘检测算法测量误差对比结果如表4所示。 表3 边缘检测算法测量耗时对比 单位:s 表4 边缘检测算法测量误差对比 单位:mm 从表3对比结果可以看出,组合形态学边缘检测算子的运行速度更快;从表4对比结果可以看出,基于组合形态学边缘检测算法的齿轮参数测量方法与其他几种边缘检测方法相比,测量精度更高,达到17.8 μm;重复性误差为2.3 μm,验证了所采用的齿轮视觉测量系统具有较高的稳定性,能够满足齿轮参数在线快速准确测量的要求。 工业齿轮加工现场环境复杂,对加工后的齿轮进行在线测量时不可避免地会受到各种噪声影响。因此,研究如何降低噪声对齿轮在线测量精度的影响,提高图像边缘检测的精度和速度成了齿轮视觉测量技术研究的关键。本文利用搭建好的齿轮视觉测量平台采集齿轮原始图像,在MATLAB R2018a软件环境下采用所提出的方法对齿轮图像进行参数测量,实现了对齿轮各几何参数的准确计算。为了验证本文齿轮参数测量方法的稳定性和精度,最后进行了对比实验来定量分析,实验结果表明所提出的齿轮视觉测量方法能够满足齿轮参数检测的要求,所采用的组合形态学边缘检测算法相比于其他边缘检测算法具有更高的测量精度,和良好的抗噪性。
2.3 齿轮图像边缘检测




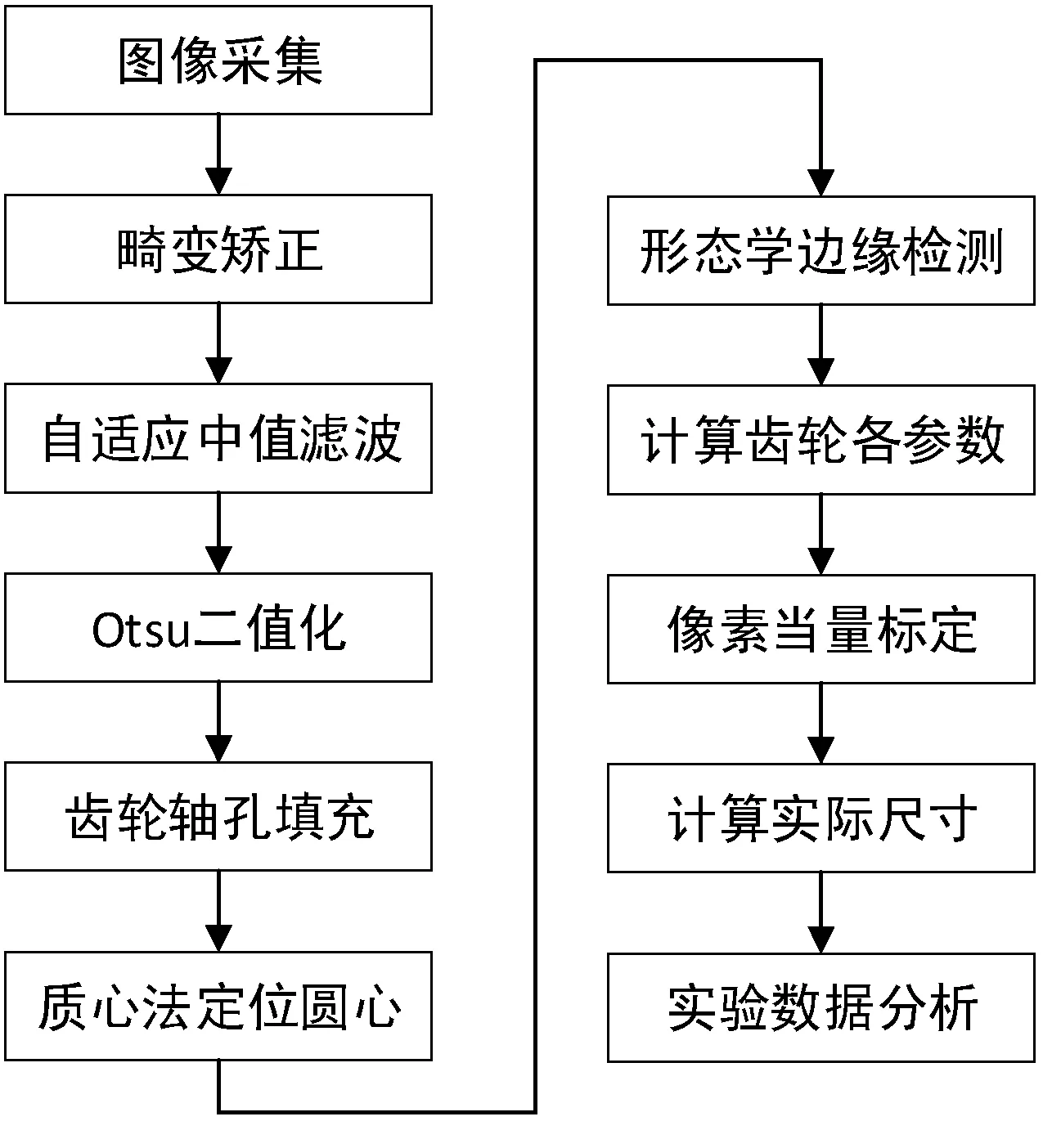
3 齿轮几何参数测量
3.1 齿轮中心点定位

3.2 计算齿顶圆半径和齿根圆半径
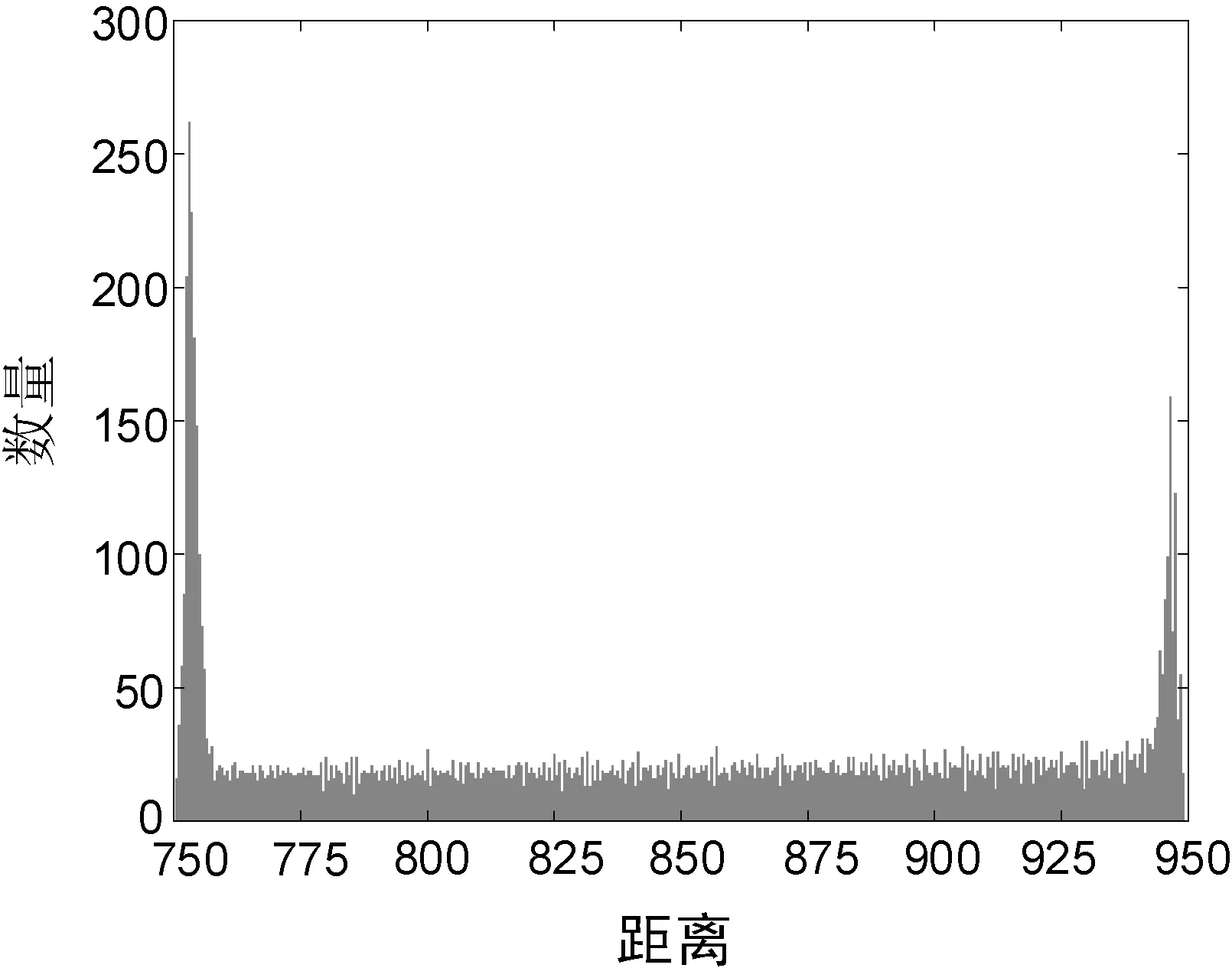
3.3 计算齿数

3.4 计算模数
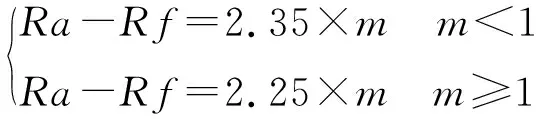
4 实验结果分析

4.1 像素当量标定
4.2 实验数据分析
5 结 语

