异构身份联盟中基于本地差分隐私的信任评估算法

毛一凡 赵 涛 于鹏飞 高先周 杨如侠

1(国家电网有限公司大数据中心 北京 100031) 2(全球能源互联网研究院有限公司 江苏 南京 210003) 3(信息网络安全国网重点实验室 江苏 南京 210003)

0 引 言

随着网络技术的不断发展，网络空间中不同体系结构、不同应用领域的异构网络协同并存，如何统一管理网络实体的多域多形态身份是一个挑战性问题。针对该问题，构建信任联盟实现网络身份管理，已经成为学术界和产业界的共识。微软的Passport[1]、Google基于OpenID协议[2]建立的Google Accounts及CICP服务已形成商用化的身份管理联盟，能够为用户提供联盟内一致的身份和账户管理，将用户身份的有效域从单一机构扩展到联盟范围。然而，在跨域信任联盟中依然存在着一些问题，如身份认证[3]、跨域信任评价等。本文将针对联盟体系中信任评价问题进行深入的研究。

异构身份联盟体系中存在多个身份管理域，在单个评价周期内，每个身份管理域根据域内用户的状态、行为以及历史记录，分析获得用户身份可信程度的评价值，并将该评价值共享给其他身份管理域以形成联盟内对用户的综合可信度评价。该综合可信度评价结果将为各个域对用户访问服务/资源的权限管理提供重要依据。其中,身份管理域内获取的用户可信度评价对该身份域而言可能是敏感信息。每个身份域不想将其产生的对用户的真实评价结果直接暴露给其他身份域。从一方面来说，在身份域共享用户可信度评价结果时，可能被某些用户截获，当用户发现自己评价较低时，或许会采取脱离该身份域等行为，这可能对身份管理域产生一些不好的影响；另一方面，身份域在获知其他域共享来的用户真实评价后，有可能会在用户的评价结果中加入主观因素的考量，从而无法得到身份域对用户客观真实的评价结果。因此，本文将借助本地差分隐私[4-6]设计相应的隐私保护机制，使得身份域在共享用户可信度评价时能够隐藏其隐私信息，同时仍然能够计算出对用户的综合可信度评价结果。

1 基础知识

1.1 本地差分隐私定义

定义1(本地差分隐私ε-LDP[4-6])一个随机化的算A:D→O满足ε-本地差分隐私(LDP)，当且仅当对于任意的输入d,d′∈D，以及任意的输出o∈O，其满足：

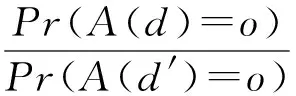
(1)

式中：ε被称为隐私保护预算(ε≥0)。ε在一定程度可以衡量隐私保护程度的大小，由式(1)可知，ε越小(大)，任意两个不同的输入(d,d′)经过算法A之后得到相同输出(o)的概率也就越大(小)，则d与d′的不可区分程度也就越高(低)。

1.2 多元随机响应机制(K-RR)

最初为了保护人们在敏感问题调研中的个人隐私(例如：您曾经是否有过作弊？)，Warner[7]提出了二元随机响应机制。在该机制下，被调研的用户在回答问题之前，先抛掷一枚有偏的硬币(即，正面朝上的概率为p，p>0.5)。如果用户掷到正面，则提供他正确的回答，反之，则给出错误的答案。当调研者(收集者)收集到足够用户的数据之后，则可根据式(2)估算出人群中真实数据为“是”的频率p(′yes′)：

(2)

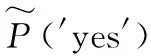
当输入为多元数据，即类别数量为K(K≥2)的类别数据时，其处理与二元随机机制类似，每个用户以p(p>0.5)的概率提供自己真实的类别数据，以1-p的概率从其余K-1个类别中随机抽取一个类别数据进行提交。收集者收到足够数据之后，通过式(3)即可估算出某一类(k,k∈{1,2,…,K})的频率：

(3)

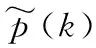
(4)

1.3 Duchi均值机制

当对数值型数据求均值时，通常可以在数据中加入均值为0的拉普拉斯噪声来实现差分隐私的保证(拉普拉斯机制[8-9])。然后，将加过噪声的数据进行相加即可得到无偏的和值以及均值。然而，当ε较小时，须要加入方差较大的噪声来满足其隐私保护程度，这将导致最终得到的估计结果准确度偏低。随后，Duchi等[10-11]提出了一种新的满足本地差分隐私的均值计算方法。在该机制下，假设用户的数据范围为[-1,1]，每个用户通过以下概率对自己的真实数据d(d∈[-1,1])进行变换：

(5)

2 本地差分隐私下的联盟体系内信任评价方案

2.1 问题描述

异构身份联盟体系中包含多个服务提供者，它们形成了多个身份管理域，其中每个域涵盖了一个或多个服务提供者。在一个评价周期内，每个域对其所拥有的用户等实体的可信度进行评价，并将其所得到的用户可信度传递给联盟内的其他用户管理域，最终形成联盟内对用户的综合可信度评价。

假设联盟中共有n个身份管理域，其中，令Cij表示域Ri(i∈{1,2,…,n})对用户uj在某一周期内的可信度评估结果，通常Cij的取值是0到1范围上的实数，即Cij∈[0,1]。通过表1可将实数表示的Cij对应转换成离散的可信度级别Tij,Tij∈{1,2,…,5}。

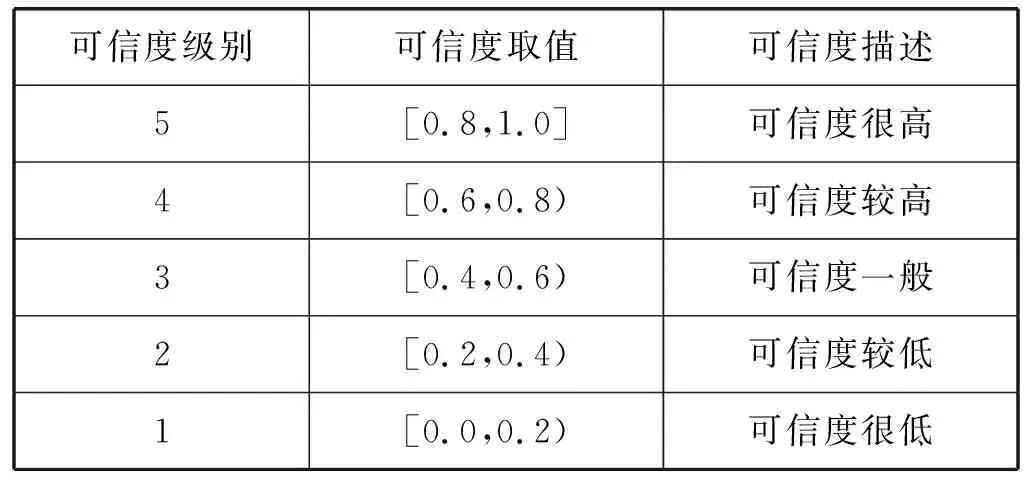
表1 用户可信度相对关系

然后每个域Ri将转为离散数据的可信度评价结果Tij共享给其余n-1个域。接收到其余域对用户uj的评价之后，Ri通过均值计算则可获得该周期内联盟中对用户uj的总和评价结果Zj，即Zj=mean(T1j,T2j,…,Tnj)。

然而，每个域对用户的评价结果都是敏感的，它们不愿将自己对用户的真实评价公布给其他的身份域。因此，本文将借助本地差分隐私技术设计具有隐私保护效果的信任评价方案，实现对身份域评价结果的隐私保护，同时也能够使每个身份域获得联盟中对用户的综合评价。

2.2 基于Duchi机制的信任评价方案(DTM)

本文采取Duchi求均值的机制实现对每个身份域敏感信息(用户信任评价结果)的隐私保护，并获取多个身份域评价结果的均值信息。由于Duchi机制中的数据范围为[-1,1],因此，每个身份域Ri首先须要对所得的用户可信度级别(Tij)做一个幅度缩放，将其映射到[-1,1]的范围上：

(6)

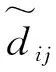
算法1DTM

输入：身份域Ri对用户uj的可信度级别Tij，隐私预算ε。

1) 根据式(6)对真实的可信度级别Tij进行幅度缩放，并将缩放后的数值标记为dij。

2) 将dij按照以下概率进行变换：

(7)

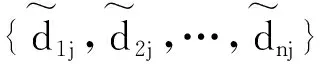
定理1方案DTM满足ε-本地差分隐私。

证明在该证明中，令A代表方案DTM。根据本地差分隐私的定义，可以写出：

(8)

或者:

(9)

式中：Tij、dij、Ti′j、di′j是任意两个身份域Ri、Ri′对用户uj的可信度评价以及其缩放后的数值。当dij=1、di′j=-1时，式(8)取得最大值，即为eε；当dij=-1、di′j=1时，式(9)取得最大值，即为eε；综上可得：

因此，该方案DTM满足满足ε-本地差分隐私。

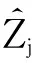
(10)

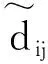
所以：

(11)

其中：

(12)

由式(12)可知，当dij=0时，其方差取到最大值，因此:

(13)

由式(11)与式(13)可得：

2.3 基于多元随机响应机制的信任评价方案(RTM)

2.1节介绍了表1可将每个身份域Ri对用户uj的可信度评估值Cij转换成离散数据型的可信度级别Tij。在计算Zj时，除了把{T1j,T2j,…,Tnj}按照数值相加求平均来做之外，还可将其转化为加权平均值的问题来进行处理，正如式(14)所示。

(14)

式中：t∈T,T={1,2，…,5},表示五个不同可信度级别取值的集合；f(t)代表t在{T1j,T2j,…,Tnj}中出现的频率。此时，求解平均值的问题就转变成求解每个可信度级别频率f(t)的问题。考虑到每个身份域敏感信息的隐私保护问题，本文将借助多元随机响应机制实现差分隐私下的可信度级别的频率估算。

算法2RTM-1

输入：身份域Ri对用户uj的可信度级别Tij，隐私预算ε。

1) 将Tij按照以下概率进行扰乱：

(15)

当身份域Ri接收到全部身份域发送来的可信度级别之后，便可以按照如下公式可以对所有的可信度级别进行频率估计：

(16)

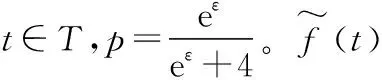
算法3RTM-2

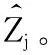
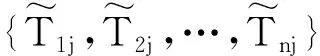
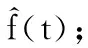
定理3方案RTM-1满足ε-本地差分隐私。

证明在该证明中，令A代表方案RTM-1。根据本地差分隐私的定义，可以写出：

(17)

式中：Tij、Ti′j是任意两个身份域Ri、Ri′对用户uj的可信度评价。根据式(15)可知，当Tij=T*且Ti′j≠T*时，式(17)取得最大值，即eε，所以：

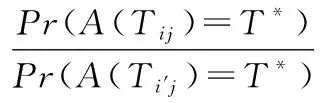
(18)

方案RTM-1满足ε-本地差分隐私。

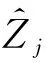
(19)

证明根据式(14)和式(16)，可得：

(20)

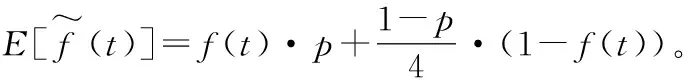
(21)

根据文献[12]中的式(4)，可计算出：

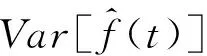
2.4 方案对比

本节将对2.2节和2.3节中的方案进行理论上的对比，分析差分隐私预算的大小对两种方案误差的影响。

定理5当隐私预算ε约大于2.6时，RTM方案下关于综合评价结果估算的方差可小于DTM方案下的方差。

证明由式(10)和式(19)写出：

化简可得：

55·(eε+3)≤4(eε+1)2

165≤4(eε+1)2-55eε

ε≥2.6

3 实验结果与分析

实验部分主要针对本文方案的估算精度进行了深入的分析。具体地，本文想要从隐私保护预算以及参与对某一用户信任度评价的身份域数目两方面，来分析其对综合信任度估算的准确度影响。为了到达上述目的，本文随机生成四个分别包含30条、50条、80条和100条数据的均匀分布数据集，用以模拟30个、50个、80个和100个身份域对某一用户做出的信任度评价。四个数据集中每条数据取值范围均为[0,1]。数据在进行隐私保护之前，需将其根据表1进行离散化，然后再利用本文提出方案中的数据处理算法(DTM-1，RTM-1)对其进行随机扰乱来达到隐私保护目的。实验中用相对误差(RE)来衡量估算出的综合信任度评价与真实值之间的差异：

(22)

实验环境为Intel Core i5 CPU 3.1 GHz，8 GB内存。本文算法均在MATLAB中进行实现，并做出实验图表，实验结果取10次实验的平均值。

为了有效地说明本文算法的可用性，本节将设计的两种算法(DTM，RTM)在不同的隐私预算下进行了对比，并将其趋势呈现在图1中。实验中，差分隐私预算的取值大小分别为{0.5,1,2,4,6,8}。从图1可以看出，在所有数据集上，随着隐私预算ε的增大，两种算法估计结果的误差呈现出下降的趋势，即估算精度逐步提高。此外，在所有数据集上，当隐私预算ε大于2时，RTM算法的估计结果的准确度总是比DTM算法的更加精确，这与2.4节中的理论分析结果相一致。图2中对比了两种算法在相同隐私预算下不同数据集上的表现，即参与评价的身份域数目对估算结果的影响。可以观察到，这与第2节中的误差理论分析相吻合。

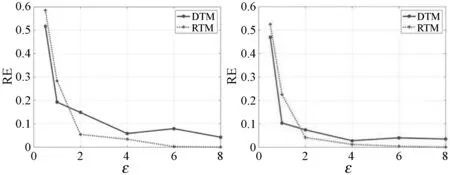
(a) n=30 (b) n=50

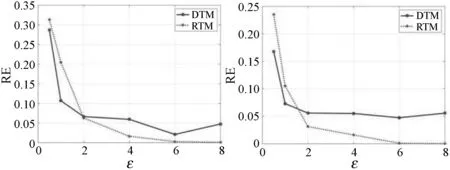
(c) n=80 (d) n=100图1 不同ε取值下DTM与RTM算法的误差对比

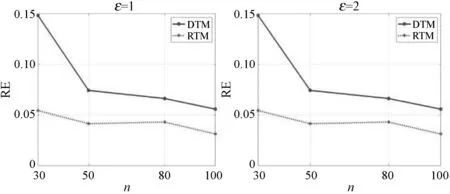
(a) (b)图2 不同数据集下DTM与RTM算法的误差对比

总的来说，当隐私预算ε较小时，DTM方案呈现出较好的优势；当ε逐渐变大后，RTM方案将得到精度更高的估算结果。整体来看，当隐私预算ε取到4时，本文两种方案的估计误差基本不会超过0.05。另外，参与计算的身份域个数也对计算结果的精度有所影响，身份域个数越多，估算出结果更加准确。通过本节的实验，可以证明本文提出的两种算法能够有效达到隐私保护的效果，同时也能估算出较为精确的综合信任度评价。

在目前已有的异构环境下的信任评估工作[13-14]中，多是考虑用户在跨域访问中由于不同系统信任度评价机制不统一造成的对数据访问的安全威胁，还未出现与本文类似的针对用户可信度评价数据的隐私保护工作。此外，与本文均值计算相关的隐私保护方案，除了基于本地差分隐私的均值机制，还存在一些利用安全多方计算技术进行设计的均值计算算法。然而，安全多方计算中多用到密码学工具，虽然可以获得准确的计算结果，但其通信和计算开销往往较大，难以有效地在异构身份联盟环境下应用。

4 结 语

本文主要研究了联盟体系内关于用户综合信任度评估计算中存在的隐私泄漏问题，并基于已有的差分隐私保护机制，设计了两种满足ε-本地差分隐私的综合可信度计算算法。在该算法下，每个身份域在共享对用户的真实评价结果时可以有效地隐藏其真实信息，同时，仍然能够从所有身份域扰乱的评价结果中恢复出对用户的综合可信度评价结果。通过理论分析和实验验证，该算法能够达到相应的隐私保护效果，并能获得高准确率的计算结果。