基于CNN的安防数据相似重复记录检测模型

王 巍 刘 阳 洪惠君 梁雅静

1(河北工程大学信息与电气工程学院 河北 邯郸 056038) 2(河北省安防信息感知与处理重点实验室 河北 邯郸 056038) 3(江南大学物联网工程学院 江苏 无锡 214122)

0 引 言

随着信息化时代的飞速发展，每个行业每天都会产生大量的数据，安防行业也不例外。在安防行业中，部分结构化的信息还需要以手工录入、人为修改的方式进行[1]。这种方式不但效率低，而且会产生许多的脏数据，会直接影响到各类事件的后续处理效率。这些脏数据的表现形式主要有相似重复记录、缺失数据、冲突数据和错误数据等几种类型[2]。其中数据源中存在相似重复记录是最严重的问题之一，严重时可能会导致数据失效。因此相似重复记录的检测及清除一直都是研究的热点。

当前常见的相似重复记录检测算法主要有编辑距离算法(Levenshtein Distance)、Smith-Waterman算法、N-gram算法和机器学习算法等。陈俊月等[3]提出了基于词向量的编辑距离算法，改进了传统的编辑距离算法和Jaccard系数，将编辑距离的删除和插入两种编辑操作修改为空字符与目标字符的替换操作，通过词向量计算每种编辑操作的相似度并累加，得出改进的编辑距离相似度。文献[4]改进了编辑距离算法，使用同义词词典替换了传统的语法变异的方法，对于存在大量语法错误和拼写错误的问题的数据集，可有效提高算法的精度。文献[5]利用依赖图的传递闭包和循环倾斜提出了一种Smith-Waterman算法并行化的方法，将精确传递闭包的方法替代为近似传递闭包，在现代多核计算机中加速效果显著。文献[6]对比了三种基于统一计算设备架构(Compute Unified Device Architecture,CUDA)的Smith-Waterman算法的并行计算方法，分别是粗粒度加速方法、细粒度加速方法和重新定义递归公式的方法。其中：粗粒度加速方法可利用GPU同时处理多个对齐，但是不同线程处理长度不同的序列的时间不同，导致处理短序列的线程等待时间较长；细粒度加速方法可以利用多线程计算DP矩阵，减少了中间计算的时间，但是在计算开始和结束的阶段都需要花费大量的时间；重新定义递归公式的方法重新定义了Smith-Waterman算法的递归公式，将算法时间复杂度从O(mn)降低到了O(mlog2n)，其中m和n表示任意两条记录的长度，提高了算法的效率，但不能对差距的扩大给出不同的罚分。王常武等[7]提出了一种加权的N-Gram相似重复元数据记录检测算法，对于不同的标签在相似重复记录检测的过程中的重要程度赋予不同的权重，依据权重使用加权的N-gram算法进行相似度计算，实验表明，加权后的N-gram算法优于普通的N-gram算法。陈亮等[8]使用分块技术根据字段对数据排序并分块，使用滑动窗口的思想提升检测效率，然后将各字段得出的分块一起聚类，对重复率较大的分块对首先比对，并放弃聚类效果较差的分块，最终通过降低聚类次数和放弃聚类效果较差的分块的方式提升了效率和准确率。

近年来机器学习成了研究的热点，几乎在各行业都有应用案例，也有研究人员运用机器学习算法来检测相似重复记录。相似重复记录的检测在机器学习中可以看作分类问题中的二分类问题。吕国俊等[9]提出了一种基于多目标蚁群优化的支持向量机的相似重复记录检测方法，该方法将相似重复记录描述为一个二分类问题，同时考虑到相似重复记录中重复样本很少的问题，只用不相似重复记录样本进行训练。文中的实验结果验证单类支持向量机算法的有效性。张攀[10]将BP神经网络运用到相似重复记录的检测当中，用两条记录相同字段间的编辑距离组成的向量作为BP网络的输入数据，并为其添加上标签训练出BP网络，然后使用训练出的BP神经网络检测两条记录是否为相似重复记录，实验结果表明，在数据生成器“febrl”生成的数据中，基于BP神经网络的相似重复记录检测方法的准确率可达97%以上。孟祥逢等[11]首先融合Jaro算法与TF-IDF算法计算字段相似度，然后使用经过遗传算法优化的神经网络计算两条记录的相似度，可以有效提高检测的准确率和精度，但在中文数据中的效果还有待商榷。

尽管上述相似重复记录检测算法的精确率(Precision)和召回率(Recall)等指标都已经达到了较高的水平，但是上述数据大部分是开源的数据集，实际应用中的数据集存在更复杂的情况。在安防数据库中，由于不同信息录入员的不同习惯，存在大量空值、错误值、串字段错误和各种符号等干扰信息，对相似重复记录的检测产生了一定的影响，同时安防数据中部分相似重复记录肉眼辨别都需要较长时间。例如表1中前两条记录表述不同，但实际含义相同，是相似重复记录，而后两条记录虽然仅存在个别字不同，但其是两个不同的加油站，不是相似重复记录。因此，安防数据相似重复记录的检测难度比网络上开源的数据集要高，需要开发一种适用于安防数据的相似重复记录检测模型，检测出尽可能多的相似重复记录对，同时还需要较强的泛化能力。卷积神经网络(Convolutional Neural Networks,CNN)是深度学习的代表算法之一，在深度学习中的研究最为广泛[12]。近年来，CNN开始应用于文本分类等自然语言处理领域，并且取得了一定的成果。例如，文献[13-14]将CNN应用于文本情感分类；宋岩等[15]使用CNN对文本进行分类；肖琳等[16]使用CNN对文本进行多标签分类；张璞等[17]结合CNN与微博文本特征对用户性别进行分类等。

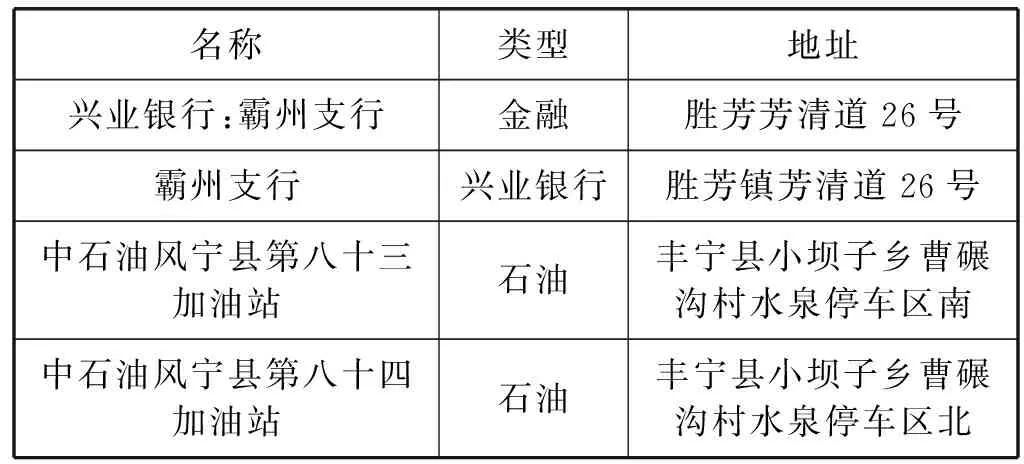
表1 安防数据相似重复记录示例

因此，本文设计一种基于CNN的安防数据相似重复记录检测模型。通过对在手写数字识别上拥有不错效果的LeNet- 5进行改进，得出了两种适用于安防数据的相似重复记录模型，一种是以词向量矩阵为输入的CNN模型(Word Embedding Matrix CNN,WE-CNN)，另一种是以相似度矩阵为输入的CNN模型(Similarity Matrix CNN,SIM-CNN)。然后分别对这两种模型进行了介绍，并通过了K折验证，使用精确率、召回率和F1值(F1 Score)等评价指标对模型进行了评价。

1 数据预处理

为了提高模型的效率和可靠性，在训练模型之前，需要对数据进行预处理，并且需要将每条记录中的每个词都转换为模型可以识别的词向量(Word Embedding)。根据安防数据存在的问题以及安防数据的特点，本文将数据预处理主要步骤分为分词和词向量生成两部分，具体流程如下：

(1) 字段选择。手动选择数据库中对于任意两条记录是否为相似重复记录影响较大的字段，并且删除数据库中的空记录等无效的记录。

(2) 分词。对记录中的每一个字段进行中文分词，并删除停用词、标点、特殊字符等内容。本文采用“jieba”分词工具进行分词。将每条记录分词后的内容按照字段顺序组成一个列表，也就是一个列表对应一条记录，则第i个列表的长度L(i)表示为：

(1)

式中：n为字段数；lif为第i个列表的第f个字段分词后的词语的个数。

(3) 训练词向量。对分词后的所有列表进行词向量的训练，得出每一个词的词向量c。本文采用Google的“Word2vec”工具训练词向量，主要参数如表2所示。其语料库为本文的实验数据某安防报警网络公司用户数据。

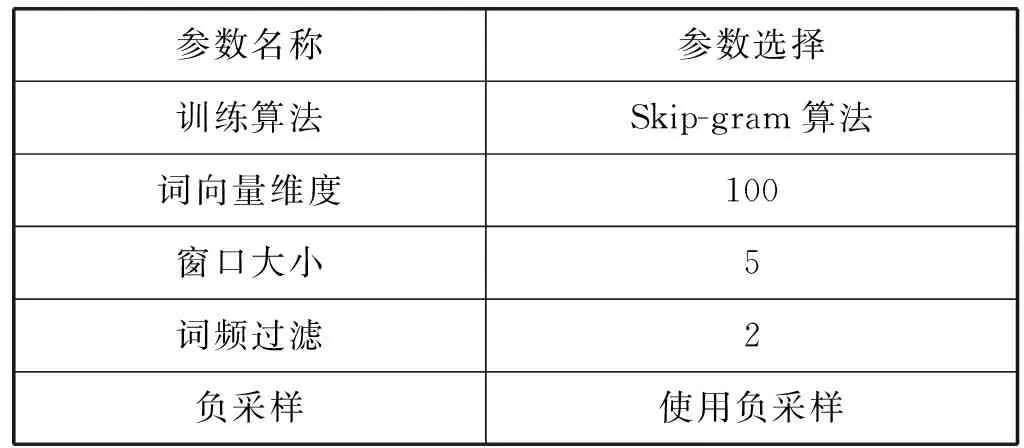
表2 “Word2vec”词向量训练工具主要参数

表2中的Skip-gram算法使用中心词预测周围词语，根据预测结果修正中心词词向量。通过对安防领域数据的验证，大部分字段为中文短句或者长词组，每个词与前后词的关联较大，并且这些短句或者长词组对两条记录是否为相似重复记录影响较大，因此对于安防领域数据，可使用“Word2vec”的Skip-gram算法训练词向量。

(4) 合成矩阵。将每一个记录中的所有词语对应的词向量组成一个向量组，该向量组就是词向量矩阵。假设第i条记录的词向量矩阵是Vi，则该矩阵表示为：

Vi=[c1,c2,…,cL(i)]

(2)

使用Word2vec中的相似度计算算法，计算出两条记录m和n中所有词之间的相似度，组成相似度矩阵S，表示为：

(3)

(5) 统一矩阵大小。统一各词向量矩阵的矩阵大小和各相似度矩阵的矩阵大小，根据分词后的每一个列表的长度L(i)(i∈N且i∈[0,n)，n是数据库中删除无效记录后的记录数)，选择合适的矩阵大小，不足的部分补充0，超出的部分删除。如果选择的矩阵大小太小，无法包含记录的有效信息，相反，过大会降低计算的效率。图1为本文选用的安防数据记录对应的记录长度比例分布图，横坐标表示记录长度，纵坐标表示小于等于某长度的记录与全部记录的数量比。可以看出95%左右的记录长度都在60以下，因此本文的词向量矩阵大小为60×100，相似度矩阵大小为60×60。

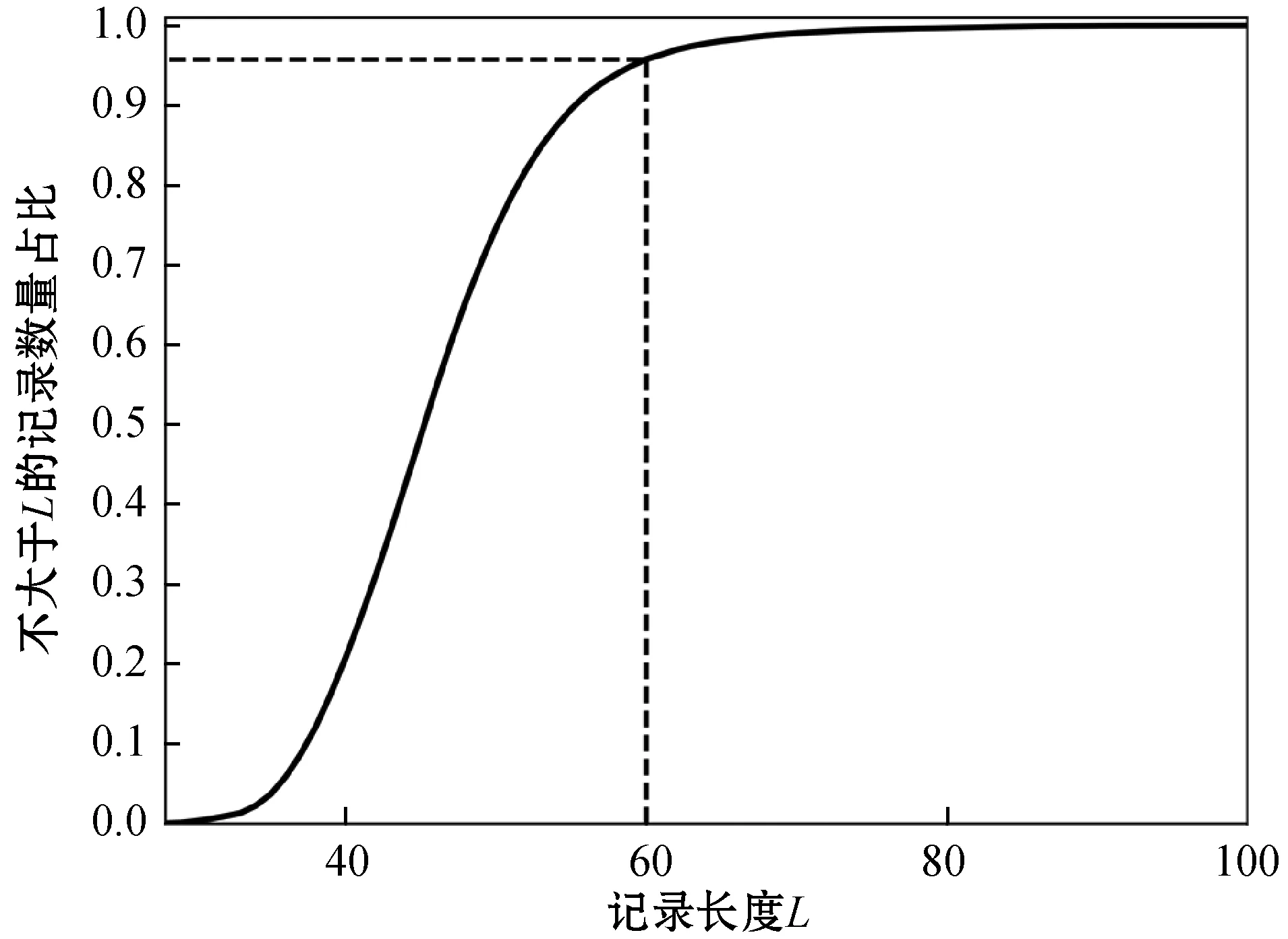
图1 安防数据记录长度比例分布

(6) 标记数据。标记两条记录m和n是否为相似重复记录，并将m和n词向量矩阵与标签组成带标签的词向量矩阵数据。将两条记录m和n组成的相似度矩阵与标签组成带标签的相似度矩阵数据。

上述流程如图2所示。

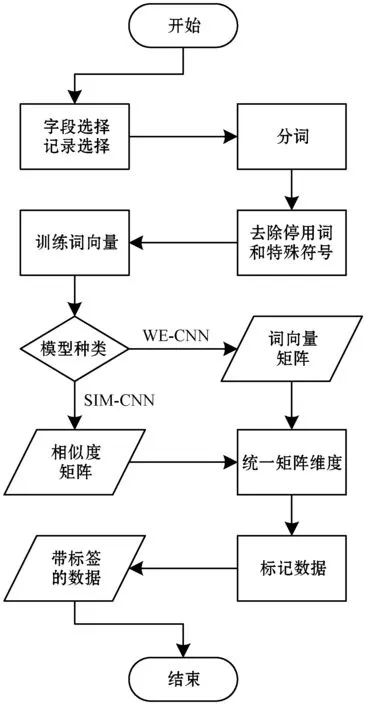
图2 数据预处理流程

2 模型设计

2.1 LeNet- 5模型

Fukushima[18]最早提出了卷积神经网络，除去输入层和输出层，卷积神经网络通常还包含若干个卷积层、池化层和全连接层。LeNet- 5[19]是出现时间最早的卷积神经网络之一，由Yann LeCun提出，最早应用于手写体识别。LeNet- 5的结构如图3所示。

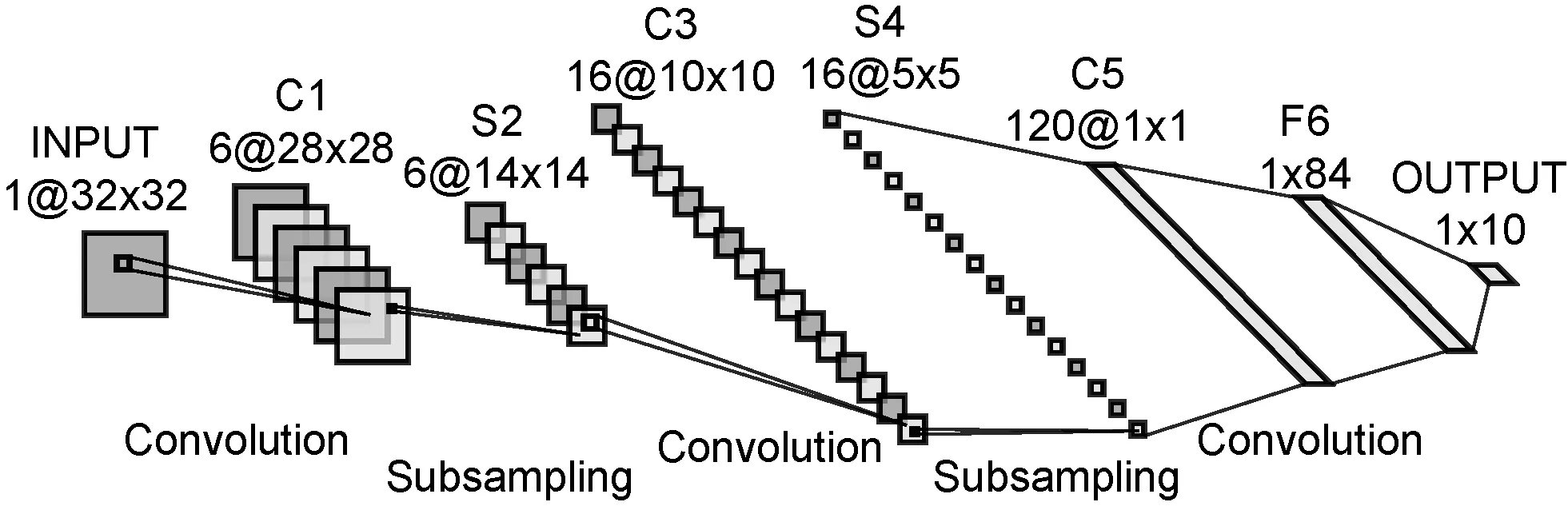
图3 LeNet- 5结构

LeNet- 5一共有8层，包括：3个卷积层C1、C3和C5；两个池化层S2和S4；一个全连接层F6；一个输入层INPUT和一个输出层OUTPUT。其中INPUT层的输入是1幅维度为32的图片；C1层通过6个5×5大小的卷积核得出6幅维度为28的特征图；S2层将上一层特征图中2×2范围内的数值相加并乘一个系数加一个偏置，得出6幅维度为14的特征图，这个过程称为二次采样(Subsampling)，其中的系数和偏置可训练；C3层采用部分映射的方式将S2层的6幅特征图通过5×5大小的卷积核转换为16幅10×10的特征图，表3展示了具体对应的方案，其中的数字为特征图(通道)号；S4层通过二次采样，得出16幅5×5的特征图；C5层用5×5的卷积核对5×5的特征图进行卷积操作，将S4层的16幅特征图转换为120幅1×1的特征图；F6层包括84个单元，并且完全连接到C5层。OUTPUT层有10个欧氏径向基函数单元，表示十个手写数字，可得到图片是哪个手写数字。

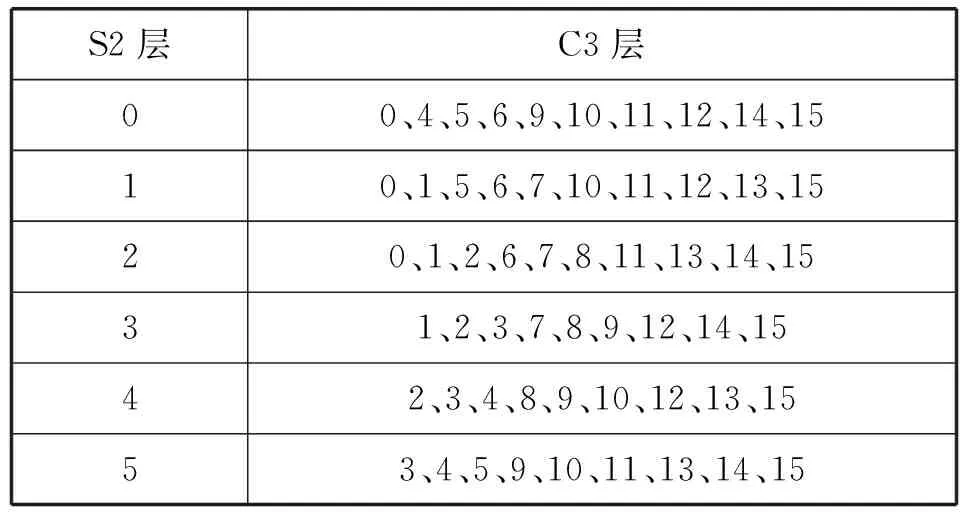
表3 S2与C3的连接方案

2.2 改进的LeNet- 5模型

(1) WE-CNN模型。与复杂的图像识别相比，文本识别的复杂度要低一些。而LeNet- 5可以识别较为简单的手写体图片，所以将LeNet- 5应用于相似重复记录的识别具有一定的可行性。为了让LeNet- 5模型适用于文本识别，并且可以有效解决安防数据相似重复记录检测存在的无法填补的空值、串字段等难点，本文设计以记录的词向量矩阵为输入的CNN模型WE-CNN，模型在LeNet- 5的基础上进行改进，改进后的模型如图4所示，具体做了以下几个部分的改进。

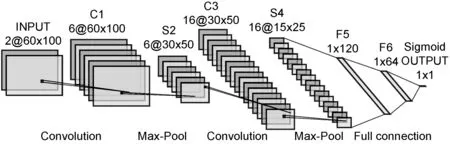
图4 WE-CNN模型结构

在LeNet- 5中，输入维度为32×32，为了保证得到更全的细节特征，提高模型的识别率，将输入的维度修改为与数据预处理中描述的60×100，同时因为要判断两条记录的相似度，所以输入的通道数为2。

为了简化算法，将S2层与C3层之间的连接方案改为全映射；把C5层改为全连接层并改名为F5，这样可以更好地将特征矩阵中的信息传递下去，这里涉及的特征矩阵对应LeNet- 5中的特征图；C1层和C3层均采用3×3的卷积核，并且将卷积操作的填补(padding)设置为1，在进行卷积操作时可以不改变特征矩阵的维度，在简化各层之间的维度计算的同时可以保留更全的信息；将S2层和S4层中的二次采样修改为最大池化(Max-Pool)，可以保留记录中更多的边缘特征。

由于相似重复记录检测问题属于二分类问题，故将模型的输出从十个改为一个，并使用Sigmoid函数，将输出值转化为一个介于0到1之间的概率值，概率值越接近1，表示输入的两条记录为相似重复记录的可能性越大，反之不是相似重复记录的可能性越大，区分是否是相似重复记录的阈值通常取0.5。

为了防止出现过拟合的现象，在S2层与C3层之间、S4层和F5层之间、F5层和F6层之间、F6层和OUTPUT层之间均加入Dropout方法。Dropout方法可以随机丢弃p%的神经元，使用剩下的神经元进行训练，可以防止过拟合和增强模型的泛化能力。为了减轻梯度消失问题对模型的影响，在S2层、S4层、F5层、F6层和F7层均设置一个tanh函数。

使用Adam算法作为模型的优化算法。Adam算法结合了Momentum算法和RMSprop算法中的更新方向方法和计算衰减系数方法，式(4)为Adam算法的算法策略。

(4)

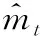
在二分类问题中，可以采用适用于二分类问题的交叉熵损失函数函数(Cross Entropy Error Function)作为模型的损失函数，式(5)为该函数的表达式。

(5)

式中：n是批量大小(batch size)；x是模型实际输出的值；y是标签上的值，也就是目标值。

(2) SIM-CNN模型。在安防行业中，某些数据会有极高的质量要求，为了进一步提高数据的质量，在WE-CNN模型的基础上，提出以相似度矩阵为输入的CNN模型SIM-CNN。从理论上来说，与WE-CNN模型相比，在同样的数据源下，SIM-CNN模型应该具有更高的识别率，但是SIM-CNN模型所需的相似度矩阵生成的时间较长。

除了输入层，SIM-CNN与WE-CNN模型的其余部分完全相同。SIM-CNN的输入为通道数为1的相似度矩阵，根据数据预处理中的描述，将输入的相似度矩阵维度设置为60，模型的结构如图5所示。

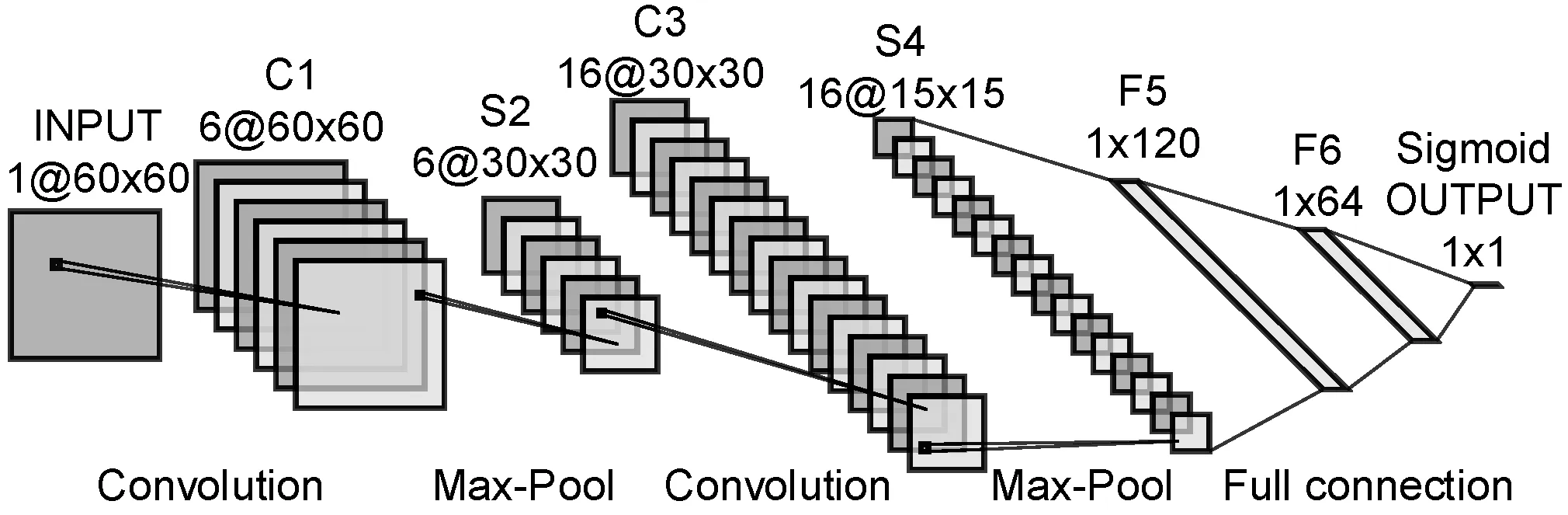
图5 SIM-CNN模型结构

3 实验验证

本次实验首先对实验数据、实验环境和实验中用到的一些评价方法进行了介绍；然后对模型中的部分参数进行了选择分析，并对模型的效果、泛化能力进行了验证；最后与BP神经网络进行了对比。

3.1 实验数据说明

实验采用某安防网络报警公司的用户数据作为实验数据，一共有32 480条记录，120个字段。经过筛选，得到了30 513条有意义的记录，26个对相似重复记录的识别影响较大的字段。经过初步判断，实验数据中有6 100对左右的相似重复记录。

本次实验选取了11 000对记录作为训练数据和测试数据，其中相似重复记录和不是相似重复记录的数据各5 500对。

3.2 实验环境

实验的硬件环境配置如表4所示。

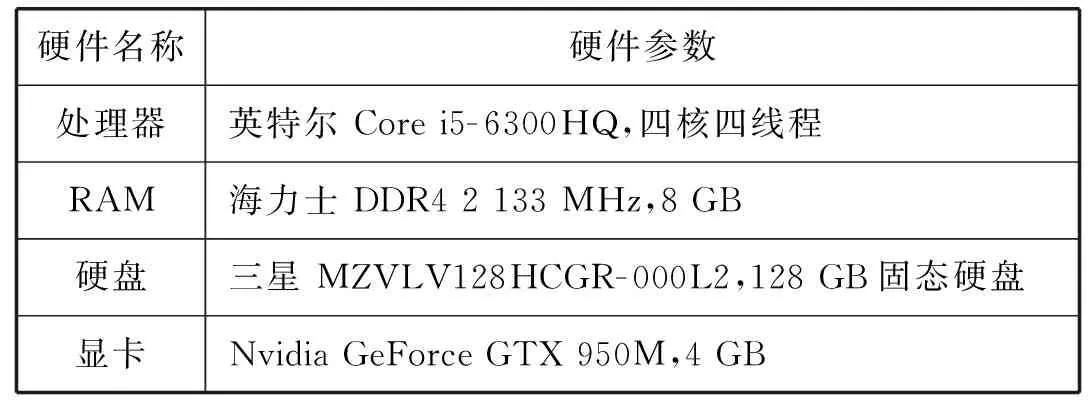
表4 实验硬件环境

本实验采用了CUDA并行计算架构，实验的软件环境如表5所示。

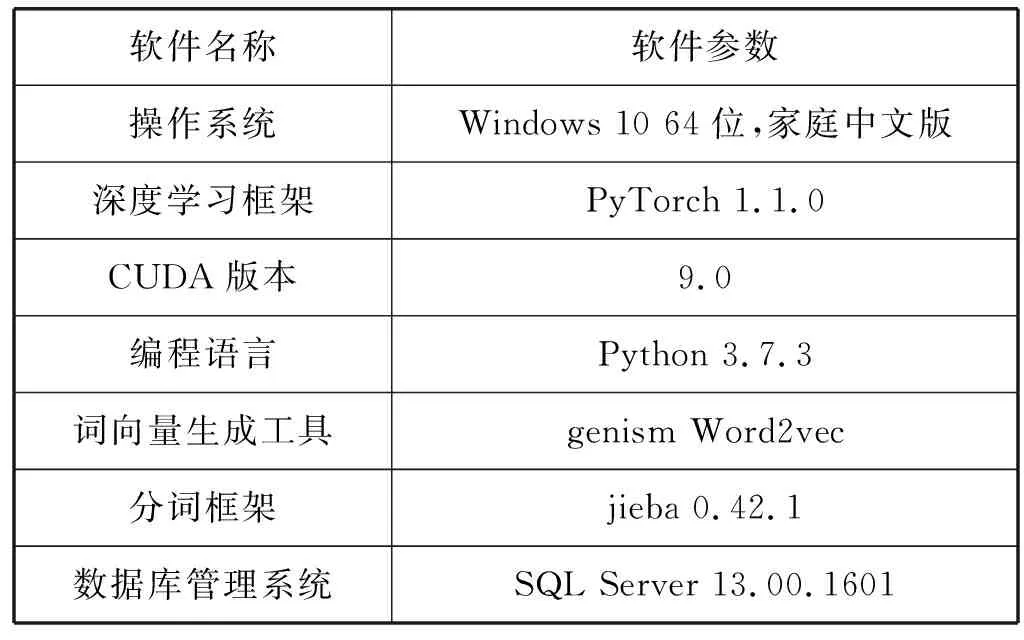
表5 实验软件环境

3.3 实验评价方式

为了评价模型的优劣，引入了精确率、召回率和F1值等评价指标。精确率、召回率和F1值分别可以用式(6)-式(8)表示。

(6)

(7)

(8)

假设将不是相似重复记录记为正类，是相似重复记录记为负类，则式(6)-式(8)中：TP表示实际上和预测的都不是相似重复记录的数据对的个数，记为真正类；FN表示实际上不是相似重复记录，预测是相似重复记录的数据对的个数，记为假负类；FP表示实际上是相似重复记录，预测不是相似重复记录的数据对的个数，记为假正类；TN表示实际上和预测的都是相似重复记录的数据对的个数，记为真负类。

为了验证模型的可靠性，引入K折交叉验证的方法对模型进行分析。K折交叉验证是将数据分成K组，使用任意一组作为测试集，剩余的K-1组作为训练集，迭代K次，让每一组数据都做过一次测试集，每次迭代的测试集中的数据不会出现在当次迭代的训练数据中。

3.4 实验结果和分析

(1) 学习速率选择实验。在批量大小batch-size都为64，迭代次数epoch都为60，以及其他参数都相同的情况下，从0.01、0.005、0.001、0.000 5和0.000 1五个学习速率当中确定合适的学习速率。从理论上来说，在各参数都相同的条件下，如果学习速率较大，可能会出现发散的情况，如果学习速率越小，收敛速度越慢。本实验中，在学习速率在0.01时，两个模型出现了损失发散的情况，在学习速率为0.005时，WE-CNN模型存在低概率的发散，故舍弃这些导致损失发散的学习速率。两个模型在不同学习速率下的各项指标如图6和图7所示。

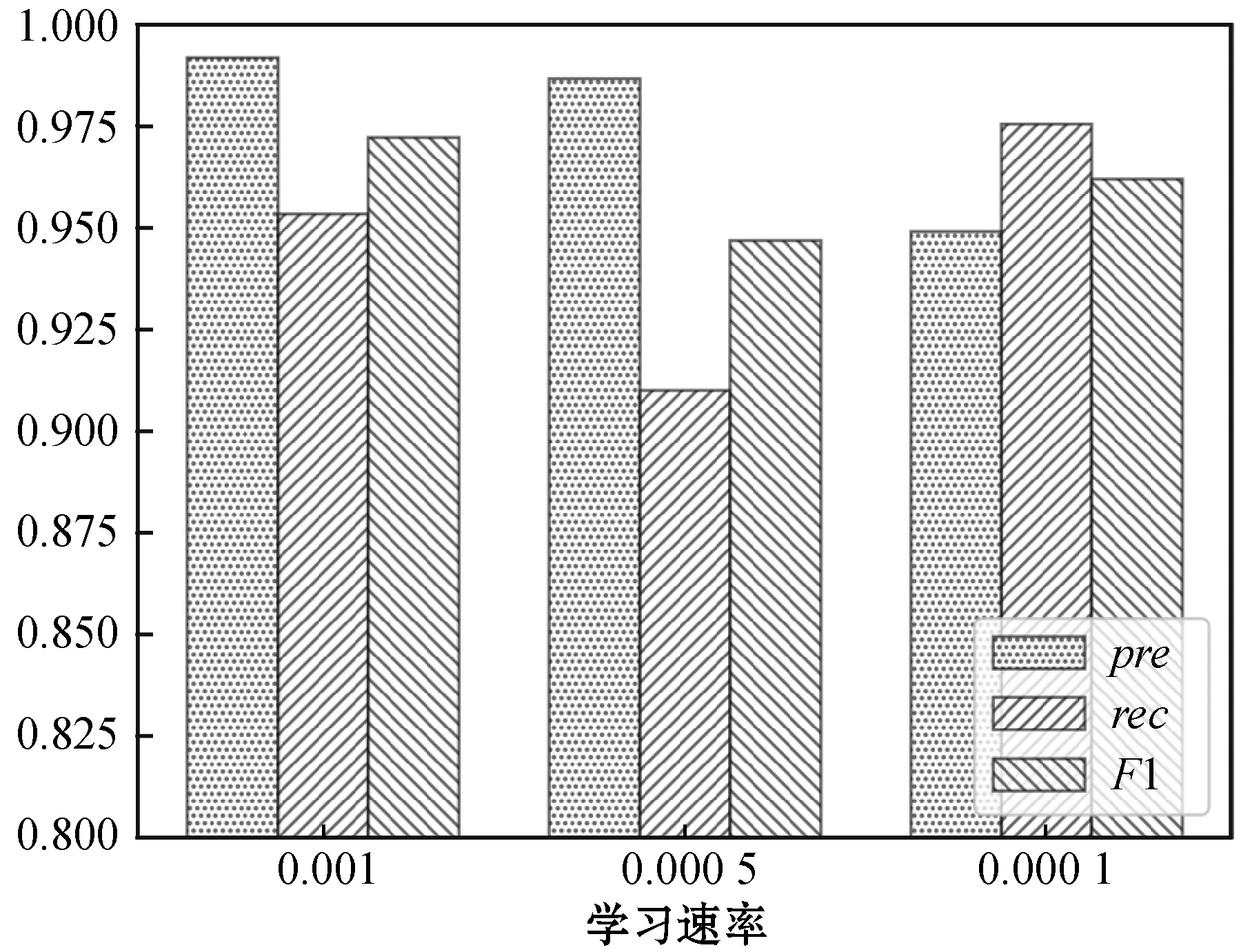
图6 WE-CNN模型不同学习速率下的表现

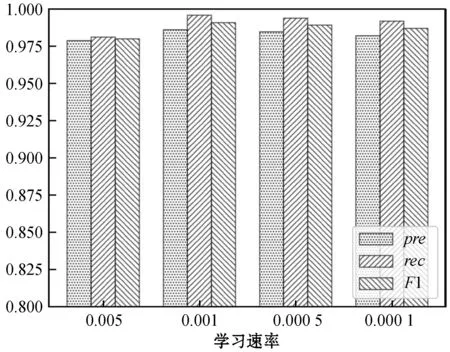
图7 SIM-CNN模型不同学习速率下的表现

从图6中可以看出，WE-CNN模型的学习速率为0.001时的整体效果最好，其F1值最大，但是召回率较低；从图7中可以看出，当SIM-CNN模型在学习速率为0.001、0.000 5和0.000 1时，精确率、召回率和F1值都很接近，并且都在0.975以上，不过学习速率等于0.001时的SIM-CNN模型略优于其他学习速率的模型。这是因为随着迭代次数的增加，学习速率为0.001的模型可以最先达到最优结果。所以在本实验的测试数据集中，WE-CNN模型和SIM-CNN模型的学习速率在0.001时模型的表现最优。

(2) Dropout对模型的影响。表6介绍了是否使用Dropout优化方法对模型的影响。可以得出WE-CNN模型在不使用Dropout优化方法时会对模型的识别能力产生较大的影响，因为每次训练都是使用相同的模型，所以出现了过拟合现象。而使用Dropout可以使神经元随机失活，每次训练的模型都不同，因此不容易出现过拟合现象，识别率相对更高。SIM-CNN模型在不使用Dropout优化方法时同样会对模型的识别能力产生影响，所以使用Dropout优化方法可以有效防止过拟合，增强模型的识别能力。

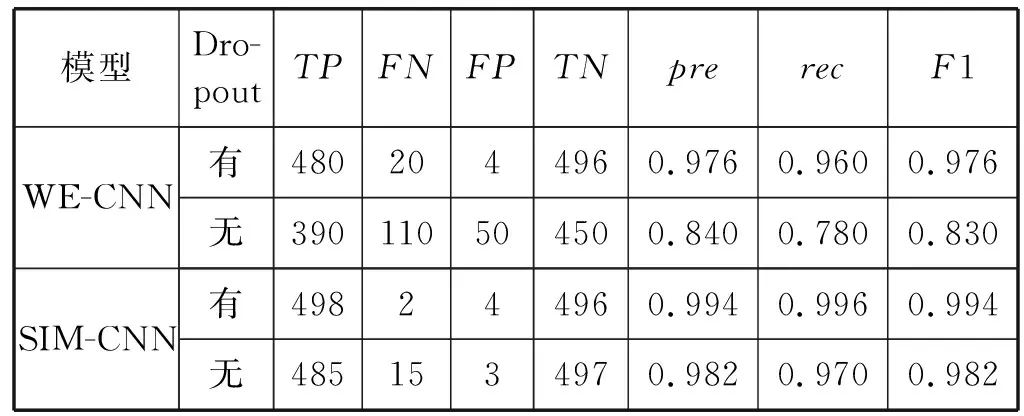
表6 Dropout优化方法对模型的影响

(3) K折交叉验证。根据K折交叉验证的规则，将本次实验的11 000个样本，分成了11组数据，每组数据中都有500个正类样本和500个负类样本。从第1组样本开始，依次将该组数据作为测试集，并将剩余的数据作为第1组的训练集。将学习速率设置为0.001，批量值batch-size=64，迭代次数epoch设置为60，阈值设置为0.5，通过WE-CNN模型在所有的训练集进行训练，并使用每个训练集对应的测试集对模型进行测试，使用式(5)所示的交叉熵损失函数计算损失，得出K折验证中每个测试集的精确率、召回率和F1值。WE-CNN模型的K折交叉验证的各项指标如表7所示。

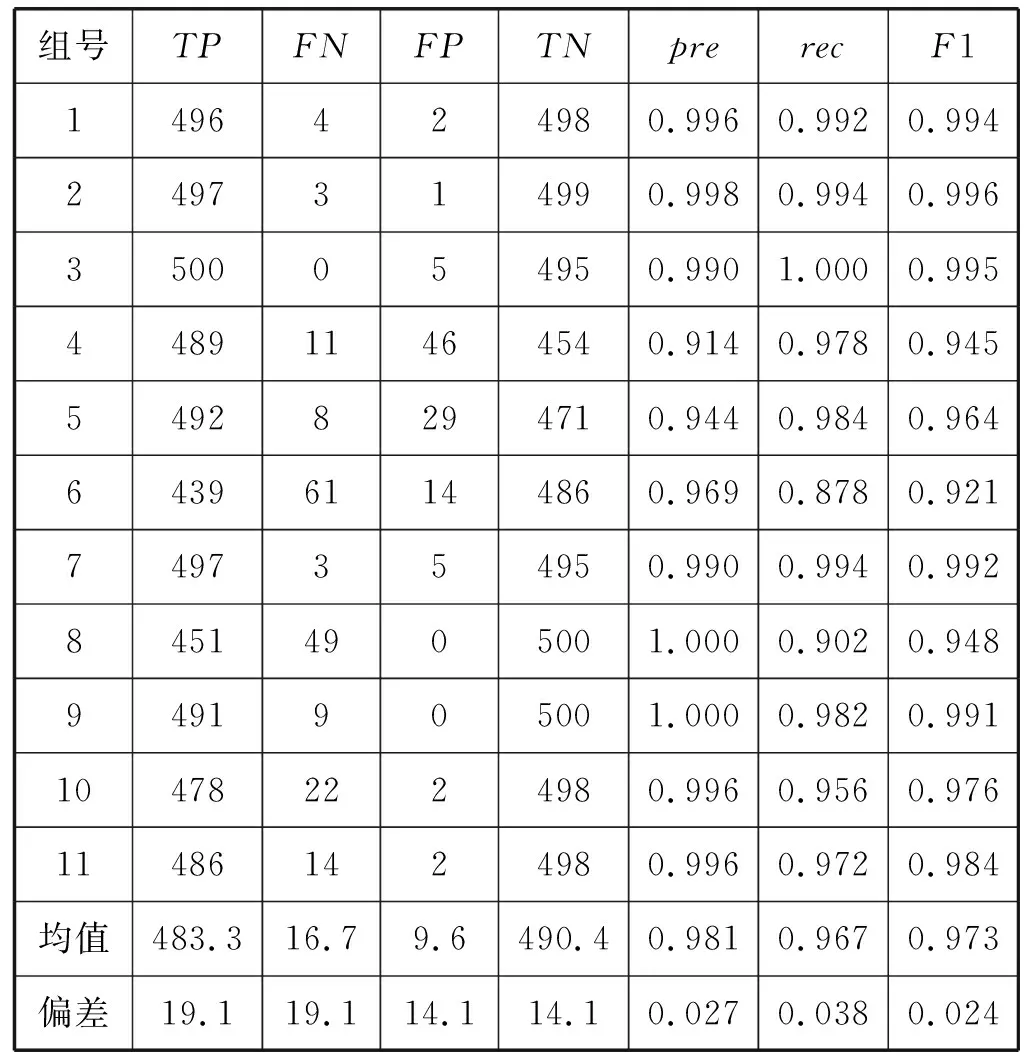
表7 WE-CNN模型K折交叉验证各项指标

可以看出，虽然第6组数据对应的模型的召回率只有0.878，精确率和F1值也只有0.969和0.921，出现这种情况可能是因为该组数据的测试集中存在个别的标记错误。但是从整体上看，大部分组的精确率、召回率和F1值都在0.95到0.99左右，处于一个范围较小的区间内，平均指标中最低的召回率也高达0.967，偏差也仅有0.038，F1值为0.973，偏差仅为0.024。但是在实际情况中，相似重复记录的占比较少，而召回率可以表示数据中没有相似重复记录的极端情况，所以WE-CNN模型在极端情况下的平均识别率也能高达0.967。因此，WE-CNN模型具有较高的识别率和较强的泛化能力。

基于WE-CNN模型改进的SIM-CNN模型的K折交叉验证的各项指标如表8所示。

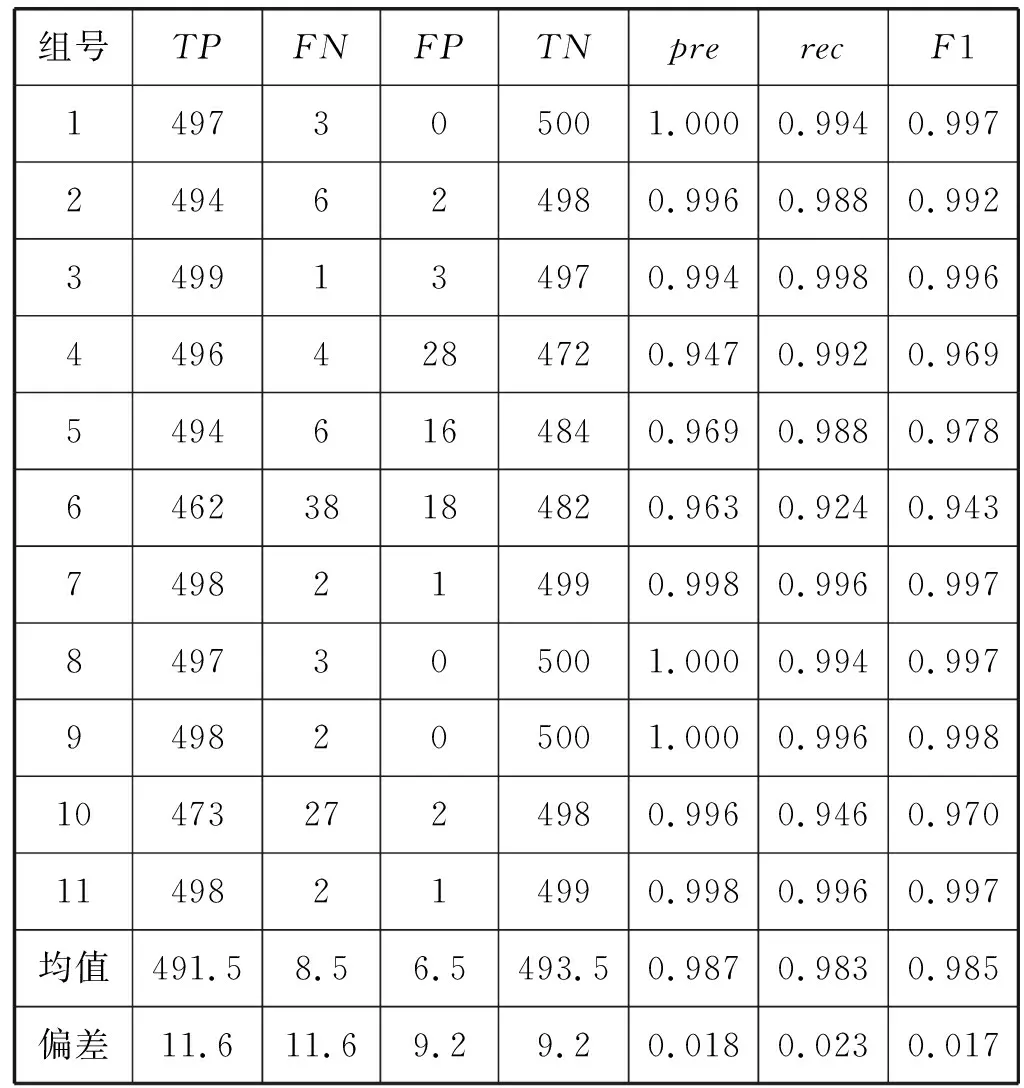
表8 SIM-CNN模型K折交叉验证各项指标

其中SIM-CNN模型的K折交叉验证实验的每一组的训练数据和测试数据都与WE-CNN模型K折交叉验证实验中对应的组中的数据相同。各类超参数也与WE-CNN模型的K折交叉验证实验相同。从表9中可以看出，SIM-CNN模型的各项指标要明显优于WE-CNN，整体上都有了一定的提升。同样是最低的第6组数据对应的模型的召回率已经达到了0.924，比SIM-CNN模型提升了0.046。从整体上来看，大部分的精确率、召回率、F1值都在0.97到1之间，处于一个很小的区间内，从平均上来看，精确率、召回率和F1值都达到了0.98以上，而偏差最大的召回率也仅有0.023，F1值也高达0.985，偏差仅有0.017。因此，与WE-CNN模型相比，SIM-CNN模型具有更高的识别率和更强的泛化能力。

(4) 运行时间。数据量为本次实验所用的11 000对记录，batch-size均设置为64，迭代次数epoch均设置为60，WE-CNN模型和SIM-CNN模型的训练数据和测试数据都相同。两模型的整体运行时间如表9所示。

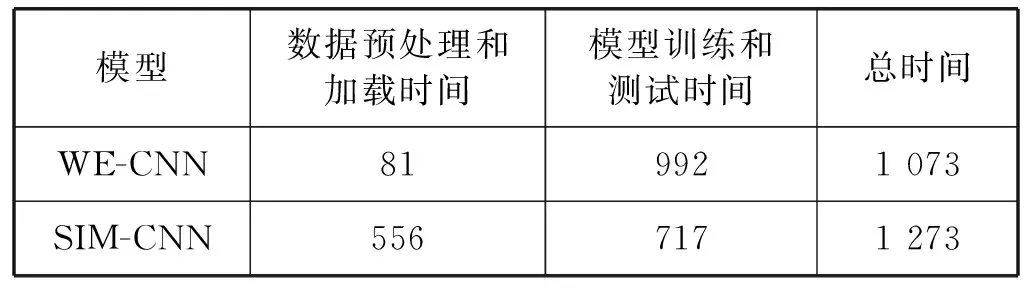
表9 模型运行时间 单位：s

从模型训练和测试时间上来看，SIM-CNN模型的训练速度要比WE-CNN模型快，但是由于SIM-CNN模型的输入是两条记录对应的相似度矩阵，生成实验所需的所有相似度矩阵需要556 s，而生成WE-CNN模型所需的所有词向量矩阵仅需81 s。因此从整体上看，在本次实验的数据集中，WE-CNN模型的整体运行时间为1 073 s，比SIM-CNN模型的整体运行时间少200 s。

(5) 模型对比。图8为相同的实验数据在WE-CNN、SIM-CNN和文献[10]所述的BP神经网络3种模型下的各项指标柱状图。

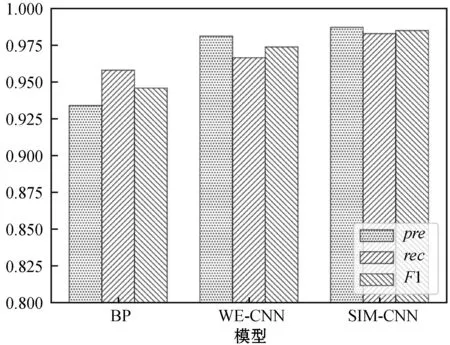
图8 3种模型指标对比

可以看出，在整体识别效果上SIM-CNN模型最好，其次是WE-CNN模型，最后是BP神经网络。这是因为SIM-CNN的输入为相似度矩阵，与WE-CNN的输入词向量矩阵相比，在都保留了原有信息的基础上输入更简洁，需要训练的参数更少，因此SIM-CNN模型的识别效果最优。而BP网络的输入是相同字段间的编辑距离值组成的向量，而安防数据中的部分相似重复记录的记录对相同字段间的编辑距离值较大，部分不是相似重复记录的记录对相同字段之间的编辑距离值较小，识别效果自然较差。

3.5 实验评价

综上所述，SIM-CNN模型在上述实验数据集中的识别率和在没有相似重复记录的极端情况下的识别率(实验数据集中的召回率)均优于WE-CNN模型，但是SIM-CNN模型的数据生成和加载时间较长，导致整个训练和测试的时间要长于WE-CNN模型。如果WE-CNN模型可以达到识别率的要求，或者检测时长受限，可以使用WE-CNN模型进行相似重复记录的检测。如果对识别率等指标要求较高，或者检测时长宽松，可以使用SIM-CNN模型进行相似重复记录的检测。

4 结 语

对于任意两条记录来说，相似重复记录检测只有是相似重复记录和不是相似重复记录两种情况，故本文将相似重复记录检测问题视为了二分类问题。同时考虑到安防行业数据的相似重复记录检测要比网络上的开源数据的检测难度高，并且需要较高的识别率和较强的泛化能力。因此引入了CNN检测相似重复记录，提出以词向量矩阵为输入的WE-CNN模型和以相似度矩阵为输入的SIM-CNN模型。

WE-CNN是以LeNet- 5为基础进行改进的，现将改进内容总结为以下三部分。

1) 输入和输出层：将输入层设置为两个60×100的词向量矩阵；输出层增加Sigmoid函数。

2) 输入和输出层以外各层：将S2层与C3层之间设置为全映射；C5层设置为全连层并改名为F5；C1和C3层的采用3×3的卷积核；S2和S4层均设置为最大池化；在各层之间加入Dropout方法。

3) 优化器和损失函数：使用Adam优化器对模型进行优化；使用交叉熵损失函数对模型的损失进行计算。

将改进后的模型(WE-CNN)应用于安防数据相似重复记录检测，通过K折交叉验证，得出了平均精确率、召回率和F1值均在0.96以上的结果。

SIM-CNN改进了WE-CNN的输入层，将一组词向量矩阵浓缩为一个相似度矩阵。在安防数据相似重复记录检测中，SIM-CNN模型K折交叉验证的平均精确率、召回率和F1值均在0.98以上。SIM-CNN模型在损失了数据预处理和生成的时间的同时，精确率、召回率和F1值相对于WE-CNN模型分别提高了0.612%、1.656%和1.131%，偏差相对降低了33.333%、39.474%和29.167%。

以上验证了两种模型都具有较高的稳定性和泛化能力，可以适用于安防数据相似重复记录检测。但是当前模型和模型生成的过程还存在需要进一步完善或者改进的问题，比如安防数据标记方法较难、安防数据中的相似重复记录的数量可能小于训练所需的相似重复记录的数量和安防数据相似重复记录清除算法的设计等问题还需要解决。