改进遗传算法在移动机器人路径规划中的应用研究

陈高远 宋云雪

(中国民航大学航空工程学院 天津 300300)

0 引 言

针对移动机器人的路径规划问题[1]，人们提出了不同方法，例如人工势场法[2-3]、Dijkstra算法[4-5]、快速扩展随机树算法(RRT)[6]、A*算法[7-8]、粒子群算法(PSO)[9]等。其中遗传算法(GA)最早是由John Holland基于生物进化原理提出的启发式搜索算法[10-11]，随着深入研究，因其灵活性以及与可扩展性等优势被广泛应用于路径规划问题。在遗传迭代过程中由于种群初始规模过小、选择和变异的不确定性等原因，会出现过早收敛仅仅得到局部最优，为此许多学者对遗传算法进行了改进。仪孝展[12]将模拟退火算法与遗传算法相结合，利用模拟退火算法可变的概率选择新解，并且能在较好的解空间进行搜索的特性，解决遗传算法迭代到一定次数后进化停滞问题。魏彤等[13]提出了相邻帧之间关联来平稳路径，通过上一帧的路径信息作为下一帧路径规划的参考，减少上下两帧的差异，有效地提高了行驶过程中的稳定。Xin等[14]提出了基于多域反演的遗传算法，利用多域反演增加后代数量的策略，并进行第二次适应性评价，以消除不需要的后代保留最有利的个体。这种方法增强搜索的能力和产生优秀个体的可能性。Nazarahari等[15]提出了多目标增强的遗传算法，在连续环境中从路径长度、平滑度和安全性方面寻找最优路径，该算法结合人工势场法并且对初始变异算子进行改进能够在连续的环境中找到可行的网格路径。宋宇等[16]将RRT算法与遗传算法相结合，用RRT算法产生初始路径，同时增加了插入算子，最后使用遗传算法来优化路径。Lee等[17]提出一种基于障碍物的搜索方法，来识别出与给定障碍物相邻的临界无碰撞点，同时，将遗传算法与目标点方向因子相结合来获取有效路径。

在对遗传算法的研究和对文献研究分析的基础上，考虑到遗传算法既可以用于单目标简单路径规划，也可以用于多目标复杂路径规划，并且具有较强的鲁棒性和与其他算法结合的可扩展性等优点，对遗传算法进行了改进，提出采用粒子群优化算法来重构变异算子，提高算法的速度，确定遗传算法进化的方向。在遗传迭代过程中，对适合度函数加入惩罚因子避免过早收敛，如果路径因与障碍物相交而不可行的，则对其适合度进行惩罚。同时为了解决由于交叉和突变产生大量的不可行路径，加入修复机制研究不可行路径，然后对其修复。

1 构型空间

1.1 地图构建

将地图定义为大小为n的正方形[0,n-1]2，使用规则间隔对其进行离散化，得到以下网格：

G={(i,j)|0≤i,j≤n-1}

(1)

地图中障碍物占有的网格occ∈Rn×n可以如下表示：

在单目标简单地形中表示为：

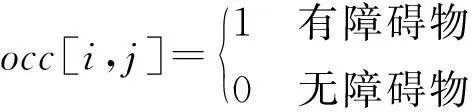
(2)

多目标复杂地形中表示为：

(3)

式中：f(xi)表示第i格的复杂度，可以用该位置的高度表示，并且对其进行归一化操作。

1.2 路径表示

针对文献[18]中采用的符号编码方式，本文采用二进制编码方式来表示路径，更方便地进行后续的交叉、变异等遗传操作。路径由n-1个对方向和距离动作描述，如表1所示。每个动作都会告诉机器人从当前单元格朝哪个方向移动，以及沿该方向经过了多少个单元格，该问题可以用2种不同类型的路径来表示：X单调路径：每个动作都会使路径的x坐标正好增加1。Y单调路径：每个动作都会使路径的y坐标正好增加1。这种方式能够在x轴上和y轴上分别执行n-1个操作之后到达最后一列或行如图1所示。

表1 路径动作编码

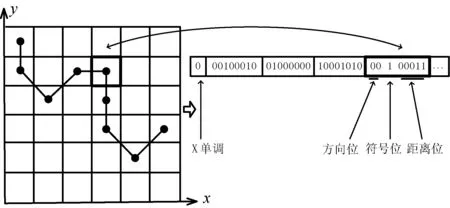
图1 路径的二进制表示

可以将路径存储为固定长度的二进制数组ε，该数组的长度为：

len(ε)=1+(n-1)×(2+1+log2(n))

(4)

其中二进制数组的第一位ε[0]=0时表示路径是X单调，ε[0]=1表示路径是Y单调，2+1+log2(n)代表每行或每列的方向和距离，前两位表示前进的方向，剩下的二进制位，如果方向为00，则表示将距离表示为有符号的整数，否则将被忽略随机填充。当X单调并且方向为00时，如果距离为正，路径向上移动，则沿副对角线右上角移至下一列，否则向下并沿主对角线右下角移动。当Y单调且方向为00时，如果距离为正，路径向下移动，然后沿副对角线向左下移至下一行，否则向右并沿主对角线右下移动。

2 改进遗传算法

2.1 初始化

初始化一个具有固定大小为p的路径个体种群S，其中的P-2个随机初始化，具体来说，它们的二进制表示形式是随机生成的，每个位在[0,1]之间进行均匀采样。最后两个路径分别是X单调和Y单调直线路径,路径个体种群S可以定义为：

S={l0,l1,…,lp-2,lx,ly}

(5)

式中：li表示随机生成的二进制路径；lx是X单调路径；ly是Y单调路径。对于多目标复杂地形来说，则需要初始化一个空的帕累托最优解集。

2.2 遗传操作

2.2.1 选择和交叉

锦标赛选择法[19]是一个根据适应度对比结果选择的过程，随机从种群中选择个体，这些个体之间相互竞争，适应度值高的个体获胜并被选择用于遗传算法的进一步处理。这种方法的优点是时间复杂度为ο(n)，相较于其他选择策略较低，易于并行实现，且不需要调整适应度参数。交叉的方式选择多点交叉。

2.2.2 适合度

当路径长度被最小化时，一个可行的路径的适合度可以如下表示：

f1(x)=n2-ncell

(6)

式中：ncell是指从开始到结束的过程中穿过的单元格的数量。如果路径因障碍物相交而不可行的，则对其适合度进行如下惩罚：

(7)

式中：ncoll是道路上与障碍物碰撞的次数。

这种碰撞惩罚允许根据碰撞次数和路径的长度对不可行的路径进行“分层”。最后，如果该路径不可行，因为它超出范围或未在最终单元格中结束，则该路径的适用性很低，为:

f1(x)=1

(8)

当复杂情况下来求解路径，需要再添加一个适应度函数：

(9)

对于不可行的路径同样加入惩罚因子：

(10)

2.2.3 粒子群变异算子

粒子优化算法的数学描述如下[20]：假设搜索空间的维数为D，粒子数为n，向量Si=(si,1,si,2,…,si,D)表示第i个粒子的位置，pBesti=(pi,1,pi,2,…,pi,D)是当前搜索到的粒子的最佳位置，这个粒子群的最佳位置表示为gBesti=(g1,g2,…,gD)，向量Vi=(vi,1,vi,2,…,vi,D)是第i个粒子的位置变化率，每个粒子都会根据式(12)更新其位置。

vi,d(t+1)=w×vi,d(t)+c1×r1()×

[pi,d(t)-si,d(t)]+c2×

r2()×[gi(t)-si,d(t)]

(11)

(12)

式中：t为进化的代数；c1和c2是加速度系数参数，用来控制粒子做最大的步进；r1()和r2()是随机函数，其范围为[0,1]；w是惯性权重。

本文将粒子群方法用于变异算子的改进，首先，将种群划分为n个大小不同的子种群，迭代了k次之后，则种群可以表示为Pk={xk,1,xk,2,…,xk,n}，根据式(11)和式(12)对变异算子进行了重构，重构粒子群公式来作为变异算子，形式如下：

Δxmax,i(k+1)=Δxmax,i(k)+

c1×r1()×(xmax,i-xk,i)+

c2×r2()×(Xmax,i-xk,i)

(13)

xk+1,i=xk,i+Δxmax,i(k+1)

(14)

按式(15)来求解xmax,i的累计差。

Δxmax,i(k-1)+

(15)

式中：粒子群算法中的si,d由xk,n代替；pi,d由Pk中第i个子种群上的历史最优xmax,i来替换；gi由整个子种群的历史最优Xmax,i来替换；vi,d由Δxmax,i来替换；Δxmax,i是xmax,i的累计差的算术平均值。式(13)用来预测变异的方向和幅度，在突变之前进行预测，可以克服传统遗传算法中突变算子的随机性和盲目性，有效地提高种群中个体对进化环境的适应性，避免过早收敛。在式(14)中则表示进行变异操作。

2.2.4 修复过程

经过交叉和突变步骤后，会产生大量的不可行路径。因此，根据图2描述的修复机制，尝试将不可行的路径修复为一条可行的路径。

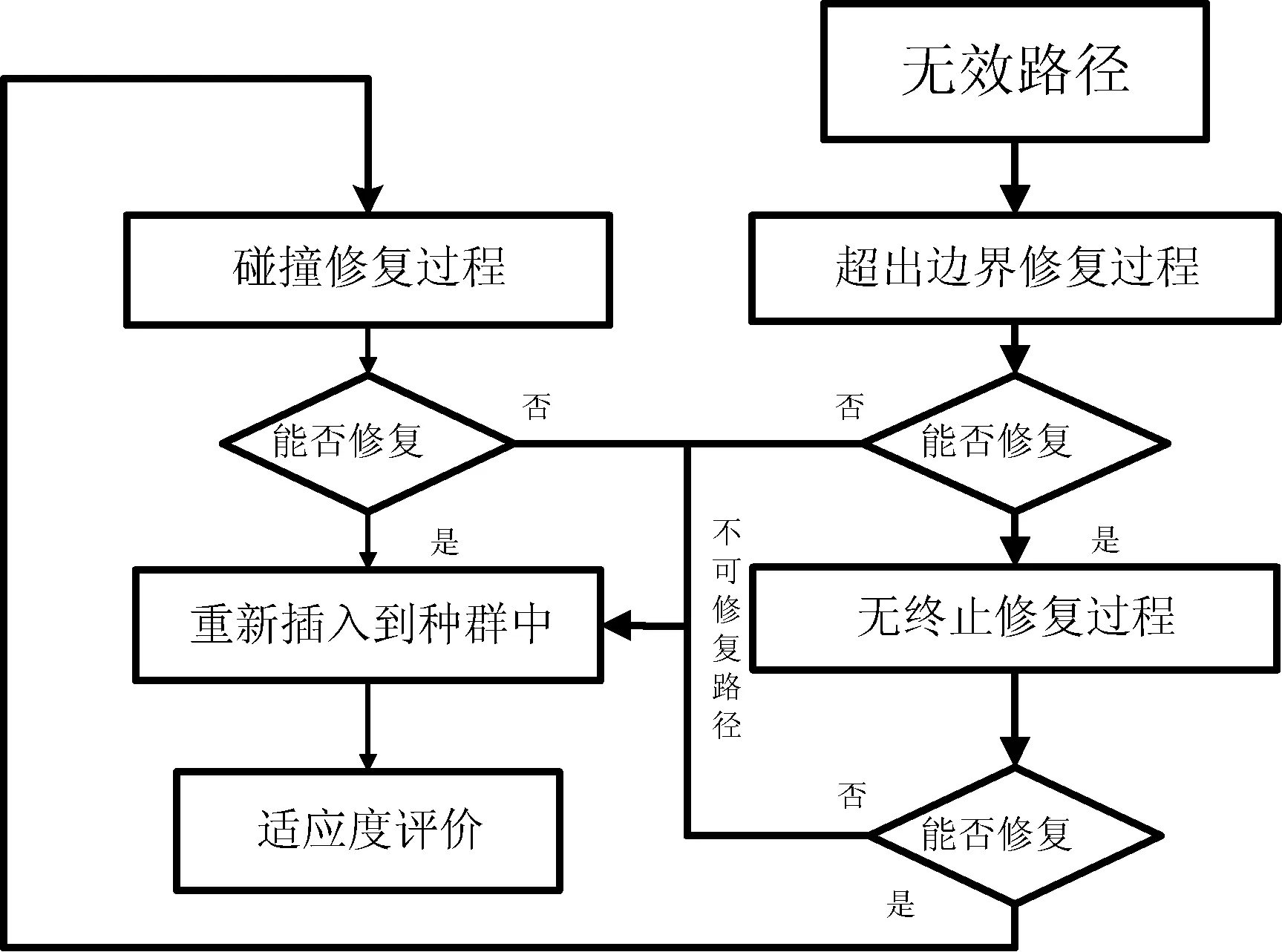
图2 修复机制遗传算法流程

该过程的详细描述如下：修复机制研究迭代过程中的所有不可行路径，并确定其无效的原因。首先，判断是否是“越界”修复，因为这个过程可能导致“未终止”和“碰撞”问题。然后判断“未终止”的问题，这个过程可能导致新的碰撞冲突。最后，判断路径上的碰撞。不是所有的路径都能完全修复，不可行的路径加入惩罚因子被重新注入新的种群中，以保持一个固定的规模的种群。(1) 越界修复，导致出界的操作分别被X单调路径和Y单调路径的一个水平或垂直步骤所替代。(2) 非终止修复，最后一个操作被更改，以便路径在结束单元格处结束。修复过程分别填充X单调路径和Y单调路径的最后一列或最后一行中的剩余单元格，以关闭该路径。(3) 碰撞修复，从开始的单元格开始，修复过程中尝试通过更改先前的操作来避免碰撞。然后更改下一个动作，以填充丢失的单元格并与路径的其余部分重新连接，重建路径并检查是否有新的碰撞。(4) 修复过程会在碰撞过程中反复进行，直到所有碰撞都可以避免或无法修复为止。

3 仿真结果

3.1 单目标简单环境

为了验证本文改进方法的可行性和有效性，对该改进遗传方法进行了仿真实验，经过50次迭代的路径效果以及最优路径长度与平均路径长度随迭代变化如图3和图4所示。

图3 “20×20”地图

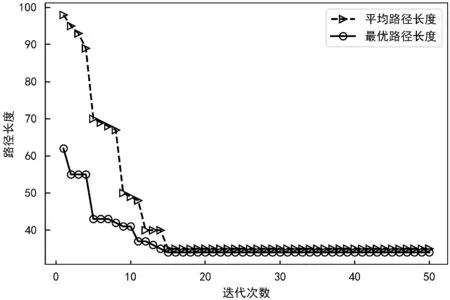
图4 路径长度变化

为了评估改进的遗传算法性能，将其与传统遗传算法、文献[16]、文献[17]进行对比。传统遗传算法在每一代根据适应度均匀采样一个新的个体种群, 因此效果不好。本文算法与传统遗传算法、文献[16]初始种群均为100，根据文献[17]描述选择初始种群为60,并对它们都进行100次的迭代。如图5和图6所示，在这些地图上，绘制出了本文改进遗传算法、传统遗传算法、文献[16]、文献[17]寻找的路径。

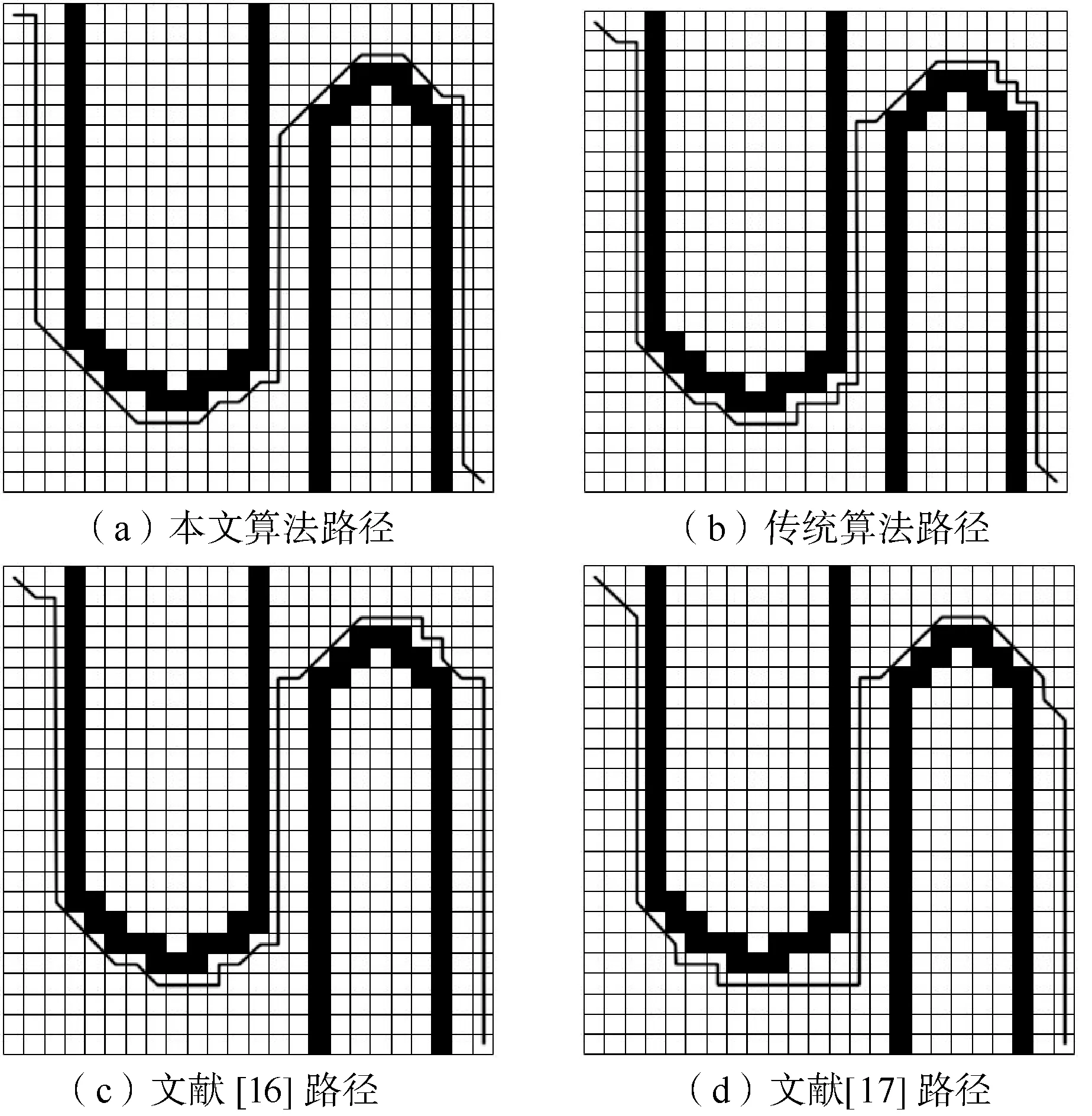
图5 “窄谷”地图

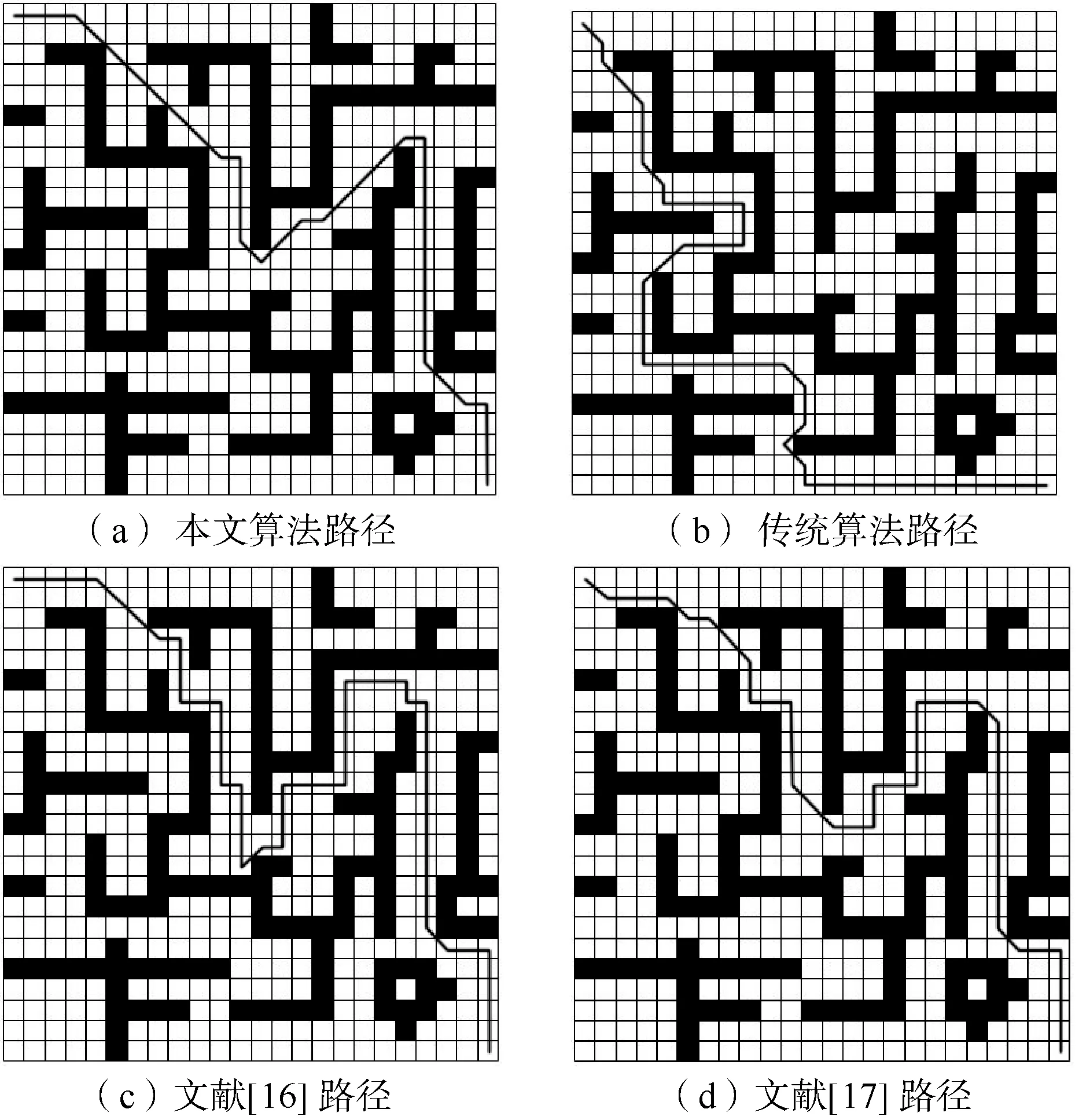
图6 “迷宫”地图

结果是对100次运行的结果取平均值，并汇总在表2中。

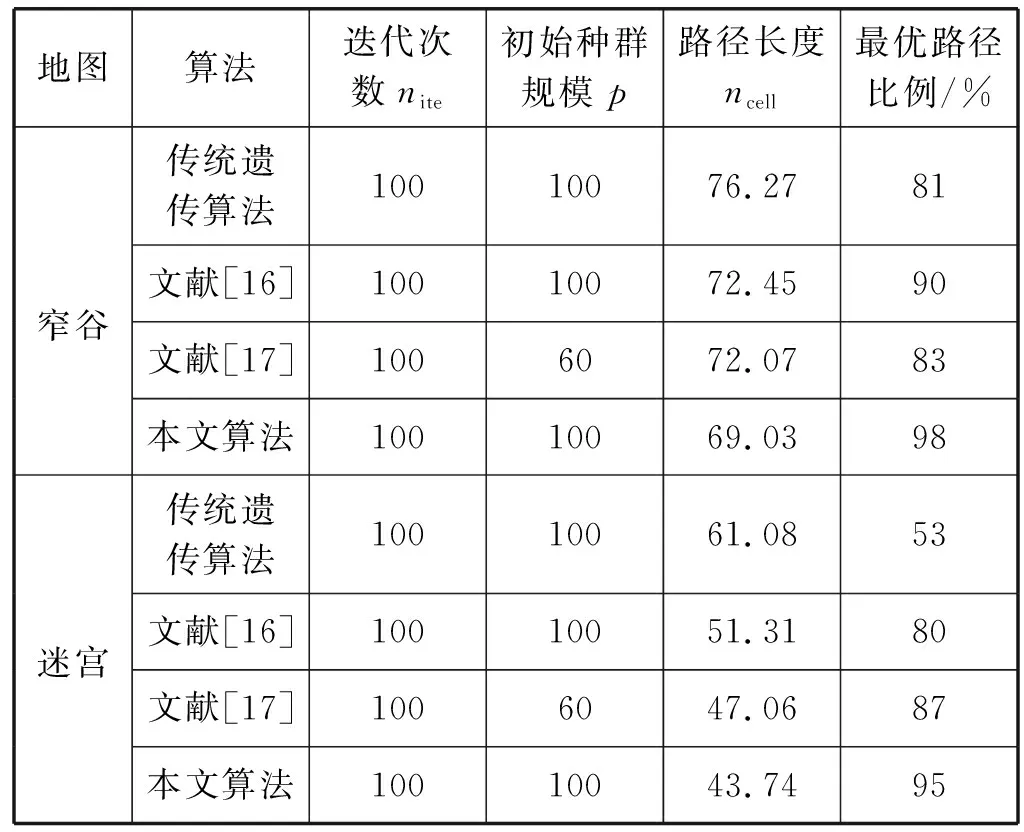
表2 算法在不同地图的比较

对于“窄谷”和“迷宫”图，图7和图8分别显示了传统遗传算法、文献[16]算法、文献[17]和本文算法相对于迭代数的最佳路径长度的演变。

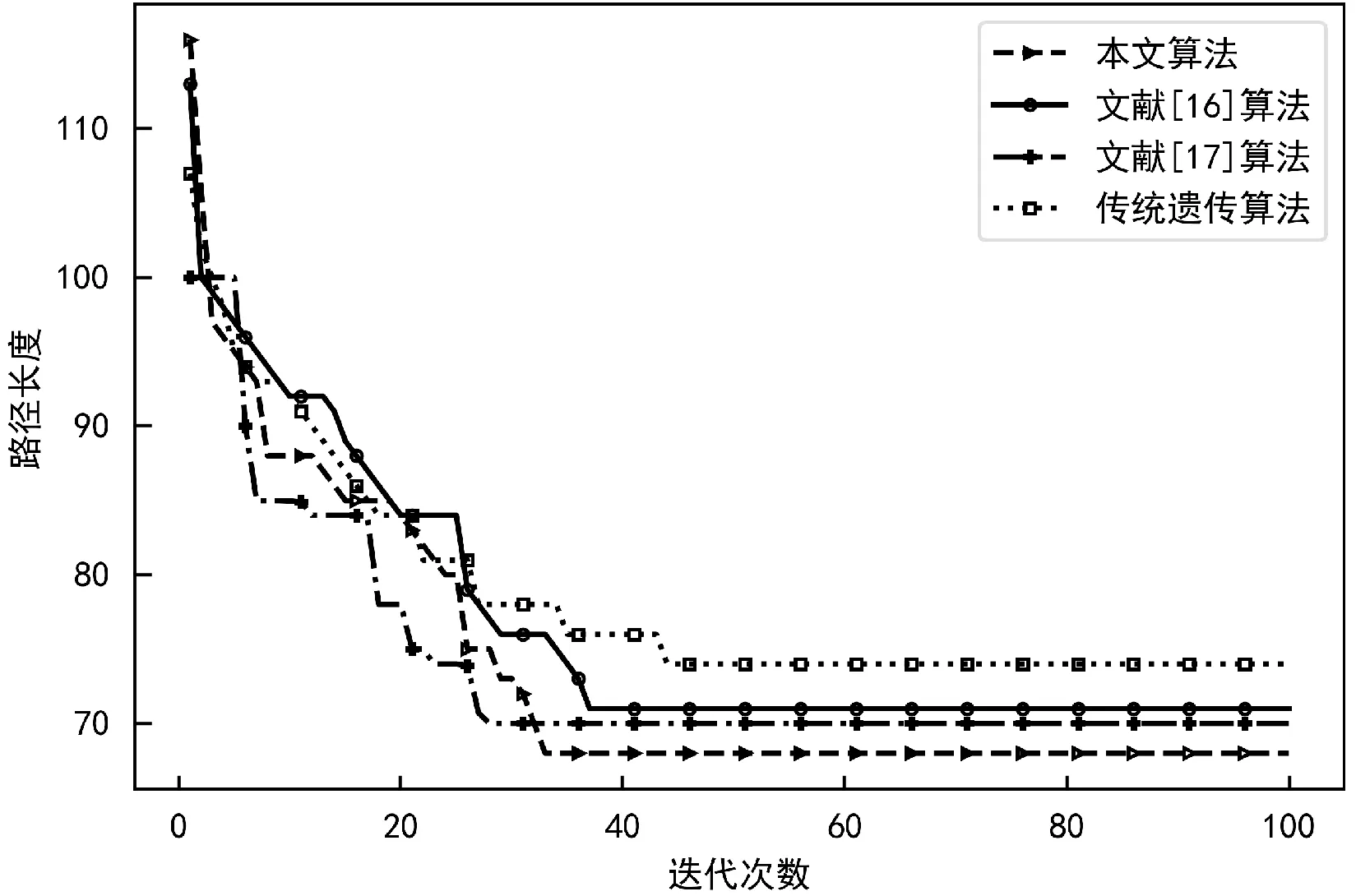
图7 “窄谷”地图路径长度变化

图8 “迷宫”地图路径长度变化

可以看出，本文改进遗传算法在寻找可行路径方面性能更好。在图7中，它需要大约33代来找到一个可行的路径，比传统遗传算法更快地缩短了路径的长度，本文算法比传统遗传算法大约缩短了7个单元格，比文献[16]大约缩短了3个单元格，比文献[17]大约缩短了3个单元格。这在图8中更加清晰，对于更复杂的“迷宫”地图，即使经过100次随机种群初始化，传统遗传算法也很难找到一条最优可行的路径。文献[16]随着地图的复杂，因为RRT算法前期搜索路径，会耗费较长的时间；文献[17] 结合了目标点方向因子，加快了迭代速度，但因为初始种群规模过小以及迭代过程中种群多样性的降低，容易造成早熟收敛；本文算法通过粒子群变异算子以及加入惩罚因子避免了过早收敛，同时修复机制保证了迭代过程中种群多样性，所以路径寻优方面更具优势。在“迷宫”地图中，平均而言，改进遗传算法的可行路径比传统算法约短17个单元格，比文献[16]得到的路径约短了8个单元格，比文献[17]约短了4个单元格。

此外,从表2可以看出，改进的遗传算法的最优路径比例远高于传统遗传算法，并且相对于文献[16]和文献[17]在最优路径比例方面也要高，当地形变得复杂时，最优路径的比例越高，效果越好。

3.2 多目标复杂地形

对于矩阵的线性组合，最优控制算法只输出一个最优路径，而复杂地形给出了一组可以选择的帕累托最优路径。

在尺寸n=51的地图上测试了复杂地形，如图9所示。连续的地图展示了不同海拔高度的表面，以及不能交叉的山峰和低谷。为了在这个地图上运行改进的遗传算法，连续地图被预处理成一个2D占用网格，如图10所示。将山峰和孔洞转换为固体障碍物，然后将高度归一化调整为0到1之间。最后计算单元的难度为对应区域的平均高度。

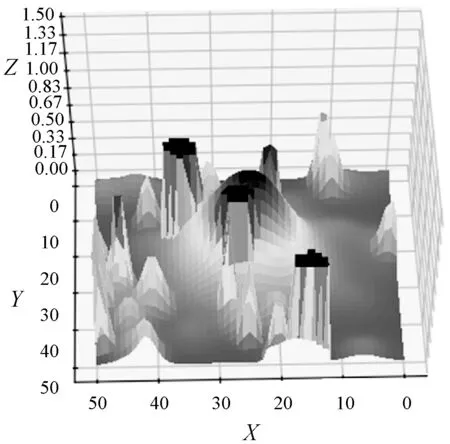
图9 连续3D地图

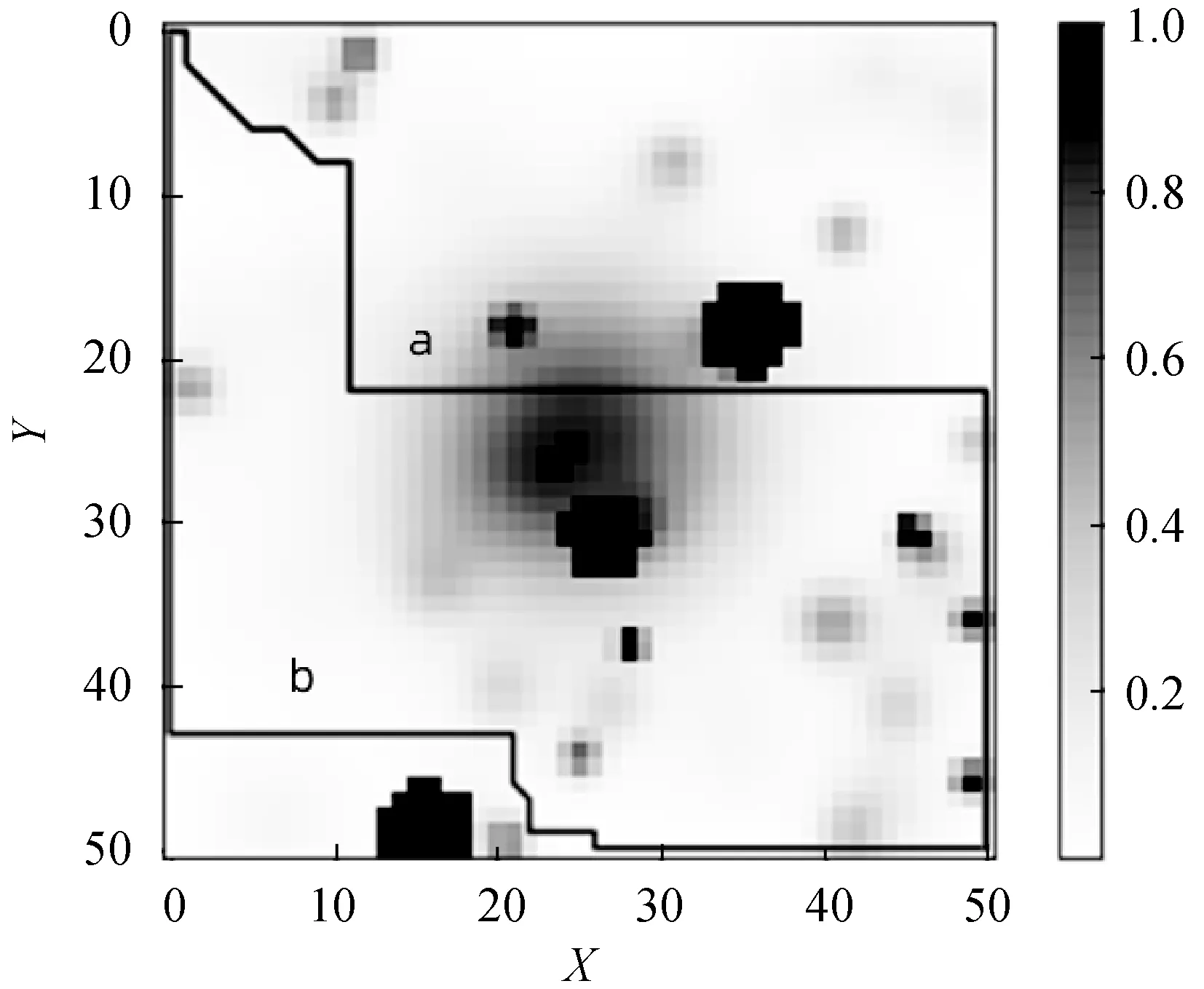
图10 2D占有网格

运行复杂地图之后，从帕累托最优解集中提取了两个特定路径，它们分别满足不同的目标，其中a路径长度为90，困难度为21.92。b路径长度为102，困难度为4.78。从图10可以看出通过改进遗传算法在多目标复杂环境下路径规划中可以获得不同的路径解。

4 结 语

综上，本文针对传统遗传算法中存在的问题，提出改进的遗传算法，算法考虑了单目标和多目标路径规划情况，经过仿真实验，证明了改进后的算法的可行性和有效性，综合来说本文具有以下特点：(1) 路径表示采用了二进制编码的方式，方便了后续的遗传操作，便于理解和实施。(2) 用粒子群优化算法重构变异算子，加大算法前期搜索有效解的数目，有利于提升遗传算法效率，避免局部最优。(3) 对适用性加入了惩罚因子，对每代个体根据适应度进行惩罚进一步提高全局搜索能力，避免陷入局部最优。(4) 加入修复机制，解决由于交叉和突变产生大量的不可行路径，维持种群的规模和多样性。(5) 对单目标和多目标路径规划都进行了描述，提高了算法的可扩展性。