弧形双箭头蜂窝面内压缩性能试验与仿真

亓昌 丁晨 刘海涛 江峰 陈上 杨姝†

（1. 大连理工大学 汽车工程学院/工业装备结构分析国家重点实验室，辽宁 大连 116024；2. 大连理工大学 宁波研究院，浙江 宁波 315016；3. 中国北方车辆研究所，北京 100072）

蜂窝材料是一种典型的仿生材料，其设计灵感来源于天然蜂巢，具有构造精巧、承载能力强、质量效率高等优点，尤其在抗冲击吸能方面优势显著。在现有的多种蜂窝结构中，具有双箭头、内凹多边形以及手性胞元的蜂窝材料表现出不同于传统六边形蜂窝的负泊松比（Negative Poisson’s Ratio，NPR）特性，具有特殊的工程应用价值。在外载荷下，NPR材料表现出不同于传统材料的独特变形模式：在外力拉伸作用下，材料会垂直于加载方向膨胀；相应地，在压缩载荷下，材料会向受载区集聚，使局部密度增大，从而获得更好的抗冲击吸能效果。上述特性使得NPR材料具有比传统材料更高的平面剪切应力、剪切模量、挤压阻力和断裂韧性［1-2］，应用前景十分广阔［3］。

近年来，围绕NPR 蜂窝的力学性能及工程应用，国内外开展了较多研究。例如，Qiu 等［4］对六边形手性蜂窝进行了尺寸和形状优化，使其在大变形下保持恒定的杨氏模量和泊松比，并通过实验揭示了有效弹性性质的不变性取决于柔性六边形手性蜂窝的非线性。Qi等［5］通过实验、理论分析和数值仿真揭示了四韧带手性蜂窝的面内压溃响应。张新春等［6］探讨了胞元结构参数对六韧带手性蜂窝抗冲击性能的影响。杨姝等［7］提出了四韧带手性蜂窝夹芯吸能式发动机罩，与六边形蜂窝相比，该发动机罩能更有效地减小行人头部碰撞损伤。Qi等［8］采用弧形边代替传统内凹（Re-Entrant，RE）蜂窝斜边，得到了内凹弧型（Re-Entrant Circular，REC）蜂窝；理论、实验和仿真研究均表明，与RE 蜂窝相比，REC蜂窝可在压溃过程中形成更多塑性铰，具有更高的比吸能。卢子兴等［9］基于组合星型蜂窝（Star-Shape Honeycomb，SSH）和双箭头蜂窝（Double-Arrow Honeycomb，DAH）结构，提出一种新型的星型-箭头蜂窝（Star-Arrowhead Honeycomb，SAH）材料，数值仿真表明，相对传统星型蜂窝，SAH的平台区更长，平台应力更高，其单位质量吸能也高于SSH；他们同时给出了SAH平台应力的经验计算公式。韩会龙等［10］对比研究了星型与正方形蜂窝的动力学性能，结果表明，星型NPR蜂窝的动力学性能不仅与冲击速度和相对密度相关，更取决于胞元结构；他们同时给出了星型蜂窝的密实应变和动态平台应力的经验公式。Gao等［11］研究了DAH在不同冲击速度下的变形模式，发现差异显著；此外，随着相对密度和冲击速度的提高，材料抗压强度显著提高。马芳武等［12］研究了DAH 在不同倾斜角度下的冲击力学响应，发现诱发稳定有序变形模式的合理倾角有利于冲击能量的吸收。Gu 等［13］采用实验和数值仿真相结合的方法，研究了DAH 在不同方向、不同载荷作用下的变形行为，结果表明，DAH 在x方向拉伸载荷下的NPR 效应比在y方向拉伸载荷下的更显著，且倾角越小拉伸效果越好。Gao 等［14］揭示了基于DAH 设计的汽车防撞箱中DAH 胞元数量与支撑边长细比对结构整体比吸能的影响。Chen等［15］制作了金属DAH 夹层结构，研究了其在空气爆炸作用下的动力学行为，结果表明，与增加芯壁厚度相比，在保证质量不变的情况下，减小水平距离对减小背板变形的作用更为显著。

文中以传统DAH 胞元构型为基础，通过对其斜边进行弧形化处理，得到一种新型的弧形双箭头蜂窝（Circular Double-Arrow Honeycomb，CDAH）材料。通过样件试验与数值仿真，对比了DAH 与CDAH 在面内准静态压缩载荷下的比吸能特性。在此基础上，利用数值仿真进一步探讨了CDAH在不同速度下的面内动态冲击响应。

1 CDAH材料建模

1.1 几何模型

传统DAH 材料的单胞构型如图1（a）所示。以之为基础，分别采用两个等半径圆弧形胞壁代替一个斜直胞壁，得到图1（b）所示的CDAH材料胞元。

图1 DAH与CDAH胞元的几何参数示意图Fig.1 Schematic diagrams of geometric parameters of DAH and CDAH cells

由图1 可知，DAH 胞元的关键几何参数为θ1、θ2、l1、l2、t。除此之外，CDAH 胞元参数还包括弧形半径r1、r2。为对比起见，规定具有4×4胞元的两种蜂窝材料样件的外廓尺寸相同，即高度h=100 mm，宽度W=130.75 mm，厚度b=10 mm。以此为基础，不失一般性地，选择各几何参数取值如下：

根据多孔材料理论，基于文献［16］中的方法，CDAH的相对密度可表达为

1.2 有限元模型

本研究采用有限元软件建立DAH 与CDAH 材料样件的几何与有限元模型，进而利用求解器求解，仿真获得两种样件的准静态压缩及冲击响应。选择24 号分段线性塑性材料模型（MAT_PIECEWISE_LINEAR_PLASTICIY），具体参数为：杨氏模量E=2 355 MPa，屈服强度σys=33 MPa，密度ρ=1.24 g/cm3，泊松比μ=0.3。采用壳单元划分网格，单元厚度与样件厚度一致，均为0.8 mm。厚度方向采用5个积分点。为避免穿透，单元间设置自动单面（AUTOMATIC_SINGLE_SURFACE）接触算法。

DAH 与CDAH 样件的有限元模型如图2 所示。在x和y轴方向均包含4个胞元，垂直纸面厚度b为10 mm。如前所述，两者外廓尺寸一致。DAH、CDAH 蜂窝样件的下底面均固定在刚性平面上，顶面受刚性墙沿y轴负方向压缩，速度恒定，采用RIGIDWALL_GEOMETRIC 建模。当压缩速度为5 m/s时，DAH 数值仿真的动能仅为内能的1.34%，表明动态效应较小，可以忽略不计，材料具有准静态压缩特性。因此，为缩短仿真求解时间，仿真压缩速度v设为5 m/s。为模拟试验工况，蜂窝与刚性墙间摩擦系数设为0.2。此外，为保证模型中样件处于平面应力状态，所有面外自由度约束为零。

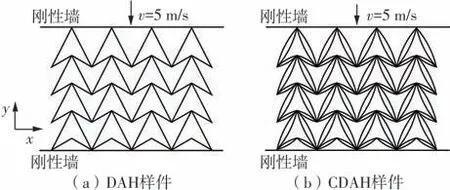
图2 DAH/CDAH样件的有限元模型Fig.2 Finite element models of DAH and CDAH samples

图3所示为采用不同单元尺寸仿真获得的DAH压缩应力-应变曲线。可以看出，随着单元尺寸减小，平台应力逐渐减小，且当单元尺寸为1.0 mm时应力基本收敛，即继续减小单元尺寸不再显著提高仿真精度，但会导致计算时间大大增加。因此，选用1.0 mm单元建模。

图3 有限元模型单元尺寸的压缩应力-应变曲线Fig.3 Compressive stress-strain curves of finite element model

2 准静态压缩试验与仿真模型验证

2.1 试验设置

为验证有限元建模方法的合理性和准确性，利用万能材料试验机对采用3D 打印技术制备的DAH和CDAH 样件分别进行了准静态压缩试验。3D 打印采用聚乳酸（Polylactic Acid，PLA）树脂材料，其力学性能参数与仿真模型一致。试验中将制备好的样件底面固定在万能试验机底座上，通过顶部刚性圆盘进行准静态压缩，加载速度设置为4 mm/min。通过与顶部刚性圆盘连接的力传感器测定压缩力，将压缩力除以压缩面积后换算得到压缩应力；采用高清摄像机记录样件的变形过程。

2.2 变形模式

图4 分别对比了当应变达到0.3 时DAH 与CDAH 样件的准静态压缩试验和数值仿真结果。可以看出，无论是DAH还是CDAH，在压缩载荷下均表现出明显的横向收缩变形，即呈现出一定的负泊松比效应。由于CDAH 对DAH 的斜直边进行了弧形化处理，在压缩过程中，结构关节处形成双塑性铰，提供了更好的支撑，故与DAH相比，CDAH的承载能力更强，平台应力也更高。此外，仿真得到的两种蜂窝变形模式与实际试验结果基本吻合，验证了仿真模型的有效性。

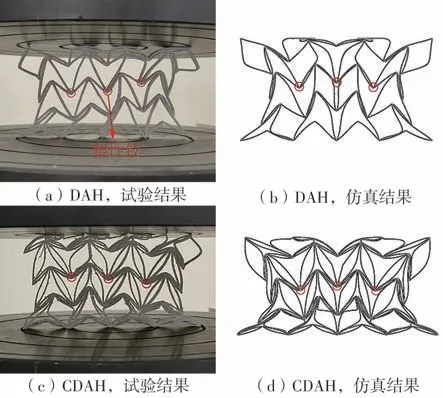
图4 压缩应变为0.3 时DAH、CDAH 的试验与仿真变形模式对比Fig.4 Comparison of experimental and simulated deformation modes between DAH and CDAH when the compressive strain is 0.3

图5所示为两种蜂窝的准静态压缩应力-应变曲线。可以看出，两种蜂窝均表现出明显的两阶段变形特点：阶段1表现为小应变下的近似线弹性变形，阶段2 表现为应力水平近似恒定的塑性大变形。CDAH 的试验与仿真结果最大误差为17.24%，进一步证明了仿真模型的准确性。需要说明的是，由于所制备的蜂窝样件胞元数相对较少（4×4），应力-应变曲线在平台段呈现一定波动；随着胞元数量增加，应力平台波动会相应减小，如后文所述。

图5 DAH、CDAH 蜂窝准静态压缩试验与仿真应力-应变曲线对比Fig.5 Comparison of experimental and simulated stress-strain curves between DAH and CDAH under quasi-static compression

2.3 比吸能对比

上述研究中，DAH 与CDAH 样件的基体材料、胞元和样件外廓尺寸以及胞元壁厚均相等，但样件总质量与材料相对密度不同。从轻量化设计角度，考虑重量因素，采用比吸能（Specific Energy Ab⁃sorption，SEA），即单位质量吸收的塑性变形能，对两种蜂窝的吸能特性进行对比分析。蜂窝材料的比吸能Em可由下式计算：

式中，Um为材料的总吸能量，σ为塑性应力，ε为塑性应变，m为材料的总质量，ρ*为多孔材料密度。

根据图5试验数据计算得到的DAH与CDAH样件比吸能随塑性应变的变化如图6 所示。可以看出，两种材料的比吸能均随应变增加而单调增大。由于胞元几何构型差异引起塑性能耗机制的不同，CDAH 的比吸能水平始终高于DAH。在应变达到0.6 时，CDAH 的平均SEA 比DAH 的高71%，充分说明CDAH 作为轻质性能材料，比传统的DAH 更具优势。

图6 DAH、CDAH的准静态压缩试验比吸能曲线对比Fig.6 Comparison of SEA curves obtained by quasi-static com⁃pression experiment between DAH and CDAH

3 CDAH动态压缩响应仿真分析

实际工程中，蜂窝材料更多地被应用于动态加载以至冲击工况。因此，有必要仿真分析不同加载速度下CDAH材料的动态压缩响应，为材料设计提供参考。

3.1 CDAH临界冲击速度

采用上述验证后的有限元建模方法建立具有12×12 个胞元的CDAH 动态压缩仿真模型，胞元尺寸如式（1）-（6）所列。基体材料选择7075-T6 铝合金，材料参数为：杨氏模量E=71.7 GPa，屈服强度σys=518.7 MPa，密度ρ=2.8 g/cm3，泊松比μ=0.33。谢灿军 等［17］的研 究 表明，7075-T6 铝合金在10、100及500 s-1这3种应变率下的动态力学特性无明显差别，故在建模中不考虑基材应变率的影响。单元类型、加载方式、接触设置等均与准静态压缩模型一致。

当冲击速度达到多孔材料的第1临界冲击速度vs1［18］时，开始形成局部变形，vs1可表示为

式中，εcr为应力达到第1次应力峰值时对应的名义应变，切线模量e（ε）可表示为

其中σ′（ε）为多孔材料线弹性阶段的弹性模量。

当冲击速度达到多孔材料的第2临界冲击速度vs2［18］（即冲击波速度）时，局部变形以冲击波形式进行传播，vs2可表示为

式中：σ0为多孔材料屈服强度；εd为材料压实应变，可通过能量吸收效率法确定［19］。多孔材料的吸能效率η（ε）可表示为

图7为具有12×12个胞元的CDAH样件的应力-应变曲线及对应的吸能效率曲线。根据式（9）-（10）得出第1 临界冲击速度vs1为14.7 m/s，即低于此加载速度时，材料中的冲击波效应不明显，多胞材料发生准静态变形。由式（13）得到该样件的εd为0.66，进而由式（11）得到材料的第2 临界冲击速度vs2为81.5 m/s。以大于该速度加载时，材料中的冲击波效应不可忽略，材料表现出动态响应吸能特性。

图7 CDAH的应力-应变和吸能效率-应变曲线Fig.7 Stress-strain and energy absorption efficiency-strain curves of CDAH

3.2 不同加载速度下CDAH 的动态压缩响应

参考CDAH 的第1、第2 临界冲击速度，分别选择5、20、50、100 m/s 的加载速度进行压缩过程仿真，研究、对比不同加载速度下CDAH的变形模式和动态响应。

图8所示为5 m/s压缩速度下CDAH的宏观变形模式。当压缩应变为0.1 时，CDAH 开始发生整体变形，蜂窝两侧向内收缩，呈现明显的负泊松比效应。应变达到0.2时，除整体收缩外，顶层胞元产生明显变形。当应变达到0.4 时，除中部胞元外，靠近上下刚性墙的胞元均产生大变形，弧形边完全坍塌。此外可发现，蜂窝左右两侧呈现不对称变形带。相比右侧胞元，左侧胞元变形更明显。这主要是由压缩过程中胞元薄壁屈曲过程的随机性造成的。当宏观应变达到0.6时，左右两侧胞元均发生较明显的变形，不对称现象消失，同时蜂窝下方部分胞元已被完全压实。

图8 冲击速度为5 m/s时CDAH的变形模式Fig.8 Deformation modes of CDAH at an impact velocity of 5 m/s

由图9 可以看出，当冲击速度由5 m/s 增至20 m/s 时，CDAH 的变形模式未发生本质变化。但由于刚性墙冲击加载率提高，材料不再发生图8（c）所示的由随机性导致的不对称变形，而是两侧同步收缩，同时顶部中间两个胞元快速下移，外侧弧形边则快速打开，且在应变达到0.2时顶层未发生坍塌现象，变形集中在次顶层胞元当中，形成局部倒“V”形变形带。随着宏观应变逐渐增大到0.4，顶部与底部蜂窝胞元快速塌陷、内凹。在此过程中，中间列胞元经历了收缩与膨胀的反复波动过程，直至应变达到0.6左右时开始塌陷、收缩，最后被完全压实。

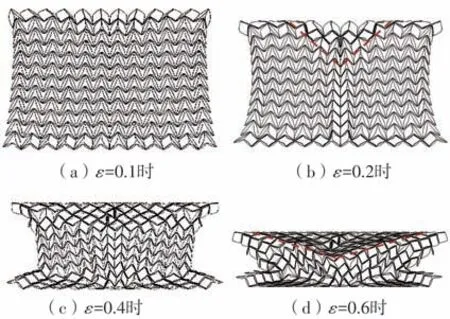
图9 冲击速度为20 m/s时CDAH的变形模式Fig.9 Deformation modes of CDAH at an impact velocity of 20 m/s

与上述结果不同，当冲击速度v=50 m/s 时，即远高于第1临界速度（14.7 m/s）并接近第2临界速度（81.5 m/s）时，CDAH 的变形模式由于冲击波效应而发生显著变化，如图10 所示。在材料宏观应变由零逐渐增大到0.2 的过程中，顶部胞元率先变形，但底部胞元由于惯性效应而呈现迟滞变形，从而在材料中形成明显的冲击波面。率先变形的胞元外弧边快速扩张，不再发生单个胞元倾斜后整体扁平的变形。在逐层变形带动下，侧胞元发生同样的变形，内弧边逐渐收缩，使得样件整体变形模式由倒“V”形演变为明显的倒“U”形。应变量进一步增大后，材料整体颈缩明显。相较于低速冲击，中间胞元的弧形边扩张数量增多，可吸收更多的冲击能量。当应变达到0.6时，上下边完全塌陷，中间胞元压实速度明显高于两侧，负泊松比效应明显。随着冲击速度进一步增大到100 m/s，惯性效应进一步展现，顶层胞元快速塌陷、压实，倒“U”现象减弱（尽管在高速冲击下，材料整体上仍能呈现出明显的颈缩现象），如图11所示。

图10 冲击速度为50 m/s时CDAH的变形模式Fig.10 Deformation modes of CDAH at an impact velocity of 50 m/s

图11 冲击速度为100 m/s时CDAH的变形模式Fig.11 Deformation modes of CDAH at an impact velocity of 100 m/s

图12给出了不同冲击速度下CDAH 的应力—应变曲线。可以看出，1 m/s 和5 m/s 冲击速度下材料的平台应力相差较小，接近准静态加载性能，这同时验证了前述计算得到的第1临界冲击速度值。而随着冲击速度的提高，CDAH 的平台应力显著增大，材料呈现明显的应变率效应。其原因一方面在于高速冲击下基体材料的惯性效应，另一方面与CDAH 胞元中的圆弧形薄壁在不同加载速度下的动态变形模式有明显关系。高速冲击下，CDAH 的平台应力远高于低速加载平台应力。本例中，CDAH样件在100 m/s 下的平台应力为9.93 MPa，是5 m/s下平台应力（3.31 MPa）的3 倍，说明CDAH 在高速加载下有更强的抗冲击性能。图13 中对比了不同冲击速度下CDAH样件比吸能特性随宏观应变的变化，发现随着冲击速度的提高，材料的吸能水平相应提高，有利于高速冲击载荷下的抗冲击防护应用。图14 所示为CDAH 在不同冲击速度下的泊松比变化情况。此处泊松比定义为蜂窝平均横向应变与整体压缩应变的负比值。当冲击速度大于5 m/s时，CDAH 在任何应变下都表现为NPR，且泊松比随应变变化而不同。泊松比在小应变时先下降到谷值，这意味着更明显的NPR特性。一般情况下，冲击速度越高，泊松比越大，NPR特性越不明显。

图12 不同冲击速度下CDAH的应力-应变曲线Fig.12 Stress-strain curves of CDAH under different impact velocities

图13 不同冲击速度下CDAH的比吸能曲线Fig.13 Specific energy absorption curves of CDAH under different impact velocities

图14 不同冲击速度下CDAH的泊松比曲线Fig.14 Poisson’s ratios of CDAH under different impact ve⁃locities

4 结论

文中通过对传统DAH 的斜边进行弧形化处理，提出了一种新型弧形双箭头蜂窝（CDAH）。通过数值仿真与试验，对比了CDAH 与DAH 的吸能效果，并对CDAH的动态冲击响应进行了数值分析，得出如下结论：

（1）在准静态压缩下对DAH 进行四边弧形化处理可以提高整体蜂窝的平台应力，使其比吸能提高；

（2）CDAH 在低、中、高速面内冲击下表现出不同的变形模式与力学性能，低速冲击下CDAH没有明显的变形带，整体呈现不规则的变形；

（3）随着冲击速度的提高，CDAH 的变形带从倒“V”形逐步过渡到倒“U”形，其平台应力与吸能量都有明显提升，且不同速度冲击下的CDAH都展现出明显的负泊松比特性。