考虑时延的网联车混合交通流基本图模型

罗瑞发 郝慧君 徐桃让 顾秋凡

（1. 同济大学 道路与交通工程教育部重点实验室，上海 201804；2. 西南交通大学 交通运输与物流学院，四川 成都 610031）

随着国家政策对智能汽车发展的推动，智能网联汽车日益推广和普及。最近的研究表明［1］，到2050 年，智能车辆占所有车辆的比例将达到75%左右。因此，在未来很长一段时间内，道路交通流量将包括人工驾驶车辆（Human-Driven Vehicles，HDVs）和智能网联车辆（Connected and Automated Vehicles，CAVs），交通流将从由一种车辆组成的同质流向由至少两种车辆组成的混合交通流过渡［2-3］。

在对智能网联车混合交通流基本图的研究中，Talebpour等［4］创建了跟驰模型来对人工车辆、联网车辆（联网后的人工车辆）和自动驾驶车辆的交通行为进行研究，发现随着联网车辆和自动驾驶车辆比例的增加，混合交通流基本图中的最大流量逐渐增大。Ye等［5］首先建立了双车道元胞自动机模型，然后通过仿真得到了不同比例下混合交通流的流量—密度关系图，发现随着智能网联车比例的增加，道路的通行能力显著增强。Zhou等［6］考虑智能网联车跟驰人工驾驶车辆时车头时距的差异，发现增大智能网联车的比例能减小基本图中流量—密度散点的分散。秦严严等［7］使用不同的跟驰模型对不同类型的车辆进行模拟，并利用平衡状态下车流的平均车头间距推导出了混合交通流的基本图模型，发现智能网联车渗透率以及自由流速度都对混合交通流的通行能力有积极影响。常鑫等［8］对交通流中的车辆类型进行了划分，进一步通过求交通流的平均车头间距得到了基本图，发现智能网联车渗透率和车队规模对交通流通行能力的提升均具有积极作用。综上所述，目前的部分研究对CAVs 的功能退化进行了单独考虑，但推导过程中未考虑不同车辆在应对前车突发情况时表现出的反应延迟。

有鉴于此，有学者在基本图的推导过程中考虑了时延［9-10］。Levin 等［9］建立了反映混合交通流通行能力和后退波速变化的元胞传输模型，但该模型并不能直观、量化地反映不同车辆比例对混合交通流通行能力的影响，且没有考虑CAVs 功能的退化。徐桃让等［10］从安全车头间距的角度出发，考虑不同车辆应对突发情况时的反应延迟，同时考虑CAVs车辆跟驰HDVs 时的功能退化，推导出了混合交通流的基本图模型，发现车辆时延对交通流通行能力具有显著的消极影响。

分析以上研究可知，目前鲜有文献同时考虑车辆功能退化和车辆时延［10］。本研究在基本图推导过程中同时考虑上述因素，以期使基本图模型能更加精准地反映流量、密度、速度之间的关系。

1 跟驰模型与车辆时延

1.1 车辆跟驰模式

对于同时存在智能网联车和人工驾驶车的混合交通流，若设CAV 渗透率为p，则HDV 占比为1 -p。由于不同类型车辆的相对位置随机分布，故存在如下4种跟驰情形。

①智能网联车跟驰智能网联车

在此情形下，后车与前车均为智能网联车，后车可通过车车通信获取前车的位置、速度以及加速度。此情形下后车的时延为车车通信过程中存在的延误，由于车车通信可实现前后两车状态的实时交流和同步行驶，因此延误可按0处理。由于CAV占比为p，理论上，此种跟驰模式所占比例为p2。

②智能网联车跟驰人工驾驶车

在此情形下，后车为智能网联车，前车为人工驾驶车，因此后车无法与前车形成车车通信，无法实现信息的实时共享。后车作为智能网联车在功能上发生了一定的降级退化，时延为车载感应系统获取和传输信息所需要的时间，故该情形下后车的时延相比情形①更大。此种跟驰模式所占比例为p(1 -p)。

③人工驾驶车跟驰人工驾驶车

在此情形下，前后两车均为人工驾驶车，后车驾驶员只能通过自身的生理感知了解前车状态的改变，时延为驾驶员的反应时间，相较于车载设备感知需要更长的时间，因此，与情形③相比，此情形下后车的时延更长。此种跟驰模式所占比例为(1 -p)(1 -p)。

④人工驾驶车跟驰智能网联车

在此情形下，后车为人工驾驶车，前车为智能网联车，后车获取前车状态的方式与情形③一样，都需要经过感知、识别、判断等生理过程，因此其时延与情形③中相同。此种跟驰模式所占比例为(1 -p)p。

上述4种跟驰情形中，后车对前后两车速度差和车间距的时延大小关系为：情形① < 情形② < 情形③ = 情形④。从车辆时延和跟驰行为上划分，共存在3 种不同类型的车辆——功能完全的CAVs、功能降级退化后的CAVs（Degraded-CAVs，记为DCAVs）以及HDVs。

1.2 车辆跟驰模型

对于CAVs，实车试验表明［11］CACC 模型可以较好地表现CACC 技术控制下的CAVs 跟驰特性，因此文中采用CACC 模型模拟情形①中CAVs 的跟驰行为，期望加速度f cn的控制公式为

式中：基于实车测试［11］对CACC 模型的标定，控制系数kp、kd分别取值0.45 和0.25；l为车身长，取5 m；sc0n为CAVs的最小安全间距，取2 m；速度更新间隔Δt取0.01 s；tcn为CAVs的期望车间时距，取接受比例最高的车间时距，即0.6 s。

参考文献［7］，对功能退化后形成的DCAVs，采用PATH 实验室标定的基于期望车间时距的ACC模型，该模型得到的仿真结果较符合实际测得的数据，可较好地模拟ACC车辆的跟驰行为，则期望加速度f an的控制公式为

式中：控制系数k1、k2分别取0.23 s-2和0.07 s-1；sa0n为DCAV的最小安全间距，取2 m；tan为DCAV期望的恒定车间时距，即与前车经过同一地点期望的时间差，根据PATH 实车调查结果［12］，取接受比例最高的车间时距，即1.1 s。

对于人工驾驶车，目前研究［13］多采用IDM 模型，该模型物理意义较为清晰，应用较为广泛。因此，文中采用IDM 模型对混合交通流中人工驾驶车的跟驰行为进行模拟，此时期望加速度f hn的公式为

式中：α为最大加速度，取2 m/s2；vf为自由流速度，取33.3 m/s；sh0n为最小安全间距，取2 m；β为期望减速度，取3 m/s2；Tn为安全车间时距，取1.5 s。

1.3 车辆时延

如前所述，在原有安全车头时距的基础上加上各自的时延，对3 类车辆所采用的跟驰模型进行改进。

对于人工驾驶车，使用τh表示其时延，改进后的跟驰模型如下：

对于智能网联车，使用τc表示其时延，改进后的跟驰模型如下：

对于退化后的智能网联车，使用τa表示其时延，改进后的跟驰模型如下：

参考文献［14］对不同车辆时延的取值，取人工车驾驶员的反应时间τh为0.4 s；智能网联车之间的通信时延很小，取τc为零；智能网联车跟驰人工车情形下，由于无法实现车车通信，故时延介于前述二者之间，取τa为0.2 s。

2 考虑多因素影响的基本图模型

2.1 基本图模型的推导

当交通流趋于稳定时，前后车辆速度差与最大加速度均为零［15］，因此，令式（4）—（6）中速度差以及加速度项等于零，得到CAVs、DCAVs 和HDVs的稳定车头间距如下：

式中，S1、S2、S3分别为CAVs、DCAVs、HDVs 的稳定车头间距，单位为m。

在混合交通流车队中，4 种跟驰模型下稳定车头间距的平均值可看作混合交通流的稳定车头间距［15］。设混合交通流总车辆数为N，当智能网联车比例（即渗透率）为p1时，混合交通流的稳定车头间距L可以表示为

根据车头间距与交通流密度之间的关系，可得交通流密度的公式如下：

将式（7）代入式（9），可得交通流密度与速度的关系如下：

结合流量、密度和速度之间的交通流关系式q=kv，可得流量和速度之间的关系如下：

根据式（10）和（11），可得到不同智能网联车比例p1下的混合交通流基本图，如图1所示。

由图1可知，随着智能网联车比例的提高，混合交通流的通行能力逐渐增大，说明智能网联车对于道路的通行能力有积极影响。当智能网联车比例为100%时，混合交通流的最大流量为4 436 辆/h，对应的最佳密度为37辆/km。

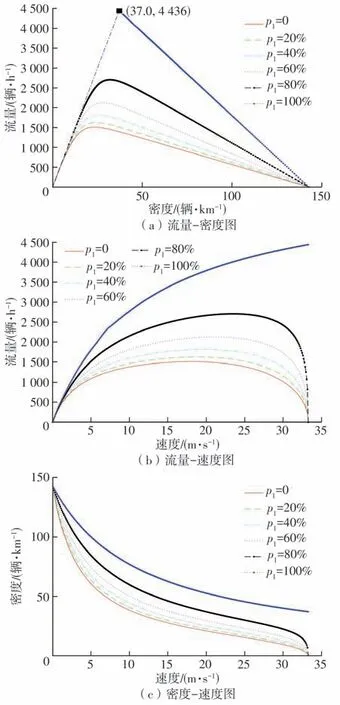
图1 不同p1下的交通流基本图Fig.1 Fundamental diagrams of traffic flow under different p1 values

2.2 参数敏感性分析

为进一步研究自由流速度对基本图的影响，在保持跟驰模型中其他参数不变的情况下，仅改变自由流速度v0，当自由流速度依次取15、20、25、30 m/s时，得到不同智能网联车渗透率对应的流量—密度关系，如图2所示。

图2表明，在每一种自由流速度下，混合交通流的通行能力随智能网联车比例提高而增大的基本规律不变。随自由流速度的增大，混合交通流的最佳密度逐渐减小，但对应的最大流量逐渐提高。当自由流速度分别为15、20、25、30 m/s 时，最佳密度分别约为62.4、52.7、45.5、40.0辆/km，对应的最大流量分别约为3 370、3 794、4 095、4 320 辆/h。综上所述，自由流速度对混合交通流的最大流量有积极影响，对最佳密度有消极影响。

图2 自由流速度的敏感性分析Fig.2 Sensitivity analysis of free-flow speed

3 仿真验证

3.1 仿真设置

为验证智能网联车渗透率以及车辆时延对交通流通行能力的影响，运用SUMO（Simulation of Ur⁃ban Mobility）软件对前文得到的理论基本图模型进行仿真。仿真路段为环路，总长度为10 km，路网设置如图3所示。

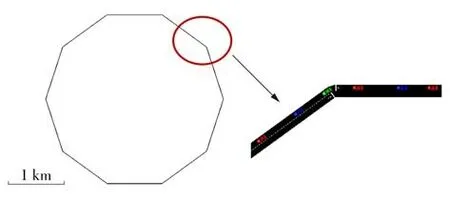
图3 仿真路网设置Fig.3 Setting of simulation road network

路段最大速度设为33.3 m/s，同时，为得到密度较大时的流量—密度散点，在仿真运行到一定时间时于指定路段进行降速干扰，将该路段上的车辆速度降至1 m/s。仿真总时长设置为18 000 s，即5 h，仿真步长为0.1 s。对每条路段（共10 条）进行数据检测，检测频率设置为120 s，即每隔2 min 检测一次路段的速度、密度等信息，流量由所得数据计算得出。

3.2 仿真结果及分析

3.2.1 智能网联车渗透率仿真结果及分析

为验证智能网联车渗透率对混合交通流流量的影响，取智能网联车渗透率分别为0、20%、40%、60%、80%和100%进行仿真，得到的交通流流量—密度基本图如图4所示。

图4 不同渗透率下的仿真结果Fig.4 Simulation results under different permeability

由图4可知，随着智能网联车渗透率的提高，仿真得到的最大流量不断增大，且仿真数据散点大致分散在理论曲线的两侧，与理论曲线的一致性较高（异常点主要在车流处于非平衡态和限速时产生），这证明了用理论模型处理渗透率的合理性和准确性。

3.2.2 车辆时延仿真结果及分析

为验证车辆时延对通行能力的影响，通过仿真获得了智能网联车渗透率为0时不同车辆时延对应的流量—密度散点关系图。与理论分析部分保持一致，当车辆时延分别取0、0.1、0.2、0.3 s 时（0.4 s 时与前述智能网联车渗透率为0 时的情形相同），仿真结果如图5所示。

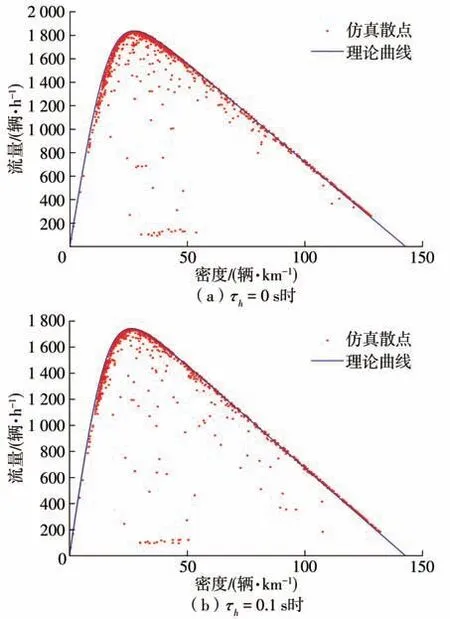
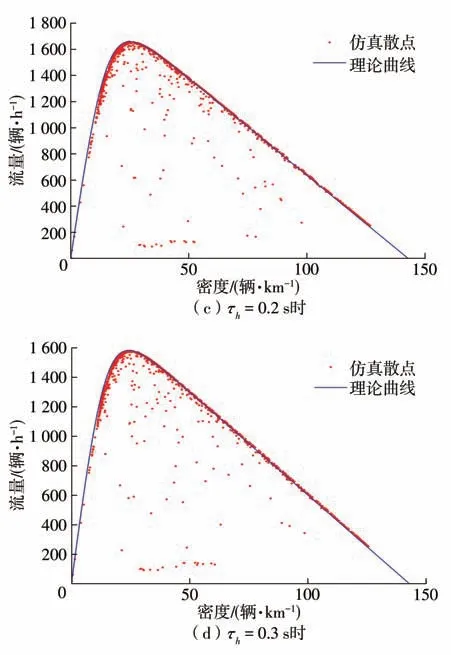
图5 不同车辆时延下的仿真结果Fig.5 Simulation results under different vehicle time delay

由图5可以看出，随着车辆时延的增大，仿真获得的最大流量逐渐降低，且车流在达到平衡状态后获得的流量—密度散点图均在对应的理论曲线的两侧，与理论曲线的一致性较高（异常点主要在车流处于非平衡态和限速时产生），这证明了用理论模型处理车辆时延的合理性和准确性。

4 结论

文中首先分析了混合交通流中智能网联车功能退化的情形，确定了车辆的种类和不同类型车辆的比例。然后，考虑车辆时延对安全车头时距的影响，对不同车辆跟驰情形下的安全车头时距进行了修正。在此基础上，通过求混合交通流的平均车头间距，推导得出了考虑智能网联车功能退化和不同类型车辆时延的基本图模型，弥补了已有研究未同时考虑二者的不足，并进一步通过参数敏感性分析得出以下结论：

1）智能网联车渗透率对混合交通流的最大流量具有积极的影响，随着智能网联车比例的增大，混合交通流的最大流量和最佳密度均逐渐增大；

2）自由流速度对混合交通流的最大流量具有积极的影响，随着自由流速度的增大，混合交通流的最大流量逐渐增大，但最佳密度逐渐减小；

3）车辆时延对混合交通流的最大流量具有消极的影响，随着车辆时延的增大，混合交通流的最大流量和最佳密度均逐渐减小。

文中同时考虑了车辆时延和车辆功能退化对基本图的影响，提高了流量—密度—速度基本图的准确性。在车辆时延方面，文中仅考虑了安全车头时距，未体现车辆对速度、速度差、位置差时延的差异，故后续研究可尝试采用合适的数学方法，将后车对速度、速度差、位置差的时延单独进行处理，从而提高模型的精确性。