考虑有轨电车效率的干线分段绿波协调优化模型
王昊 谢凝
(东南大学 江苏省城市智能交通重点实验室/现代城市交通技术协同创新中心/交通学院,江苏 南京 211189)
有轨电车作为一种中运量城市公共交通方式,近年来得到了迅速发展。有轨电车与享有专用道系统的地面公交在交通运行模式上具有相似性,具体表现在以下两个方面:①两者在路段上均具有独立路权;②两者在交叉口均与社会车辆共同受到交通信号控制。因此,优化有轨电车和公交的专用道系统在交叉口处的信号控制是提升通行效率的关键。干线绿波控制是常用的交叉口信号协调优化方法。
在干线绿波控制方面,Morgan 和Little 等[1-3]最早提出了半整数相位差信号协调方法,以绿波带宽最大为目标建立MAXBAND模型,通过分支定界法求解混合整数线性规划问题,确定干线交叉口的最优信号控制方案。Gartner 与Stamatiadis 等[4-7]在此基础上考虑不同路段间交通流量的差异,提出了带宽可变的MULTIBAND 模型,增大了模型的可行域。近年来,经典干线绿波设计方法被引入公交干线通行控制和有轨电车信号协调控制领域。戴光远[8]以干线交通系统的整体效益最大为优化目标,综合考虑干线信号协调控制下公交车辆绿波系统与社会车辆绿波系统的相互关系,构建城市干线公交绿波优化控制模型。然而,由于公交专用道在1个交通信号周期内可能有多辆公交车辆到达,若采用交通绿波控制,则实质上要求所有公交车辆均在绿波窗口内通过交叉口,导致公交车辆以队列形式停靠站点,并保持队列同步离开站点,这在实际公交调度与运行组织中难以实现。相比而言,有轨电车发车间隔较大,在1个信号周期内至多只有1列有轨电车通过交叉口,因而其更适合采用绿波通行控制。Jeong等[9-101]基于MAXBAND模型提出了有轨电车与社会车辆干线协调的TRAMBAND模型。王昊等[11]、孙国鼎[12]则提出了兼顾直行与转向有轨电车和社会车辆通行效率的多路径绿波控制模型,对各交叉口信号相序进行优化。上述模型均要求干线交叉口具有相同的信号周期,然而,由于干线交叉口空间规模与交通需求各不相同,现实世界中有轨电车沿线交叉口的信号周期往往难以统一,且有轨电车的路段行程时间受到道路交通状况、站点停靠时间的影响,与理想状态存在差异。因此,现有绿波设计方法在有轨电车的实际运行控制中难以获得预期效果。
实际应用中常采用信号优先控制提高有轨电车的通行效率。陈之惟[13]、杜建坤[14]分别提出了有轨电车感应式主动优先控制模型,并对有轨电车不同到达时刻的信号优先控制方式进行了分类讨论。然而,感应优先控制虽然提高了有轨电车的干线通行效率,但有轨电车通行相位的早启或延长减少了相交道路社会车辆的通行时间。当干线缺少信号协调方案时,交叉口频繁启动信号优先将对社会车辆的通行效益产生严重影响。
事实上,当有轨电车按照固定时间间隔发车时,其所需的绿波周期即为有轨电车的发车间隔。通常,平峰时段有轨电车的发车间隔不小于15 min,是交叉口信号周期的数倍。因此,有轨电车的绿波设计可以将发车间隔作为绿波周期对沿线交叉口的信号相位进行协调。通过有轨电车绿波的设计可以有效避免其在交叉口启动感应式主动优先控制,减少其对社会车辆的影响。而且,对于社会车辆而言,干线交叉口信号周期若存在差异,可采用分段式绿波的控制模式以适应不同交叉口的交通特性。
综上所述,干线有轨电车在运行组织方面存在不同于常规地面公交的特点,因而更适宜采用干线绿波控制方式。鉴于此,文中提出考虑有轨电车运行效率的干线分段绿波协调优化方法。根据交叉口特性对干线进行分段,形成面向社会车辆的干线分段绿波系统,克服单一绿波带无法适应干线交叉口信号周期不统一的缺陷。同时,协调有轨电车发车间隔与交叉口信号周期的关系,使有轨电车发车间隔为各分段绿波周期的倍数。对各分段绿波之间的信号相位差进行优化,形成以发车间隔为周期的面向有轨电车的绿波系统,在保障有轨电车交叉口通行优先权的同时,减少其对社会车辆绿波带的影响,从而兼顾有轨电车和社会车辆的通行效率,克服现有方法的缺陷。
1 干线交叉口信号周期与有轨电车站点位置协调优化
1.1 干线交叉口信号周期的协调方法
对干线交通进行绿波协调控制时,要求干线交叉口信号周期相同,而干线各交叉口交通情况存在差异,将信号周期完全统一后可能造成时空资源的浪费;另外,为提高有轨电车运行的稳定性与可靠性,保证各班次有轨电车在相同的信号相位到达交叉口,有轨电车沿线交叉口的信号周期与有轨电车的发车间隔需满足倍数关系,即
式中,T为有轨电车发车间隔,Ci为第i个交叉口的信号周期时长,pi为正整数。
有轨电车的发车间隔受其功能定位、客流需求的影响。根据《现代有轨电车交通工程技术标准》要求,平峰时段有轨电车的发车间隔通常不小于15 min,而交叉口信号周期不宜超过150 s。因此,在满足式(1)的前提下,根据干线交叉口的社会车辆流量,在有轨电车发车间隔的因子集合中选择交叉口信号周期并进行聚类,计算交叉口最优信号周期长度,并将其作为交叉口初始信号周期长度。比较交叉口初始信号周期长度与有轨电车发车间隔因子,将与初始信号周期长度差距最小的有轨电车发车间隔因子确定为交叉口信号周期,完成对交叉口信号周期的统一协调。
根据有轨电车发车间隔确定干线交叉口信号周期可以提升有轨电车交叉口优先通行的稳定性,减少启用感应式优先控制,降低其对社会车辆的影响;而且,对干线交叉口的信号周期进行协调,既有利于对干线交通的绿波协调控制,又可以适应干线不同交叉口的流量特点,避免道路资源的浪费或交叉口瓶颈的形成。
1.2 有轨电车站点位置对信号协调的影响
图1为有轨电车站点,图中示出了站点布设位置与交叉口位置的3 种关系。沿有轨电车行驶方向,布设在交叉口进口道附近的站点为近端式站点;沿有轨电车行驶方向,布设在交叉口出口道附近的站点为远端式站点;有轨电车站点布设在路段中部时为路中式站点。考虑乘客集散与道路几何条件,有轨电车站点多布设于交叉口附近,为近端式或远端式站点。若对向有轨电车共用同一站台,则近端式站点和远端式站点是相对而言的。

图1 有轨电车站点Fig.1 Tram stations
有轨电车在交叉口需减速或停车观察路况。将有轨电车站台设置为近端式站台,司机可以利用停站时间观察交叉口路况,并将有轨电车等待红灯的时间纳入停站时间中,减少停车次数。因此,在进行干线绿波协调时,对于有轨电车站点相对于行驶方向为近端式站点的情况,有轨电车交叉口信号优先控制不需要考虑该方向有轨电车通过交叉口的绿灯窗口,从而增大了绿波控制方案可行解的范围,减少了有轨电车优先控制对原有信号控制的影响。
2 分段绿波信号的协调控制优化模型
考虑到传统绿波模型在对干线进行协调优化时对不同绿波带间协调的局限性,文中结合有轨电车与社会车辆特性,以MULTIBAND 模型为基础,综合交叉口信号周期与有轨电车站点位置,建立了干线分段绿波信号协调优化模型,并使用混合整数线性规划算法进行求解。假设某干道共有n个交叉口,对文中模型变量进行定义,如表1所示。

表1 模型变量Table 1 Variables of the model
与传统模型相比,文中模型同时考虑了社会车辆和有轨电车在交叉口的通行效率,优化了信号控制方案和有轨电车停站时间,实现了有轨电车绿波与社会车辆绿波的协调;模型同时协调了分段绿波之间的相位差,以实现有轨电车绿波的连续性。
2.1 模型概述
干线信号协调控制优化模型分为社会车辆绿波系统约束和有轨电车绿波系统约束两部分,下面分别进行介绍。
相邻交叉口间社会车辆和有轨电车的绿波关系如图2 所示。图中,A、B、C、D为模型计算中社会车辆的参考点,A′、B′、C′、D′为模型计算中有轨电车的参考点,Si表示第i个交叉口。

图2 相邻交叉口间的绿波关系Fig.2 Green-wave relationship between adjacent intersections
2.2 社会车辆的绿波约束条件
以MULTIBAND 模型为基本约束,结合协调后干线交叉口信号周期对社会车辆的绿波带宽、相邻交叉口间的行驶时间关系及行程时间进行约束。
首先,对社会车辆绿波的方向不平衡性进行约束:
其次,使用0-1 变量uc,i来表示第i个交叉口与第i +1个交叉口之间的绿波是否打断——当信号周期相同、可以做绿波协调控制时,uc,i= 1;反之uc,i= 0。
对于可变带宽绿波系统,绿波带须处于相邻两个交叉口的绿灯时间范围内。当相邻交叉口不满足该条件时,uc,i= 0,使用无穷大整数M松弛该约束:
式(3)-(6)中,i= 1,2,…,n- 1。
根据图2,两个相邻交叉口之间的上行社会车辆从A点行驶到B点的时空轨迹满足如下约束条件:
式中,mi为上行方向在第i个交叉口处为保证等式成立的整数。
同理,对于下行社会车辆从C点行驶到D点的时空轨迹,可给出类似约束:
现实中,受不同路段长度以及车辆行驶速度限制,路段行程时间被限制在特定的区间内,社会车辆行程时间约束如下:
2.3 有轨电车绿波约束条件
根据图2,结合有轨电车的特性对MULTIBAND模型中的约束进行调整,建立有轨电车绿波系统的约束。在建立社会车辆绿波系统时,若相邻交叉口周期不统一,绿波被打断,相对相位差随周期不同而改变,则无需考虑两交叉口之间的协调关系;然而,对于有轨电车绿波系统,周期不同的相邻交叉口间仍存在有轨电车绿波,故仍需考虑两交叉口之间的相位协调关系。
图3对比了有轨电车与社会车辆通过交叉口的信号相位。可以看出,由于有轨电车的长度显著大于社会车辆的长度,且在交叉口的行驶速度小于社会车辆,因而其比社会车辆需要更长的交叉口清空时间。

图3 有轨电车和社会车辆的绿灯时间窗口Fig.3 Green time of tram and general traffic
对于有轨电车而言,首先应保证其在绿灯期间到达,且剩余社会车辆绿灯时间满足有轨电车通过交叉口的清空时间,这样才能确保有轨电车在社会车辆绿灯时间内通过交叉口,即
有轨电车绿波带宽为其路段行程时间提供波动空间。有轨电车通过交叉口的清空时间由有轨电车车长、交叉口尺寸及有轨电车通过交叉口的速度决定,用来保证有轨电车在冲突车流进入交叉口前可以安全通过交叉口,即
式中:Ltram为有轨电车长度;Lintersection,i为第i个交叉口有轨电车停止线到交叉口冲突点的距离;vintersection为有轨电车通过交叉口的速度,一般不大于20 km/h。
相较于社会车辆绿波系统,以有轨电车发车间隔为周期来描述两个交叉口之间有轨电车从A′点行驶到B′点的时空关系。对于布设有近端式有轨电车站点的交叉口,有轨电车可以利用停站时间等待通行相位,故可放宽其必须在绿灯时间内到达交叉口的约束;而对于没有近端式有轨电车站点的交叉口,与社会车辆类似,需要对有轨电车建立绿波系统基本约束,见式(14)。使用0-1 变量ul,i和uˉl,i对有轨电车站点位置进行表示,当站点为近端式站台时ul,i(uˉl,i) = 0;反之,ul,i(uˉl,i) = 1。
式中,mi,tram为有轨电车上行方向在第i个交叉口处为保证等式成立的整数。
同理,对于下行有轨电车从C′点到D′点,可给出类似约束:
对有轨电车的旅行时间进行约束,为不同路段有轨电车的行程时间设置相应的时间范围,需要满足:
式中,Li为第i个交叉口至第i+ 1个交叉口的距离。有轨电车在路段的行程时间由停站时间和路段匀速行驶时间组成,其中,路段匀速行驶时间考虑了站间距的影响,停站时间包括进出站点时的加速、减速时间,体现了站点客流需求以及上下客时间对行程时间的影响。由于有轨电车在运行过程中的速度较难控制,且过度控制可能会影响驾驶员操作,模型中假设有轨电车在路段匀速行驶的速度不变,通过调整停站时间实现有轨电车行程时间的优化。若将有轨电车速度设为优化变量,只需将其代入行程时间计算式(18)即可。
受天气状况、交通状况等影响,有轨电车在路段的行程时间存在不确定性,停站时间也会受到客流量等因素的影响。在保证满足最小停站时间的基础上,通过对有轨电车停站时间的调整,可以消除上述不确定性对有轨电车运行的影响,保证有轨电车运行的稳定性。
2.4 目标函数设计
由于受到发车频率的限制,通常1个信号周期内有轨电车的发车数量是有限的,无需追求过大的有轨电车绿波带宽。相对而言,社会车辆的通行需求更大,需要更大的绿波带宽。约束条件中已经满足了有轨电车通过交叉口的时间要求,因而在目标函数中只需对社会车辆的绿波带宽进行优化。文中将目标函数设置为社会车辆双向加权绿波带宽最大化,具体数学表达如下:
综合以上社会车辆绿波系统与有轨电车绿波系统的约束条件式(2)—(18)以及目标函数式(19),即为考虑有轨电车通行效率的干线分段绿波协调优化模型。该模型为混合整数线性规划问题,可使用分支定界法进行求解。
3 案例研究
3.1 案例简介
以南京市麒麟线有轨电车北湾营街至启迪大街段为研究对象,应用文中方法优化干线信号控制与有轨电车调度方案。
案例路段全长约3.06 km,包含天和路—北湾营街、天和路—天麒路、运粮河东路—天胜路、运粮河东路—南湾营街、运粮河东路—天兴路、运粮河东路—启迪大街6 个交叉口以及北湾营街站、天泉路站、南湾营街站、天兴路站、启迪大街站5个有轨电车站点。其中,天和路—北湾营街、天和路—天麒路和运粮河东路—天兴路为T形交叉口,其余3个交叉口为十字型交叉口。将由北向南方向定为上行方向,路段交叉口和站点分布情况如图4所示。平峰时段各交叉口进口道的机动车流量如表2所示。

图4 交叉口及站点位置Fig.4 Location of intersections and stations

表2 机动车流量Table 2 Flow of general traffic 辆/h
案例路段每个交叉口的信号控制方案如表3所示,相位时间包括4 s的黄灯时间。

表3 初始信号控制方案Table 3 Initial signal control scheme
根据案例路段交通状况,各路段社会车辆绿波车速优化范围设为[30,35] km/h,有轨电车运行速度为25 km/h。根据客流需求确定有轨电车停站时间限制,计算社会车辆和有轨电车的行程时间,如表4所示。为方便描述,将路段由北向南依次编号。

表4 车辆行程时间参数Table 4 Parameters of vehicles’ travel time s
根据式(13)计算各交叉口的有轨电车最小通过时间gtram,i,min,取最大值10 s为模型参数。根据实测数据,平峰时段南京麒麟线有轨电车的发车间隔为1 050 s,符合前文所述的平峰时段有轨电车发车间隔的要求。
3.2 案例分析
根据机动车流量重新计算交叉口最优信号周期并满足行人过街要求,与有轨电车发车间隔进行协调。有轨电车发车间隔1 050 s的因子中,大于100 s且小于150 s 的因子为105、117、131 s,将其确定为交叉口可选信号周期。根据流量计算出的最优信号周期选取大于且相差最小的因子为优化周期,将天和路—北湾营街、天和路—天麒路、运粮河东路—天胜路、运粮河东路—南湾营街交叉口的信号周期协调为117 s,运粮河东路—天兴路、运粮河东路—启迪大街交叉口的信号周期协调为105 s,则在运粮河东路—天兴路与运粮河东路—南湾营街交叉口之间社会车辆绿波将会打断,而有轨电车绿波连续。6 个交叉口中,运粮河东路—南湾营街、运粮河东路—天兴路、运粮河东路—启迪大街3个交叉口布设有上行方向近端式有轨电车站点,故不需要考虑上行有轨电车通行绿波;运粮河东路—天胜路、天和路—北湾营街两个交叉口布设有下行方向近端式有轨电车站点,故不需要考虑下行方向有轨电车通行绿波。若不考虑站点位置对绿波系统的约束松弛,该案例无解。
应用Python 软件对算例的优化模型进行计算,优化后,路段分为两段进行绿波协调,路段上下行绿波带宽及各交叉口信号控制方案如表5所示,车辆绿波轨迹如图5所示。

表5 优化后的信号控制方案Table 5 Signal control scheme after optimization s
分析表5 及图5 可见:优化后有轨电车在保持路段速度恒定的情况下,通过调整停站时间直接通过交叉口,避免了有轨电车在交叉口的停车,提高了有轨电车运行的稳定性。优化后社会车辆绿波带宽均大于20 s,表明有轨电车绿波系统并未对社会车辆产生过多干扰,实现了有轨电车和社会车辆的高效组织。

图5 绿波带宽图Fig.5 Green wave bandwidth graph
3.3 方案对比分析
为进一步对比体现文中模型方法的优化效果,进行了两个对比实验。
对比实验1:采用现状信号控制方案,将社会车辆速度范围设定为[30,35] km/h。
对比实验2:保持现状交叉口绿信比,将信号周期范围设置为[100,120] s,利用MULTIBAND 模型对社会车辆进行干线协调控制。优化得到最佳信号周期为113 s,信号控制方案如表6所示。

表6 对比实验2的信号控制方案Table 6 Signal control scheme of the comparative experiment 2 s
由于对比实验2将全线信号周期进行统一,因此优化后的信号控制方案在各路段均得到绿波带。由于该方案未考虑有轨电车的通行,其上下行绿波带宽占比与根据文中模型计算得到的优化方案相比有所增大,但由于信号周期与有轨电车发车间隔无倍数关系,有轨电车运行过程中存在交叉口停车等待通行的情况。
采用VISSIM 仿真软件对现行信号控制方案和优化后控制方案下社会车辆的运行状况进行仿真,评价数据通过行程时间检测器获得。路网仿真时间为1 h,预热时间为1 000 s。通过比较优化前后社会车辆的延误情况评价其运行状况,各方案的仿真结果如表7—9所示。为更直观地显示并对比各交叉口的延误,将表7—9数据整理成图6。


图6 交叉口延误对比Fig.6 Comparison of intersection delay
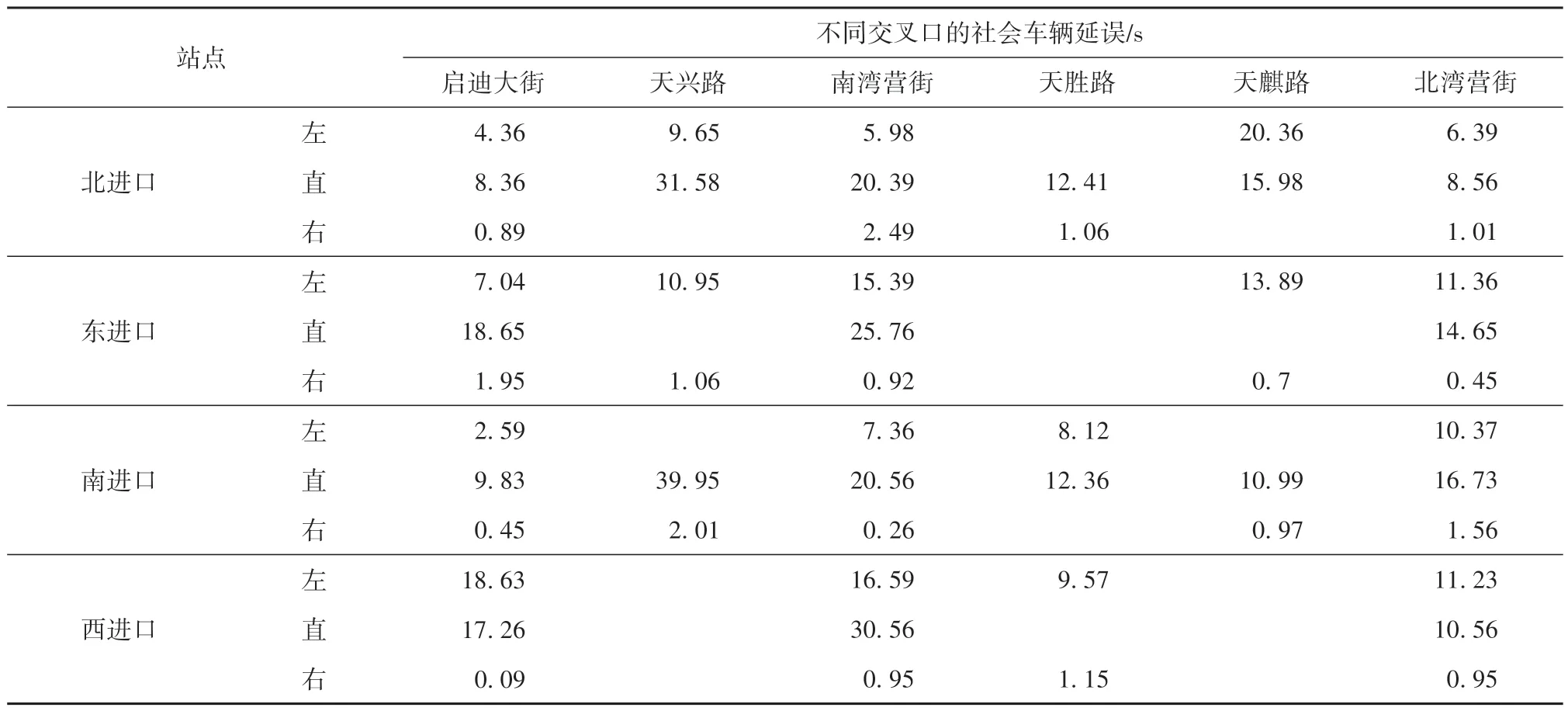
表7 优化模型的社会车辆延误Table 7 General traffic delay under the optimized model
仿真结果表明,与对比实验1相比,进行信号控制协同优化后,交叉口总延误分别降低35.24%、21.09%、28.26%、29.18%、20.89%和20.90%,其中对南北向直行车辆运行效率的改善效果较为明显。对比实验2将全线信号周期统一,对于运粮河东路—天兴路和运粮河东路—启迪大街两个流量较小的交叉口,其优化效果有限,延误增大。与文中提出的优化模型相比,对比实验2提升的社会车辆运行效率仅为6.04%。

表8 对比实验1的社会车辆延误Table 8 General traffic delay under the comparative experiment 1

表9 对比实验2的社会车辆延误Table 9 General traffic delay under the comparative experiment 2
对有轨电车在案例路段的运行进行仿真,结果表明:采用文中模型优化的信号控制方案时有轨电车行程时间稳定,上行方向行程时间为638.7 s,下行方向行程时间为605.3 s;对比实验1中上行有轨电车行程时间为598.5 s,下行有轨电车行程时间为617.8 s;对比实验2中上行有轨电车行程时间为723.3 s,下行有轨电车行程时间为653.9 s。
文中所提模型通过调整交叉口相位差与有轨电车行程时间,使有轨电车在交叉口无需停车,不产生额外的控制延误。对比实验1 与对比实验2 中有轨电车在交叉口的平均停车次数分别为0.50 次和0.67 次,上行平均控制延误分别为12.74 s/辆和28.91 s/辆,下行平均控制延误分别为14.29 s/辆和18.99 s/辆。与对比实验相比,模型减少了有轨电车在交叉口的停车与控制延误,且行程时间稳定,不存在因信号控制导致的行程时间变化,提高了有轨电车的服务水平。与模型优化结果相比,对比实验2未考虑有轨电车的通行需求,因而会产生较大延误;与对比实验1 相比,对比实验2 中交叉口信号周期更长,产生的延误较大。
综合社会车辆与有轨电车的延误,比较模型优化信号控制方案与对比实验2中信号控制方案下的人均延误,其中社会车辆平均载客量取为3 人/辆,有轨电车平均载客量取为150人/辆。结果表明:仿真时间段内,案例中人均延误为15.99 s/人,对比实验2 中人均延误为17.10 s/人。这说明文中提出的模型减少了6.94%的人均延误,提高了有轨电车在交叉口的运行效率,降低了交叉口的人均延误,提高了交通运行效率。
4 结语
1)文中提出的干线交叉口信号周期协调优化方法考虑了干线交叉口的交通需求,使干线分段绿波系统的信号周期与交叉口实际交通需求相适应,并与有轨电车发车间隔相协调。所提出的有轨电车站点位置协调优化方法利用站点与交叉口的位置关系对有轨电车绿波约束条件进行松弛,拓宽了模型的可行域,增大了社会车辆的绿波带宽。
2)文中提出的干线分段绿波协调控制优化模型以社会车辆双向可变绿波带宽最大为优化目标构建干线分段信号协调优化控制模型,同时协调周期不同的相邻交叉口间相位差,以保证有轨电车绿波的连续性,保障了有轨电车在交叉口的优先通行,并兼顾了社会车辆的通行效率。
3)文中方法同样适用于对发车间隔较大的BRT专用道系统的通行控制。此外,文中仅考虑了单线有轨电车的干线分段绿波协调控制方法,对于有轨电车复线共轨的情况,则需要对交叉口信号相序及相位差进行更为复杂的协调与优化,将干线绿波模型拓展至有轨电车网络层面,这将是下一阶段的研究重点。

