基于空间广义有序Probit 模型的高速公路事故严重程度分析
胡郁葱 韦湖 曾强
(华南理工大学 土木与交通学院,广东 广州 510640)
随着我国社会经济的高速发展,机动车保有量和公路通车里程持续增长,交通安全问题日益突出。作为道路交通运输网络的主骨架,高速公路具有行车速度快、货车等大型车比例高等特点,且为相对封闭的系统,一旦发生事故,容易导致严重的人员伤亡和巨大的财产损失。据统计[1],我国高速公路交通事故的致死率约为35%,远高于其他类型道路。如何降低高速公路事故的严重程度,是交通管理部门和安全研究人员面临的重要课题。为此,有必要深入探究高速公路事故严重程度的影响因素及其效应,为制定经济、有效的安全改善对策奠定基础。
近年来,国内外学者运用统计回归模型和机器学习方法对高速公路事故严重程度进行了大量研究[2-12]。例如,Yu等[2]采用二项随机参数Logit模型和支持向量机分析了实时交通参数(平均速度、速度标准差)和天气指标(温度、能见度、降水量)对美国科罗拉多州I-70 高速公路事故伤亡程度的影响。基于美国怀俄明州I-80 高速公路10 年间的交通事故数据,Haq等[3]采用贝叶斯层级二项Logit模型对各类型卡车事故(卡车单车事故、卡车与小汽车碰撞事故、卡车与SUV或皮卡车碰撞事故、卡车与卡车碰撞事故)的伤亡程度影响因素进行了计量分析研究,并通过贝叶斯二项Logit 模型分析了因爆胎导致的交通事故严重程度的影响因素[4]。这些研究均将事故严重程度划分为两个等级,例如无伤亡和伤亡事故、严重和非严重事故。当划分的严重等级超过两个时,则通常采用多项Logit/Probit、有序Logit/Probit及其改进模型对事故严重程度进行统计回归分析[5]。王磊等[6]分别采用多项Logit和有序Logit 模型分析了国内3 条高速公路上发生的227 起交通事故的严重程度。鉴于事故数据中未被观测的异质性,陈昭明等[7]采用混合Logit 模型(又称多项随机参数Logit 模型)分析了黑龙江省3 条高速公路的事故严重性,Hou等[8]则采用混合Logit模型对黑龙江省3条高速公路上发生的单车事故严重程度进行了回归分析。基于广东省开阳高速公路2014 年的交通事故严重性分析,Zeng等[9]构建了贝叶斯空间广义有序Logit模型,在表征事故严重等级间的有序关系的同时,避免了传统有序Logit模型对观测因素影响效应的限制,并解析了相邻路段上事故严重等级间的空间关联;Zhang等[10]则在多项Logit模型的基础上考虑事故间的空间关联,建立了贝叶斯空间多项Logit模型。在机器学习方面,Huang等[11]利用沪昆高速公路湖南段的交通事故数据,采用分类回归树识别了事故严重程度的重要影响因素及其交互作用;吕璞等[12]则采用深度卷积神经网络对广西境内的某山区高速公路严重程度进行了预测。
上述研究虽然分析了人、车、路、环境和路政救援等因素对高速公路事故严重程度的影响,但由于事故等级划分、分析方法和人文地理环境等方面的差异,研究结论并不完全统一。相对于两类严重等级划分,多类(不少于3类)严重等级划分通常能够更全面地反映真实的事故伤亡程度,同时也能更深入地揭示各类因素的影响。在分析方法上,统计回归模型相对机器学习方法的应用更为普遍。这主要是因为统计回归模型不仅能够对事故严重等级进行预测,而且能够清楚地解析其受到观测因素的影响效应及各类数据特征。异质性和空间关联是事故严重程度统计建模时考虑的两个重要问题[13],其中异质性体现了未被观测但与被观测因素相关的因素对事故严重程度的影响,空间关联则体现了未被观测的因素对空间相邻事故严重程度的共同影响。空间关联是异质性的重要来源之一。有研究表明[14],解析事故数据中的空间关联将显著降低甚至消除其异质性效应。尽管文献[9-10]中构建的贝叶斯空间模型展现了良好的拟合预测性能,但其考虑的是路段层面的空间关联,仅反映了未被观测的道路因素对相邻路段上发生事故的严重程度的共同影响。由于划分的路段长度不一,路段空间关联并不能完全准确地揭示事故间的空间关联程度,且未考虑单个事故的空间影响范围。
为此,文中采集了广深沿江高速公路东莞段2014—2019年的交通事故数据,将事故严重程度划分为3 类(无伤亡事故、轻伤事故和重伤亡事故),考虑事故间的空间相关性和单个事故的空间影响范围,建立基于不同距离阈值的贝叶斯空间广义有序Probit模型,分析涉事车辆、天气状况、道路条件、发生地点和时间、事故类型等因素对事故严重程度的影响。基于若干个空间关联距离阈值,构建事故空间关联矩阵,并根据模型的拟合性能确定事故间的空间影响范围。最后,根据模型参数估计结果识别事故严重程度的显著影响因素,计算显著因素的边际效应,量化其对不同严重等级事故发生概率的影响,以期为制定降低高速公路事故严重程度的改善方案及其经济性评价提供技术支持。
1 数据准备
广深沿江高速东莞段全长46.257 km,共设桥梁42.853 km,桥梁长度占路线总长的92.64%,设计速度为100 km/h,路段采用全封闭、全立交、控制出入的双向八车道高速公路标准。
课题组收集了广深沿江高速东莞段2014—2019年的事故数据,剔除含遗漏或异常数据的事故数据后,剩余的1 490 条事故数据用于研究。这些交通事故数据包含1 273 起无伤亡事故(占85%)、188 起轻伤事故(占13%)、14 起重伤事故(占1%)和15 起死亡事故(占1%)。由于重伤事故和死亡事故的比例过低,因此将这两类事故合并为重伤亡事故,据此将高速公路交通事故严重程度分为3 类:无伤亡事故、轻伤事故和重伤亡事故。这些事故按照其地点桩号排序后的严重程度分布如图1所示。

图1 事故严重程度的空间分布Fig.1 Spatial distribution of crash severity
为了衡量相邻事故间严重程度的相似程度,构造评价指标——平均严重程度绝对偏差MA,计算公式如下:
式中,yi为地点桩号从小到大排列的第i起事故的伤亡严重程度。经计算,这些事故的平均严重程度绝对偏差仅为0.29,接近于0,说明相邻事故间的严重程度相似度很高。
除了事故严重等级信息外,事故数据中还包含事故类型、涉事车辆信息、事故发生时间、天气情况、事故发生地点。参考以往相关研究[9-10],从道路、车辆、环境3个维度选取10个因素构建事故严重程度预测的解释变量集。表1给出了各变量的具体含义及描述性统计量。对于包含3 类或3 类以上的分类变量,若其中一类被选为参考项,则其他类别转化为0-1变量[15]。
2 模型建立与评价
鉴于事故严重程度间的有序关系以及相邻事故间的空间相关性,建立事故严重程度分析的空间广义有序Probit模型,并将其与传统多项Logit模型和广义有序Probit 模型进行对比。这些模型的基本结构、贝叶斯估计方法、评价指标和边际效应估计方法分别如下。
2.1 模型结构
2.1.1 多项Logit模型
多项Logit 模型基于效用理论拟合自变量与包含多个类别的分类变量间的内在关系。对于任一交通事故i,其严重程度的效用函数为
式中:Xi为事故i对应的影响因素观测值组成的向量;βk为这些因素对应事故严重程度k的回归系数组成的向量(包括常数项);严重程度k的取值1、2、3 分别表示无伤亡、轻伤和重伤亡事故;εi,k为随机项,并假定相互独立,且服从Gumbel分布(Ⅰ类广义极值分布)。
事故i严重程度为k的概率为
2.1.2 广义有序Probit模型
上述事故数据中划分的无伤亡、轻伤和重伤亡事故严重等级存在明显的有序关系,使得相邻事故严重等级间存在一定的相关性。广义有序Probit 模型是解析事故严重程度间有序关系的重要方法之一。对于任一交通事故i,构造潜变量zi,以表征事故的潜在伤亡倾向:
式中,β为影响因素集Xi对应的回归系数向量(包括常数项),随机项εi假定服从标准正态分布。
事故i的严重等级yi与其潜在伤亡倾向zi的映射关系为
式中,μi,0和μi,1为定义各事故等级边界的阈值,且满足如下关系:
Zi为μi,1的影响因素集,α为对应的回归系数向量(包括常数项)。不失一般性[16],令μi,0=0。
事故i严重程度为k(k= 1,2,3)的累积发生概率为
由此可以计算,事故i严重程度为k(k=1,2,3)的概率分别为
2.1.3 空间广义有序Probit模型
发生地点相邻的交通事故可能受到某些未被观测到的因素的共同影响,从而形成事故严重程度间的空间相关性。参考以往研究[9-10],在潜在伤亡倾向zi的链接函数中加入具有条件自回归先验的随机项ϕi以解释事故间的空间关联,从而构建空间广义有序Probit模型,即
式中:wi,j为事故i和事故j的空间邻接权重,令事故的空间关联距离阈值为ds,若事故j与事故i的距离di,j≤ds,则wi,j= 1,否则wi,j= 0;σϕ为空间关联项的方差参数。
对应地,事故i严重程度为k(k=1,2,3)的概率的计算公式分别如下:
2.2 贝叶斯参数估计
由于空间广义有序Probit 模型结构复杂,因此采用贝叶斯方法对上述模型进行参数估计。WinBUGS 是进行贝叶斯估计的主流软件之一,它根据参数的先验分布和整理的数据集,采用吉布斯抽样算法和马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)仿真,推断出参数的后验分布[17]。
由于缺少有效的先验信息,因此将均值为0、方差很大的正态分布N(0,104)作为模型中所有的回归系数(β和α中的元素)的先验分布,将γ分布γ(0.01,0.01)作为空间精度(方差的倒数)参数1/σϕ的先验分布。条件自回归正态分布由WinBUGS 中的Car.normal函数来表示。设定一条链进行150 000次MCMC 仿真迭代,并舍弃前100 000 次迭代,根据WinBUGS 中的Gelman-Rubin 统计量,判断MCMC仿真的收敛情况。
2.3 模型评价指标
采用偏差信息准则(Deviance Information Crite⁃rion,DIC,记为CDI)和各事故严重等级及全体数据的分类准确度(Classification Accuracy,CA,记为AC)比较各个模型的优劣。DIC综合考虑了模型拟合度和复杂度[18],其值越小代表模型的整体性能越好;当两个模型的DIC差值超过10时,可判定模型间具有显著的差异。DIC可以在WinBUGS软件中直接获取,其计算公式为
式中:为后验平均偏差,反映了模型的拟合程度;npD为有效参数的数量,体现了模型的复杂程度。
各事故严重等级的分类准确度衡量了模型对各严重等级的事故实现准确估计的比例,计算公式如下:
式中,为事故i的模型估计严重等级,yi为事故i的实际严重等级。
全体数据的分类准确度则衡量了模型对所有事故数据实现准确估计的比例,计算公式如下:
2.4 边际效应
虽然可以通过各因素对潜在严重倾向和阈值的系数估计量判别该因素是否对事故严重程度具有显著影响,但是并不能直接通过相应系数确定显著因素对各事故严重程度发生概率的影响。为此,需根据参数估计结果,进一步计算显著因素的边际效应。
以空间广义有序Probit 模型为例,连续变量x对严重等级k(k=1,2,3)的边际效应计算公式分别如下:
式中,βx和αx分别为变量x在潜变量zi和阈值μi,1拟合中的系数。
0-1 变量x对严重等级k(k=1,2,3)的边际效应计算公式如下:
3 结果分析
3.1 模型最优空间关联距离阈值的确定
为了探索事故间的空间影响范围,令其关联距离阈值分别为200、250 和300 m。根据前述贝叶斯方法获得的广义有序Probit 模型及各空间广义有序Probit 模型的评价指标结果及空间方差参数的估计量如表2所示。
由表2可知,基于各关联距离阈值的空间广义有序Probit模型的Dˉ值均明显小于多项Logit模型和广义有序Probit 模型,说明解释事故间的空间关联能够显著提高事故严重性分析模型的拟合性能[9-10]。尽管npD值表明空间广义有序Probit 模型更加复杂,但其更小的CDI值(与多项Logit模型和广义有序Pro⁃bit 模型的差值均超过了130)反映了空间模型更佳的综合性能。分类准确性结果进一步证实了空间广义有序Probit 模型的优越性。具体而言,除了在无伤亡事故等级上达到了100%的分类准确度外,空间广义有序Probit 模型在其他事故严重等级和全体事故上也都具有更高的分类准确度。尤其是针对重伤亡事故,多项Logit模型和广义有序Probit模型的分类准确度均为零,而空间广义有序Probit 模型最高达到了55.17%。重伤亡事故因造成了严重的人员伤亡,一直是社会大众和交通安全部门关注的重点,准确地估计和预测该类事故的发生概率对高速公路交通安全状况的改善具有重要的实践价值。此外,3 个空间模型中的空间方差参数估计量均明显大于0,充分说明了事故间高强度的空间关联性,进一步体现了空间广义有序Probit模型的合理性。
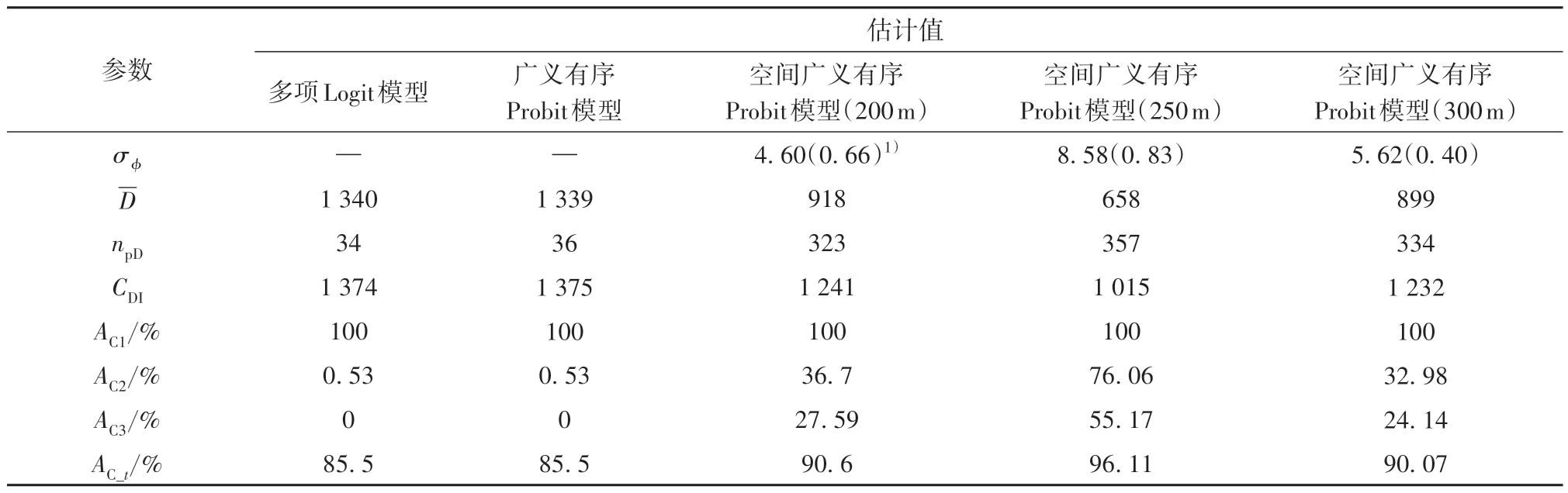
表2 模型结果对比Table 2 Comparison of model results
对比各空间广义有序Probit 模型可以发现:基于250 m 关联距离阈值的空间广义Probit 模型的CDI值最小(与其他空间模型的差值均超过了200),且分类准确度(尤其是对轻伤和重伤亡事故)最高,这些指标均体现了该模型的优异性能。而且,该模型中的空间方差参数估计量最大,说明以250 m 作为关联距离阈值能够最大程度地挖掘相邻事故间的空间相关性,用以解释未被观测到的因素对相邻事故严重程度的共同影响。综合以上结果,可以认为250 m是最佳的事故空间关联距离阈值。
3.2 事故严重程度影响因素分析
由3.1 节可知,基于250 m 关联距离阈值的空间广义有序Probit 模型综合性能最佳,因此根据该模型的参数估计结果识别对事故严重程度具有显著影响的因素(如表3所示),并以此估计其边际效应(如表4所示),量化显著因素对各事故严重程度发生概率的影响。
由表3 可知,单车事故、本省车、客车、货车、周末和曲率6个变量对潜在伤亡倾向具有显著影响,其他类型车辆和夏天这2个变量对轻伤与重伤亡间的阈值具有显著影响,而桥梁则对两者有显著影响。表3 中的9 个变量都是高速公路交通事故严重程度的显著影响因素。
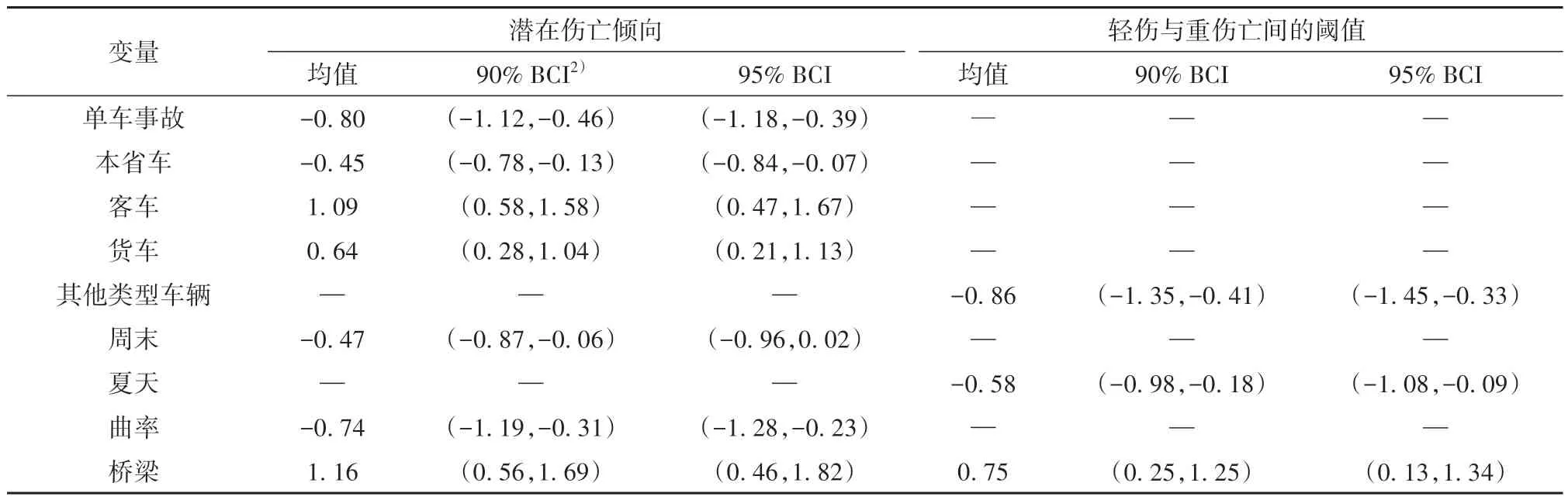
表3 基于250 m关联距离阈值的空间广义Probit模型的参数估计结果1)Table 3 Results of parameter estimation in the spatial generalized ordered Probit model with 250 m correlation distance threshold
由表4可知,单车事故比多车事故的严重程度低。具体而言,相对于多车事故,单车事故造成无伤亡的概率高7.58%,造成人员轻伤的概率低5.94%,造成人员重伤或死亡的概率低1.64%。这可能是因为多车事故涉及的人员和车辆更多,在事故发生时,驾驶员为了降低本车人员伤亡而采取的避险措施有可能对其他车辆的驾驶员和乘客造成更大的伤害;而单车事故涉及的人员和车辆较少,在事故发生时,驾驶员能够相对从容地采取有效措施来降低人员伤亡程度[9]。
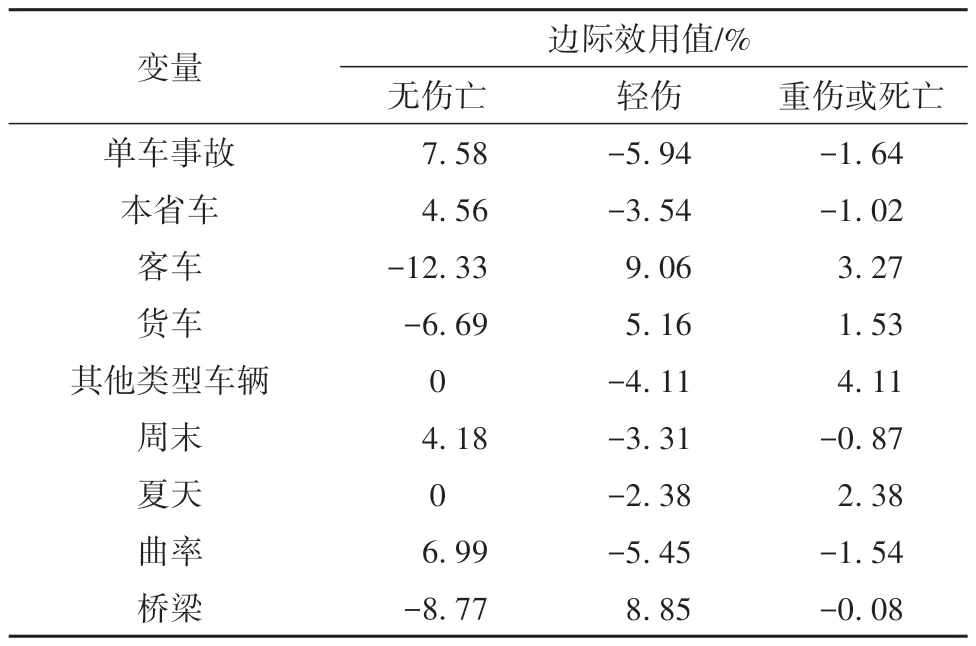
表4 显著影响因素的边际效用Table 4 Marginal effects of significant influential factors
相对于涉及外省车的交通事故,仅涉及本省车的交通事故导致无伤亡的概率高4.56%,导致人员轻伤的概率低3.54%,导致重伤或死亡的概率低1.02%。这可能是因为本省车驾驶员对道路交通环境更加熟悉,能够更快地感知道路上的行车危险源,并及时做出反应,从而降低了事故伤亡程度[19]。
在车辆类型方面,相对于小汽车间的交通事故,涉及客车、货车和其他类型车辆(例如,拖挂车、油罐车等)的交通事故都更容易导致人员伤亡,重伤亡的概率分别提高3.27%、1.53%和4.11%。根据文献[9,20]的研究结论,客车、货车和其他类型车辆相比于小汽车的体积和质量都更大,在事故发生时,会对其他车辆和人员造成更严重的伤害。
相对于工作日,周末发生的交通事故造成无伤亡的概率高4.18%,造成人员轻伤的概率低3.31%,造成人员重伤或死亡的概率低0.87%。Christoforou 等[21]也有类似的研究发现。对于本研究,这可能是因为周末往返广州、深圳及沿线的东莞等城市进行休闲娱乐、探亲访友的人员及车辆众多,车流量比工作日更大,车速相对较低,使得事故发生时的车辆间(或车辆与固定物体间)碰撞较轻,伤亡程度较低。
相比于春季,夏季发生的交通事故导致重伤或死亡的概率高2.38%。广深沿江高速公路位于北回归线以南并靠近南海,夏季频降暴雨且多伴随强风甚至台风,这些恶劣天气会显著恶化高速公路的安全行车环境。
道路平面曲率每增加1 km-1,无伤亡事故的概率增加6.99%,轻伤事故和重伤亡事故的概率分别降低5.45%和1.54%。道路曲率越大,曲线半径就越小,车辆通过该路段时的速度相对也就越低;而且,曲线段的设置将缓解因道路线形的单调性导致的驾驶疲劳,从而减少因驾驶员反应不及时导致的重大伤亡事故。
相比于非桥梁路段,桥梁上发生的交通事故导致人员轻伤的概率增加8.85%,重伤亡的概率降低0.08%。桥梁占广深沿江高速公路东莞段90%以上的路段长度,它能够有效减少高低起伏的地形地势条件对道路线形的不利影响,保持线路的整体平顺性,在保障高速公路交通运输效率的同时,提高其安全性水平,从而显著降低重伤亡事故发生的概率。
4 结语
基于事故间的空间关联,文中建立了贝叶斯空间广义有序Probit模型,分析了车辆类型与归属地、天气状况、发生时间和季节、道路曲率与坡度、事故类型等因素对高速公路事故严重程度的影响。DIC 和分类准确度等指标结果表明,空间广义有序Probit 模型优于多项Logit 模型和广义有序Probit 模型,且250 m 为最佳的空间关联距离阈值。研究发现:涉及客车、货车和其他类型车辆以及夏天发生的交通事故的严重程度相对较高;本省车、周末和曲率高的路段上发生的交通事故的严重程度相对较低,单车事故比多车事故的严重程度低。
本研究的不足之处在于:分析的高速公路范围较窄,采集的交通事故数据相对有限,且未能获取肇事驾驶人的相关属性;模型分析结果的可移植性仍有待检验。后续研究中,将对此进行改进,进一步提高模型的准确性。

