基于ELM 和MCSCKF 的锂离子电池SOC 估计

王 桥，叶 敏✉，魏 孟，廉高棨，武晨光

1) 长安大学公路养护装备国家工程研究中心，西安 710064 2) 新加坡国立大学机械工程系，新加坡 117576

在全球化石能源枯竭与环境污染加剧的国际背景下，电动车辆（Electrified vehicle,xEV）市场展示出了广阔的前景[1].动力电池作为新能源车辆的动力来源及储能元件，需要先进的电池管理系统（Battery management system,BMS）以确保其工作的安全性与高效性.荷电状态估计（State of charge,SOC）作为BMS 最重要的参数之一，是均衡管理、充电控制和里程预测等其他模块高效运作的前提.因此，精确的SOC 估计具有重要的意义[2-3].

当前，锂离子电池的SOC 估计方法主要分为四大类，包括：安时积分法（Ampere hour integral,AHI）、开路电压法（Open circuit voltage,OCV）、基于模型的方法（Model based method）和数据驱动法（Data based method）[4].安时积分法通过对电流进行积分来计算SOC，具有简单且易于应用的特点[5].但安时积分法的SOC 估计精度较低，其准确性严重受限于初始SOC 值和电流传感器的精度.OCV与电池SOC 具有较高的相关性，因此可以通过对OCV 与SOC 进行点对点的标定来实现锂离子电池SOC 的估计.但开路电压的获取通常需要很长时间，不能实现在线应用[6].同时，OCV 对温度较为敏感.因此，当环境温度发生变化时，OCV-SOC曲线会出现偏移.基于模型的方法所采用的模型主要包括：电化学模型、分数阶模型和等效电路模型.此方法通常与卡尔曼滤波联合实现SOC 的闭环估计[7].由于卡尔曼滤波只能应用于线性系统，一些非线性卡尔曼滤波被提出并应用于SOC 估计，包括：扩展卡尔曼滤波（Extended Kalman filter,EKF），无迹卡尔曼滤波（Unscented Kalman filter,UKF）和容积卡尔曼滤波（Cubature Kalman filter,CKF）[8-11].基于模型方法的SOC 估计精度主要依赖于精确的电池建模.但由于电池内部动态特性的复杂性和运行环境的多样性，精确的电池建模难以有效实现.同时，基于模型的方法的泛化性有限，当环境温度与行驶工况发生变化时，其精度会出现一定的波动.基于大数据的快速发展，数据驱动法受到了越来越多的关注.据统计，车辆每天可以产生大于4 TB 的数据量[12-14].同时，近年来出现了大量的车辆大数据平台.大数据平台与新能源车辆大数据的协同闭环发展，有利于数据驱动方法的快速发展.基于数据驱动的SOC 估计方法主要包括：高斯过程回归（Gaussian process regression,GPR）、循环神经网络（Recurrent neural network,RNN）和非循环神经网络.GPR 是一种常见的SOC 估计方法，GPR 可直接得到预测结果的不确定性，且通过最大边缘化的方式可以在节省算力的同时输出良好的正则化结果[15].但GPR 为非参数模型，单次的计算均涉及所有的数据点.因此，当数据量较大时，GPR 的计算效率低下[16].循环神经网络包括：长短时记忆（Long short term memory,LSTM）和循环门控单元（Gated recurrent unit,GRU）已经被广泛的应用于序列处理问题，且取得了不错的效果.LSTM和GRU 通过复杂的门控单元，实现了如同电路一般的复杂结构，可以实现长时间维度的数据记忆[17-18].但RNN 的训练通常需要较长时间.当迭代次数超过300 次时，基于CPU 的RNN 训练通常需要3000 s以上，且随着训练数据量的增大，其训练时间会指数式的上升.对比RNN，非循环神经网络的训练效率更高.其中，极限学习机（Extreme learning machine,ELM）随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需要设置隐含层神经元的个数，便可以获得最优解.因此，ELM 具有学习速度快、泛化性能好等优点[19].但基于简单的单层ELM 难以保证锂离子电池SOC 估计的高精确性[20-21].因此，本文提出一种基于极限学习机和最大相关熵平方根容积卡尔曼滤波（Maximum correntropy square-root cubature Kalman filter,MCSCKF）的SOC 估计方法.基于MCSCKF 方法，ELM 被设定为电池SOC 的测量方程，安时积分方程被设定为电池SOC 的状态方程.基于MCSCKF，大大减少了ELM 的SOC 估计误差，实现了精确的SOC 估计.同时为进一步减少ELM 的测量误差，本文提出利用灰狼优化（Grey wolf optimizer,GWO）对ELM 的训练参数进行优化[22].最后，所提方法在多工况和宽温度范围内被测试以验证其泛化性能.通过与LSTM 和GRU 进行多维度的对比，验证了所提方法的优越性.

1 极限学习机

极限学习机在2004 年由南洋理工大学提出，以改进反向传播算法（Back propagation,BP）、提升学习效率并简化学习参数[18].该算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，具有学习速度快、泛化性能好等优点.ELM 的结构如图1 所示，是一种单隐含层前馈神经网络，由输入层、隐含层和输出层组成，输入层与隐含层、隐含层与输出层神经元间全连接.温度数据与SOC 的相关性较低[23]，而电流电压作为直接可测得的电池外部信息，不仅易于获得，而且与SOC 的相关性较高.因此，本文直接将电流电压数据作为ELM 的输入，SOC 作为ELM 的输出.

图1 极限学习机拓扑结构Fig. 1 Topology of an extreme learning machine

假设有任意样本(xj,tj)，其中，xj=[xj1,xj2,···,xjn]T，tj=[tj1,tj2,···,tjm]T，则含有L个隐含节点的单隐含层神经网络可表示为:

其中，g(x)为激活函数，ωi=[ωi1,ωi2,···,ωin]T是第i个隐含层单元的输入权重，bi是第i个隐含层单元的偏置，βi=[βi1,βi2,···,βim]T是第i个隐含层单元的输出权重.

ELM 的目标是使得输入值的误差最小，可表示为:

即存在对应的 ωi、xj和bi，使得：

并可用矩阵表示为:

其中，H是隐含层节点的输出，β为输出权重，T为期望输出值.

2 最大相关熵平方根容积卡尔曼滤波

本文选用的卡尔曼滤波是容积卡尔曼滤波（CKF）的改进版本，即最大相关熵平方根容积卡尔曼滤波（MCSCKF）.为了提高SCKF 在处理非高斯噪声方面的性能，提出了MCSCKF，其详细流程见文献[11].最大相关熵准则用于替代传统的最小均方误差准则，以提高CKF 的鲁棒性.改进后的版本在处理高斯噪声时不仅保留了SCKF 的优势，而且在处理非高斯噪声时表现出很强的鲁棒性.MCSCKF 的主要流程如表1 所示.

表1 MCSCKF 主要流程Table 1 Main procedure of MCSCKF

图2 显示了本文的闭环SOC 估计示意图.基于闭环估计可以保证SOC 估计在实际条件下的鲁棒性.本文的SOC 闭环估计基于MCSCKF 滤波框架，利用GWO-ELM 对SOC 估计建模，并作为滤波的测量方程，安时积分法作为状态方程.其中，GWOELM 的输入为电流与电压，输出为SOC，安时积分方程的输入为电流，输出为SOC.

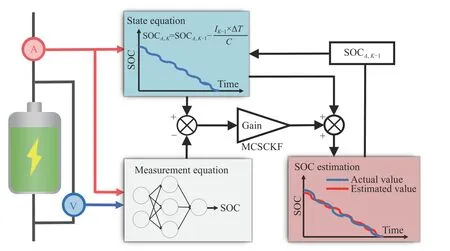
图2 基于MCSCKF 的SOC 闭环估计Fig. 2 Closed-loop SOC estimation realized by MCSCKF

参考文献[23]，温度数据与SOC 的相关性较低.因此本文仅将电压和电流作为ELM 的输入.MCSCKF滤波器的测量方程定义为：

其中，fELM表示ELM 的计算，t表示当前采样时间，U和I表示电压和电流，Rt表示测量噪声.

MCSCKF 滤波器的状态方程定义为：

其中，SOCA,t表示当前采样时间安时积分法的SOC值，ΔT表示当前采样间隔，C表示电池容量，Qk表示过程噪声.

3 实验与测试

电池测试平台由电池测试系统、东莞贝尔（DGBELL）恒温箱、上位机和被测电池组成，实验台如图3 所示.

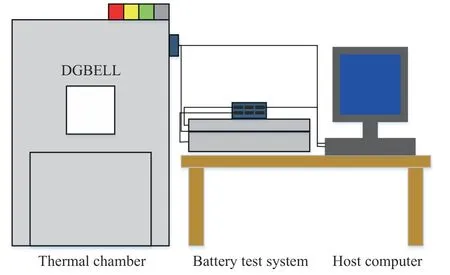
图3 实验测试平台Fig. 3 Experimental test platform

在本次实验中，相同规格的两个18650 电池被用来充放电测试，其详细参数如表2 所示.额定容量为2.2 A·h，额定电压为3.7 V，重43.8 g，内阻小于50 mΩ.

表2 被测电池详细参数Table 2 Detailed parameters of tested battery

共采用7 种行驶工况对被测电池进行测试，分别是：动态应力测试（Dynamic stress test,DST）、北京动态应力测试（Beijing dynamic stress test,BJDST）、高速公路驾驶循环（Highway driving schedule,US06）、联邦城市驾驶循环（Federal urban driving schedule,FUDS）、城市道路循环（Urban dynamometer driving schedule,UDDS）和2 种由前5 种循环随机组成的行驶工况.为模拟实验室温度和电池的正常工作温度，分别采用25 ℃和一个从10 ℃到40 ℃随机变换的温度来测试电池.被测电池使用0.5C 的恒流恒压（Constant current &constant voltage,CCCV）对其进行充电，直到电流小于0.05C 以确保电池充满.随后，对被测电池进行30 min 的静置，并开始之后的动态工况测试.部分实验数据如图4所示.

图4 部分循环下被测样本的电流电压曲线.(a) DST 工况；(b) US06 工况；(c) FUDS 工况；(d)随机混合工况-1Fig. 4 Current and voltage curves of the tested samples under partial cycles: (a) DST cycle;(b) US06 cycle;(c) FUDS cycle;(d) Mix-1

4 结果与讨论

本文的测试结果均基于一个配备Intel core-i7 9700 的中央处理器.为测试所提方法的泛化性能，1 号电池的实验数据为训练数据，2 号电池的实验数据为测试数据.同时，采用单一工况的实验数据为训练数据，混合工况的实验数据为测试数据.

4.1 混合工况测试

为测试所提方法的泛化性能，设计了一组随机工况随机温度的测试实验，分别命名为混合工况-1 和混合工况-2.在这两种测试工况下，被测样本从10 ℃开始放电，并在之后的20 和40 min 之后将环境温度分别增加至20 ℃和30 ℃，之后环境温度在20～40 ℃之间随机变化.测试循环由DST、BJDST、US06、FUDS、UDDS 随机组成.利用LSTM和GRU 所提方法进行对比，测试结果如图5 和表3所示.

图5 混合工况测试结果.(a)混合工况-1 测试结果；(b)混合工况-2 测试结果Fig. 5 SOC estimation results under a mixed drive cycle: (a) results under mix-1 cycle;(b) results under mix-2 cycle

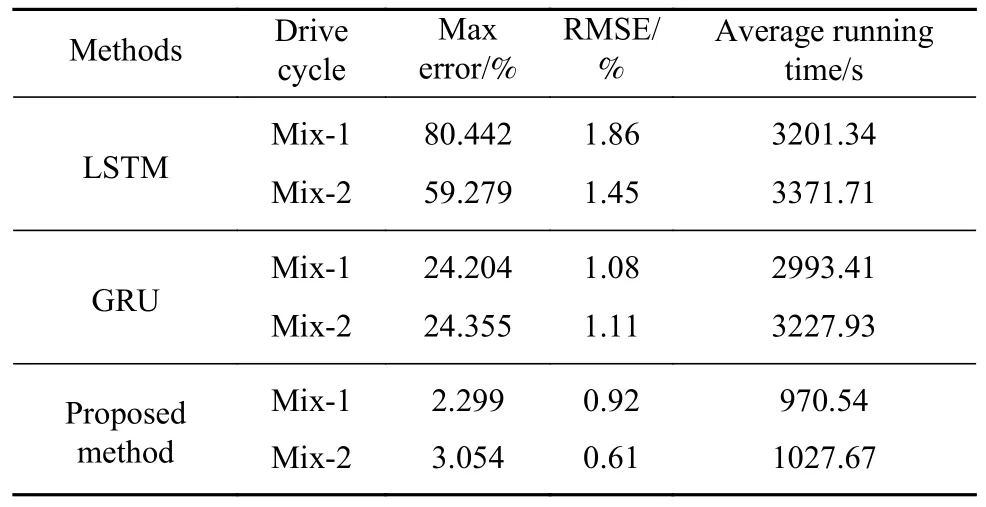
表3 混合工况测试结果Table 3 SOC estimation results under a mixed drive cycle

从测试结果可以看出，所提方法的运行时间和泛化性能均优于LSTM 与GRU.在Mix-1 工况下，所提方法的最大误差为2.299%，RMSE 为0.92%，平均运行时间为970.54 s；而LSTM 和GRU 的最大误差分别为80.442%和24.204%，RMSE 分别为1.86%和1.08%，平均运行时间分别为3201.34 s 和2993.41 s.在Mix-2 工况下，测试结果类似，所提方法的运行时间为LSTM 和GRU 的1/3，且测试最大误差与RMSE 优于LSTM 和GRU，验证了所提方法的优越性.相比较于单一的数据驱动方法，所提方法结合了物理模型法和数据驱动法的优势，在测试工况与测试温度随机变化时，表现出了更好的泛化性与鲁棒性.

4.2 鲁棒性测试

在应用MCSCKF 时，滤波的状态方程基于安时积分法，如式（6）所示，这意味着准确的初始SOC 值至关重要.然而，由于锂离子电池在不同条件下的容量变化，准确的初始SOC 值很难获得.另外，重启电池管理系统时，先前储存的SOC 值可能会丢失.因此，在初始SOC 值存在误差的情况下，算法的校正能力至关重要.本文共分4 种情况进行了所提方法的校正能力测试，分别为：初始SOC精确，初始SOC 为0.8，初始SOC 为0.6，初始SOC为0.4.测试结果如图6 所示.

图6 初始误差校正测试结果.(a)混合工况-1 测试结果；(b)混合工况-2 测试结果Fig. 6 Initial SOC error correction test results: (a) results under mix-1 cycle;(b) results under mix-2 cycle

从测试结果可以清楚的看出，所提算法在SOC初值错误的情况下可以快速收敛至准确值.当初始SOC 值为0.8 时，两种混合工况下的误差均在10 s 内收敛至10%以内，并在之后的20 s 内收敛至5%以内.当初始SOC 值为0.6 时，混合工况-1下的误差在38 s 时收敛至10%以内，混合工况-2下的误差则在22 s 时收敛至10%以内.当初始SOC值为0.4 时，混合工况-1 下的误差在64 s 时收敛至10%以内，混合工况-2 的误差则在36 s 时收敛至10%以内.混合工况-1 的收敛速度低于混合工况-2，且在初值误差增大的同时变得更加明显.经过数据分析发现，混合工况-1 的初始电流为负，意味着电池处于正常放电过程，而混合工况-2 的初始电流为正和零，这意味着少量的充电或搁置也许有利于初始SOC 误差的校正工作.因此，在所测试的不同初始SOC 情况下，所提方法均可以快速的收敛至准确值，这保证了所提方法的强鲁棒性.

为进一步测试所提方法在高噪声时的鲁棒性能[24-26]，参照国标GB/T38661—2020 规定的电池测量精度要求，电池单体电压测量误差绝对值不得大于10 mV，电流测量误差绝对值不得大于总量程的2%.因此，需要在测试数据集的电压信号中加入幅值为10 mV 的随机噪声，电流信号中加入120 mA 的随机噪声以测试SOC 估算的鲁棒性能.同时，利用应用广泛的LSTM 和GRU 与所提方法进行比较，测试结果如图7 所示.

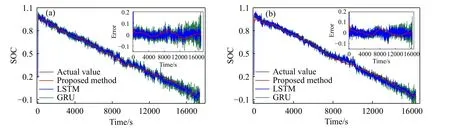
图7 随机噪声鲁棒性测试结果.(a)混合工况-1 测试结果；(b)混合工况-2 测试结果Fig. 7 SOC estimation in the case of random noises: (a) results under mix-1 cycle;(b) results under mix-2 cycle

从测试结果可以清楚的看出，所提方法在高噪声条件下仍可保证较高的估计精度，显示了其良好的鲁棒性能与实际应用价值.在两种混合工况下，所提方法的绝对误差在初始的波动后，均小于5%.相反，LSTM 和GRU 在初始的误差波动后，仍表现出很高的误差波动.在两种混合工况下，LSTM 的初始误差均超过80%，但之后的误差范围保持在10%以内，优于GRU 模型.相反，GRU的初始误差为20%，但之后的误差波动超过10%.综上，所提出的闭环估计方法，无论是在初值存在误差的情况下，或是在高环境噪声干扰的情况下，均保证了其良好的估计精度.因此，所提方法具有较好的鲁棒性能与应用价值.

5 结论

本文提出了一种基于ELM 和MCSCKF 的锂离子电池SOC 估计方法.并通过一系列实验予以验证.主要结论如下：

(1) 利用泛化性好、训练速度快的ELM 建立卡尔曼滤波的测量方程，并基于灰狼优化算法简化了ELM 繁琐的调参过程且提高了锂离子电池SOC的估计精度.

(2) 基于MCSCKF 实现了锂离子电池SOC 的闭环估计，可有效减少ELM 的SOC 估计误差，且在存在初始误差与干扰噪声的情况下，显示出了优越的鲁棒性.

(3) 利用LSTM、GRU 等序列处理能力强的神经网络与所提方法进行比较.结果表明，所提方法在运行时间与精度上都明显优于前两种方法.

(4) 进行了一系列的锂离子电池测试实验，所提方法的优越性在多工况循环、宽温度范围内取得了验证，显示出了良好的精确性、泛化性和鲁棒性.