一种块体-颗粒-杆件的耦合方法及其在隧道支护模拟中的应用

李晓光，李长洪，冯 春

1) 北京科技大学土木与资源工程学院，北京 100083 2) 中国科学院力学研究所，北京 100190

在高地应力环境下的节理岩体中掘进时，经常会发生断裂、破碎和坍塌现象.衬砌与锚杆联合支护是提高隧道稳定性的有效途径.在围岩稳定性（Rahaman 与Kumar[1]、Wu 等[2]）、岩爆（Wasilewski 等[3]、He 等[4]、Yang 等[5]）和隧道开挖和支护策略评估（Chen 等[6]、Liu 等[7]）等方面，已经开展了大量研究工作.

数值模拟是揭示复杂因素下隧道破坏机理的有效方法，也是评价隧道设计和施工方案合理性的有效手段.其中，有限元法（FEM）、有限差分法（FDM）和离散元法（DEM）是模拟此类问题的三种有用方法.

有限元法和有限差分法适用于模拟连续问题，如隧道的弹塑性变形，以及隧道在静、动荷载作用下的损伤和破坏过程.Sun 等[8]利用ABAQUS研究了隧道内支护结构（尤其是锚杆系统）在爆破荷载作用下的行为，得出了支护结构的损伤区域和损伤程度.Liu 等[9]基于扩展的Drucker-Prager模型和ABAQUS，提出了隧道开挖问题的半解析解和有限元数值模拟方法.Li 等[10]基于FLAC3D软件，提出了一套模拟拱锚联合支护效果的数值求解策略，该策略包括四个部分：可缩支护拱模块、可分离拱-岩相互作用模块、可破碎锚杆模块和高效围岩求解模块.Wang 与Qian[11]提出了考虑衰减约束效应的有限差分法，用于对应变软化岩体中开挖圆形隧道进行精确模拟.

离散元被广泛用于模拟隧道的渐进破坏和坍塌，其中颗粒离散元和块体离散元是两种典型的方法.Wu 等[12]利用三维离散元方法研究了隧道施工对相邻既有隧道的影响，并提出了一种保护既有隧道的新方法.Boon 等[13]提出了一种利用离散元方法进行中等节理岩体中隧道支护评估的系统方法，该方法的重点是利用锚杆与衬砌相互作用图来评价锚杆与衬砌厚度在隧道支护设计中的相对有效性.Wang 等与Cai[14]提出了一种DFN与DEM 耦合的多尺度建模方法，用于模拟节理岩体中的开挖响应，该方法兼具连续方法和非连续方法的优点.Chryssanthakis 等[15]采用UDEC 研究了纤维增强喷射混凝土和锚杆加固的相互作用机理及规律.

近年来，国内外的学者对连续介质方法与非连续介质方法的耦合开展了大量的研究.Huang等[16]通过将商用软件FLAC 与PFC 进行交互，实现了有限差分与离散元的耦合计算；该方法中，潜在的损伤区域用颗粒进行描述，完整的围岩用单元进行描述.Yang 等[17]和Saiang[18]也采用FDM和DEM 耦合模拟了隧道周围的大变形和损伤区.Lisjak 等[19]通过FEM 与DEM 的耦合研究了粘土页岩中圆形隧道的开挖稳定性，模拟结果突显了顺层剪切强度在控制开挖破坏带形成过程中的重要性.Liu 等[20]开发了基于GPU 加速的NMM，并对一系列隧道开挖模型进行了模拟，以验证该方法对深埋岩石隧道开挖损伤区模拟的能力.

有限元法能较好地描述松动区外围岩的弹塑性变形，离散元法能较好地描述松动区内围岩的损伤和破裂.目前，国内外专家学者虽然已经进行了大量与隧道开挖和支护相关的数值研究，但锚杆支护下有限元和离散元耦合的隧道稳定性数值算法研究较少.因此，本文提出了一种块体-颗粒-杆件耦合的数值算法，来模拟节理岩体中隧道开挖和支护的力学行为.

1 连续-非连续方法

本文的块体-颗粒-杆件耦合算法基于连续-非连续数值模拟方法（Continuum discontinuum element method，CDEM[21-22]）实现，故对CDEM 进行概述.

CDEM 是一种拉格朗日系统下的基于可断裂单元的动态显式求解算法.通过拉格朗日能量系统建立严格的控制方程，利用动态松弛法显式迭代求解，实现了连续-非连续的统一描述，通过块体（颗粒）间键的断裂来分析材料渐进破坏，可模拟材料从连续变形到断裂直至运动的全过程，结合了连续和离散计算的优势.

CDEM 是一种基于广义拉格朗日方程（式1）的网格-粒子高度融合的方法，该方法在能量层面上将有限元、块体离散元、颗粒离散元进行了统一，实现了三种数值方法的耦合计算.

式中，Qi为系统的非保守力；L为拉格朗日函数，ui、vi分别i方向的位移及速度，εij为应变.

对广义拉格朗日方程进行离散，最终可得到有限元的动力学方程为

颗粒离散元的动力学方程为

杆件单元的动力学方程可表述为

2 多种类型单元的耦合思路

2.1 总体思路

隧道开挖过程中，围岩应力将重新分布，并导致隧道周边局部应力集中，加之爆破开挖等手段导致隧道周边岩体强度的大幅下降，最终形成包围隧道断面近似环状的松弛破碎带（松动圈）.松动圈以内岩体较为破碎，为低应力区；松动圈以外岩体较为完整，为高应力区.若在隧道开挖过程中不及时支护，松动圈内的岩体强度将进一步降低，并最终导致松动圈内松散岩体的整体失稳、垮塌.为了模拟锚杆对松动圈及周边完整围岩的支护作用，本文提出了块体-颗粒-杆件耦合的方法.

该方法基于连续-非连续的数值模拟方法CDEM，采用离散颗粒簇表征隧道周边松动圈以内的破碎岩体，采用块体单元表征松动圈以外的完整岩体，采用杆件单元描述锚杆及锚索等杆系类支护结构，采用插值耦合的方式实现杆件单元与离散颗粒及块体单元间力与位移的传递，从而实现高应力环境下隧道开挖失稳过程的模拟及支护效果的评价.耦合示意图如图1 所示.

图1 块体-颗粒-杆件耦合示意图Fig. 1 Block-particle-bar coupling model

2.2 块体-颗粒耦合算法

块体与颗粒之间的耦合采用接触耦合的方式，通过构建法向及切向弹簧，实现接触力的传递，耦合示意图如图2 所示.图中，t1、t2、n分别表示接触局部坐标系的两个切向分量及一个法向分量.

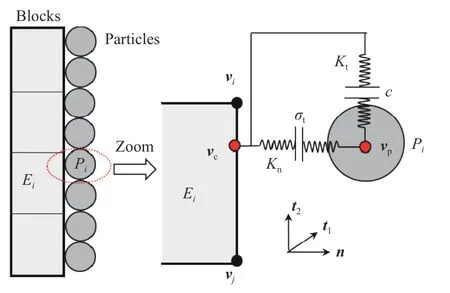
图2 块体-颗粒间的接触耦合示意Fig. 2 Block-particle coupling model

当块体单元Ei与颗粒Pi接触后，接触力的计算公式为

式中，F为局部坐标系下的接触力矢量，K为接触刚度矩阵，Δu为局部坐标系下的相对位移增量矢量，Δt表示计算时步，t表示当前时刻，t-Δt表示上一时刻.

接触力矢量F可表述为

式中，Fs1、Fs2及Fn分别表示切向接触力1、切向接触力2 及法向接触力.

接触刚度矩阵K的表达式为

局部坐标系下的相对位移增量矢量Δu的计算公式为

式中，T为局部坐标系转换矩阵，vp为整体坐标系下颗粒在接触点上的速度矢量，vc为整体坐标系下接触点上块体单元的速度矢量，vc的计算公式为

式中，vi为整体坐标系下与颗粒接触的块体某一个面第i个节点的速度矢量，wi为节点i对应的插值系数，N为块体接触面上的节点个数.

当考虑块体与颗粒接触面的断裂滑移时，需要引入拉伸断裂准则及剪切断裂准则.

拉伸断裂准则可表述为

式中，σt为抗拉强度，Aeq为等效截面积，本文令Aeq为颗粒的截面积.

当(13)式满足时，接触面发生拉伸断裂，本时步法向接触力将置零，同时抗拉强度σt及粘聚力c也将置零.

剪切断裂准则可表述为

式中，φ为内摩擦角，Fs为剪切方向合力，可表述为

当(14)式满足时，需要根据(16)式进行切向力的修正，同时将抗拉强度σt及粘聚力c置零.

2.3 块体-杆件耦合算法

有限元中经常采用公共节点的方式实现杆件与块体的耦合.此种方式要求杆件与块体单元的节点一一对应，并通过公共节点实现力的传递.此种方式对网格剖分器有一定的要求，复杂地层条件及存在大量杆件时难以剖分出适宜的网格.

为了在复杂地层中快速创建大量杆件，并实现杆件与块体单元的耦合计算，本文采用了插值耦合的方式.插值耦合时，杆件无需和单元共节点，因而大大简化了建模过程.插值耦合示意图如图3 所示.

图3 块体-杆件间的插值耦合示意Fig. 3 Block-bar coupling model

计算块体-杆件耦合时，需首先为每个杆件节点搜索与之匹配的插值单元.若杆件节点位于某单元的内部，则该单元即为插值块体.具体的计算公式可表述为

式中，X为杆件某一个节点的坐标向量，Ci为块体单元第i个面的面心坐标向量，Vi为第i个面的单位外法向量.

对块体单元的所有面进行式(17)的计算，若所有面获得的Ji均大于等于0，则表明该杆件节点位于该块体内部，该块体即为插值块体.

一旦杆件的某一节点找到了对应的插值块体，即可建立该节点与该单元的插值耦合关系，并采用沿着杆件轴向的罚弹簧Sgn以及垂直与杆件轴向的罚弹簧Sgs进行力与位移的耦合（图3）.Sgn主要用于描述杆件与围岩之间的拉拔效应及推压效应，Sgs主要用于描述杆件与围岩之间的侧向挤压效应（杆件侧向运动后与围岩间的拉伸作用较小，可忽略），具体的耦合公式为

式中，Fgn、Kgn以及Δugn分别表示杆件与围岩之间的推拉力、推拉刚度以及杆件轴向相对位移；Fgs、Kgs以及Δugs则分别表示杆件与围岩之间的侧向压力、侧压刚度及侧向相对位移.Δugn以及Δugs可表述为

式中，ubn和ubs分别表示某杆件节点沿着杆件轴向的位移及垂直与杆件轴向的位移，uen-i和ues-i分别表示与杆件节点对应的插值块体第i个节点沿着杆件轴向的位移分量及垂直与杆件轴向的位移分量.

为了表征杆件与围岩之间发生拉拔失效、推压失效的过程（图4），需要引入脆性破坏的Mohr-Coulomb 模型，如式(20)所示.

图4 杆件与围岩之间的拉拔（推压）失效示意.(a)轴向视图；(b)侧向视图Fig. 4 Pull and push failure between the bar and surrounding rock:(a) axial view;(b) lateral view

式中，cgb为杆件与围岩间的耦合粘聚力，μ为摩擦系数，σm为插值点的体应力，Ac为杆件与围岩之间的耦合面积，Ac可表示为

式中，Re为拉拔（推压）失稳面的等效半径（一般大于等于杆件半径），L为杆件节点所关联单元的长度平均值.

一旦式(20)中的fp≥0，杆件与围岩间发生拉拔或推压失效，此时将耦合粘聚力cgb至0，仅摩擦项发挥作用.

为了考虑杆件与围岩之间的侧向挤压失稳效应，需要引入理想弹塑性的挤压破坏模型，具体如图5 及式(22)所示.

图5 杆件与围岩之间的侧向挤压失效示意.(a)轴向视图；(b)侧向视图Fig. 5 Lateral compression failure between the bar and surrounding rock: (a) axial view;(b) lateral view

式中，σc为围岩的抗压强度.

一旦式(22)中的fc≥0，杆件与围岩发生挤压破坏，侧向挤压应力将等于围岩的抗压强度.

2.4 颗粒-杆件耦合算法

颗粒与杆件之间的耦合仍然采用罚函数法，首先判定杆件节点与颗粒的几何关系，一旦某杆件节点位于某颗粒的内部，即可建立该杆件节点与该颗粒的插值关系（图6）.

图6 颗粒-杆件间的插值耦合示意Fig. 6 Particle-bar coupling model

与块体-杆件之间的插值耦合方式类似，颗粒与杆件之间也设置沿着杆件轴向的罚弹簧Sgn以及垂直与杆件轴向的罚弹簧Sgs，采用脆性破坏的Mohr-Coulomb 模型进行拉拔破坏、推压破坏的判断，采用理想弹塑性的挤压破坏模型进行挤压破坏的判断.鉴于相关计算公式与块体-杆件的插值耦合公式基本一致，此处不再赘述.仅将杆件与围岩之间轴向相对位移及侧向相对位移的计算表述如下，为

式中，upn和ups分别表示颗粒在杆件轴向及垂直与轴向的位移分量.

3 计算案例

3.1 圆形盾构隧道弹性场验证

建立如图7 所示的二维圆形盾构隧道数值模型，隧道半径7.5 m，围岩整体半径75 m，模型外侧施加1 MPa 的径向压力.隧道围岩的密度为2500 kg·m-3，弹性模量为30 GPa，泊松比为0.25.距隧道中心30 m以内区域采用11852 个二维颗粒进行离散，以外区域采用34071 个三角形单元进行离散.

图7 圆形隧道数值模型Fig. 7 Numerical model of a circular shield tunnel

该模型中任意一点的径向应力σrr存在理论解[23]，为

式中，P0为模型外侧施加的压力，r0为隧道半径，r为模型中任意点到隧道中心的距离.

数值计算所得径向应力与理论解的对比如图8所示.由图可得，随着到隧道中心距离的增大，径向的压缩应力迅速增大，距离隧道2 倍洞径时，径向应力已达外侧压力的86%.数值计算所得的应力分布与理论解基本一致，证明了本文所述块体与颗粒耦合算法的正确性.

图8 数值解与理论解的对比Fig. 8 Comparison of numerical and analytical solutions

3.2 预应力锚杆加固矩形巷道

建立如图9 所示的矩形巷道模型，巷道尺寸3 m×4 m，巷道顶部距离地面7 m.数值模型采用14926个三角形单元进行离散，并对模型的底部及四周进行法向约束.巷道围岩的密度为2500 kg·m-3，弹性模量为30 GPa，泊松比为0.25.

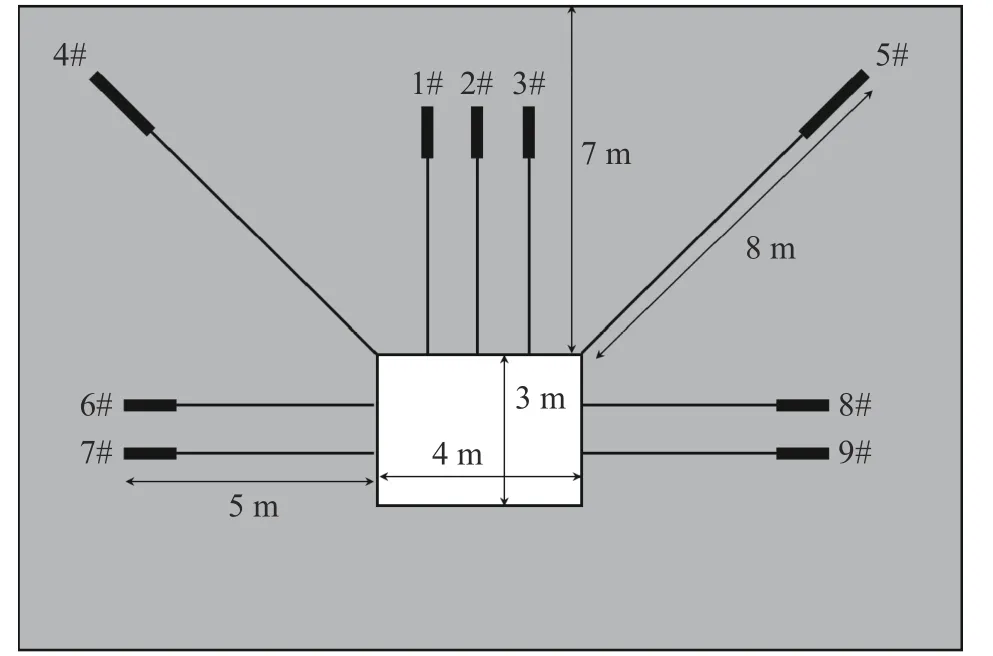
图9 矩形巷道预应力锚杆支护数值模型Fig. 9 Numerical model of a rectangular tunnel reinforced by prestressed rock bolts

采用9 根预应力锚杆对巷道截面进行加固，巷道侧壁及顶部的锚杆长度为5 m，巷道顶面与侧面交界处设置两根45°角的斜锚杆，长度为8 m.采用端锚形式，锚固段长度为锚杆全长的1/4.

对锚杆首端节点施加10 kN 的预拉力，同时向该节点所关联的实体单元施加与10 kN 等效的预压力.锚杆的自由段与实体单元的耦合粘聚力及摩擦系数均为0，锚固段的耦合粘聚力设为1 MPa，耦合摩擦系数为0.7.

本节仅为了观察预应力锚杆施加后对围岩受力状态的改变，故围岩采用线弹性模型，且不考虑围岩的自重.预应力锚杆施加后，巷道围岩的最小主应力（最大压应力）云图如图10 所示.由图可得，在预应力锚杆的加固作用下，围岩处于压紧状态；预应力施加点附近的局部区域，最大压应力值为17 kPa；在预应力锚杆自由段的控制区域内，围岩整体处于受压状态，压力值基本在8 kPa.

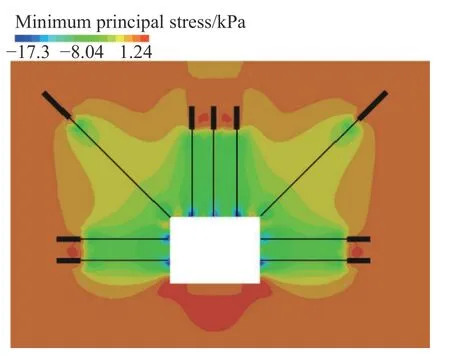
图10 最小主应力云图Fig. 10 Contour of the minimal principal stress

典型锚杆（2#、4#、8#）的轴力分布规律如图11所示.由图可得，自由段的轴力与设定值一致，为10 kN；进入锚固段后，锚杆上的轴力迅速减小为0.

图11 典型锚杆上的轴力分布Fig. 11 Axial force distribution of typical anchors

本节算例的计算结果表明，本文提出的杆件-块体耦合模型，可以较为准确地刻画预应力锚杆对围岩的加固作用.

3.3 全长连接锚杆对岩块的锚固作用

为了验证杆件与颗粒耦合算法的正确性，建立如图12 所示的全长连接锚杆加固岩块的二维计算模型.上下两个岩块的尺寸分别为0.5 m×1 m，在岩块中部设置长度为0.4 m，间距为0.2 m 的5 根竖直锚杆.整个计算模型采用11201 个颗粒进行离散，每根锚杆采用20 个杆单元进行离散.图12中，L表示锚杆间距，G表示重力加速度方向.

图12 锚杆加固岩块的计算模型Fig. 12 Numerical model of rock reinforced by full-anchored bolts

岩块的密度为2500 kg·m-3，弹性模量为30 GPa，泊松比为0.25，抗拉强度10 MPa，粘聚力20 MPa，内摩擦角35°.两个岩块间裂缝的强度设置为0.

全长连接锚杆的直径为2 cm，密度为7800 kg·m-3，弹性模量为210 GPa，泊松比为0.25，锚杆自身的抗拉及抗压强度为235 MPa，锚杆与围岩的单位长度耦合刚度为100 GPa，锚杆与围岩之间的耦合粘聚力为10 MPa，耦合摩擦系数为0.7.

模型的顶部进行法向约束，重力方向竖直向下.若没有全长连接锚杆的锚固作用，下部岩块将在自重作用下自然下落.设置如图12 所示的全场连接锚杆后，下部岩块被锚杆拉住，未发生掉落，岩块上的竖向应力云图如图13 所示.由图13 可得，锚固区域内出现了一定的挤压应力，锚固区顶部出现了较大的拉应力，表明全长连接锚杆发挥了作用.

图13 锚杆加固后岩块上的竖向应力云图Fig. 13 Vertical stress contour of the rock reinforced by full-anchored bolts

设从左至右5 根锚杆的编号分别为1#～5#，则该5 根锚杆的轴力变化规律如图14 所示.由图可得，锚杆上的轴力基本呈三角形分布，在裂缝处轴力最大，在两侧的轴力最小.裂缝处锚杆所受轴向拉力约2.45 kN，5 根锚杆合计12.25 kN，与下部岩块的重力基本一致.

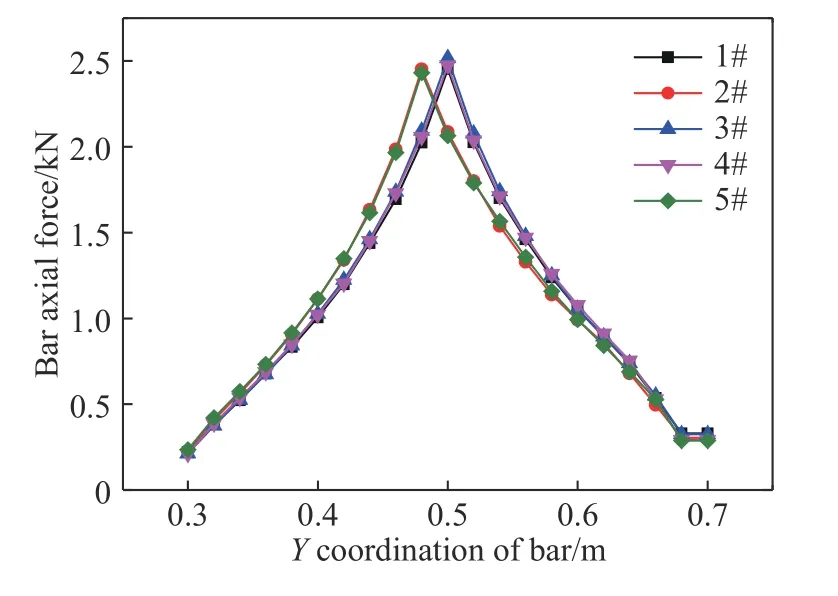
图14 锚杆上的轴力变化规律Fig. 14 Distribution law of the axial force on the bolts

3.4 碎裂岩体中的隧道开挖支护效果分析

建立如图15 所示的计算模型.模型外部尺寸为40 m×35 m，模型中心设置一直墙圆拱隧道，隧道底部距模型底部11 m，隧道顶拱为半圆，直径为10 m，直墙高度为4 m，隧道衬砌厚度为20 cm.隧道周边为不规则的松动圈，平均厚度为3 m.断面上设置29 根直径2 cm 长5 m 的全长连接锚杆，锚杆间距为1.0 m.隧道周边较完整岩体及隧道衬砌采用14436 个有限元单元进行描述，松动圈采用10011 个颗粒进行描述，每根锚杆采用25 个杆单元进行描述.借助前述的罚函数耦合方法，通过建立颗粒与杆件、块体与杆件、块体与颗粒之间的接触弹簧，即可实现锚杆-松动圈-完整围岩的耦合计算.

图15 隧道开挖支护模型Fig. 15 Tunnel excavation support model

隧道围岩、松动圈及衬砌结构的力学参数如表1 所示.

表1 力学参数Table 1 Mechanical parameters

锚杆的物理力学参数为，密度7800 kg·m-3，弹性模量210 GPa，泊松比0.25，锚杆自身的抗拉及抗压强度为235 MPa，锚杆与围岩的单位长度耦合刚度为100 GPa，锚杆与围岩之间的耦合粘聚力为10 MPa，耦合摩擦系数为0.7.

计算时，模型底部及四周法向约束，在模型顶部施加10 MPa 地应力，模拟400 m 埋深.本案例中自重应力是第一主应力，水平应力由弹性应力场计算获得，为第三主应力.

共模拟了无支护（A 工况）、仅衬砌支护（B 工况）以及衬砌锚杆联合支护（C 工况）3 种工况.三种工况下隧道的变形破坏情况如图16 所示.由图可得，A 工况下，整个隧道松动圈发生了失稳垮塌，隧道顶部及侧壁岩体均垮落至隧道内.B 工况下，虽然隧道整体处于稳定状态，但隧道底板的两端已经出现了明显的破裂，且底板出现了不均匀的台升（最大台升高度已达16 cm），隧道两侧直墙水平位移过大（约为17 cm），隧道顶部松动圈与外侧围岩出现明显分离现象.C 工况下，隧道整体处于稳定状态，底板、顶部及侧墙的位移均较小，表明锚杆发挥了作用，将隧道衬砌与周围完整围岩连接在了一起，对中间的松散夹心层形成了挤压加固的作用，阻止了松散层的进一步变形破坏.

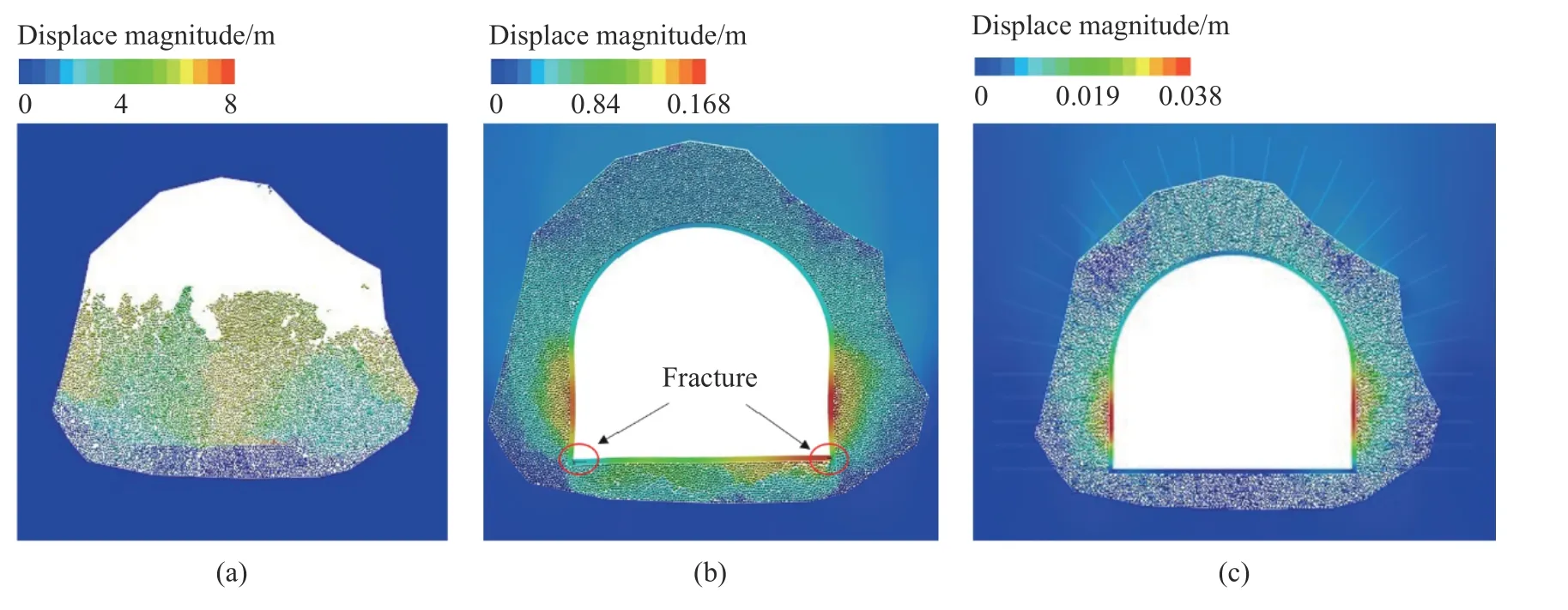
图16 三种模拟工况下隧道的总位移云图.(a)工况A;(b)工况B;(c)工况CFig. 16 Displacement magnitude contour of the tunnel under three numerical cases: (a) case A;(b) case B;(c) case C

C 工况下，各锚杆所受到的轴力情况如图17所示，图中锚杆位置红色区域表示拉伸状态，黑色区域表示压缩状态，横向宽度越大表示所受轴力的绝对值越大，轴力变化范围为-73.8～73.8 kN.由图可得，锚杆所受轴力沿着隧道轴线基本呈对称分布，侧墙处的水平锚杆所受到的轴力较大，顶部锚杆所受到的轴力较小，且越靠近顶部中心区域轴力越小.锚杆在松动圈内的部分，均呈现出了较大的轴向拉应力，这主要是因为松动圈内围岩较为松散，有向隧道内运动的趋势，锚杆对这些具有运动趋势的颗粒进行了限制，通过拉伸、牵引、拖拽等作用，对松散颗粒进行加固.对于完整岩体中的锚杆部分，所受轴力较小，但基本仍以拉伸为主.各锚杆基本处于拉伸状态，仅在松动圈与围岩交界面附近局部区域处于压缩状态.

图17 锚杆中的轴力分布Fig. 17 Axial force distribution in bolts

已知锚杆的直径为2 cm，抗拉强度为235 MPa，单根锚杆所能承受的极限载荷为73 kN.由图17可得，锚杆在拉伸及压缩状态下均有部分杆件单元达到了73 MPa，故绘制锚杆单元破坏状态图如图18 所示，图中红色实心圆点表示此处锚杆单元已经发生破坏.由图可得，隧道左右侧墙松动圈内的锚杆节点基本都达到了拉伸破坏状态，表明锚杆在抵抗松动圈内的变形破坏方面发挥了作用；隧道顶部区域锚杆受力较小，并未出现拉伸破坏.

图18 锚杆的破坏状态Fig. 18 Failure state of bolts

典型锚杆（锚杆位置如图15 所示）上轴力的变化规律如图19 所示.由图可得，1#、3#锚杆的轴力变化规律基本一致，整根锚杆均处于受拉状态，松动圈（3 m）内的锚杆拉力为73 kN 左右，局部位置拉力较小；松动圈之外，锚杆轴力逐渐减小至20 kN；2#锚杆在隧道衬砌附近处于受拉状态，拉力约为70 kN；衬砌之外，锚杆上的受力几乎为0.

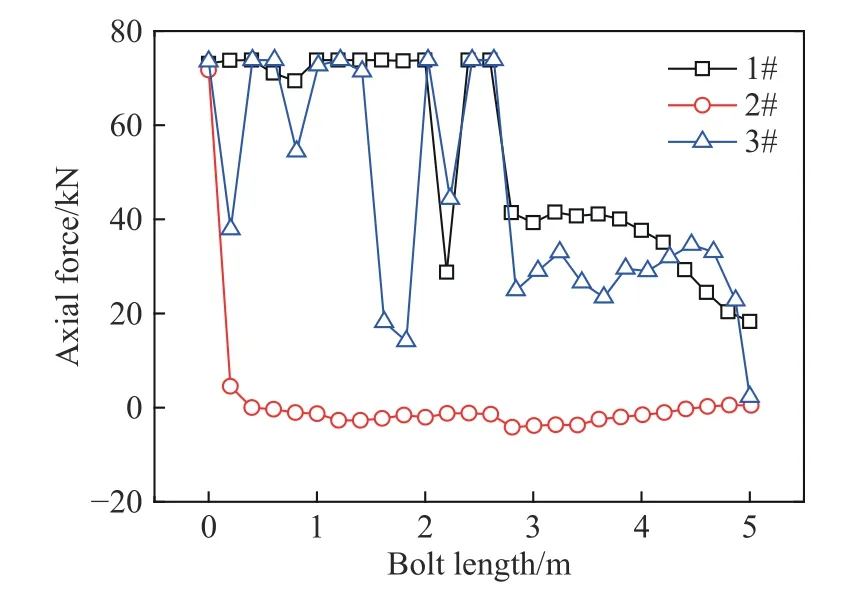
图19 典型锚杆轴力的变化规律Fig. 19 Relationship between axial force and bolt length

1#、2#、3#三根锚杆的轴向位移变化规律如图20 所示.由图可得，1#、3#锚杆的轴向位移变化规律基本一致，整根锚杆处于拉伸状态，隧道侧锚杆节点的轴向位移最大，约为20～30 mm；随着到隧道距离的增大，轴向位移逐渐减小，距离隧道3 m以外（松动圈以外），轴向位移基本保持不变.2#锚杆绝大部分区域的轴向位移为负值，但位移绝对值较小，表明该锚杆处于小幅压缩状态.

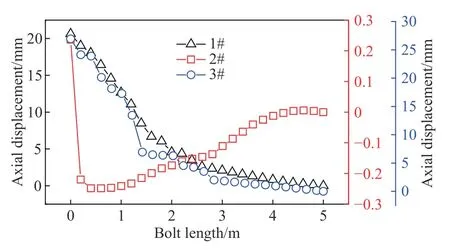
图20 典型锚杆轴向位移的变化规律Fig. 20 Relationship between axial displacement and bolt length

由前述分析可知，隧道开挖后，隧道周边岩体的应力将会重新调整，左右侧墙的竖向应力将会逐渐增大，顶部的竖向应力将会逐渐减小，衬砌锚杆联合支护对该隧道松动圈的控制效果明显，隧道变形控制在了4 cm 范围内，且衬砌未出现明显破坏.隧道顶部的加固作用主要由拱形衬砌来承担，顶部围岩通过松动圈传递的竖向应力，借由拱形衬砌传递至隧道侧墙；在拱顶区域，围岩基本处于受压状态，故锚杆的支护作用不明显.隧道侧墙的加固作用主要由锚杆来承担，隧道顶部的压应力载荷向侧墙传递并导致侧墙向隧道内变形，形成了具有一定空间范围的张拉变形区，锚杆对这一区域具有明显的“牵拉拽”作用，锚杆的部分区域已经发挥到了极限状态，松动圈的变形破坏效应得到了有效抑制.

4 结论

提出了一种有限元块体、离散元颗粒与有限元杆件的耦合方法，该方法通过罚弹簧的形式，实现了块体、颗粒及杆件之间力与位移的传递.其中，块体与颗粒之间采用接触耦合方式，采用1 根法向弹簧及2 根切向弹簧进行表征，在法向弹簧上可考虑拉伸破坏效应，在切向弹簧上可以考虑剪切断裂效应.杆件与块体及杆件与颗粒之间的耦合模式基本一致，均采用插值耦合的形式，采用1 根沿着杆件轴向的弹簧及1 根垂直于杆件轴向的弹簧进行表征，可分别考虑杆件的拉拔效应及侧向挤压效应.

将本文所述方法在隧道开挖支护中进行应用，4 个案例的计算结果表明了本文所述方法的计算精度及合理性.借助本文所述方法，可对高地应力下隧道开挖的破裂失稳过程及锚杆（锚索）对隧道的支护过程进行精确模拟.