基于乌鸦搜索算法的行星滚柱丝杠参数优化
蔡 威,刘 更✉,马尚君✉,周 勇,付晓军,张建新
1) 西北工业大学机电学院陕西省机电传动与控制工程实验室,西安 710072 2) 西北工业大学航空学院,西安 710072 3) 湖北江山重工有限责任公司,襄阳 441057
行星滚柱丝杠(Planetary roller screw mechanism,PRSM)是一种能够实现将旋转运动转化成直线运动的新型传动机构[1-3],具有大推力、高精度、长寿命等特点[4-6],逐渐应用于航空航天[7]、武器装备[8]、精密机床[9]、医疗器械[10]等领域.不同的领域对PRSM 有着不同的设计要求,通过合理设计PRSM结构参数,实现PRSM 螺纹副无侧隙啮合,提高传动精度.并且合理调整PRSM 参数,使其体积降低,进一步使其质量得到优化,有利于减少功率消耗,提升传动效率.因此,为优化PRSM 性能、减少设计成本,需要对PRSM 参数进行优化设计研究.
目前,国内外学者针对PRSM 啮合原理、运动学、动力学等方面进行了研究,赵英等[11]采用啮合区域中设置多个层面的方法,计算丝杠和滚柱以及螺母之间啮合位置与轴向侧隙.程远与范元勋[12]建立PRSM 螺旋曲面空间啮合坐标方程,精确计算出零侧隙时PRSM 几何参数,并且考虑了螺距误差、牙型半角误差、中径误差以及滚柱型面圆弧半径误差对PRSM 啮合状态的影响.付晓军等[13]建立丝杠、螺母和滚柱螺旋曲面方程,利用接触曲面连续相切原理,提出PRSM 螺纹副啮合点位置以及轴向间隙的方法.Ryakhovskiy 等[14]通过对螺纹曲面进行网格划分,利用网格曲面坐标差值计算出啮合点的位置.Sandu 等[15]推导了考虑螺纹截面轮廓为不同曲线时螺旋曲面方程,并计算得到螺纹啮合点的位置.Velinsky 等[16]建立PRSM 运动学模型,研究发现滚柱与丝杠之间存在滑动现象,滚柱与螺母之间只有当其内齿圈分度圆直径之比和其两零件螺纹中径之比不等时,产生相对滑动.党金良等[17]分析了反向式PRSM 机构工作原理和传动几何关系,建立PRSM 运动学模型,利用多体动力学仿真软件ADAMS 进行了验证.上述文献研究表明PRSM 螺纹牙结构参数、滚柱端部轮齿结构参数等对啮合位置、运动学以及动力学等均有较大影响.因此,PRSM 结构参数选择以及优化设计对整个机构传动性能极其重要.为提升PRSM 传动精度,确保机构结构强度,需要进一步开展PRSM 结构参数优化研究.
针对PRSM 结构参数优化方面有了一定研究.邢思等[18]以丝杠为研究对象,主要考虑丝杠的耐磨性、稳定性、强度以及螺纹剪切强度,设计出最佳丝杠参数.韦振兴等[19]将PRSM 部分结构参数作为设计变量,利用模拟退火法对其进行结构优化.高扬等[20]将内齿圈和滚柱端齿的变位系数作为设计变量,确定优化设计目标函数,通过对几何结构分析,建立变位系数优化数学模型,采用复合形法求解方法获得最佳变位系数.王佳丽[21]通过遗传算法设计滚柱端部变位齿轮副,以提高重合度减小体积为目标建立适度函数,得到了PRSM优化参数.但上述研究并没有同时综合考虑PRSM螺纹副和齿轮副结构参数优化问题,因此,需要对其进行开展研究,以获取最佳结构参数.
本文以PRSM 结构参数为优化设计变量,考虑PRSM 螺纹副啮合位置的影响,分析各零部件之间的受力,以各零件强度、无干涉啮合等为约束条件,螺母外径、丝杠中径、滚柱长度等结构参数最小为优化目标,建立PRSM 结构优化模型.
1 行星滚柱丝杠结构参数设计
PRSM 主要由滚柱、丝杠、螺母、内齿圈、保持架以及弹性挡圈等组成,如图1 所示.在工作过程中,丝杠做旋转运动,螺母在外负载的作用下只能做直线运动,驱使滚柱围绕丝杠做公转运动的同时还做自转运动,并且带动保持架绕着丝杠做公转运动.滚柱端部轮齿结构与内齿圈啮合,确保了丝杠、螺母与滚柱间啮合传动同步性.
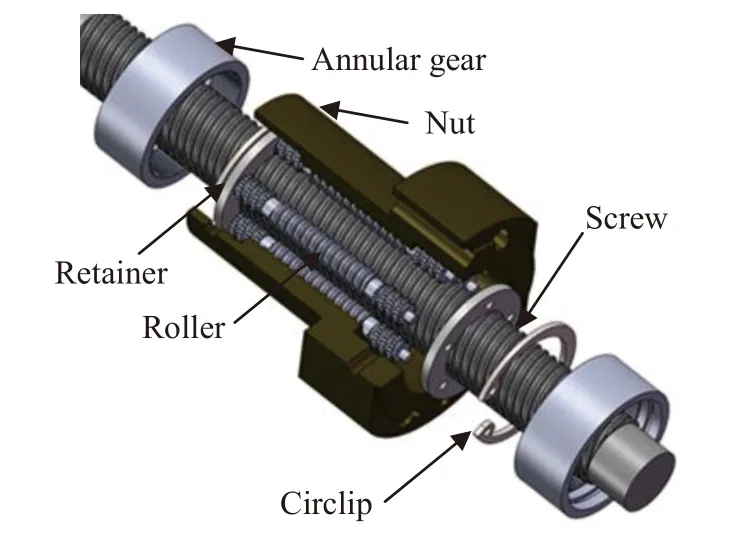
图1 PRSM 结构图Fig. 1 Structure graphing of PRSM
1.1 PRSM 基本参数确定
由PRSM 工作原理和几何条件可知,滚柱、丝杠和螺母螺纹旋向相同,螺距相等,即:
式中,Ps、Pr和Pn表示丝杠、滚柱和螺母螺距.
为保证PRSM 传动比是常数,并且保证滚柱与螺母不会产生相对轴向位移,通常使丝杠与螺母螺纹头数相等,滚柱一般为单头螺纹,即:
式中,ns、nn表示丝杠、螺母螺纹头数.
当丝杠旋转一周时,滚柱相对丝杠产生轴向位移为一个导程,滚柱由于自转和公转运动相对于丝杠产生的轴向位移和为0.因此,丝杠头数为:
式中,ds、dr表示丝杠、滚柱螺纹中径.
由式(2)和(3)可得螺母螺纹中径为:
式中,dn表示螺母螺纹中径.
丝杠螺旋升角为:
式中,λs表示丝杠螺旋升角.
同理,可得滚柱螺旋升角为:
式中,λr表示滚柱螺旋升角.
螺母螺旋升角为:
式中,λn表示螺母螺旋升角.
结合式(4)、(6)和(7),可以得到:
1.2 螺纹副啮合侧隙与螺纹牙厚关系
PRSM 中滚柱、丝杠以及螺母啮合曲面均是由截面绕着螺旋曲线旋转形成的空间螺旋曲面.如图2 所示,O-xiyizi表示系统全局坐标系,O'-uiviwi表示截面坐标系,Ω1、Ω-1分别表示上、螺旋曲面,Q表示螺旋曲面任意一点,θ表示该点所在截面与初始截面的夹角,r表示该点到zi轴的距离.因此,螺旋曲面任意一点Q相对于全局坐标系位置坐标为:
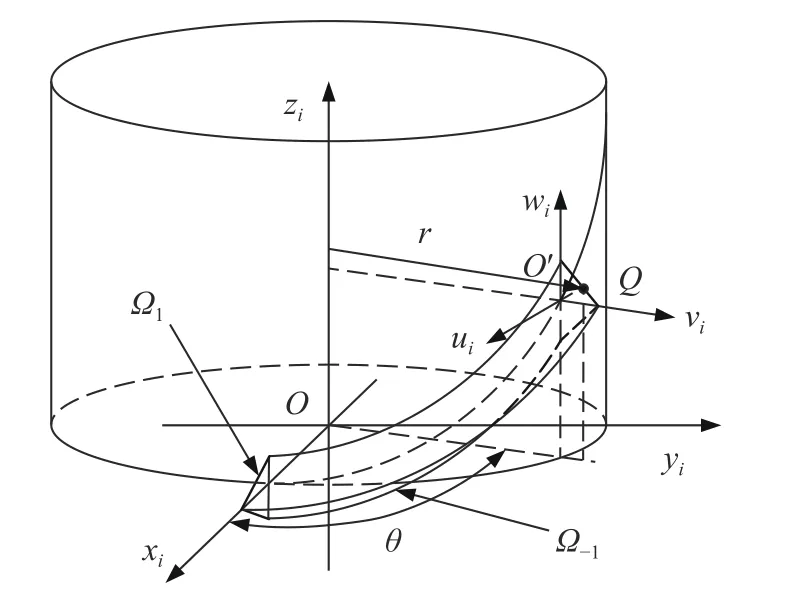
图2 空间螺旋曲面Fig. 2 Space helix surface
式中,f(r,θ)表示与r和θ有关的一个函数.
为了减少PRSM 摩擦、提高传动效率,通常将丝杠、螺母螺纹牙截面轮廓加工成斜线,将滚柱螺纹牙截面加工成圆弧形.如图3 所示,ai、bi、ci、βi、ri分别表示丝杠、滚柱和螺母螺纹牙全齿高、齿底高、牙厚、牙型角以及螺纹半径,i=s、r 和n 分别对应丝杠、滚柱以及螺母,rtr表示滚柱螺纹牙曲面半径.
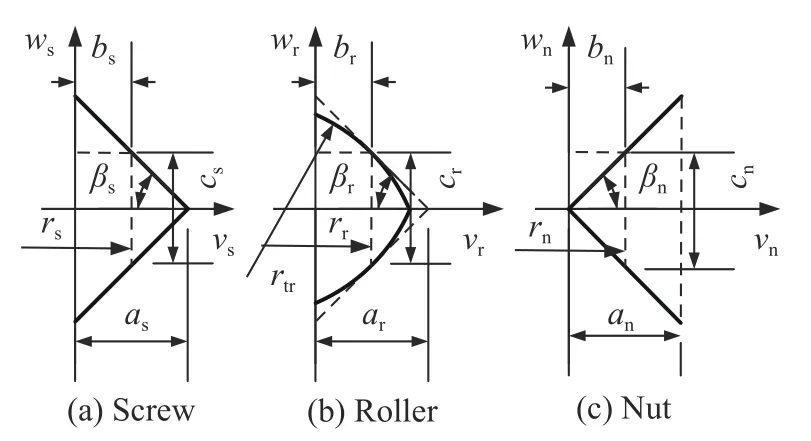
图3 丝杠(a)、滚柱(b)以及螺母(c)螺纹牙轮廓Fig. 3 Thread profile of the screw (a),roller (b),and nut (c)
因此,丝杠牙廓曲线在局部坐标系O'-usvsws坐标方程为:
式中,ζs值为1 或者-1,当为1 时,表示丝杠上牙廓曲线,为-1 时,表示丝杠下牙廓曲线.
滚柱牙廓曲线在局部坐标系O'-urvrwr坐标方程为:
式中,ζr值为1 或者-1,分别表示滚柱上牙廓曲线、下牙廓曲线.
螺母牙廓曲线在局部坐标系O'-unvnwn坐标方程为:
式中,ζn值为1 或者-1,分别表示螺母上牙廓曲线、下牙廓曲线.
由于PRSM 空间螺旋曲面是利用截面曲线绕着螺旋曲线旋转形成凹凸面,根据截面曲线方程,可以得到丝杠、滚柱以及螺母空间螺旋曲面方程分别为:
式中,ls、lr和ln表示丝杠、滚柱和螺母螺距.
式(14)分别对rs和θs求偏导数,可得该方向上的切向量(cosθs,sinθs,-ζstanβs)、(-rssinθs,rscosθs,ls/2π),因此,丝杠上空间螺旋曲面上任意一点的法向量为:
同理可得滚柱空间螺旋曲面任意一点处的法向量为:
螺母空间螺旋曲面任意一点处的法向量为:
如图4 所示,丝杠与滚柱啮合点位置.其中Qsr表示丝杠与滚柱实际啮合点,rrs表示滚柱侧啮合点处的半径,rsr表示丝杠侧啮合点处的半径,θsr表示丝杠侧的啮合偏角,θrs表示滚柱侧的啮合偏角,rr表示滚柱中径,rs表示丝杠中径.
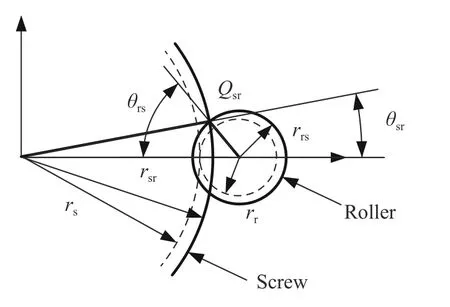
图4 丝杠与滚柱啮合点位置Fig. 4 Meshing position of the screw and roller
以丝杠上螺旋曲面和滚柱下螺旋曲面啮合为例,ζs值为1,ζr值为-1.根据空间曲面接触条件可知,丝杠与滚柱在啮合点处的单位法向向量相等.因此,丝杠与滚柱啮合方程为:
式中,βsr表示滚柱与丝杠啮合处的牙侧角,即:
同理,可以得到螺母与滚柱啮合关系图,如图5所示.Qnr表示螺母与滚柱实际啮合点,rnr表示螺母侧啮合点处半径,rrn表示滚柱侧啮合点处半径,θrn表示滚柱侧的啮合偏角,θnr表示螺母侧的啮合偏角.此时,ζn值为-1,ζr值为1.因此,螺母与滚柱啮合方程为:
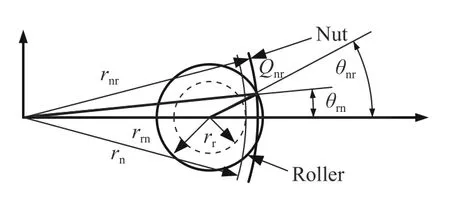
图5 螺母与滚柱啮合点位置Fig. 5 Meshing position of the nut and roller
式中,βnr表示滚柱与丝杠啮合处的牙侧角,即:
可通过滚柱与丝杠、螺母之间啮合点Qsr、Qnr位置坐标,得到轴向间隙分别为:
令滚柱与丝杠、螺母之间轴向间隙δsr、δnr均为0,并与式(20)~(23)联立,可以得到螺纹牙厚cs、cr、cn与丝杠、滚柱与螺母啮合点位置关系,从而实现三者之间无侧隙啮合.
1.3 齿轮副结构参数设计
根据PRSM 结构特征,得到PRSM 运动简图如图6 所示,其中,1 表示丝杠,2 表示滚柱,3 表示螺母,4 表示内齿圈,H 表示保持架.
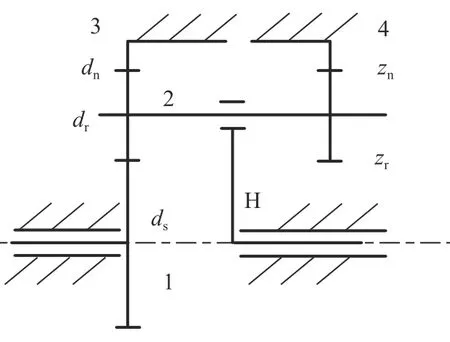
图6 PRSM 运动简图Fig. 6 Kinematic sketch of PRSM
从图6 中可看出,滚柱与螺母、丝杠螺纹啮合,同时与内齿圈齿轮啮合,得到滚柱端部轮齿中径与螺纹中径相等,因此,滚柱端部轮齿齿数:
式中,zr表示滚柱端部轮齿齿数,int 表示取整,m表示模数.
内齿圈齿数为:
式中,zg表示内齿圈齿数.
由于滚柱端部轮齿大径与螺纹大径存在不相等的情况,需要将轮齿进行变位,并且与内齿圈啮合点位置不变,因此,轮齿变位系数:
式中,ha表示轮齿齿顶高系数.同时,内齿圈变位系数为:
2 乌鸦搜索算法
乌鸦搜索算法(Crow search algorithm,CSA)[22]具有寻优速度快、控制参数少、使用灵活、结构简单等优点,已成功应用于工程优化设计、图像分割、径向分布网络中导体最佳尺寸的选择等实际优化问题.故本文将乌鸦搜索算法作为PRSM 结构参数优化算法.
CSA 算法原理如下:
(1)首先在可行域中随机生成种群位置,每个种群个体可用如下公式表示:
式中,d表示个体维数,xp-max、xp-min表示个体第p维上、下界,p=1,2,...,d,R表示[0,1]之间的随机数.
(2)产生新位置,乌鸦i会随机地在种群中选择一只乌鸦进行跟踪(假设选择被跟踪的是乌鸦j),如果乌鸦j不能发现被跟踪,那么乌鸦i就会偷走乌鸦j的食物;如果乌鸦j意识到被跟踪,用随机位置来骗取乌鸦i.乌鸦i位置更新公式如下:
式中,xi,iter+1表示乌鸦i的新位置,iter 表示迭代次数,ri表示取0~1 之间均匀分布的随机数,fl 表示乌鸦i的飞行高度,xj,iter+1表示乌鸦j在迭代过程中的位置,pi代表乌鸦j发现被乌鸦i跟踪的概率,pj,iter表示在迭代时乌鸦j感知概率.
(3)检查位置并更新.将乌鸦i新位置与当前位置进行比较,若新位置可行则更新;否则乌鸦i停留在当前位置.
(4)根据目标函数计算新位置的适应度值.
(5)更新乌鸦的记忆.如果新位置的适应度值优于原来记忆的适应度,则根据新位置更新记忆;否则不更新记忆.
(6)若达到最大迭代次数,搜索结束,反之,跳转至(2)直到最大迭代次数.
3 行星滚柱丝杠优化模型
3.1 假设条件
根据PRSM 结构特点,可做如下假设:(1)滚柱上螺纹牙载荷均匀分布;(2)多个滚柱承载均匀;(3)不考虑零件间的摩擦力;(4)不考虑PRSM 各类误差的影响;(5)丝杠、滚柱、螺母都是右旋.
3.2 优化变量
本文主要针对PRSM 中丝杠螺纹部分参数、滚柱螺纹与端部齿轮参数、内齿圈参数和内螺母中螺纹参数作为优化变量.丝杠螺纹中径ds,丝杠头数ns,导程ls,内齿圈模数m,宽度B,螺母外径与内齿圈大径距离dng,滚柱与丝杠、螺母螺纹牙接触对数e.
3.3 约束条件
(1)结构约束.
滚柱均匀布置在丝杠和螺母中间,由于其尺寸的限制,滚柱个数也会受到影响.图7 表示滚柱安装示意图,其中,α表示两相邻滚柱中心与丝杠中心所成直线的夹角.
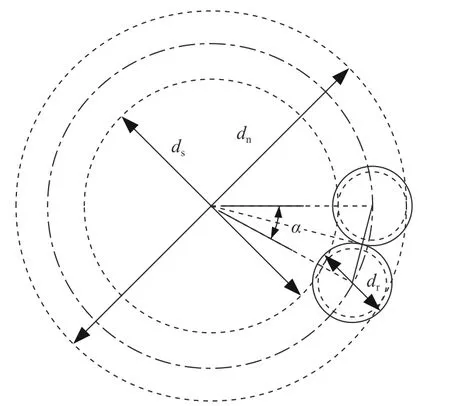
图7 滚柱安装示意图Fig. 7 Schematic of the roller installation
为了防止在安装过程中,相邻滚柱之间发生干涉,必须满足:
因此,滚柱个数为:
(2)强度约束.
对滚柱进行静力学分析,如图8 所示,忽略由于滚柱与丝杠、螺母啮合点位置对受力分析的影响,同时不考虑螺纹载荷不均的影响,可以用一个合力替代多个螺纹点上接触力.图8 中,Fgx、Fgy分别表示滚柱端部轮齿与内齿圈啮合时产生的径向力和周向力,Fnx、Fny、Fnz表示滚柱与螺母啮合时产生的径向力、周向力以及轴向力,Fsx、Fsy、Fsz表示滚柱与丝杠啮合时产生的径向力、周向力以及轴向力.

图8 滚柱受力图Fig. 8 Force diagram of the roller
根据滚柱受力平衡,可得到其在三个方向上的平衡关系,即:
考虑螺母在工作过程中只有轴向负载,并且多个滚柱间均匀承载.因此,可以得到每个滚柱承受轴向载荷为:
式中,F表示螺母承受轴向载荷.
结合式(19),可以得到螺母对滚柱作用的正压力为:
同理可以得到丝杠作用在滚柱上正应力为:
针对丝杠、滚柱以及螺母螺纹采用剪切、弯曲强度进行校核,根据螺纹结构形式,得到螺纹上剪切应力为:
式中,ao代表丝杠、滚柱以及螺母螺纹全齿高,o可以为s、r 或n,Fto表示丝杠、螺母作用在滚柱上正压力,e表示滚柱分别与丝杠、螺母接触螺纹牙数.
螺纹弯曲应力为:
滚柱端部轮齿进行接触强度、弯曲强度校核,得到轮齿接触应力为:
式中,K表示载荷系数,Fg表示轮齿上名义载荷,b表示轮齿接触宽度,m表示模数,YFa表示载荷作用于齿顶时的齿形系数,YSa表示载荷作用于齿顶时的应力修正系数,Yε表示齿根弯曲疲劳轻度计算的重合度系数.
由于滚柱端部齿轮被螺纹所切,所以其有效齿宽:
轮齿弯曲应力为:
式中,u表示传动比,ZH表示节点区域系数,ZE表示弹性影响系数,Zε表示齿面接触疲劳强度计算的重合度系数.
此外,对螺母进行拉压校核,从而确定螺母外径尺寸.
式中,dno表示螺母外径,为:
式中,hg表示齿顶高系数,cg表示顶隙系数.
3.4 目标函数
考虑到PRSM 整体体积最小,并且满足结构强度要求,同时各零件间不会发生干涉,应使螺母外径最小,丝杠中径最小,滚柱长度最短,因此,优化适应度函数为:
3.5 优化过程
PRSM 结构参数优化过程如图9 所示.

图9 PRSM 结构参数优化过程Fig. 9 Structural parameter optimization process of PRSM
(1)确定CSA 优化参数,PRSM 结构参数范围.
(2)对PRSM 优化参数随机初始化,并结合PRSM 结构约束条件和强度条件确定其余尺寸,并获取种群中每个个体适应度值.
(3)更新种群个体,并实现PRSM 每个结构参数更新.
(4)检查更新后的结构参数是否满足约束条件,如果不满足,则不更新其结构参数,并对更新后的个体计算其适应度值.
(5)对比更新前后个体适应度值,当更新后个体适应度值优于更新前的,用更新后的个体代替更新前个体.
(6)迭代次数达到最大迭代次数,更新停止,对比种群个体适应度值,从而获得最优的个体,实现PRSM 结构参数最优化设计.
4 实例验证
为了验证本文提出PRSM 优化设计方法的有效性.基于上述方法,首先,对优化参数分别设置范围,丝杠螺纹中径ds范围为[5 mm,100 mm]并为整数,丝杠头数ns范围为[3,6]并为整数,丝杠导程ls(单位mm)范围为{1,2,3,4,5,6,8,10,12,15,18,20,24,25,30,36},滚柱端部轮齿模数m(单位mm)范围为{0.2,0.25,0.3,0.6,0.8,1,1.25,1.5,2,2.5,3,4,5},滚柱端部轮齿宽度B(单位mm)范围为[3,20]并为整数,螺纹牙个数e为范围为[10,70]并为整数,滚柱螺纹牙厚cr的范围为(P/2,P).同时设置种群个数为50,迭代次数为1000,飞行高度为1,被跟踪概率设为0.5.PRSM 螺纹截面牙型角为45°,材料选择GCr15,材料属性如表1 所示.
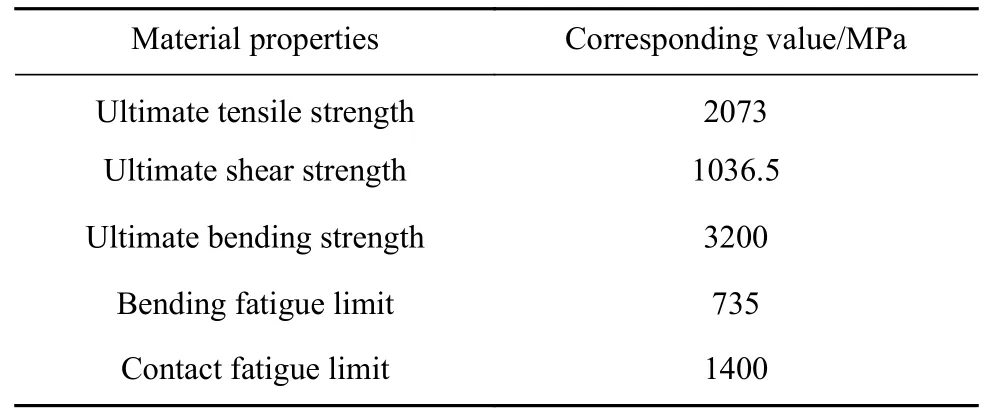
表1 PRSM 材料属性[23-24]Table 1 Material properties of PRSM[23-24]
根据国外产品手册[25],在推力0~100000 N、100000~200000 N 以及200000 N 以上三个范围中随机选取三种工况负载,分别为51000、102100、221600 N,利用本文提出的方法得到PRSM 结构参数如表2 所示.通过与国外产品手册进行对比,本文优化后PRSM 外形结构参数与国外设计的参数基本一致.本文方法所得到的螺距和螺母外径与国外设计的有一定偏差,主要是由于国外设计不同螺距下的PRSM 承载差别不大,在相同的负载下可以选择不同螺距的PRSM.
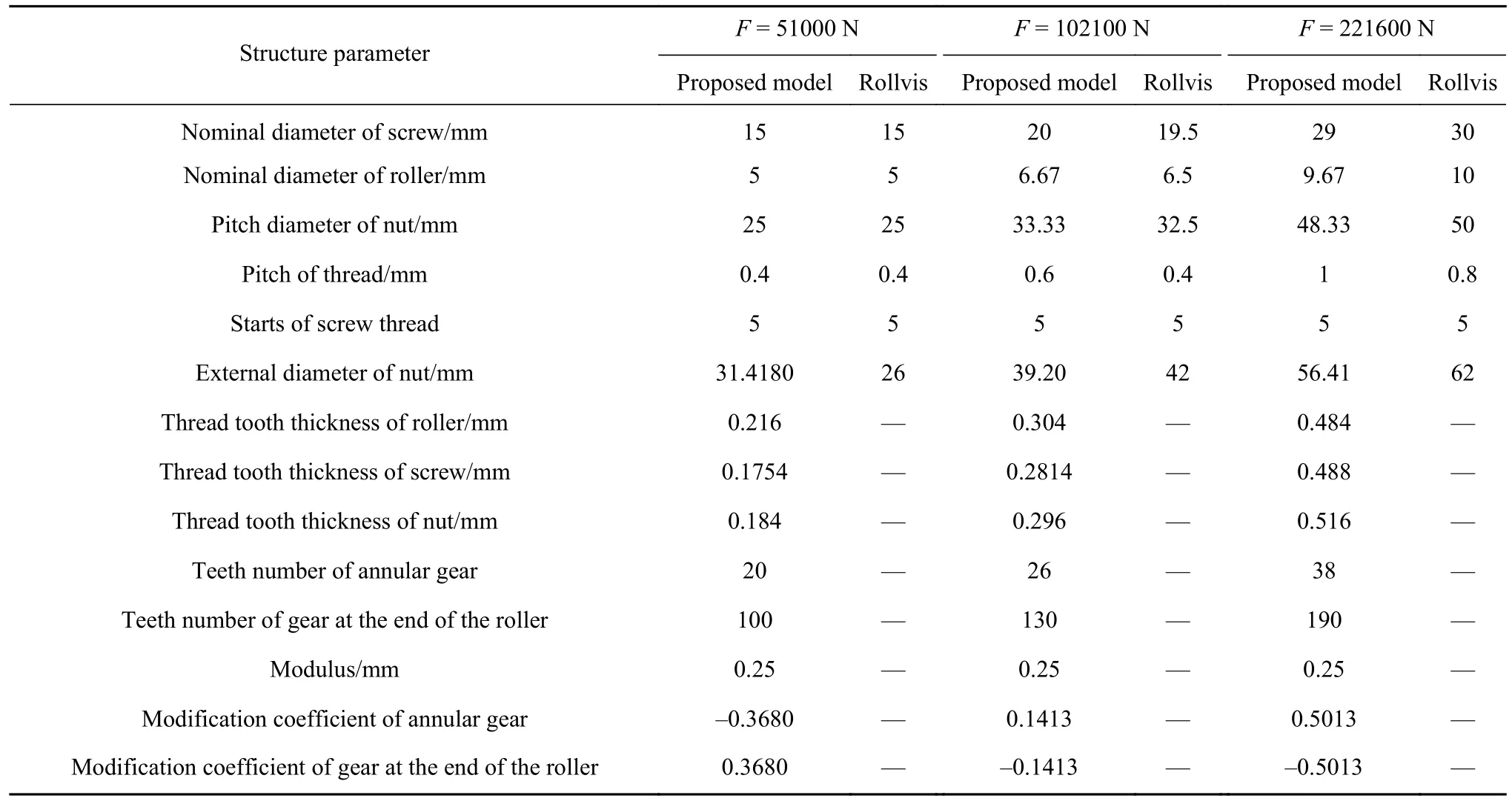
表2 PRSM 结构参数对比Table 2 Comparison of PRSM structure parameters
5 结论
本文针对现有PRSM 结构设计研究中没有同时综合考虑PRSM 螺纹副和齿轮副结构参数优化问题,建立PRSM 螺旋曲面方程,得到螺纹啮合侧隙与结构参数之间关系,通过调整螺纹结构参数实现PRSM 无侧隙啮合,同时,考虑螺纹结构强度及滚柱端部轮齿结构强度的影响,分别对优化过程中滚柱、内齿圈、丝杠、螺母等主要承力构件进行校核,从而保证优化后的PRSM 满足强度设计要求.然后以丝杠螺纹中径、头数、导程、滚柱端部轮齿模数以及滚柱端部轮齿宽度等为设计变量,以螺母外径最小、丝杠中径最小、螺距最小、导程最短、滚柱中径最小为优化目标,利用乌鸦搜索算法,建立PRSM 结构参数优化模型.最后根据以负载51000、102100、221600 N 为例,利用本文提出的优化模型进行结构参数设计,结果表明得到的结构参数与国外PRSM 产品手册设计基本一致.

