非常规油气藏多场耦合渗流理论研究进展

朱维耀，陈 震，尚新春

北京科技大学土木与资源工程学院，北京 100083

随着常规油气田的产能逐渐下降，非常规油气藏的开发成为针对未来巨大能源需求供给的重要新兴课题[1].在我国，非常规油气藏的范围包括页岩油气藏、致密油气藏、煤层气藏、油页岩等多种资源类型，在国外还将稠油、油砂、天然气水合物等也纳入非常规油气藏的范畴[2].这类油气藏被广泛开发主要归因于水平井钻探和大规模水力压裂（压裂）技术的进步[3].尽管已有不少成功的开采案例，但其产量的准确预测仍具有很大的不确定性，这种不确定性源于多物理场耦合作用所导致的渗流场非线性特性加剧[4].因此，多场耦合问题是研究非常规油气藏开采的一项重要科学问题.以往对多场耦合理论的运用存在简易化和适应性缺陷，工程中缺少理论指导下的开采工艺与开发方法，制约着这类油气藏的大规模高效开发，亟需对多场耦合渗流力学理论进行深入认识.

油气藏的多场耦合是指地下储层中温度场-渗流场-应力场（Thermal-hydrological-mechanical,THM）的相互作用[5]，是岩层复杂条件中真实行为的抽象反映，是由固体力学、渗流力学、传热传质学等众多工程学科相互交叉而形成的一门边缘学科[6-9].非常规油气藏开采过程中的多场耦合作用理论与工程问题的核心是不同物理场对非均质、非线性渗流场的作用和影响[10]，对这种影响的实验验证、理论描述及数值模拟是研究中的重点[11]，具体包括应力场变化对储层渗流条件的影响、温度场变化对渗流条件的影响、多场耦合作用对流体特性的影响，以及各物理场的理论模型之间如何进行耦合和对应的解耦、求解等问题，这些问题的解决都可为现场生产提供重要的理论、工程指导[12-15].

本文旨在了解非常规油气藏开发过程中多场耦合问题的研究现状与发展前景，提出了当前多场耦合渗流力学理论发展所面临的关键问题，针对数值模拟技术的现状、进展和瓶颈进行了探讨，并对多场耦合渗流力学理论及应用的未来发展提出了展望.

1 非常规油气开采多场耦合作用机制

非常规油气藏的流体行为表现为多尺度多相流体（油、气、水）在超低渗透、高度非均质而且强应力敏感的孔隙-裂缝介质中流动.与常规油气藏流动相比，多场耦合作用更加显著，造成高度非线性和复杂的流动过程，并且伴随剧烈的岩石-流体相互作用，以及纳微米孔隙及微裂缝的变形[16-19].随着岩石力学多物理场耦合试验以及各种现代化无损探测手段的发展，对非常规储层在热-流-固多场作用下的微观演化过程和结构变化的研究逐渐细化，可通过室内实验量化地研究流固耦合作用、温度的变化、有机质特性的变化对流体流动行为的影响规律等[20].

1.1 应力场演化对渗流场的影响

应力场演化对渗流场的影响通常采用岩石固有渗透率的变化来表征.在常规油气藏中，应力场的变化对岩石变形和流动能力的影响一般较小，在实践中大多会被忽略[20].但在非常规油藏中，应力场的变化所引起的渗透率变化将显著得多[21].通常认为，开采过程中流体压力的快速下降将导致有效应力（总应力与流体压力之差）的上升，进而使岩石进一步被压实并减小孔喉尺寸、减弱孔隙的连通性，因此降低渗透率.这一特性也被称作渗透率应力敏感性.研究者们通过将高温高压条件下的三轴试验系统与岩心流动实验相结合，测试流固耦合作用下深部岩心的流动能力[22]，并发现基质岩心的表观渗透率会随着有效应力的增大而降低，降低幅度可以达到30%～99%[23-27].一方面，黏土矿物的含量越高，应力敏感性越显著[28]；另一方面，非常规油气藏中大量的烃类物质吸附在有机质的表面，一旦流体压力降低，烃类物质几乎立即解吸[29]，导致吸附应变[30]，宏观表现为基质骨架被压缩、渗透率升高[31].不过，矿物含量和吸附对固体变形的影响相对较小，在大多数理论研究中都被忽略.

渗透率的应力敏感性强度受储层致密性的影响最大.笔者团队曾对巴西劈裂实验进行改进，利用单轴试验机缓慢施加载荷，可以在不破坏岩心整体构型的情况下，得到人造微裂缝（图1），从而对不同条件的非常规岩心进行应力敏感性测试[32].发现当有效应力从4 MPa 增至22 MPa 时，基质岩心和裂缝岩心的渗透率下降幅度平均分别为95.5%和85%（图2），即基质的应力敏感性相对更强.为了在理论层面对基质和裂缝进行分别描述，多数研究者采用了多重介质和离散裂缝模型[33].

图1 裂缝性岩心的CT 扫描Fig. 1 CT scan image of a fractured core

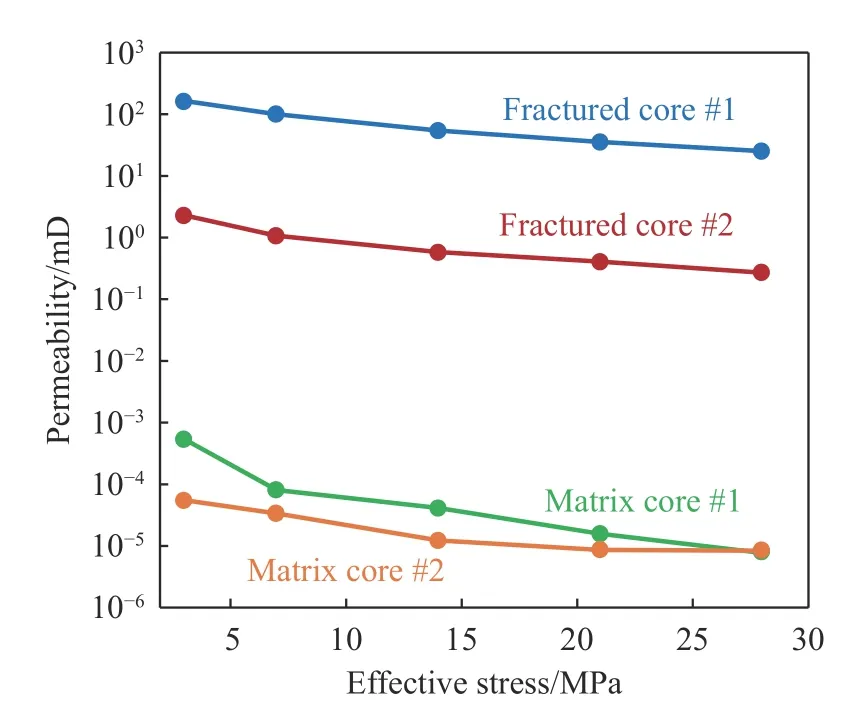
图2 基质和裂缝岩心的应力敏感性测试Fig. 2 Stress-sensitive experiment of matrix and fractured cores

影响渗透率应力敏感性的主要因素还包括微观孔道结构.对非常规储层的压裂改造将起到对微裂缝连通的作用，形成复杂的裂隙网络，这使得应力演化及应力-应变关系变得复杂，因为在有效应力的持续作用下，支撑剂可能被压实，甚至可能发生压碎，使裂缝闭合，导致不可逆的渗透率损失，岩石存在塑性变形行为[34-35].裂缝表面粗糙度越高，支撑能力越强，应力敏感性越弱.不过，对地下真实裂缝的表面粗糙度进行评估还是一项巨大的挑战；而且，在数值模拟过程中应用不同的应力敏感数学模型将对数值计算结果产生明显的影响，因此，如何从物理基本规律出发实现应力敏感量化评价是亟待解决的问题.

值得注意的是，室内的物理实验往往无法真实还原地下条件，这可能导致实验上的误差.特别是非常规油气藏的渗透率比常规储层小3 到6 个数量级，这使得这类油气藏的渗流实验非常耗时，也并非所有常规实验都适用于非常规储层的测试[36-37].未来研究的重点应在如何在实验室中精确模拟地下的真实应力环境和流动条件.

1.2 温度场变化对渗流场的影响

非常规油气藏储层的温度大都比常规储层高，比如我国龙马溪组页岩气藏的温度可达150 ℃左右[38].在非常规油气藏开采时必须进行水力压裂，这一过程可能会将多达两万至四万吨水被注入地下[39]，与储层发生能量交换.在常规油气藏理论中很少考虑能量转化效应，但在非常规油气藏开采过程中是必须考虑的.

首先，在非常规油气藏中，岩石随着温度的变化而发生热胀冷缩，这一效应对流动空间结构的改变将是很显著的[40]，固体骨架热膨胀导致孔隙和裂缝系统空间的减少，从而导致渗透率的降低[41-42].其次，有机物是非常规油气藏的重要组成部分，随着热成熟度的增加，有机质发生热解，析出原油、天然气，增加岩石孔隙的体积以及流体压力[43-44].还有研究表明，温度上升所造成的烃类物质解吸量增大也会导致岩石形变[45-47]，然而，烃类吸附为放热过程、解吸为吸热过程，因此发生解吸的位置储层温度将下降，反过来降低解吸量.研究人员必须通过分子动力学等微观方法计算宏观量化指标，如吸附热[48]、吸附等温线的交叉点[49]等.对烃类吸附以及置换过程中的热量转换和传输以及对物理场的影响机制还有待进一步的量化研究.

此外，还必须考虑温度的变化对流体黏度、密度的改变，特别是重质油，其黏度及密度随生产环境温度变化的范围可能很大[50].多种复杂的机理共同作用，导致目前对发生热解后的岩石孔隙结构的表征是非常规油气藏开发的主要挑战之一[51-52].现有研究通过一种或几种方法表征部分尺度的孔隙空间随温度场的变化规律，如通过微观CT 扫描技术来研究岩心加热过程中的微米级裂缝和黏土矿物的演变[53-55]，通过扫描电镜来观察岩石孔隙的形态变化并划分分布、类型[3,56]，以及通过气体吸附实验对岩心样品的孔隙结构进行分析[57].然而，因为缺乏有效而可靠的方法来综合量化地比较使用不同方法获得的多尺度数据，目前很少有关于温度与多尺度孔隙之间综合比较的研究.应当将这一问题作为下一步的研究方向，以期对温度场的影响有更加全面的认识.

2 非常规油气藏多场耦合作用理论模型

如上节所述，非常规油气藏的储层条件差，渗流场与应力场、温度场耦合作用，流体的流动更为复杂，这就需要一套完整、精确的多场耦合作用理论，针对各个物理场建立多组偏微分方程（PDE），以通过不同流动区域中的动态物性模型来定义油气的开采过程，从而区分不同区域之间以及多种物理场之间的相互作用.

2.1 应力场的控制方程

满足非常规油气藏的应力场控制方程可以通过扩展已知的多孔介质的本构方程（应变和应力之间的关系）来获得[58]，并由此得出固体质点位移方程来描述介质的变形.储层机械行为通常被大多数研究假设为各向同性及弹性形变，再从基于Biot 原理的孔隙弹性理论和双重介质理论出发，通过基质和裂缝的混合系统来描述机械变形的过程.当页岩或致密油气藏投入开发后，孔隙及裂缝压力降低，原始底应力场发生改变，有效应力增加，不仅使岩石骨架受到压缩，也使固体质点发生位移.通常近井地带的位移较大，但随着时间的增加，这种位移逐渐向远井地带推移，这种随时间变化的推移用固体静力学变形方程进行描述.被广泛采用的油气藏储层变形控制方程如式(1)所示[59-61]：

其中，εij是总的应变张量；G是岩石的剪切模量，Pa；KV是岩石的体积模量，Pa；σij表示岩体的应力张量，Pa，i和j分别取1～3；σkk为岩体在三轴方向的法向应力之和，Pa，σkk=σ11+σ22+σ33；δij为克罗内克（Kronecker）函数，当i=j时，函数取1，否则等于0；αm和αf分别为基质系统和缝网系统的Biot系数，根据岩心力学实验测得[62-63]；pm和pf分别为基质系统和缝网系统的孔隙压力，Pa；εd为吸附引起的体积应变.

剪切模量G和体积模量KV可通过下式计算[64]：

其中，E是岩石的弹性模量，Pa；ν是岩石的泊松比.

非常规油气藏所特有的吸附-解吸行为应在应力场方程中加以考虑.通常，吸附被假设为仅发生在非常规油气藏的基质中，εd表示为如下的Langmuir 形式[61]：

其中，εL是Langmuir 吸附应变；pL是Langmuir 压力常数，Pa.

通常，开采过程中的固体力学问题被考虑为静力学问题，此时满足动量守恒方程：σij,j+Fi=0.其中σij,j表示应力 σij在j方向上的一阶偏导数.将动量守恒方程以及应变-位移几何关系εi=引入式(1)，即转化为以位移为待求量的偏微分方程组：

其中，ui,j代表位移ui（单位m）在j方向上的一阶偏导数；ui,jk代表位移ui（单位m）在j和k方向上的二阶偏导数；Fi为体积力，在力学问题中通常是物质的重力，Pa.

当考虑渗流场的影响时，应力场控制方程(4)压力pm及pf均下降，烃类物质的解吸量增加，固体应力的方程不再平衡，于是固体质点发生位移，位移量的大小与压降程度有关，位移的方向指向压降最严重的区域.

当考虑温度场的影响时，在方程(4)中还应增加线热弹性形变项：KVαTTi，以表征温度变化导致的固体热胀冷缩.其中 αT为线热弹性应变系数，K-1；Ti为温度T（单位K）在i方向上的一阶偏导数.

不过，上述模型中仅考虑了固体具有弹性应变，而地下的岩石往往在具有弹性应变的同时还具有塑性应变，但目前考虑固体塑性应变的模型并不多见，因为地下岩石的塑形变形是很难观测的.此外，应力场的变化还不仅由于生产所导致，针对非常规油气藏的水力压裂以及生产过程中的重复压裂都会使原有应力环境发生改变，如使最大主应力方向发生变化[65-66]、改变固体力学参数、裂缝延伸扩展的模式发生转变[67]等.这些复杂的因素都应在未来的多场耦合研究中详加考察并细致计算.

2.2 渗流场的控制方程

非常规油气藏的渗流具有非线性特性，其渗流控制方程基于质量守恒原理.多孔介质（孔隙、裂缝）中多相流体（原油、天然气、水）的存储与流动都用一般的渗流控制方程来表征：

其中，t表示时间，s；ρ表示流体在t时刻的密度，kg·m-3；v表示流体在t时刻的流速，m·s-1；q为质量源汇项，kg·s-1；m表示单位多孔介质体积中的流体质量，kg，在非常规油气藏中，此项包括游离相和吸附相[68]：

其中，ρ和 ρsc分别为烃类物质在储层和地面条件下的密度，kg·m-3；φ为多孔介质岩体的孔隙度；ρr为多孔介质岩体的密度，kg·m-3；p为流体压力，MPa；VL为Langmuir 体积常数，m3·kg-1.

非常规油气藏的非线性渗流特征体现在运动方程上.对于常规油气藏，流体的速度v按达西定律的形式，表现为与有效渗透率K成正比的关系.然而，非常规油气藏的流动孔径为纳米级，流体流动受纳微米效应的影响显著，实测流量与线性达西定律（流速v与多孔介质渗透率K成正比）[69]的理论值存在偏差，因此通常采用表观渗透率Kapp（m²）来表征有效的渗透率[70].非常规油气藏与常规储层中的流动条件和输运机理存在许多区别，渗流控制方程中必须整合处理流动的主要机制，包括吸附、努森扩散、渗流，以及温度和压力对流体物性的影响等[71-72].在一些合理假设下，裂缝及大孔隙中的流动通过线性达西定律进行描述，而纳微米孔隙中的流动则必须考虑各种流动机制耦合影响[73-74]，在多场耦合条件下被采用得最多的流动模型是Beskok 和Karniadakis[75]所建立的纳微米通道传输方程（B-K 模型）：

其中，v为烃类物质的流动速度，m·s-1；µ为烃类物质的黏度，Pa·s；Kr为相对渗透率；Kapp为烃类物质流动的表观渗透率，m2；Keff为储层变形时的固有渗透率，m2；α和b为实验室所测得的参数；Kn为多孔介质流道的努森数，其表达式如式(8)所示[76]：

其中，λ为平均分子自由程，m；r为特征长度，在多孔介质中为孔隙半径，m；KB为玻尔兹曼常数，J·K-1；rc为分子碰撞有效直径，当考虑单一成分的分子时，等于分子直径，m；φeff为储层变形时的固有孔隙度；τ为多孔介质的迂曲度.

从而，Kn的变化蜕化成为一个与φeff和Keff相关的量；其余的量可视为定值，或由实验数据测得其随温度、压力的变化情况.方程(7)是对线性达西定律的非线性修正，一些研究报道了与方程(7)的形式不一致的流动模型，这些流动模型多采用渗流阻力代数和的形式，但也采用了表观渗透率的表述形式，不过大多形式复杂、参数繁多，关键是大多仅有实验室尺度下的流动模拟案例，而不能应用于储层宏观理论的问题.具体可参阅Akilu 等[77]及Taghavinejad 等[78]的论文.

当考虑应力场的影响时，储层骨架质点发生位移，整体发生应变，方程(6)中的孔隙度 φ随应变的增加而降低，方程(7)中的渗透率Keff随孔隙度的降低而减小，从而流体流动能力减弱、流量减小.因此，储层降压开采的同时流动条件会变差.有多种模型描述这种介质渗流能力的变化，见本文2.4 节.

当考虑温度场的影响时，流体的密度ρ、黏度µ以及吸附量都将随温度的变化而改变.温度越高，流体的密度、黏度越低，吸附量越小，因此渗流能力随之增强、流量增大.反之亦然.

目前国内外非常规油气藏实际案例开始实施CO2置换等提高采收率办法，但截至目前，仍缺乏一种行之有效地对混合流体的流动行为进行描述并得到充分验证的输运方程式.而且，非常规储层中高温、高压条件下的流体相态变化也可能造成流动条件的改变，尽管这一影响可能很重要，但目前还没有一种综合的方法来计算多组分流体在相变条件下的流动.这是未来值得研究的问题.

2.3 温度场的控制方程

温度场的演化可依据油气藏能量方程来获得.尽管同一个体积空间中共存着岩石骨架与流体，而且热力学的特性不同，但依据温度场作用普遍的基本假设：每个时间步中的热量变化在瞬时完成，可将不同物质的热力学参数（如导热系数、热容等）作为等效的物理量，构建能量守恒方程[79].其典型形式如式(9)所示：

其中，λc为岩石骨架与流体的等效导热系数，W·m-1·K-1；T为温度，K；Qst为单位摩尔吸附流体的吸附热，J·mol-1；ρdsc为可吸附烃类物质的地面条件密度，kg·m-3；Md为可吸附烃类物质的摩尔质量，kg·mol-1；Vd为当前条件下单位体积岩石的吸附量，m3·kg-1；ηc为骨架与流体的质量等效热容，J·kg-1·K-1，其等效计算方法为：

其中，cr、co、cw、cg分别为岩石、油、水、气的热容，J·kg-1·K-1；So、Sw、Sg分别为油、水、气的饱和度；ρo、ρw、ρg分别为油、水、气在地下条件下的密度，kg·m-3.

通常，烃类化合物的吸附/解吸造成的热量转换使非常规储层的温度场发生变化的幅度并不大，仅有近井地带由于解吸量较多，才导致发生一定的温度降低[80]，通常可以忽略.但是，现在采用新型压裂和开采工艺的案例逐渐受到关注.如无水液氮压裂[81]、超临界CO2压裂[82]、电磁加热开采[83]、微波加热开采[84]等.这些新工艺和新技术在实施过程中，都面临着显著的温度场大幅变化，通过多场耦合理论来准确评估和预测这些过程是非常有必要的.

当考虑渗流场的影响时，方程(9)中需要增加对流传热项，当考虑油、水、气三相流动时，对流传热项为：

其中，vo、vw、vg分别为油、水、气的流速，m·s-1.

该项保证了流体能借助传输过程将热量传递到相邻网格之中.流体的对流传热方向指向射孔位置，射孔位置是烃类解吸吸热程度最大的位置，因此对流传热能够降低储层的温度降低速率.

2.4 渗流-应力-温度三场耦合模型

对多种物理场相互作用、影响的模型进行理论建模并联立求解即为全耦合模型.方程(4)、(5)、(9)彼此独立，联立之后就构成了非常规油气藏中热-流-固（THM）耦合模型的基本非线性物理过程，也是求解这一复杂过程的应力、压力以及温度等物理量变化规律的基本方程形式.单独的方程组较为理想化，各物理场之间的方程是独立的，而一套完整的非常规油气储层的模拟器必须考虑各个物理场之间的参数影响，需要准确关联不同流动和传输机制，将多物理场耦合在一起.物理场彼此之间的密切联系如图3 所示，整个过程是动态且依赖时间的.

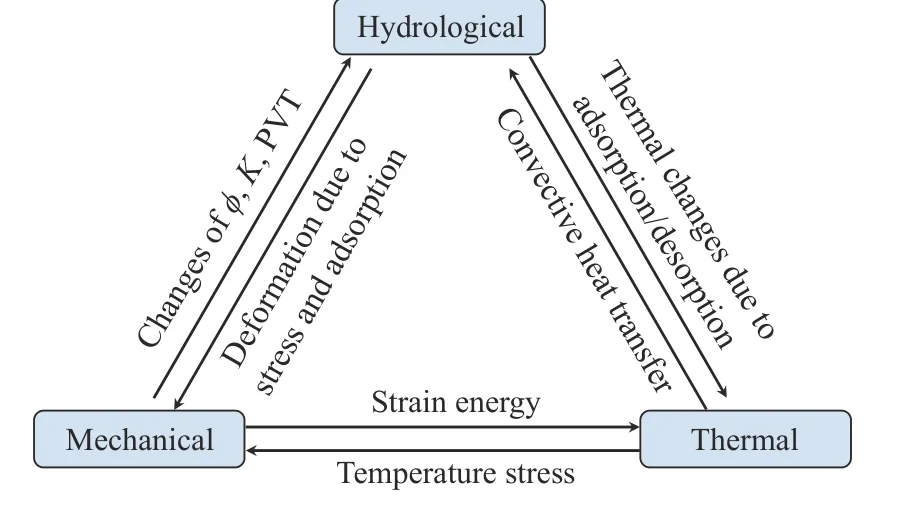
图3 非常规油气的多物理场之间的相互作用Fig. 3 Interactions between multiphysical fields in unconventional oil and gas reservoirs

（1）全耦合对渗流场的影响.

全耦合对渗流场的影响主要包括对渗透率和流体物性的影响.固体的渗透率受岩石形变的影响.根据岩石力学建立有关表征Keff的本构方程，在多场耦合的研究中，被广泛采用的本构方程是三次法则[85]：

其中，K0是储层未发生变形时的初始渗透率，m²；φ0分别为储层未发生变形时的孔隙度.从而，Keff的变化问题又蜕化为φeff的变化问题.基于孔隙度变化量与固体应变量的几何关系，一些描述孔隙度-应变的本构模型已被提出并被用于应力敏感岩石变化特性的实验验证[86-89].本团队博士亓倩对岩石骨架和孔隙的弹性模量进行了研究，发现在前者远大于后者的情况下，基质应变远小于孔隙体应变，可以仅考虑孔隙体变形，并建立了本构模型[90]：

其中，αp为有效应力系数.

式(11)和(12)描述的是基质内的孔隙度、渗透率的变化.不过非常规油气藏开采的关键是裂缝的导流能力，裂缝的表面粗糙度使裂缝能够实现自支撑，这种自支撑可以改变裂缝各向异性的渗透率[91]，这使裂缝介质与基质的演化存在区别.而且，非常规储层的裂缝有效流动宽度通常小于实际的裂缝宽度[92]，为裂缝应力敏感物理模型的推导带来难度.为此，现有研究大多采用经验公式，如通过在各种岩性上对裂缝的加载和卸载行为进行试验，从中得出裂缝的渗透率对应力演化响应的非线性关系[93].但是，现在还没有有效的监控地下裂缝表面粗糙度的手段，这是未来应予考虑的问题.

流体物性受压力和温度的双重作用，对其进行数学描述是一项挑战.至今还没有足够精确同时方便计算调用的光滑的数学模型，只能通过经验公式进行描述，并在一定压力、温度范围内保证结果的精确性[94].在笔者的所做研究中，收集并调用了流体高压高温物性的数据库，避免了使用任何经验公式[80].采用这种方法比经验公式准确得多.

（2）应力场和温度场的相互作用.

应力场和温度场存在相互作用.主要体现在温度的变化使固体产生热胀冷缩的热应变，而固体的形变对温度场产生应变能.应力场的控制方程中应增加热应变项：

其中，εQ为热应变，Pa.

同时，温度场的控制方程中应根据应变能的计算方法增加附加热源：

其中，εV为当前时间步中的固体应变.

由此，才能形成满足图3 所示的方程耦合关系.这就是非常规油气藏的全耦合基本模式.全耦合的计算需要联立求解三个物理场的所有物理量，尽管准确性高，编程非常复杂繁琐、耗费硬件资源，而且时间步长必须控制在很小的范围内以保证收敛.为此，研究人员们也通过半耦合模式来作为全耦合的替代.

2.5 渗流-应力二场耦合模型

绝大多数情况下，非常规储层仅采用天然能量开采，而不采用热采或化学开采工艺，此时温度场的影响相对较小，特定情况下可以忽略不计[80]，没有必要计算渗流-应力-温度三场耦合，计算渗流-应力二场耦合模型即可.因此，耦合模型仅包括渗流场和应力场两种物理场的控制方程，应力的变化是储层渗流变化的绝对主导因素，也被称为储层的应力敏感性.

根据弹性力学，应力场的控制方程通过有限元法进行求解.但是，渗流场的控制方程大都利用有限差分或有限体积法求解.由于有限元法的网格与求解渗流场的网格（结构化网格或非结构化多边形网格）不一致，所以在每个时间步计算过程中必须更换网格，所有数值在更换网格时均需要插值.为了避免频繁更换网格所增加的不稳定性，可选择两种解决方案.其一是渗流场也通过有限元法来求解，如使用商业软件COMSOL；其二是简化流固耦合过程，为此研究者们开发过许多经验公式来描述渗透率随压力变化的关系，如最普遍的幂指数模型[61]：

其中，K0为初始渗透率，m²；c为基质或裂缝的压缩系数，Pa-1；p0为初始压力，Pa；p为储层的实时压力，Pa.

由于非常规储层裂缝系统的复杂性，有时经验公式并不能完全拟合裂缝的渗透率或导流系数变化，但较为完整的实验数据可以作为数值计算的补充，模拟过程中对实验参数的直接调用往往是更加准确的方法.在未来必须面临的问题是对地下真实裂缝情况和行为的准确认识，特别是裂缝的自支撑作用对导流能力变化的影响，这可能与支撑剂的破碎性能及其在裂缝中的填充规律有关，但在目前的理论计算中这仍是一个巨大的挑战.

3 非常规油气藏多场耦合作用仿真模拟

对多场耦合过程进行模拟非常具有挑战性：首先，开发出一个功能齐全的模拟器来模拟所有复杂物理过程是很难的；第二，找到一个能满足理论上合理的解耦方法的本构关系需要跨学科的专业知识，而且目前没有通用的解决方案；第三，多场耦合仿真的模拟验证受到可以涵盖所有物理场演化过程的严格限制.因而，问题的非线性很强，除了少数特殊情况可求出解析解外，一般需要用数值方法进行求解.这就要求模拟方法满足与实际情况吻合的准确性、针对解耦过程的适应性和可接受计算速度.

3.1 模拟仿真方法

流固耦合模拟仿真始于20 世纪80 年代，最初在单相流动中得到实现[95].由于单相流的方程中少了相对渗透率、毛管压力等一系列非线性因素，大多数仿真能够以完全耦合的方式同时求解多物理场控制方程[96-97].多相流研究的重要性逐渐凸显后，人们开始寻求不同的解耦方法，以提高计算效率和精度.这些耦合计算方法可分为单向耦合、迭代耦合和完全耦合三种.

（1）单向耦合（半耦合）.

模拟器在每个时间步中，先执行渗流模拟计算，再将压力和饱和度解传递给应力场控制方程进行应力或位移的计算.这种方法也称为松散耦合，因为应力场的计算只接收流动解，而应力或位移解并不反馈给渗流场的计算.考虑温度场的情况也类似，即分别求解渗流场和应力场、温度场的三组方程[98-99]，也叫做半耦合.由于无需联立求解所有物理场的参量，而是分步、依次地求解每个时间步内的物理量，因此不是严格意义上的耦合，但是通过大量计算显示，在时间步长得到有效控制的条件下，半耦合模型的结果也可以达到全耦合模型的精度[100]，因此也被研究者们采用.

（2）迭代耦合.

每个时间步中，分别依次求解各个物理场控制方程中的主要待求量，也被称为顺序耦合.通常先求解渗流场控制方程，然后将压力和饱和度解传给应力场方程[101-102].应力场方程的解再传给到温度场以及渗流场的控制方程，直到所有方程在同一个时间步中收敛[103].这种方法在每个时间步中都是双向耦合的.这种方法实施起来较为简便，占用内存较小，运算效率较高，稳定性好，现今科研界被广泛应用的COMSOL 软件即采用顺序耦合.

（3）完全耦合.

将多个物理场的非线性偏微分方程在每个时间步中同时求解，一次性解得所有待求量.大多数完全耦合的仿真模拟仅限于单相流动[104].这种方法的计算精度最高，不过处理和计算较难，而且对内存和运算能力的要求都很高，任何微小的初始化设置失误都很容易导致计算不收敛.

除了上述常见的多场耦合研究外，还有一些研究者开发了适用于一定条件的半解析解耦方法.笔者基于非均匀全流场流固耦合参数的宏观数学表征方法，离散单元上引入近似Boltzmann 变换，建立一种半数值-半解析求解多场耦合过程的方法，计算速度远高于数值求解，可在一阶精度上解决非线性非稳态非均匀的渗流问题.

3.2 考虑多场耦合作用的非常规油气藏模拟

笔者在曾经提出的三大区、五小区的裂缝网络物理模型（图4）上进行多场耦合产能模拟研究，对于建立的非常规油气藏的水平井体积压裂非线性渗流偏微分方程及应力场、温度场的分区模型进行构建.目前的求解难点在于裂缝控制区缝网形态变化的数学描述，流固耦合计算过程需要对体积压裂的复杂缝网结构做理想化的处理，只能限制在弹性变形和较为简单的弹塑性变形以内，才能使用严格的数学公式对裂缝形态进行描述.为此，笔者基于平板渗流理论、树状分形理论来表征体积压裂复杂裂缝形态，分为树状、簇状、羽状、网状四种基本形态，从而求取其等效渗透率以及应力敏感变化[105].

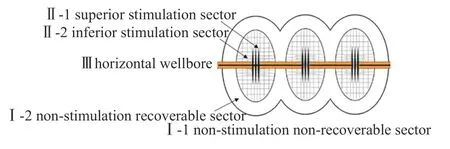
图4 “三大区，五小区”多尺度模型Fig. 4 Multiscale model of the “three main sectors,five subdivided sectors”

根据笔者所进行的多相多场耦合计算产量变化曲线，温度场变化主要受解吸附时温度降低的影响，下降幅度较小，影响相对有限；而应力场的变化对孔、渗的影响较大，流-固耦合作用对生产动态有相对更显著的影响.以非常规气藏为例，考虑多场耦合作用时产气量降低约13%（图5）.因此地质力学参数对产量的影响也较为显著，如弹性模量越大，岩层抵抗变形的能力越强，表现出比较弱的多场耦合作用；即弹性模量越大，储层刚度越大，流固耦合作用对流动通道的影响越小，累产气量、累产水量越大.并且，随着地应力的增加，岩石应变增强，孔隙度减小，产气、产水均下降.若不考虑压裂中应力差对改造效果的影响，生产过程中气井产能主要受控于最小水平主应力大小：最小水平主应力越大，地层流体采出后，裂缝所承受的应力伤害增加，累产气降低.

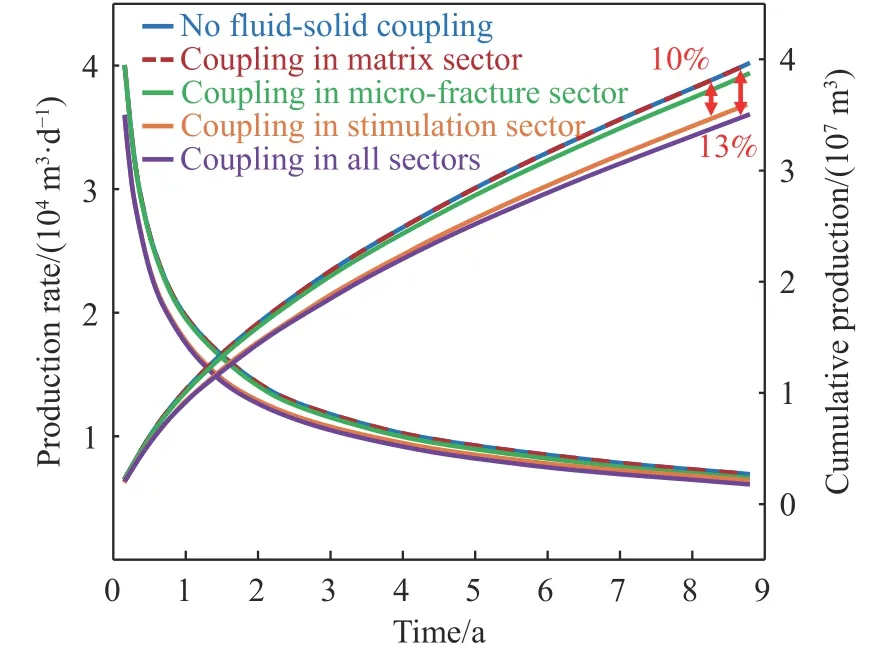
图5 多场耦合作用对多尺度流动区域的影响Fig. 5 Multiphysical fields coupling effects on multiscale flow sectors

现代计算机运算能力的飞速发展对通过数值方法高效和精确的求解提供了更大的可能性和前景[76].在阐述非常规油气藏流动和运移机理的基础上，相应的数学关系可能被更加精细地描述并形成高效能的模拟器.尽管目前已在描述单个机制方面取得了进展，但仍然缺乏能够以综合方式耦合大部分或所有机制的大型集成的油气藏模拟器.另一方面，在普通油气藏中考虑多物理场耦合问题会显著增加模拟器所需的计算成本.为了提高非常规油气藏模拟器的计算效率，需要研究可以进行分布式计算或云计算的高性能计算方案，并专门用于大规模非常规油气藏模拟.

4 结论与展望

对于非常规油气藏的多物理场耦合渗流理论和数值模拟的研究，由单相、线性渗流理论向多相、非线性、跨尺度、多物理场耦合计算发展，特别是在近年来非常规资源愈加受到重视的时期，新发现的资源大多为含有纳微米孔隙的非常规油气藏，由于目前均采用体积压裂后降压开采，流场受到应力场、温度场作用明显.建议对于室内试验中模拟地下真实应力环境、温度条件、烃类吸附及置换的热量变化等问题深入研究，深化对地下岩石的塑性应变、重复压裂过程中的应力环境变化、混合烃类的输运模型、以及孔渗随应力和温度发生变化的数学模型等问题的认识.依据所建立的适应性多场耦合模型，配合研究分布式计算或云计算的高性能计算方案，用于大规模非常规油气藏模拟.此外，笔者认为针对多场耦合渗流理论的研究，在继承前人研究结论认识的基础上，应在理论深度、大型化计算等方面进一步深化研究，使其推广到更多的领域.具体展望如下：

（1）深海油气资源开采：深水低温环境、地层强度偏低，采用大规模丛式井开采，井下设备磨损快.导致水下生产系统难建设，开发方案难制定.再加上低温条件下的烃类物质易形成水合物，导致管道阻塞.亟需结合多场耦合渗流力学，形成深海油气高效开发方法.

（2）水合物开采：水合物资源处在高压、低温、复杂相变的环境之中.不论是采用较为简单的降压开采、CO2置换，还是热采、化学开采等方法，涉及水合物分解相变与气-水在地层内渗流传热等多个物理化学过程之间的耦合机理都十分复杂，亟需建立水合物开采多场耦合渗流理论.

（3）替代稠油火烧油层工艺技术：通常对于蒸汽热采效果不好的稠油油藏，火烧油层是一种对稠油油藏的终极技术，会为储层带来许多不利影响，包括潜在的、不可逆转的化学作用.该工艺进行后，稠油储层即废置.亟需寻找可替代技术，高效开发热采效果不良的稠油，包括近年来的化学剂降黏、CO2降黏技术等，这个过程中所涉及的多场耦合过程亟需加以研究.还需在热物理化学方法上寻求变革性技术或新的突破技术，如核、控温近火烧油层、微波技术的安全利用，以及结合立体井轨迹与流场多区域适配控制技术等，并建立更加前沿的适应性多场耦合渗流力学理论.