基于主动迁移学习的电力系统暂态稳定自适应评估

李宝琴，吴俊勇，李栌苏，史法顺，赵鹏杰，王 燚

（北京交通大学电气工程学院,北京市 100044）

0 引言

在“双碳”目标［1］的引领下,大量的新型负荷接入电网,导致拓扑结构和运行方式频繁变化［2］,对系统的安全稳定运行构成了严峻的挑战［3］。

时域仿真法［4］和直接法［5］是传统的暂态稳定分析方法,但是随着电力系统规模和复杂度的急剧增加,传统方法难以满足现阶段在线应用的需求。

数据驱动的暂态稳定评估（transient stability assessment, TSA）方法通过离线挖掘测量数据和输出结果之间的映射关系,在线进行快速实时的TSA。早期基于机器学习的TSA 方法多局限于浅层学习,如支持向量机（support vector machine,SVM）［6］、决 策 树（decision tree,DT）［7］、随 机 森 林（random forest,RF）［8］和k近邻（knearest neighbor,KNN）［9］。随着深度学习的迅猛发展,研究者们对基于深度学习的TSA 方法进行了大量的分析和改进。文献［10］将深度置信网络（deep belief network,DBN）和TSA 相结合。文献［11］提出集成DBN 的框架进行多级TSA。文献［12］为了解决深度学习模型结构选择和评估性能优化等困难,提出一种两阶段TSA 方法。文献［13］提出了基于多任务学习的TSA 模型,实现了功角稳定和电压稳定的同步评估。文献［14］为了充分挖掘电力系统TSA 过程中的时序数据,提出一种基于改进一维卷积神经网络（convolutional neural network,CNN）的TSA 方法。文献［15］借助长短期记忆（long short-term memory,LSTM）网络输出结果的时序特性,提出一种基于样本关注度与多层次特征的多阶段电力系统TSA 方法。文献［16］引入数据空间可靠域的概念,采用多智能体互补模型进行TSA。

但是上述方法假设测试样本和训练样本独立同分布,一旦电力系统的拓扑结构和运行方式发生较大变化,该假设难以成立,导致预训练模型性能受到极大影响。迁移学习［17-18］凭借收敛速度快、数据成本低等优点已在图像识别、故障诊断、目标检测等领域取得了一定的进展。为了提高基于深度学习的TSA 模型的自适应性,研究者们对迁移学习应用于TSA 领域进行了探索。文献［19］提出一种最小均衡样本集的生成方法。文献［20］将样本迁移、特征迁移和模型迁移应用于暂态稳定预测,提高了样本匮乏阶段模型的评估性能。文献［21］结合了样本迁移和模型迁移技术,进一步采用改进深度卷积生成对抗网络对失稳样本进行增强,使得评估结果更加可靠。文献［22］提出了一种聚类自适应主动学习（active learning,AL）的电力系统TSA 方法,降低了主动学习过程中选择样本的冗余度。

本文将深度学习、主动学习和迁移学习相结合,提出一种基于DBN 的主动迁移学习方法。离线阶段训练DBN,挖掘输入特征和暂稳评估结果之间的非线性映射关系,获得较好的TSA 效果。在线应用时,若拓扑结构和运行方式发生较大变化,首先通过短期仿真生成大量无标注样本。然后,采用结合信息熵的主动学习筛选少量最富有信息的样本进行标注,用于模型的迁移更新,显著减少了在线样本的生成时间。最后,根据源域和目标域数据分布的最大均值差异（maximum mean discrepancy,MMD）指标,选择合适有效的迁移路径,在保证模型预测精度的前提下进一步减少迁移更新的时间,缩短TSA 模型在线应用的空窗期。在3 个测试系统上验证了所提方法具有高精度、快速性和鲁棒性。

1 主动迁移学习

1.1 迁移学习和迁移路径

本文采用DBN 作为暂态稳定预测的基分类器,DBN 的原理［23］已经相当成熟,因此,不再展开叙述。采 用Adam 算 法［24］自 上 而 下 对DBN 的 权 重 和 偏 置进行微调,获得较好的暂态稳定预测效果。然而,传统人工智能模型的预测性能依赖于训练和测试样本具有相同的特征空间和相同的分布。当二者分布差异较大时,所训练模型在测试数据上表现不佳,难以进行电力系统TSA 的在线应用。迁移学习允许训练和测试数据的分布不同［25］。当处理新领域（目标域）的问题时,可以根据现有领域（源域）中训练好的模型进行快速更新。基于深度学习的TSA 在线应用和迁移学习的应用场景有很多相通之处。对于TSA 而言,离线训练好的模型应用于在线评估,等效于在源域中的原模型应用于目标域。在大部分场景下,原模型可以很好地应用于目标域。但用于模型离线训练的样本空间很难完全涵盖系统所有可能的运行工况［16］,当电力系统的拓扑结构和运行方式发生较大变化时,源域和目标域的数据分布差异较大,导致原模型应用于目标域时性能较差。此时,可结合迁移学习,在原模型的基础上更新目标域模型,使其能在新运行场景下自适应地调整参数,缩短基于深度学习的TSA 模型在线应用时的空窗期。

度量源域和目标域的数据分布差异对迁移学习至关重要［26］。本文采用MMD［27］来度量源域和目标域的数据分布差异。源域数据指的是拓扑结构和运行方式变化前系统的样本集,目标域数据指的是拓扑结构和运行方式发生较大变化后系统的样本集。MMD 的基本原理是在样本空间中找一个连续函数f,分别求出不同分布的数据集对应f的函数值均值,并将其相减,当均值差异最大时,对应的差值称作最大均值差异。MMD 的经验估计可表示为:

式中:r为高斯滤波器宽度,其决定平滑程度；a和a′为核函数的两个参数向量。

考虑不同域之间的数据分布差异,本文提出一种基于MMD 的迁移路径的选择方法,对深度学习模型的泛化能力进行量化。 如图1 所示,当IMMD＆lt;0.5 时,源域和目标域的数据分布差异较小,在线更新起点高,冻结特征提取层,仅微调最后一层输出层；当IMMD≥0.5 时,在线更新起点低,此时微调整个网络。

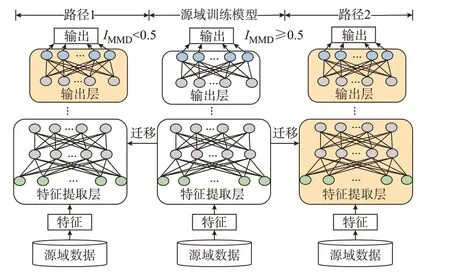
图1 考虑源域和目标域MMD 的自适应更新路径Fig.1 Adaptive update paths considering MMD of source domain and target domain

路径1:仅微调DBN 的最后一层,如图1 左半部分的阴影所示。预训练的TSA 模型的结构和参数被迁移到新模型并冻结。少量目标域的样本用来微调输出层。

路径2:微调DBN 的整个网络,如图1 右半部分的阴影所示。预训练的TSA 模型的结构和参数被迁移到新模型用来初始化新模型的参数。少量目标域的样本用来微调整个网络。

迁移学习的微调过程如下:

步骤1:提取所有隐含层的特征向量。

隐含层特征向量的提取如式（4）所示。

式中:hl为第l个隐含层的特征向量；wl为第l-1个隐含层和第l个隐含层之间的权重向量；bl为第l个隐含层的偏置向量；σ(⋅)为激活函数,本文采用sigmoid 激活函数。

步骤2:计算输出层。

DBN 输出层的计算如式（5）所示。

式 中:ŷ为DBN 输 出 层 的 预 测 向 量；wout和bout分 别为输出层的权重向量和偏置向量。

步骤3:计算损失函数值。

在第1 阶段,训练DBN 分类模型对系统的暂态稳定状态进行预测,输出包括稳定和失稳两类。此时采用交叉熵损失函数［28］,如式（6）所示。

式中:loss为损失函数值；N为训练集中样本的总数目；yk,1为第k个样本属于稳定类别的标签；yk,0为第k个 样 本 属 于 失 稳 类 别 的 标 签；ŷk,1和ŷk,0分 别 为DBN 预测第k个样本属于稳定和失稳的概率值。

第2 阶段则在第1 阶段暂态稳定状态预测的基础上,当预测结果为稳定时,进一步评估系统的稳定裕度；反之,评估系统的失稳程度,此时对应回归问题。均方根误差（root mean square error, RMSE）作为损失函数值,如式（7）所示。

式 中:IRMSE为 均 方 根 误 差 的 值；R̂k和Rk分 别 为 第k个样本稳定裕度/失稳程度的预测值和真实值。

步骤4:根据MMD 的大小选择迁移路径。

路径1 中的权重和偏置如式（8）和式（9）所示。冻结除了输出层以外的所有参数。计算损失函数值并且只微调输出层的参数wout和bout,最后得到通过路径1 优化的网络权重向量w′和偏置向量b′。

式中:frozen(⋅)为冻结参数的函数；∪表示取并集。

路径2 中的权重和偏置如式（10）和式（11）所示。计算损失函数值微调所有层的参数,最后得到通过路径2 优化的网络权重向量w′′和偏置向量b′′。

式中:initialize(⋅)为初始化参数的函数。

1.2 主动学习的样本选择

迁移学习的实施离不开目标域下的新样本,利用目标域的样本集对原模型的参数进行更新和调整。当目标域的样本过少时,在模型迁移过程中由于缺乏有效的信息,很难达到较好的评估效果。而迁移学习过程中所用的样本数量越多,在线更新越耗时。同时,采用时域仿真法对样本进行标注的过程也需要大量的时间,导致TSA 模型的在线应用存在较长的空窗期。

长期仿真的时间是整个仿真时长,根据样本的标注规则从而获得对应的标签,因此,长期仿真获得的是有标注样本；短期仿真的时间是TSA 模型的响应时间,由于暂态稳定预测的意义在于系统还未真正失稳前就能进行超前预警,TSA 模型的响应时间远小于整个仿真时长。因此,短期仿真可以在短时间内生成大量的无标注样本,然后筛选少量最富有信息的样本通过长期仿真进行标注,采用长短期仿真相结合的方式可以有效减少用于模型在线更新样本的生成时间。

在新的运行场景下,电力系统的暂态稳定边界发生偏移,预训练的TSA 模型的参数需要朝着稳定边界偏移的方向进行调整。因此,在TSA 模型的更新过程中,靠近暂态稳定边界的样本是最重要和有效的,这些样本对模型参数的调整贡献更大,称这些样本为最富有信息的样本。为了极大地减少样本的生成时间和模型的更新时间,本文提出一种结合信息熵的主动学习的样本筛选方法。采用长短期仿真相结合的方式,对少量最富有信息的样本进行标注,可以有效缩短TSA 模型在线应用的空窗期。

本文采用结合信息熵的AL 策略来进行样本选择。香农信息熵是广泛使用的信息熵［29］,将离散随机变量ξ的分布表示为式（12）。

式中:yc为第c个输出类别；pc为第c个输出类别所对应的概率值。

对于第1 阶段分类问题而言,输出类别包括稳定和失稳两类,此时ξ有两个值,分别是y1和y2；p1和p2分别为DBN 预测输出稳定类别和失稳类别的概率值。信息熵H(ξ)的计算如式（13）所示。

p1和H(ξ)之间的关系如附录A 图A1 所示。对于远离稳定边界的样本,这部分样本的稳定或失稳特征比较明显,DBN 可以准确地预测其真正的类别,因此属于确定稳定或确定失稳样本。当p1=0,p2=1（确定失稳样本）或者p1=1,p2=0（确定稳定样本）时,信息熵是最小的。而对于靠近稳定边界的样本,这部分样本往往属于临界稳定或临界失稳样本,其稳定或失稳的特征不太明显,DBN 预测其属于两个类别的概率比较接近。当p1=p2=0.5时,样本的不确定性最大,信息熵也最大。因此,信息熵可以筛选出靠近稳定边界的样本,这部分样本对暂态稳定边界的调整和模型的更新至关重要,从而保证了有效信息的识别。

对原模型的迁移更新是一个迭代过程,在新的运行场景下,通过短期仿真快速生成无标注样本集Dul。初始的关键样本集Dm为空集,源域中训练的原模型为M0,第g次迭代得到的目标域新模型为Mg。基于主动迁移学习的自适应更新过程如下:

步骤1:通过Mg-1预测Dul的分类输出概率,计算信息熵H(ξ)；

步骤2:将H(ξ)从大到小进行排列,通过长期仿真对前Nm个样本进行标注,包括分类标签（稳定/失稳）和回归标签（稳定裕度/失稳程度）；

步骤3:将Nm个样本放入数据库Dm,并从Dul中删去这些样本；

步骤4:使用Dm微调Mg-1获得新模型Mg；

步骤5:重复以上步骤,直到模型的预测准确率不再增加或者达到预设值,更新过程终止。

2 暂态稳定评估

2.1 输入特征与输出

输入特征的选择对模型的评估性能有着重要的影响,故障切除后的发电机功角轨迹簇特征具有集簇性和收敛性［30］,且维度不随系统规模的变化而变化,为本文迁移方案的实施奠定了良好的基础。因此,本文采用故障切除后发电机的功角轨迹簇特征,共包含基本特征、变化率及曲率、加速度3 大类27 个特征作为DBN 的输入。输入特征的详细描述和计算公式可参见文献［11］。

输出是和输入样本一一对应的标签集合,在本文中,首先将TSA 看成分类问题,此时输出包含稳定或失稳两类。对于预测为稳定的样本,进一步评估其稳定裕度,反之评估其失稳程度。因此,本文构造了一个先分类再回归的两阶段评估方法,使得TSA 的结果更加精细化。

对于分类预测,通过暂态稳定指数（transient stability index,TSI）决定样本的类别标签,如式（14）所示。

式中:ITSI为系统的暂态稳定指数；Δδmax为仿真时间内的最大功角差。当ITSI＆gt;0,样本是稳定的,相应的类别标签为（1,0）；否则,样本为失稳,对应的类别标签为（0,1）。

2.2 自适应评估流程

在系统的拓扑结构和运行方式发生较大变化后,若不及时更新模型,模型预测性能会持续下降。通过枚举式的时域仿真法生成新样本重新训练模型的效率和速度太低,无法满足在线时效性的要求。而主动学习和迁移学习可以在拓扑变化后仅使用轻量的计算资源就可使模型性能得以有效恢复。因此,基于大数据和深度学习的完善的TSA 包括3 个重要阶段:离线训练、模型更新和在线评估。自适应评估流程如图2 所示。

图2 电力系统暂态稳定自适应评估流程Fig.2 Adaptive assessment process for power system transient stability

1）离线训练:采用时域仿真法或者历史数据库获得用于模型离线训练的样本集；提取27 个轨迹簇特征,并采用最大最小归一化方法预处理输入特征,使得DBN 输入特征的范围在［0,1］之间；按照一定比例划分训练集和测试集。

2）模型更新:模型更新的启动方式有两种:一种是根据负荷变化规律,按照预设时间间隔进行周期性的更新；另一种是检测到系统的拓扑结构或者运行工况发生变化时,立即启动更新过程。首先,通过短期仿真生成大量的无标注样本,采用结合信息熵的主动学习筛选少量最富有信息的样本,通过长期仿真对这部分样本进行标注。然后,计算源域和目标域的数据分布差异MMD 值,选择合适的迁移路径。最后,通过自适应迭代更新过程得到适用于当前工况的新模型。

3）在线评估:通过相量测量单元（phasor measurement unit,PMU）获得广域量测数据,采用基于可信度的分层实时预测方法［12］,进行动态实时的电力系统TSA。

2.3 模型的评估指标

2.3.1 分类模型的评估指标

TSA 是一个典型的非平衡分类问题［31］,评估结果如表1 所示。其中,Ts和Tus分别为稳定样本和失稳样本正确预测的数目；Fus为稳定样本误判为失稳样本的数目；Fs为失稳样本漏判为稳定样本的数目。

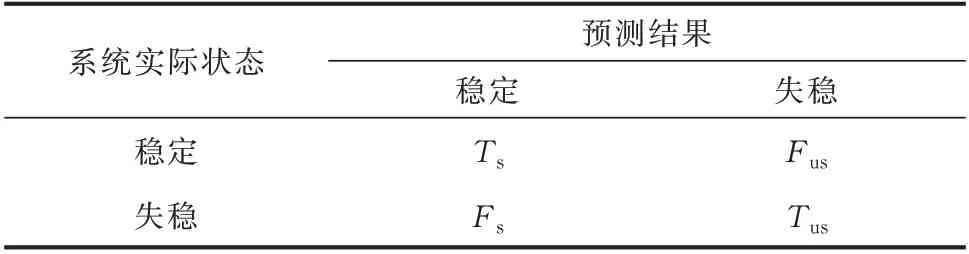
表1 暂态稳定评估的结果Table 1 Result of transient stability assessment

本 文 采 用 的 评 估 指 标 包 括Acc、Tsr、Tur和Gmean。Acc为整体的预测准确率,Tsr为稳定样本的识别率,Tur为失稳样本的识别率,Gmean为一个综合指标。其计算方法如式（15）至式（18）所示。

2.3.2 回归模型的预测目标

当预测结果为稳定时,评估系统的稳定裕度有利于实施后续的预防控制措施；当预测结果为失稳时,评估系统的失稳程度有利于快速采取相应的紧急控制措施。因此,评估系统的稳定裕度或失稳程度指标对调度人员有一定的参考意义。本文仿照文献［32-33］构造稳定裕度和失稳程度指标。

稳定裕度Bs的计算过程如下:

式中:ts为仿真时间,本文中ts为5 s；δv为第v台发电机的功角；S为转子角包络线积分的受扰程度,将其归一化后得到稳定裕度指标Bs；Smax和Smin分别为所有稳定样本集中受扰程度S的最大值和最小值。

失稳程度Bus的计算过程如下:

式中:tcl为故障清除时刻；tus为系统失稳的时刻；T为从故障清除到系统失稳所经历的时间；Tmax和Tmin分别为所有失稳样本集中T的最大值和最小值。T越大,意味着故障清除后有越多的时间来采取紧急控制,因此失稳程度Bus越小；反之,Bus越大。

3 算例分析

算例系统采用IEEE 10 机39 节点系统、NPCC 48 机140 节点系统和华中电网。电力系统仿真软件采用Power System Tool （PST） 3.0［34］和电力系统分析综合程序（power system analysis software package, PSASP）。深度学习框架为TensorFlow,编程语言为Python。

3.1 IEEE 39 节点系统

负荷水平考虑从75%～120%,以5%为变化步长,并相应地调整发电机的出力保证潮流计算收敛；故障持续时间为1 周期到11 周期,以1 周期为变化步长；故障线路为34 条不含变压器的输电线路；故障位于每条线路的0%～90%处,以10%为变化步长；故障类型设置为三相短路故障。共生成37 400个有效样本,其中,稳定样本数为22 712,失稳样本数为14 688,按照4︰1 的比例随机划分训练集和测试集。

3.1.1 DBN 模型评估性能测试与分析

为了验证DBN 用于TSA 时的性能,将DBN 模型的预测结果和多层感知机（multilayer perceptron,MLP）以及SVM、DT、RF 和KNN 进行对比。DBN输入层的神经元个数为27,采用逐层搜索隐含层节点数,层数依次叠加的实验方式确定DBN 的结构参数,最终得到最佳结构为［27, 200, 100, 50, 30,2］,批大小为187,自适应学习率为0.001。MLP 的结构参数与DBN 相同。SVM 的核函数采用径向基核函数。DT 采用C5.0 算法,KNN 中最近邻个数取为18。DBN 和各模型分类预测的结果如表2 所示,考虑到随机性,所有实验重复10 次,取其平均值作为最终的评估结果。

表2 不同分类模型的性能比较Table 2 Performance comparison of different classification models

测试结果表明,相比其他预测模型,DBN 在Acc和Gmean指标上有着更加明显的优势,所有预测指标均保持在98.9%以上。DBN 的预测准确率Acc比MLP 高2.66%,Gmean值 高3.52%。虽 然MLP 和DBN 采用了相同的结构和参数,但其仅采用了反向传播算法进行监督训练,参数难以得到有效优化,因此Gmean值最低。RF 基于多个DT 进行决策,预测性能优于DT,但其评估指标依然低于DBN,预测准确率Acc比DBN 低1.81%,Gmean值低1.42%。因此,DBN 可以充分发挥深层架构的特征提取能力,采用两阶段的训练方法使得参数得以有效的优化。

DBN 对稳定样本的识别率Tsr为98.93%,即对稳定样本的误判率为1.07%；对失稳样本的识别率Tur为98.90%,即对失稳样本的漏判率为1.10%。相比其他预测模型,DBN 对稳定样本的误判率以及对失稳样本的漏判率都较低,说明深层架构可以有效地挖掘输入特征和输出结果之间的非线性映射关系,在TSA 中表现出优越的预测性能。同时,通过测试可以发现,少量的误判和漏判样本往往是处于稳定边界的样本,这类型样本的稳定或失稳特征不够明显,在线应用中采用基于可信度的分层实时预测方法［12］,等到下一时间层得到更多的信息后方可进行准确预测。值得说明的是,本文仅以DBN 为研究载体,所提方法仍然适用于CNN、LSTM 等深度学习模型。

表3 展示了各模型对稳定裕度Bs和失稳程度Bus的回归预测结果,DBN 可以准确地拟合系统的稳定裕度和失稳程度,其预测均方根误差IRMSE显著低于其他模型,进一步验证了DBN 在TSA 中优越的评估性能。

表3 不同回归模型的性能比较Table 3 Performance comparison of different regression models

3.1.2 未训练的超负荷场景下的迁移

为了模拟在线应用时不在调度人员预知范围内的运行条件的变化,验证本文所提主动迁移学习方法的有效性,将负荷水平分别增加至135%,140%,145%和150%的基准负荷,同时调整发电机的出力保证潮流计算收敛,故障线路、故障位置、故障清除时间和故障类型与IEEE 39 节点系统初始故障集设置相同。共仿真生成14 960 个样本,包括3 183 个稳定样本和11 777 个失稳样本,将过负荷样本集按1︰1 划分训练集和测试集。3.1.1 节离线训练的原模型在过负荷场景下的测试结果如表4 所示。

表4 原模型在过负荷场景下的测试结果Table 4 Testing results of original model in overload scenarios

由测试结果可知,在过负荷场景下,离线训练的原模型性能急剧下降,Tsr指标低于75%,无法进行在线应用。因此,离线场景（源域）下训练的原模型需要迁移更新至新的过负荷场景。共有4 种不同的路径用来更新原DBN 模型,路径1 和路径2 是在1.1 节详细介绍的本文所采用的两种迁移路径。

路径3 的迁移方法是将原模型的结构迁移至新模型,随机初始化DBN 的参数。使用主动学习所筛选的高信息熵的样本重新训练DBN 模型。

路径4 的迁移方法是将原模型的结构迁移至新模型,随机初始化DBN 的参数。使用随机选择的训练样本重新训练DBN 模型。

按照4 种路径,分别从训练集中筛选187,374,561,…,7 293,7 480 个样本对原模型进行迁移更新。其中,利用主动学习每次筛选的高信息熵的样本数量为187,即Nm=187。迁移过程中DBN 的训练参数为:初始学习率为0.001,批量大小为187。采用不同路径下DBN 的迁移更新效果如图3所示。

图3 不同迁移路径下的评估指标对比Fig.3 Assessment index comparison for different transfer paths

由测试结果可知,路径2 的Acc和Tsr指标优于其他3 种路径。对比路径1 和路径2,过负荷场景下的IMMD＆gt;0.5,仅微调输出层没有给目标域的新样本留出充足的学习空间,因此评估性能较差。本文中阈值0.5 的选择是多次试验的结果。通过设置不同的拓扑结构和运行条件来采集多个不同分布的目标域数据。不同迁移路径下的预测准确率Acc随IMMD的变化曲线如附录A 图A2 所示。对比路径2 和路径3,采用迁移的方式共享原模型的结构和参数给新模型提供了一个较好的初始值,有助于一个良好的学习起点,模型预测性能优于重新训练。对比路径3 和路径4 可知,主动学习可以筛选出少量最富有信息的样本,有利于调整TSA 的分类边界,提高原模型的预测性能。路径2 仅使用1 683 个样本即可将Acc指标恢复到97.5%以上,因此,只有1 683 个样本需要通过长期仿真进行标注。而当路径3 和路径4 所使用的样本数量达到7 000 以上时,预测准确率Acc仍然没有达到97.5%。因此,本文所提方法不仅可以有效地恢复模型的评估性能,而且可以进一步减少在线样本生成时间和模型的更新时间,实现了在线快速连续的自适应TSA。

为了进一步分析采用主动学习筛选高信息熵样本的有效性,采用t 随机近邻嵌入（t-distributed stochastic neighbor embedding, t-SNE）［35］将 路 径2（主动学习筛选高信息熵样本）和路径4（随机选择样本）所选取的前935 个样本的输入特征进行降维可视化,结果如图4 所示。

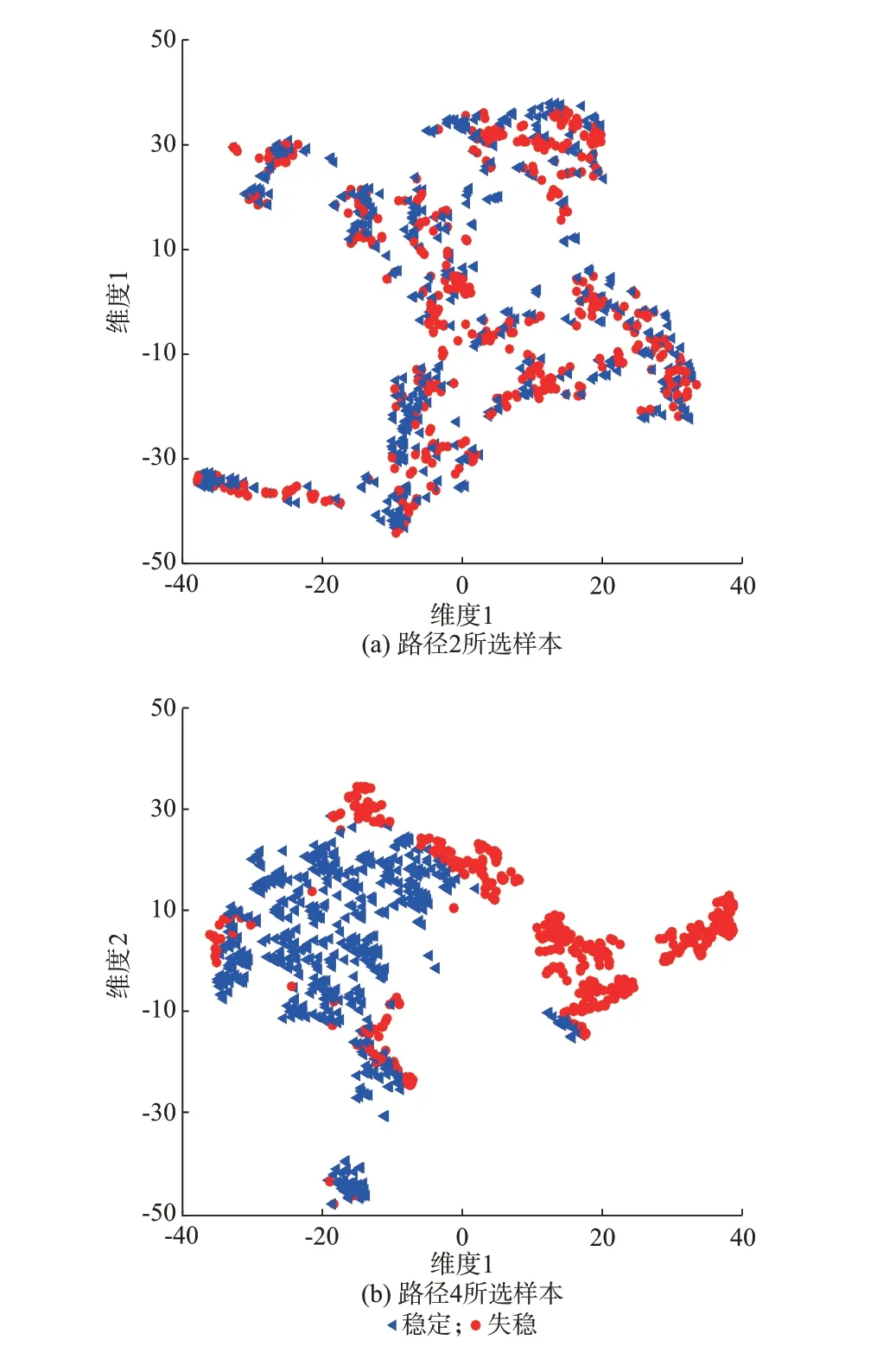
图4 路径2 和路径4 所选择样本的可视化结果Fig.4 Visualization results of samples selected by path 2 and path 4

重叠区域的样本是靠近稳定边界的样本,也是暂态稳定预测误判和漏判的主要原因,这些样本对新分类器的获得至关重要。比较路径2 和路径4,路径2 可以筛选出目标域下更多重叠区域的样本,保证了目标信息的含量最大,验证了本文结合信息熵的主动学习筛选少量最富有信息样本的有效性。

3.1.3 未预料的拓扑结构改变的迁移

为了模拟在线应用时无法事先预料的拓扑结构的变化,本文仿照文献［19］的系统拓扑结构图和运行方式新增如下4 种场景。

场景A:负荷水平调整为50% 的基准负荷水平,退出运行1 台发电机和4 条线路。共仿真生成6 900 个样本,其中,稳定样本5 768 个,失稳样本1 132 个。随机划分3 900 个作为训练集,其余作为测试集。

场景B:负荷水平调整为50% 的基准负荷水平,退出运行5 台发电机和8 条线路。共仿真生成了6 900 个样本,其中,稳定样本4 207 个,失稳样本2 693 个。随机划分3 900 个为训练集,其余作为测试集。

场景C:负荷水平调整为150%的基准负荷水平,投入运行2 台发电机和4 条线路。共仿真生成了3 960 个样本,其中,稳定样本1 775 个,失稳样本2 185 个。随机划分2 960 个为训练集,其余作为测试集。

场景D:负荷水平调整为150%的基准负荷水平,投入运行5 台发电机和10 条线路。共仿真生成了8 580 个样本,其中,稳定样本3 419 个,失稳样本5 161 个。随机划分4 580 个为训练集,其余作为测试集。

4 种场景下不同路径的迁移更新效果见附录B表B1—表B4。由测试结果可知,当系统的拓扑结构和运行方式发生较大变化时,离线训练的模型性能劣化。根据MMD 指标,可以选择最优的迁移路径。对于场景A 和场景B,IMMD＆lt;0.5,选择路径1 局部微调输出层,可以有效地恢复和提高DBN 模型的预测性能。虽然其评估指标略优于路径2,但是路径1 可以进一步缩短更新时间。对于场景C 和场景D,IMMD＆gt;0.5,此时路径1 无法满足在线应用时的性能要求,选择路径2 进行更深层次的微调,也从侧面验证了本文阈值选择0.5 的合理性。根据MMD指标,可以有效度量不同场景下的数据分布差异,从而可以快速有效地选择最合适的迁移路径,有利于提高模型的预测性能和更新效率。

3.2 NPCC 48 机140 节 点 系 统

NPCC 48 机140 节点系统中包含48 台发电机、233 条线路和140 条母线。负荷水平为75%～120%的基准负荷,以5%为变化步长；故障线路为不含变压器的传输线路；故障清除时间考虑故障后5 个周期清除近端故障,6 个周期清除远端故障或者9 个周期清除近端故障,10 个周期清除远端故障。共生成25 045 个样本,包括21 029 个稳定样本和4 016 个失稳样本。随机划分15 045 个样本作为训练集,剩余10 000 个样本作为测试集。

3.2.1 分类模型迁移效果分析

对于一个新拓扑结构的电力系统,传统方法往往是重新仿真生成大量的有标注样本,并且重新训练一个新模型,这一过程通常需要花费大量的时间。在本节中,IEEE 39 节点系统作为源域,NPCC 140 节点系统作为目标域。IMMD为0.528,因此选择路径2 迁移更新原模型。无标注样本的数量为15 045,结合信息熵的主动学习所筛选的样本数为748。迁移更新后的DBN 记作 TL-DBN,原模型、TL-DBN 和重新训练的模型预测性能如表5 所示。所提方法和重新训练各阶段的耗时对比如表6所示。

表5 NPCC 48 机140 节点系统采用不同模型的性能对比Table 5 Performance comparison of NPCC 48-unit 140-bus system using different models

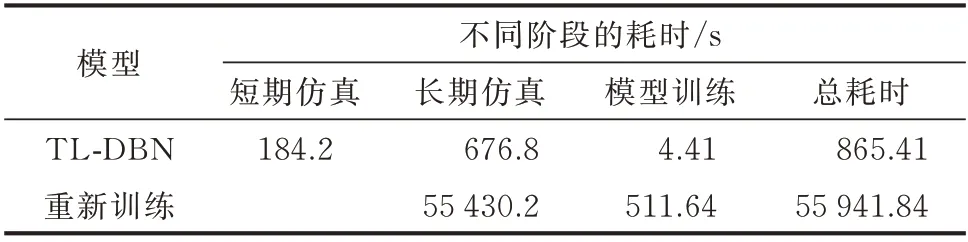
表6 NPCC 48 机140 节点系统不同模型耗时对比Table 6 Time consumption comparison of NPCC 48-unit 140-bus system using different models

测试结果可知,所提的主动迁移学习方法的预测性能要优于重新训练。当源域系统中预训练的模型直接应用于NPCC 48 机140 节点系统时,预测准确率Acc仅有80.28%,综合指标Gmean为81.53%。通过自适应的主动迁移学习路径更新微调后,预测准确率Acc恢复至97.10%,Gmean值恢复至96.89%。所提主动迁移学习方法的更新时间为4.41 s,而重新训练的时间为511.64 s,模型的更新效率提高了116 倍。此外,所提方法采用长短期仿真相结合方式,大幅减少了在线样本的生成时间。短期仿真生成无标注样本的耗时是184.2 s,主动学习筛选高信息熵样本的时间为0.1 ms,可以忽略不计；长期仿真对少量最富有信息的样本标注时间是676.8 s。因此,本文所提方法的总耗时在15 min 内,能够满足时效性的需求。相比于重新训练,主动学习和迁移学习相结合的方法可以同时减少样本生成时间和模型更新时间,极大缩短了在线应用的空窗期,对TSA 模型的在线应用具有重要意义。

3.2.2 回归模型迁移效果分析

在第1 阶段分类预测的基础上,进一步评估系统的稳定裕度和失稳程度。将IEEE 39 节点系统预训练的稳定裕度和失稳程度回归模型迁移至NPCC 48 机140 节点系统。为了直观地展示回归模型预测的结果,随机选择100 个样本,迁移前和迁移后回归模型预测的结果如图5 所示。

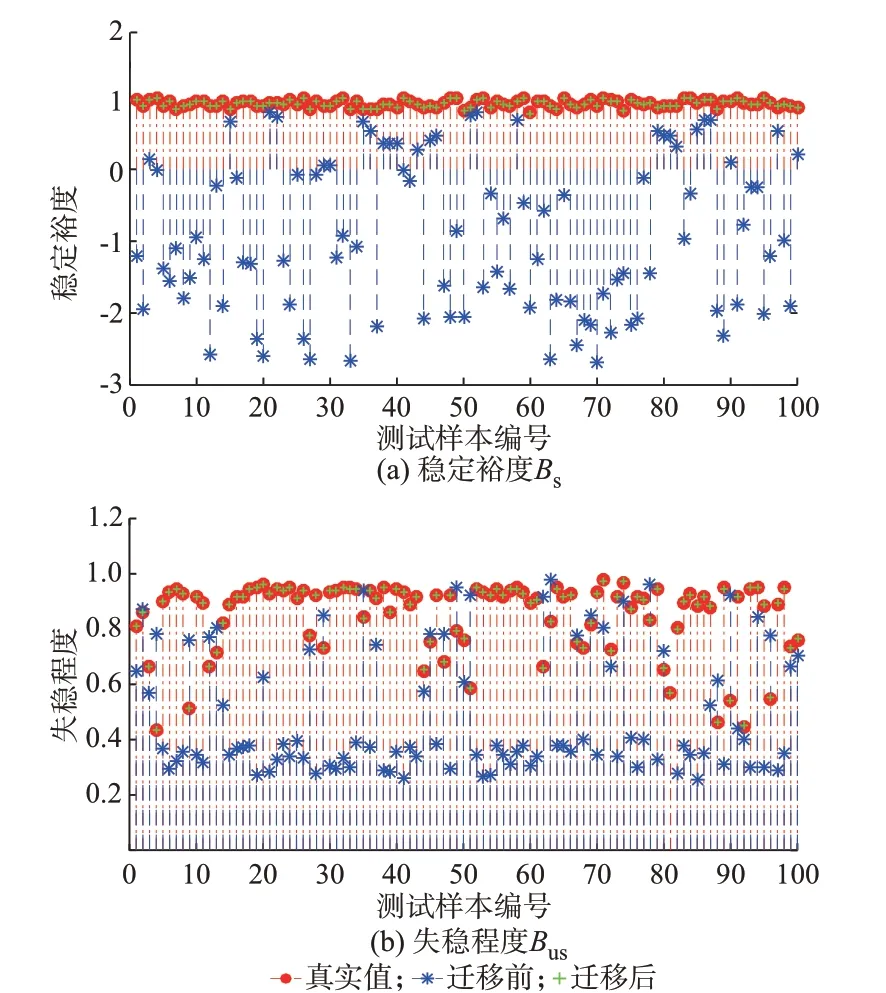
图5 回归模型的迁移效果Fig.5 Transfer effect of regression models

由图5（a）可知,IEEE 39 节点系统预训练的稳定裕度回归模型在NPCC 48 机140 节点系统中完全失效,计算预测均方根误差IRMSE达到2.219。迁移前的稳定裕度预测值出现了负值,与实际状况不一致。迁移之后的IRMSE为0.087 8,可以拟合真实的稳定裕度值,模型的迁移更新时间为8.74 s。对于失稳程度回归模型,虽然预测值没有出现负值,但其和真实值之间仍然存在较大的偏差。通过所提的主动迁移学习方法,可以将失稳程度回归预测的IRMSE从0.456 减小到0.11。迁移更新后的回归模型可以很好地拟合系统的失稳程度,对调度人员下一步决策有一定的参考价值。因此,本文所提方法不仅适用于稳定与否预测的分类模型,也适用于稳定裕度和失稳程度评估的回归模型。

3.3 华中电网

华 中 电 网［36］含 有690 台 发 电 机、6 022 台 变 压器、4 474 条线路和8 492 条母线。负荷水平考虑75%～120%的基准负荷水平,以5%为变化步长,发电机出力随负荷相应调整；分别选取“江西—安关Ⅰ线”“江西—安跑Ⅱ线”“华中—乐鹰Ⅰ回线”和“湖北—泉径Ⅰ回线”为故障线路；故障位置考虑10%～90%处,以10%为变化步长；故障类型包括单相短路故障、两相短路故障以及三相短路故障。共生成14 040 个样本,包括稳定样本10 446 个、失稳样本3 594 个,按照2︰1 的比例随机划分训练集和测试集。

3.3.1 迁移效果分析

将IEEE 39 节点系统离线训练的模型作为原模型,测试数据采用华中电网的测试集,实验结果如表7 所示,原模型在目标域的预测性能较差,Gmean值仅为72.07%。根据MMD 指标选择路径2 微调整个网络,无标注样本的数量为9 360,结合信息熵的主动学习所筛选的样本数为1 870,模型更新耗时11.5 s 即可将预测准确率Acc恢复到98.48%,综合指标Gmean恢复到97.64%,相比于重新训练的时间140.36 s,模型更新效率提高了12.2 倍。采用本文方法主动学习所筛选的高信息熵的样本数为1 870 个,因此,仅需要对这1 870 个样本通过长期仿真进行标注,而重新训练需要的有标注样本是9 360 个,样本生成时间大幅减少。

表7 华中电网采用不同模型的性能对比Table 7 Performance comparison of central China power grid using different models

稳定裕度和失稳程度回归模型的迁移更新效果如表8 所示。稳定裕度Bs回归预测的均方根误差IRMSE从2.518 减小到0.089,失稳程度Bus回归预测的均方根误差IRMSE从0.732 减小到0.095,迁移更新后的回归模型可以准确地拟合系统的稳定裕度和失稳程度。本文所提方法不仅可以自适应地追踪系统的拓扑结构和运行方式的变化,也可以在结构和规模完全不同的系统间进行迁移,具有一定的鲁棒性。

表8 华中电网迁移前后回归模型性能Table 8 Performance of regression models before and after transfer for central China power grid

3.3.2 实际故障数据验证

2021 年11 月7 日05:26,河南多地受强风、冰雹等恶劣天气影响,短路故障导致天中直流换相失败,500 kV 香武线、姚涂线、汉郑线3 条线路相继跳闸共6 次,根据PMU 的实时量测数据,包含05:26:30—05:27:30 共1 min 的数据,PMU 的数据采样间隔为20 ms,共3 000 个时刻的采样点,读取PMU 信息中的功角电气量,提取轨迹簇特征,利用更新好的DBN 模型,采用基于可信度和滑动时间窗口的形式［12］进行动态实时预测。评估结果如附录B 表B5所示,其中,稳定裕度评估结果表示在采样时刻内稳定裕度的最小值。在保护装置正确动作的情况下,采用更新好的DBN 模型的预测结果和实际状况一致,验证了所提方法在线应用的有效性。

4 结语

针对电力系统暂态稳定评估模型的自适应性问题,本文提出一种结合信息熵的主动迁移学习方法,在3 个算例系统上进行测试和验证,结论如下:

1）根据源域和目标域的数据分布差异,可以灵活选择最合适的迁移路径,提高了暂态稳定评估模型的自适应性,进一步减少了模型的更新时间,有效缩短了在线应用的空窗期。此外,所提方法可以在结构和规模不同的系统间进行迁移,具有一定的鲁棒性。

2）结合信息熵的主动学习可以在短时间内筛选出少量最富有信息的样本,采用长期仿真对高信息熵的样本进行标注,不用标注所有的样本,显著减少了在线样本的生成时间。

本文所提暂态稳定自适应评估方法对迁移路径的选择依赖于最大均值差异这一指标,在后续工作中,将继续深入研究最大均值差异的区间划分和阈值选择方法。此外,用于暂态稳定评估的离线样本集大多是通过时域仿真法生成,未来将在样本层面进行研究,使仿真样本更加接近实际的量测数据,使得自适应评估模型更加完善。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。