基于信息物理融合的微能源网统一调控架构及优化运行

杨 义，杨 苹，2，李壮壮，唐玉烽，陆冠鹏

（1.华南理工大学电力学院,广东省广州市 510630；2.广东省绿色能源技术重点实验室（华南理工大学）,广东省广州市 510630）

0 引言

目前,全球化石能源日渐枯竭,环境污染日趋严重,能源结构亟待转型升级。微能源网（microenergy grid,MEG）通过能源的梯级利用和多能互补可以有效提高能源的综合利用效率、减少环境污染,是未来新型电力系统的重要组成部分［1］。MEG 的优化运行一直是国内外研究的热点［2-3］,而建模是MEG 进行优化分析的理论基础。

关于MEG 的优化调控建模主要从整体的角度和从局部的角度开展。从整体的角度对MEG 进行建模的方法不关注组成MEG 系统的各能源单元的建模。典型代表是文献［4-6］提出的能源集线器建模方法。从局部的角度对MEG 进行建模的方法主要 关 注MEG 内 部 组 成 结 构［7-8］、各 能 源 单 元 的 建模［9］。然而,上述2 类建模方法主要从MEG 系统的输入-输出关系进行描述,并未考虑MEG 内各能源单元的运行状态,难以清晰描述MEG 中各能源单元的状态转移过程。此外,现有的MEG 模型大多仅考虑物理系统,缺乏对信息部分的特性描述。从信息和物理2 个层面全面描述系统的特性,分析信息流和能量流的交互机制,能施以更为精确而灵活的调控,可以提高系统优化调控的灵活性、有效性和精准性,同时能够降低系统的运行成本。信息物理系统（cyber-physical system,CPS）理论的提出为实现MEG 系统信息流和能量流的描述提供了技术手段［10］。

近年来,CPS 理论在电力系统中开始得到广泛研究［11-12］,文献［13］分析了信息物理融合的电网层次结构,采用关联矩阵描述电力信息系统、物理系统以及二者间的耦合关系。文献［14］建立了电网信息物理系统信息流-能量流混成计算模型,并基于节点-支路关联矩阵建立了电网静态模型,较为全面地描述了电网中信息流和能量流的耦合关系。文献［15］基于关联矩阵建立了表征电网CPS 中信息层和物理层的耦合关系模型,并定量分析了信息故障对电网CPS 可靠性方面的影响。文献［16］提出了一种集中式控制的微电网CPS 分层建模方法,实现了微电网中各单元运行状态轨迹的可观测。文献［17］提出了一种分布式控制的微电网信息物理融合建模方法,实现了微电网CPS 运行的可靠性评估。以上文献大多应用CPS 理论对系统进行建模,研究能量流和信息流间的耦合关系,而MEG 作为CPS应用的重要领域,尚缺乏一个统一的架构和模型。此外,现有的模型对于资金流的考量较少,缺乏对能量流、信息流和资金流三者之间关系的描述与分析。

为此,本文从CPS 的视角出发,构建了一种新型的MEG 统一调控架构,对MEG 内能源单元的运行状态及运行状态转换的各个阶段下能量流、信息流和资金流的关系进行描述,实现MEG 在优化过程中各能源单元状态转移轨迹的精准调控。

1 MEG 的典型结构

本文所研究的MEG 典型结构由能源生产单元、能源转换单元、能源储存单元以及能源消费单元组成,具体如附录A 图A1 所示。

能源生产单元包括光伏、风电等可再生能源以及电网和天然气网。能源转换单元主要实现不同形式能源间的相互转化,具体包括燃气轮机（gas turbine,GT）、燃气锅炉（gas boiler,GB）、余热锅炉（waste heat boiler,HB）、电制冷机（electric chiller,EC）以及吸收式制冷机（absorption chiller,AC）,例如EC 将电能转换成冷能,AC 通过吸收热量将热能转换成冷能。能源储存单元包括电池储能（battery storage,BS）装置、储热（thermal storage,TS）装置和储冷（cold storage,CS）装置。在能量有富余时实现能量的储存,能量不足时进行能量释放。能源消费单元包括电负荷、热负荷和冷负荷。

2 基于CPS 的MEG 统一调控架构

本章对MEG 中的能量流、信息流和资金流的互动关系进行精准描述,建立基于CPS 的MEG 调控模型框架。

2.1 MEG 统一调控架构

本节采用分层描述方法,将MEG 统一调控模型分为对象层、融合层和优化层,其框架如图1 所示。不同层级内部功能相对独立,各层级之间通过信息流交互。

图1 MEG 统一调控模型框架Fig.1 Unified dispatch and control model framework of MEG

1）对象层:由传感器、执行器以及各种能源单元等物理设备构成。传感器负责将感知到的能源单元状态信息上传给融合层；执行器接收优化层下达的控制指令,用于调整和控制物理设备的运行；能源单元用于实现能量的转换、储存和分配等。

2）融合层:该层级作为对象层和优化层的中间部分,一方面,对对象层上传上来的各能源单元运行状态信息进行分析和处理,并基于状态机对能源单元的运行状态转移过程以及驱动状态转移的条件进行描述,构建能源单元的状态转移轨迹,为优化层做出决策提供参考；另一方面,基于状态机对MEG 中的能量流、信息流和资金流三者间的交互影响进行描述。

3）优化层:完成系统的全局优化管理决策。该层级将MEG 系统中各单元的运行状态和运行约束考虑在内,基于融合层中能源单元的状态转移轨迹,制定系统的全局最优运行策略,以最优的结果驱动对象层中的能源单元运行。

2.2 层间交互描述

对象层、融合层和优化层3 层之间通过数据的自动流动实现交互,由状态感知、分析、决策和执行4 个环节闭环构成,如附录A 图A2 所示。

状态感知:状态感知由对象层执行,对象层通过传感器、物联网等数据采集设备采集各能源单元的运行状态数据,完成能量流到信息流的转换过程。

分析:分析是对数据的进一步处理,由融合层执行。融合层通过数据挖掘、机器学习等数据处理分析技术对数据进一步分析和处理,转换为决策层做出决策所需要的状态数据,为决策提供参考。

决策:决策是对信息的综合处理,由优化层执行。优化层权衡判断当前时刻所获取的来自融合层提供的所有信息,在一定的约束条件下,为实现某个优化目标做出最优决定,并形成最优决策对对象层中的能源单元进行控制。

执行:执行是对决策的精准执行,由对象层执行。将决策层产生的决策指令转换成能源单元可以执行的命令函数,将转化结果转换成能源单元下一个运行状态的函数,即信息流到能量流的转换过程。

上述闭环过程保证了MEG 能够朝着更优化的方向发展,实现了微能源系统运行状态的更新。

3 基于CPS 的MEG 分层建模

本章基于所提出的MEG 统一调控架构,根据不同层级的各自特点和功能,采用不同的建模方法,建立了各层级的模型。3 层模型的组合形成了信息物理融合的MEG 整体模型。

3.1 对象层

对象层采用特征向量的形式统一描述能量流、信息流和资金流的特征。

1）能量流特征描述

在能源的生产、传输、分配以及消费等环节中,能量流会在各能源单元之间流动,且具有方向性,可以用如下表达式进行描述:

式中:E(∙)为描述能量流的特征向量；α为输入的能源类型,可以为电、热、气等能源；Pin为能源的输入功率；β为输出能源类型,可以为电、热、气、冷等能源；Pout为能源的输出功率；SE为能量流的运行状态；ΔTE为能源的控制周期。

能量流示意图如图2 所示。

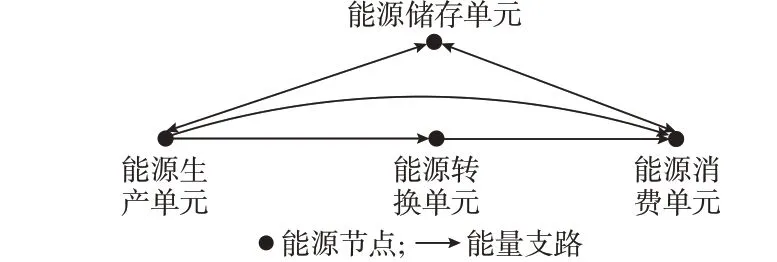
图2 能量流示意图Fig.2 Schematic diagram of energy flow

2）信息流特征描述

信息流用于描述信息的采集、传输、处理、分析和控制等环节,可以用下式进行描述。

式中:I(∙)为描述信息流的特征向量；Ri,t为t时段能源单元i的采集虚拟信号；Yi为t时段能源单元i用于分析计算的中间变量；Ui,t为t时段能源单元i的输出控制信号；SI为信息流的运行状态；Δtc为信息网络通信时延；Δtb为信息网络计算时延。

信息流示意图如图3 所示。

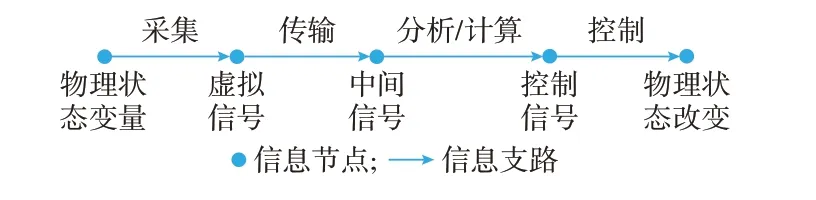
图3 信息流示意图Fig.3 Schematic diagram of information flow

3）资金流特征描述

在能源的生产和消费等过程中会产生成本和收益,表现在资金流会在不同的能源主体间流动,可以如式（3）所示描述资金流。

式中:C(∙)为描述资金流的特征向量；cr为能源主体在能源的生产和消费过程中产生的成本；cb为能源主体在能源的生产和消费过程中产生的收益。资金流示意图如附录A 图A3 所示。

3.2 融合层

融合层基于状态机对能源单元的运行状态转移过程进行建模,并对MEG 中的能量流、信息流和资金流三者间的交互影响进行描述。其中,能源单元运行状态转移建模见附录B。

能源单元状态转移模型中,状态之间转移的概率可以通过能源单元大量的历史运行统计数据或者观测数据得到,其计算方法见文献［18］。状态之间转移概率的计算通常用于设备或者系统的可靠性分析方面。由于本文不涉及可靠性分析,不考虑状态之间的转移概率。本文更多关注的是状态之间的转移条件,只要状态转移条件满足,就会触发相对应状态间的转移。

采用状态机对MEG 中的能量流、信息流和资金流间的相互关系进行描述。建立融合层的模型如图4 所 示。图 中:S1至S4为 状 态；GEI为 能 量 流 影 响信息流运行状态的条件集合；GIE为信息流影响能量流运行状态的条件集合；GEC为能量流影响资金流运行状态的条件集合；GCE为资金流影响能量流运行状态的条件集合；GCI为资金流影响信息流运行状态的条件集合；GIC为信息流影响资金流运行状态的条件集合。

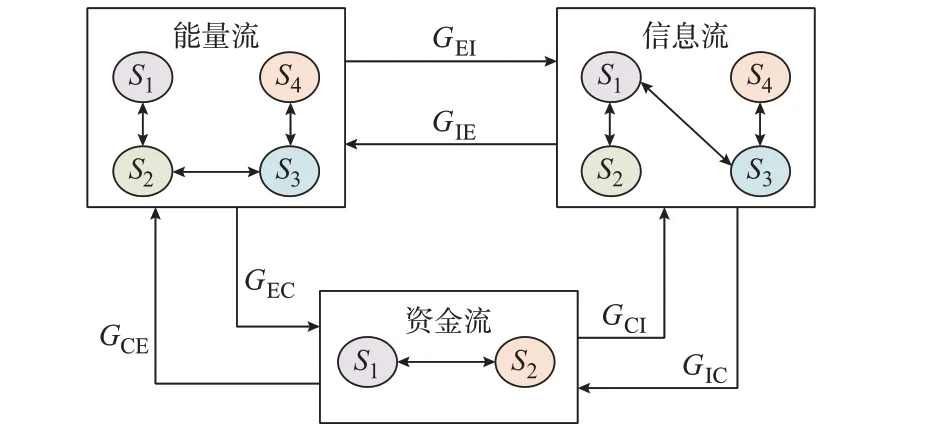
图4 基于状态机的融合层模型Fig.4 Model of fusion layer based on state machine

图4 中的每个方框分别表示能源单元（能量流）、信息单元（信息流）和资金流的状态,方框里面的圆圈表示各自存在的运行状态,圆圈之间的箭头表示不同状态之间的转移过程,例如能源单元会存在启动、正常运行、故障等状态,并在运行过程中会在上述状态间进行转移。信息单元会存在数据采集超时、采集故障、传输延时以及数据丢包等状态。资金流则会存在成本和收益2 种状态。箭头上标注的G是一个描述MEG 中能量流、信息流和资金流状态转移条件的集合,如式（4）所示。

式中:E、I和C分别为能量流、信息流和资金流的状态转移条件。

图4 中,方框之间的边表示能量流、信息流和资金流三者之间的交互关系。信息物理融合的MEG内部能量流、信息流和资金流交互影响,具体表现为:1）不同时段不同的价格信号会影响各能源单元的输出功率,即资金流影响能量流,不同能源单元的出力情况直接导致其运行成本的变化,从而影响系统及其他能源单元的资金利用状态,即能量流影响资金流；2）能源单元输出功率的变化直接影响信息系统采集到的状态数据,即能量流影响信息流,而信息系统下发的控制指令会影响能源单元的运行状态,即信息流影响能量流；3）价格信号的变化通过通信网络直接影响信息系统接收到的相关价格输入变量,即资金流影响信息流,而信息系统传输数据的丢失又会影响价格的获取,即信息流影响资金流。由此可得出,能量流与资金流互为驱动,信息流为二者的支撑。

本节所建立的状态转移模型是优化层进行优化调控的基础,状态转移模型的作用在于可以设计和选择系统的最优状态转移轨迹,如MEG 在完成某一目标时,需要从状态S1转移到状态S8运行。假设从状态S1转移到状态S8共可形成m条状态转移路径,如图5 所示。

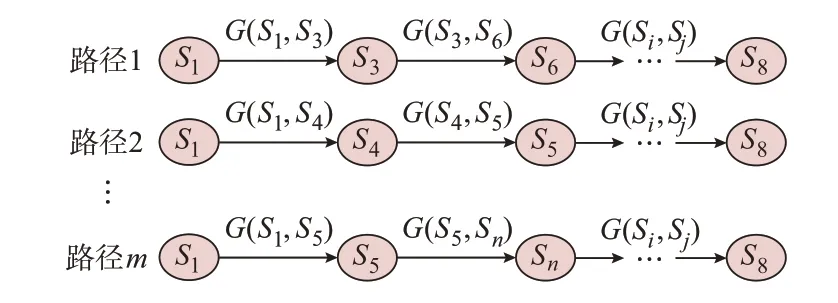
图5 状态转移路径示意图Fig.5 Schematic diagram of state transition path

MEG 根据优化层确定的优化目标和图5 所示的MEG 状态转移模型,以某一指标为依据来设计和选择一条系统的最优状态转移轨迹,这里选择最优轨迹的依据指标可以是系统的经济性指标（例如,运行成本最小）,也可以是系统的稳定性等指标。

状态转移模型给出了能源单元在不同状态间的转移条件,为优化层确定MEG 的优化运行策略提供m条可转移的路径。因此,当以MEG 运行成本最小为目标时,MEG 中的优化层可根据当前可控能源单元的运行状态以及不同状态间的转移条件,通过分析MEG 内部能量流、信息流和资金流的状态和流向,基于每小时电价的引导,优化配置MEG 内各单元的运行状态,并整合MEG 中各类可调节资源进行统一优化调控,实现MEG 的经济运行。

3.3 优化层

优化层基于融合层模型提取优化变量,建立MEG 优化调控的目标函数,将MEG 系统中各能源单元的运行状态和运行约束考虑在内,求解MEG的优化调控模型,以最优的结果调控对象层中可控单元。本文以MEG 日运行成本最低为目标,建立优化层的模型,如式（5）所示。

式中:Cr为MEG 日运行总成本；ceb,t和PGridb,t分别为t时段购电电价和向电网购入的电功率；ces,t和PGrids,t分别为t时段售电电价和向电网出售的电功率；cpg,t为t时段的天然气价格；PGT,t和HGB,t分别为t时段GT 的发电功率和GB 的产热量；ηgt和ηgb分别为GT和GB 的转换效率；Δt为调控时长；T为调控周期,本文取24；Y（X,S）为MEG 系统中各能源单元的状态更新函数,其中,X为优化变量,S为能源单元运行状态变量；Z（X,S）为MEG 系统及各能源单元运行的约束条件,这里的约束条件包括MEG 的能量平衡约束、能源单元的出力约束、能源转换单元的运行约束、能源储存单元的运行约束、向电网购售电约束、向天然气网购气约束等［8］。

上述建立的目标函数式（5）加上约束条件构成了一个典型的0-1 混合整数非线性规划（mixedinteger nonlinear programming,MINLP）问题,将本文的优化问题写成MINLP 典型形式,如式（6）所示。

式中:Z(∙)为目标函数；x为变量矩阵；xc为连续变量矩阵；xl为整数变量矩阵；A、Ac,n、Al,n、Bn为系数矩阵,其中,n为约束条件的数量。

针对MINLP 问题的求解有很多算法,本文选择分枝-割平面法对其进行求解［19］。该方法对所提模型进行初始线性规划（linear programming,LP）松弛。LP 松弛问题是指将原问题中的整数变量松弛为连续变量（例如将0-1 变量u松弛为0 ≤u≤1）,松弛后对其的可行解空间反复地分割为子空间（称为分枝）,对每个子空间内搜寻最优解,并且在分枝结束后更新上下界。通过排除不满足已知可行解集上下界的子空间,不断缩小最优解的范围,最终获得所述问题的最优解。倘若出现子集的最优解不满足整数界约束的情况,则通过不断增加约束割除松弛问题不包含整数可行解的区域,使所述问题的最优解逐步显现。分枝-割平面法的详细求解步骤如下:

步骤1:将所述问题进行LP 松弛,松弛后初始化空间域Ω0与收敛精度ε,以及初始空间域对应的上界ψlb(Ω0)、下界ψub(Ω0)。

1）若无可行解集,则问题无解,结束计算；

本文以MEG 运行成本最小为目标,优化层根据所建立的状态转移模型采用分枝-割平面法求解式（6）,以此来调控能源单元,使其运行在所期望的状态。求解所得到的各能源单元的出力向量P及运行状态向量V,如式（7）和式（8）所示。

式中:PGT为GT 的发电功率；PGridb为向电网购入的电功率；PGrids为向电网出售的电功率；PBS,c和PBS,d分别为BS 装置的充、放电功率；PEC为EC 的输出功率；HGB为GB 的 产 热 量；HHB为HB 的 输 出 功 率；HTS,c和HTS,d分别为TS 装置的充、放热功率；HAC为AC 的 输 出 功 率；CCS,c和CCS,d分 别 为CS 装 置 的 充、放冷功率。

式 中:vGT为GT 的 运 行 状 态；vGridb和vGrids分 别 为MEG 的购电状态和售电状态；vBS,c和vBS,d分别为BS装 置 的 充、放 电 状 态；vEC为EC 的 运 行 状 态；vGB和vHB分别为GB 和HB 的运行状态；vTS,c和vTS,d分别为TS 装置的充、放热状态；vAC为AC 的运行状态；vCS,c和vCS,d分别为CS 装置的充、放冷状态。

4 算例分析

4.1 算例参数

为了验证本文所提的统一调控架构的可行性,本文利用附录A 图A1 所示的MEG 系统进行算例分析。算例基于日前预测的可再生能源出力和负荷功率的预测值以及电价和天然气价格的信息,以MEG 日运行成本最低为目标,基于所建立的状态转移模型求解未来24 h 各设备的运行计划。其中,假设天然气价格为0.45 元/（kW∙h）,可再生能源和负荷的日期预测数据曲线如图A4 所示。算例中主要参数如附录C 表C1 和表C2 所示。此外,MEG 采用分时电价向大电网进行购售电,分时电价见表C3。

4.2 优化结果分析

4.2.1 日前优化调控结果

日前优化以日运行成本最低为目标,确定了各能源单元未来一天的出力值。本算例仿真在一台处理器型号为Intel Core i5-7200U、内存为8 GB 的电脑上完成。所得优化结果如附录A 图A5 所示。由图A5 可知,系统在运行时能保持电功率、热功率和冷功率实时平衡。因此,优化结果关于横坐标轴对称。

1）在电价低谷时段,由于电价较低,直接从电网购电满足电负荷比GT 发电更经济。因此,优先选择从电网购电满足电负荷需求,不足部分则由GT补充,同时,通过购电对BS 装置充电以储存电能。在电价高峰时段,由于电价较高,为降低系统运行成本,GT 满发,BS 装置放电以缓解供电压力,电负荷主要由GT 和BS 装置放电满足,多余的电能则向电网售电,以获取利润。在电价平时段,负荷主要由GT 和从电网购电来满足。

2）在电价低谷时段,余热锅炉对GT 发电余热进行回收来满足热负荷,不足部分由GB 提供。在电价高峰时段和平时段,由于GT 发电量较大,通过余热锅炉对GT 发电余热进行回收利用更经济。因此,热负荷主要由余热锅炉满足,GB 不工作,多余的热量则由TS 装置储存,在热量不足时段TS 装置则放热以满足热负荷需求。

3）在电价低谷时段,冷负荷主要由EC 供给。在电价高峰时段和平时段,由于电价较高,冷负荷主要由AC 供给,不足部分由EC 补充。CS 装置则在冷量富余时段进行蓄冷,在冷量不足时段进行放冷以满足冷负荷需求。

MEG 中各能源单元的运行状态如附录A 图A6所示。由图A6 可知,信息物理融合的3 层建模与调控架构实现了对MEG 全运行阶段下各类能源单元状态变化轨迹的优化调控,各能源单元在不同的时段运行在不同的状态,以提高系统运行的经济性。

4.2.2 不同调控策略的对比分析

为了将本文所提的基于CPS 的3 层建模与调控架构（以下简称策略1）与传统的优化调度方法（以下简称策略2）［20］进行比较,本节设置如下场景进行对比分析。

1）抗扰动能力分析

设能源单元出力扰动分别为5%和10%时,观察2 种策略下的系统功率偏差率。功率偏差率δ的表达式为:

式中:Pt为t时刻总出力；Pload,t为t时刻实际负荷功率。

结算结果如附录A 图A7 所示。由图A7（a）可知,当扰动为10%时,采用传统的优化调度方法所得到的δ较大,而基于信息物理融合的MEG 优化调控方法得到的δ明显减小。当扰动增大时,传统的优化调度方法所得到的δ进一步增大,而基于信息物理融合的MEG 优化调控方法得到的δ基本保持不变。

2 种策略在整个优化时段内δ的最大值见附录C 表C4。由表C4 可知,本文所提的基于信息物理融合的MEG 优化调控方法相较于传统的优化调度方法在抗干扰能力方面更优。

2）出力平稳性分析

以GT 为例,在风电出力快速波动的场景下,对比2 种策略下能源单元的出力波动情况。由于标准差σ能反映一组数据集的离散程度,用σ反映能源单元的出力波动情况,表达式为:

式中:Pave为能源单元在优化时段内的出力平均值。

以GT1 为例,附录A 图A8（a）为风电机组的输出功率,图A8（b）为GT1 在2 种策略下所得到的优化结果。经计算,GT1 在策略1 下的标准差为75.7,在策略2 下的标准差为123.7。

由附录A 图A8 可知,在传统的调度策略下,σ为123.7,GT 出力波动性较大。本文所提的调控策略下σ为75.7,表明GT 出力在优化时段内平稳性更好,这能降低GT 的机械损耗,有利于延长GT 的使用寿命。本文所提策略在应对新能源快速波动性方面比传统的策略更具优越性。

综上所述,基于CPS 的MEG 优化调度通过状态感知、分析、决策和执行4 个环节实现信息系统和物理系统的深度融合,物理系统的运行状态全面实时可知可控,系统各单元协调能力更强,因而在面对新能源出力和负荷不确定时,机组出力相较于传统的调度策略更平稳,抗扰动能力更强。

4.2.3 能量流-信息流-资金流交互影响分析

为了分析在MEG 优化调度过程中,能量流、信息流以及资金流三者之间的交互影响关系,本节设置了3 种场景进行对比分析。场景1 为信息系统正常,场景2 为缺失08:00—10:00 时段的分时电价信息,表现在无法获得该时段的电价信息；场景3 为燃气轮机1 缺失09:00—13:00 时段的运行数据,表现在数据与实际值存在偏差。在3 种场景下的优化运行结果如附录A 图A9 所示。

由附录A 图A9 可知,相较于场景1,场景2 中GB、GT1、BS 装置运行状态以及MEG 购售电状态在多个时段都发生了明显变化,场景3 中各单元运行状态变化较小。其中,不同场景下的运行成本见附录C 表C5。由表C5 可知,场景2 和场景3 下的运行成本相较于场景1 分别提高了2.3%和0.7%。以场景2 为例,场景2 运行成本增加主要原因是在08:00—10:00 时段,BS 装置充电和MEG 向电网购电造成的。具体分析为:08:00—10:00 时段为电价高峰期,BS 装置应放电,MEG 应向电网售电以降低系统运行成本,但由于分时电价信息在该时段缺失,系统无法获取该时段的电价信息,若以前一时刻电价信息为依据进行优化计算,将导致系统购电成本增加。

5 结语

本文提出了一种基于信息物理融合的MEG 统一调控架构,并将该架构应用到MEG 的日前优化调控中,本文主要结论如下:

1）从能量流、信息流和资金流3 个维度描述信息物理融合的MEG,可以综合多种影响因素得到系统最优的调控策略,从而实现MEG 的灵活精准调控；

2）MEG 中的能量流与资金流互为驱动,信息流为二者的支撑；

3）在面对新能源出力和负荷不确定时,基于CPS 的优化调控方法相较于传统的调度策略,设备出力更平稳,抗扰动能力更强。

本文所提方法为将CPS 理论应用到优化调度中的一种尝试,可以为MEG 的优化运行提供一定的指导,未来研究将进一步考虑多时间尺度间的协调优化调度。

本文研究得到南方电网数字电网研究院有限公司科技项目(YTYZW20010)的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。