基于机会约束规划的智能楼宇与社区综合能源系统协调优化

周承翰，贾宏杰，靳小龙，穆云飞，余晓丹，宋 毅

（1.智能电网教育部重点实验室（天津大学）,天津市 300072；2.国网经济技术研究院有限公司,北京市 102209）

0 引言

2016 年《中国建筑节能年度发展报告》显示,中国楼宇耗能约占全社会总能耗的23%［1］,其中用于供冷及供热的能耗约占楼宇总能耗的50%。因此,如何充分发掘楼宇的节能减排潜力从而降低其能耗受到了广泛关注。社区综合能源系统（integrated community energy system,ICES）通过多种能源耦合设备［2-4］,可以根据用户需求进行不同能源形式（电、气、热等）的集中转换,高效经济地满足楼宇用户的能源需求。而楼宇用户可利用其围护结构的蓄热特性,在满足舒适性的前提下,根据ICES 的供能价格灵活调节其负荷,从而通过需求响应主动参与ICES的优化运行。因此,深入研究ICES 与智能楼宇（intelligent building,IB）的协同优化具有重要意义。

文献［5］基于楼宇蓄热特性,构建了基于楼宇的虚拟储能模型,并参与微网的优化调度,在一定程度上降低了微网的运行成本。文献［6-7］根据楼宇的热动态特性,构建了楼宇空调系统的优化调度模型,充分发掘楼宇的需求响应潜力,降低了楼宇运行成本。然而上述针对楼宇需求响应的研究中,楼宇用户大多被动地对价格进行响应,无法充分考虑ICES运营商和楼宇用户的差异化利益诉求。此外,已有研究多针对楼宇的电需求响应,未考虑其热负荷针对供热系统的热需求响应 （heating demand response,HDR）。

在电力领域,博弈论被广泛应用于不同主体具有差异化利益诉求的决策问题中。ICES 运营商致力于最大化其售能收益,而楼宇用户的目标往往是最小化其用能成本。在能源交易过程中,ICES 运营商首先制定能源价格来指导楼宇用户的需求响应,随后用户响应后的负荷又反过来影响运营商的定价策略。ICES 运营商和楼宇用户存在利益冲突而决策又有明显的先后顺序。因此,宜采用主从博弈模型描述两者间的利益交互关系。文献［8-10］提出一种基于主从博弈的ICES 分布式优化方法,均可有效提升代理商收益并降低用户成本。文献［11］根据用户的综合需求响应,构建一主多从的均衡模型,并应用于多园区ICES 中,所提方法在提高代理商利润的同时减少了用户的用能成本。然而上述研究的主从博弈模型并未充分考虑可再生能源出力的不确定性对ICES 优化调度的影响。

鲁棒优化和随机优化是两种常见的处理ICES优化调度中不确定性的方法。相较于鲁棒优化［12］,随机优化利用不确定变量的概率分布对不确定变量进行建模［13］, 降低了决策的保守性。其中,机会约束规划在保证优化调度安全性的同时可以兼顾经济性,被广泛应用于含可再生能源的ICES 优化调度中。文献［14］提出一种分布式机会约束方法来处理ICES 风电出力的不确定性,有效降低了系统成本并在规避风险上有较好的表现。文献［15］针对ICES中负荷、风电、光伏出力的不确定性,提出了机会约束最优潮流模型,并探讨了不同置信水平下的系统优化方案。然而［14-15］忽略了IB 的蓄热特性,没有充分考虑IB 提供的需求响应对于ICES 优化调度的影响,无法兼顾代理商和用户的利益。

综上所述,本文首先基于楼宇的热惯性,针对楼宇用户和ICES 的差异化利益诉求,构建了以ICES运营商为上层领导者、用户为下层跟随者的主从博弈双层优化模型。其次,为应对风光出力的不确定性,采用机会约束规划方法,将含随机变量的机会约束转化为确定性约束,从而整合到主从博弈优化调度模型中,并最终转化为混合整数线性规划模型。最后,通过算例分析验证了所提方法的有效性。

1 IB 与ICES 的主从博弈协同优化调度框架

基于主从博弈的IB 与ICES 的协同优化调度框架如图1 所示。其中,ICES 运营商作为领导者,楼宇用户作为追随者。ICES 运营商配备了分布式风电、分布式光伏、储能系统（energy storage system,ESS）、热电联产（combined heat and power,CHP）机组和热泵等多种能源生产和转换设备。楼宇室内安装了带调节阀的智能散热器,可在用户的舒适温度范围内调节其热负荷,从而提供HDR。

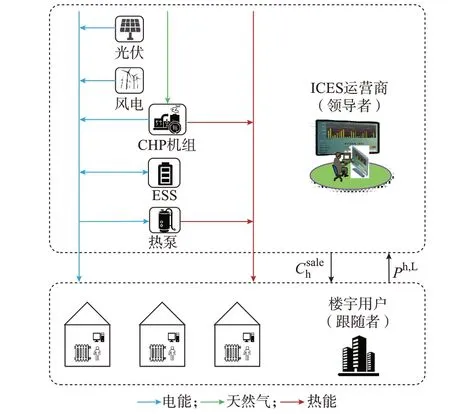
图1 IB 与ICES 的协同优化调度框架Fig.1 Framework of cooperative optimization dispatch between IB and ICES

ICES 运营商和楼宇用户是独立的利益主体。上层ICES 运营商作为领导者,通过优化能源购置策略和制定售热价格以最大化其收益；下层楼宇用户作为追随者,根据ICES 运营商制定的售热价格,提供HDR 以最小化其用能成本。因此,ICES 运营商在制定售热价格时要同时考虑自己的利益和楼宇用户的响应结果,即ICES 运营商和楼宇用户之间存在利益博弈。

由于风光出力的不确定性,ICES 需通过ESS提供备用来保证系统安全稳定的运行。本文将风电和光伏出力视为随机变量,备用约束条件以满足一定的置信水平来表示。置信水平的高低反映了ICES 运营商对系统安全性和经济性的权衡。ICES运营商需要根据系统实际运行状况,选择合适的置信水平,在保证系统安全性的同时兼顾其经济性。

2 基础模型

2.1 楼宇侧模型

本文基于热阻-热容（resistor-capacitor,RC）网络［16］模型来模拟楼宇围护结构的热动态过程。单个制热区域的RC 网络如图2 所示。R表示热量在建筑材料和室内空气中的传输,C表示热量在建筑材料中的存储。其中,制热区域1 为节点1,温度为Tr,制热区域周围的其他空气节点（分别为节点2、3、4、5）,温度分别为T2、T3、T4、T5。用户通过调节散热器阀门（图2（b）红圈处）的开合度来控制散热器流量,使室内温度维持在舒适范围内。

图2 IB 的RC 网络模型Fig.2 RC network model of IB

单个制热区域的热平衡约束如式（1）和式（2）所示:

2.2 ICES 运营商模型

1）ICES 电热平衡

ICES 的电平衡、热平衡如式（7）和式（8）所示:

2）售热价格约束

ICES 运营商在制定售热价格时需要兼顾自身和用户的利益。因此,如式（9）所示,售热价格只能在一定范围内波动。此外,为了保证用户在ICES运营商中购买热能的意愿,运营商制定的热价不应高于用户直接在上级能源系统买热的价格,如式（10）所示。

式中:M为一个足够大的正整数。

风电和光伏出力具有不确定性,ESS 需提供备用来避免系统失负荷,如式（28）至式（29）所示。由于风电和光伏出力预测误差（ΔPwpt、ΔPpvt）是随机变量（相互独立）,因此难以用确定性约束表示含随机变量的约束。本文使用机会约束,来表示约束条件在一定置信水平下成立,如式（30）和式（31）所示。当置信水平为1 时,表示系统没有任何潜在的风险。这样虽然确保了系统的安全,但牺牲了较多经济效益。因此,ICES 运营商需选择合适的置信水平,兼顾其运行的安全性和经济性。

3 基于机会约束规划的IB 与ICES 主从博弈协同优化数学模型

3.1 机会约束的确定性转化

本文认为ΔPt是正态分布的随机变量［17-18］,分布的期望为0、标准差为δ,分布函数为ϕ。上述机会约束式（30）和式（31）,可以通过寻找概率分位值ϕ-1（β1）、ϕ-1（β2）转 化 为 确 定 性 约 束 式（33）和 式（34）,从而方便在优化问题中求解。

式中:δwp和δpv分别为风电和光伏出力预测误差的标准差。

如式（34）和式（35）所示,ICES 运营商可以在置信水平β1、β2下,通过ESS 正负备用的及时调整,应对风光出力的不确定性,保证系统稳定安全运行。

3.2 领导者模型——ICES 运营商的优化模型

ICES 运营商向上级能源系统购买电、热、气,再通过综合能源转化设备为楼宇用户供能。运营商的目标是最大化其收益,需满足ICES 电热平衡约束、售热价格约束、各设备运行约束、机会约束、配电网约束以及供热网约束,如式（36）所示。其中,配电网约束［18］及供热网约束［19］及其线性化方法见附录A第A1 章和第A2 章。

3.3 跟随者模型——楼宇用户的优化模型

楼宇用户的目标是最小化其用能成本,需满足室内热平衡约束、散热器流量约束以及室内温度约束:

3.4 主从博弈优化模型求解

主从博弈可以视作是领导者在上层、跟随者在下层的双层问题,进而用双层优化的方法来解决上下层不同主体存在差异化利益诉求的问题。本文构建的主从博弈双层优化模型中,上层领导者为ICES运营商,下层跟随者为楼宇用户。下层楼宇用户在做决策时,售热价格认为是固定的,下层问题可看成线性问题。当下层问题为线性时,双层问题可以通过构建拉格朗日函数和库恩-塔克（KKT）条件［20-21］将下层问题的目标函数和约束条件转化为上层问题的约束条件,从而将双层优化问题转化为单层带有平衡约束的问题（MPEC）模型。下层问题的KKT条件如附录A 第A3 章所示。此时,整个优化问题的目标函数为上层问题的目标函数,即式（36）中的目标函数。其中的Csaleh,t Ph,Ln,t为两个变量相乘的形式,因此转化后的单层MPEC 模型目标函数是非线性的。考虑到下层目标函数同样含有,而下层问题又为线性问题,可以运用强对偶原理［22］,将下层问题的目标函数转化为相应对偶问题的目标函数EDual,innern,从而线性化式（36）中的非线性项。下层问题目标函数与对偶问题目标函数的对应关系见附录A 第A4 章。经过以上数学变化,原双层优化问题转化为单层线性化问题,从而方便求解。基于主从博弈的双层优化模型及求解流程如附录B 图B1 所示,最终转化得到的混合整数线性规划（MILP）模型如式（38）所示,其中,EDual,innern见式（A32）。

4 算例分析

4.1 算例数据

本文用图1 所示的ICES 算例来验证所提方法的有效性。算例中楼宇设置为层高3 m,共10 层的独栋住宅。每层有4 个用户,每个用户的制热区域为36 m2。选取中国北方冬季的典型日,单个制热区域 的 相 关 参 数［23］、ICES 中 的ESS 参 数 见 附 录B 表B1 和表B2。室外温度［24］和太阳辐射强度［25］、单个制热区域室内的热量［2］、风电预测出力［26］、光伏预测出力［27］以及运营商和用户分别从上级能源系统购买能源的价格见图B2 至图B6。本文没有考虑楼宇电需求响应对售电价格的影响,运营商向用户的售电价格假定为用户从上级能源系统的购电价格,单户居民电负荷［28］见图B7。算例配置了17 台风机、10 台光伏,一个调度周期为24 h,热价每小时变化一次,用户散热器流量每小时变化一次。

4.2 算例分析

4.2.1 主从博弈协同优化调度结果

首先在机会约束置信水平为0.9 的情况下,探讨主从博弈策略下ICES 运营商和用户的协同优化效果。ICES 运营商根据楼宇用户的能源消耗和上层能源系统的能源售价,结合楼宇用户的HDR,优化运营商的能源调度及售热价格。图3 给出了ICES 电能、热能供需平衡结果。

图3 ICES 运营商的能量调度Fig.3 Energy dispatch of ICES operator

如图3（a）所示,在03:00—07:00、09:00 风电多发时段,用户的电负荷均由风电供给。在10:00—12:00、19:00—21:00 时段,风光出力不能满足电能需求,此时由于电价较高,ICES 运营商倾向于向上层购气,并调度CHP 机组来填补电能缺额。如图3（b）所示,热泵的产热效率较高,因此ICES 运营商在大部分时段优先调度热泵来供热。在09:00—10:00 时段,热价较低,运营商倾向于直接购热使用。但是09:00 时,由于风光出力充裕,多出的电能供给热泵产热。在10:00—12:00、19:00—21:00 时段,虽然热泵的产热效率更高,但是如果调度热泵,CHP 机组供电同时产生的热能则无法消耗,从而造成浪费。此外,ESS 也会根据电价进行削峰填谷。在10:00—11:00、19:00 时段,电价较高,ESS 放电；在16:00、23:00—24:00 时段,电价较低,ESS 充电。

用户根据ICES 运营商制定的售热价格相应地调整散热器流量来降低成本,用户的HDR 反过来也会影响售热价格的制定。图4 给出了用户室内散热器流量与售热价格的关系,相应的室内温度变化见附录B 图B8。用户调节室内散热器流量时会引起社区供热网络水流量、水压的改变,本文采用的是集中量调节的方式,热网的水流量变化与用户侧流量变化基本一致。热网的管道压降如附录A 式（A10）所示,图B9 给出了主管道压降和用户散热器流量的变化。

图4 室内散热器流量与售热价格的关系Fig.4 Relationship between indoor water flow rate of radiator and heating sale prices

如图4 所示,在05:00、08:00、13:00 和17:00 时刻,售热价格处于高峰时段,散热器的流量明显降低。相反,当售热价格处于低谷时段（04:00、07:00和16:00）,散热器流量相应升高。此外,室内温度在05:00、08:00 和17:00 时刻达到峰值,对应出现在散热器流量明显升高的后一个时段。这样就可以利用楼宇的热惯性,在售热价格低的时候储热,相应地在热价高的时候可以减少散热器流量,降低供热成本。

为了分析楼宇热惯性对ICES 运营商和楼宇用户主从博弈协同优化的影响,本文按照相同的模型和方法设置了以下两个场景。

场景1:在ICES 运营商和楼宇用户的主从博弈协同优化中考虑楼宇热惯性（用户设定的室内舒适温度范围为22～24 ℃）。

场景2:在ICES 运营商和楼宇用户的主从博弈协同优化中不考虑楼宇热惯性（用户设定的室温恒为22 ℃）。

附录B 图B10 给出了两种场景下散热器流量随时间的变化结果。场景2 中温度保持恒定,室外温度低时提高散热器流量,室外温度高时降低散热器流量,散热器流量不能和热价形成互动,从而无法提供HDR。场景1 与场景2 相比,可以通过调节热价,利用楼宇的蓄热特性,在风电多发时段（红圈处）,加大散热器流量的调节,从而充分利用楼宇热负荷的灵活性来消纳风电。在光伏出力充裕的时段（12:00—14:00）,用户的电热需求也可以充分消纳光伏出力,因此没有弃光的情况。

表1 给出了两种场景下的经济效益以及风光消纳情况。如表1 所示,场景1 的ICES 运营商收益比场景2 高2.26%,且场景1 的单个用户的用能成本比场景2 低0.25%。此外,场景1 的弃风量是场景2 的38.35%,大大改善了弃风情况。充分发掘楼宇的蓄热特性,灵活调节楼宇空间热负荷,可以有效降低用户的用能成本,并促进风光消纳,进而增加ICES 运营商的收益。

表1 两种场景下的优化结果Table 1 Optimization results in two scenarios

4.2.2 不同置信水平下的主从博弈协同优化调度结果

为了说明本文方法的有效性,算例设置了置信水平β分别为70%、90%和98%的机会约束规划场景。ESS 在风光多发的时段可以消纳风光,同时为ICES 提供备用,从而在风光出力波动时保证ICES的安全运行。置信水平的差异会影响ESS 的荷电状态（state of charge,SOC）,进而反映在ESS 的优化调度上。图5 给出了不同置信水平下的ESS 出力（放电为正、充电为负）和剩余电量。附录B 图B11给出了不同置信水平下的弃风量。

在01:00—02:00 时段,虽然电价较低,ESS 仍处于放电状态（如图5（a）所示）,以保证在接下来的风电多发时段有足够的容量进行风电消纳。

图5 不同置信水平下的ESS 的充放电功率和剩余电量Fig.5 Charging/discharging power and dump energy of ESS at different confidence levels

在03:00—07:00 时段,由于风电出力充裕,ESS 多处于充电状态来消纳多发的风电（如图5（a）所示）,总体可看作一个充电时段。同时,在置信水平70%、90%、98% 下,ESS 充电量逐渐减少（如图5（b）所示）,弃风量则逐渐增加。以置信水平98%为例,在充电时段开始（03:00）时,由于负备用约束限制,ESS 的初始电量最高,而在在充电时段结束（07:00）时,由于正备用约束限制,ESS 电量最低。由此说明,置信水平为98%时,ESS 在该充电时段的充电量最少,弃风量最多。此外,置信水平为98%时,由于备用约束的限制,ESS 无法完全消纳03:00—07:00 时段多发的风电。因此,ESS 选择在其中电价较低且具有负备用裕量的06:00 放电,以降低成本。

在10:00—11:00、19:00—21:00 时 段,由 于电价处于峰值,ESS 处于放电状态。在15:00—16:00、23:00—24:00 时段,电价处于低谷,ESS 处于充电状态。而置信水平为98%时,由于负备用约束的限制,在10:00—11:00 时段,放电量明显下降。

综上所述,置信水平越高,对ESS 的备用要求越高,从而影响ESS 的削峰填谷和风光消纳。

4.2.3 不同置信水平的经济性影响分析

如4.2.2 节所示,不同置信水平下ESS 的出力情况不同,进而会影响IB 与ICES 协同优化的经济性。表2 给出了ICES 运营商收益、ESS 备用成本、ICES弃风成本。

表2 不同置信水平的经济性分析Table 2 Economic analysis at different confidence levels

如表2 所示,随着置信水平的升高,ICES 运营商收益逐渐下降,ESS 备用成本和ICES 弃风成本逐渐上升。其中,置信水平从70% 增长到95%,ICES 运营商收益下降了2.73%；而置信水平从95%增长到100%,ICES 运营商收益下降了4.86%。当置信水平较高时,提升置信水平,ICES 运营商的收益会明显下降。类似地,ESS 备用成本、ICES 弃风成本在置信水平从70%增长到95%时,增长缓慢,而置信水平从95% 增长到100% 时,成本陡然增加。ICES 运营商可以根据系统实际运行水平,选取合适的置信水平,在保证安全运行的前提下,避免置信水平过高带来的高额成本。

5 结语

本文提出了一种基于机会约束规划的IB 与ICES 主从博弈协同优化调度方法,兼顾楼宇用户和ICES 运营商的利益,充分挖掘供需两端的灵活性,并进一步分析了不同置信水平下ESS 备用约束对于IB 与ICES 协同优化经济性的影响。所得结论如下:

1）IB 由于热惯性具有一定的蓄热能力,用户通过散热器调整热负荷避开高峰时段,可以进一步降低用户的用能成本,并使室内温度维持在用户舒适的范围。

2）ICES 运营商和楼宇用户是供需端不同的主体,两者之间利益交互,决策又相互影响。本文基于主从博弈的方法,使双方共同参与ICES 定价过程,实现供需两侧的利益均衡。

3）考虑到风电和光伏出力的不确定性,ESS 需提供备用来保证系统安全运行,适当地降低备用约束置信水平,可以使ICES 的优化运行更具经济性。在95%的置信水平下,ICES 运营商收益比100%的置信水平下增加了4.86%。

本文采用的是集中管理方式,将楼宇用户聚合在一起看成楼宇集群,对于不同用户之间的差异性暂未考虑。未来工作会进一步详细考虑差异化用能需求的楼宇和楼宇集群,采用分布式能量管理方法在协同优化中进一步研究多个差异化楼宇用户和运营商的主从博弈分析。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。