直流微电网DAB 变换器和直流固态变压器的非线性控制策略

孟祥齐，贾燕冰，任春光，韩肖清，武 涵，赵 佩

（电力系统运行与控制山西省重点实验室（太原理工大学）,山西省太原市 030024）

0 引言

直流系统以其结构简单、能量转换环节少、控制方式灵活、无须考虑无功和频率问题等优点受到越来越多的关注［1］。分布式电源及直流负载通过变换器构建小型直流微电网,可实现分布式电源与直流负荷自治运行,将成为构建新型电力系统的重要组成部分［2］。而当直流微电网系统所带负载为恒功率负载（constant power load,CPL）时［3］,由于CPL 负阻抗特性,系统受到扰动时相当于正反馈,将对系统的稳定性产生不良影响［4］,研究分布式电源和CPL构建的小型直流微电网的稳定控制策略,对于提升新型电力系统运行稳定性具有非常重要的现实意义。

针对CPL 负载下直流系统稳定问题,现有研究通过在直流母线上增加大容量储能设备［5］或增加电容［6］、减小电感［7］等方式解决,但增大了系统的损耗和使用成本。通过改进变换器的控制策略以提升直流微电网的运行稳定性是目前较为有效的解决策略之一。自抗扰控制［8］、直接功率控制［9］、虚拟电阻控制器［10］等线性控制策略在遭遇CPL 大信号扰动时,不能保证全局稳定。为提升变换器的稳定性,模型预测控制［11］、滑模控制［12］和非线性反馈控制［13］、脉宽调制（PWM）非线性控制［14］等非线性控制方法逐步得到应用,但输出电压的跟踪精度及系统的效率有待提高。反步控制是一种有效改善跟踪精度和系统效率的非线性控制方法［15］,但需对系统不确定性扰动进行准确估计,以减小跟踪误差［16］。观测器技术是一种估计不确定扰动的有效方法,并且不需要额外的传感器,在非线性系统中采用非线性扰动观测 器（nonlinear disturbance observer,NDO）［17］为 抗干扰和不确定性补偿提供了一种很有前景的解决方案。文献［18］采用了NDO 和反步控制方法提高传统Boost 变换器系统的大信号稳定性。随着电力电子技术的发展,双有源全桥（dual active bridge,DAB）变换器由于其电气隔离、功率密度高、能量双向流动、模块级联容易等优点［19］,逐步替代了经典的Buck、Boost 等传统直流变换器；在输入电压高、输出电流大的场合中,由DAB 级联而成的直流固态变压器（DC solid state transformer,DCSST）转换效率更高［20］,得到了广泛的应用［21］。然而,现有文献对带CPL 的DAB 变换器和DCSST 微电网系统的稳定控制鲜有研究,亟须针对带CPL 的DAB 变换器及由DAB 模块级联而成的DCSST 的稳定控制策略进行深入研究。

本文针对带CPL 的DAB 变换器及DCSST 微电网系统提出了一种非线性控制策略。建立了DAB 变换器和DCSST 数学模型的布鲁诺夫斯基标准型；构建了不确定大信号扰动的NDO 估计模型,提出基于NDO 和反步控制的非线性控制策略来提高DAB 变换器及DCSST 在CPL 大信号扰动下的稳定性,并深入分析反步方法与传统比例-积分（PI）方法在大信号扰动下的稳定性区别,针对级联结构DCSST 加入输入均压补偿控制策略以保证多DAB模块间功率均衡,并且分析了输入均压方法对反步控制方法的影响。实验结果表明,采用本文所提新型控制策略,DAB 变换器及DCSST 可以在大信号扰动和不同工作情况下实现系统稳定运行,并且准确地跟踪输出电压参考值。

1 带CPL 的直流变换器数学模型

小型直流微电网系统中,变流器负载、逆变器电机驱动等负荷被严格控制,表现为CPL 特性,由于其负阻抗特性,当发生扰动时,其正反馈增强扰动信号,导致系统的稳定性进一步受到威胁。本文采用反步控制方法解决由带CPL 引起的DAB 变换器和DCSST 微电网系统运行不稳定问题,本章首先构建了DAB 变换器和DCSST 数学模型的布鲁诺夫斯基标准型。

1.1 带CPL 的DAB 变换器及DCSST 拓扑结构

带CPL 的DAB 变换器及DCSST 拓扑结构如图1（a）和（b）所示。DCSST 由n个功率参数相同的DAB 模块通过输入串联输出并联（input-series output-parallel,ISOP）级联而成。在图1（a）和（b）中:us为输入电压源；Rs为输入电阻；R为电阻负载；ui和uo分别为输入和输出电压；ii和io分别为输入和输 出 电 流；uim和iim分 别 为 第m个（m=1,2,…,n）DAB 模块的输入电压和电流；uom和iom分别为第m个模块的输出电压和电流。

DAB 模块拓扑如图1（c）所示,Ci和Co分别为输入电容和输出电容。一般地,DCSST 中各个DAB模块的输入电容Cim和输出电容Com都是相同的。k为高频隔离变压器（T）变比,L为电感。DAB 变换器的功率流动由两个全桥之间的移相比d调节,从而保持输出电压uo稳定。

图1 带CPL 的DAB 变换器和DCSST 的拓扑结构以及DAB 模块拓扑Fig.1 Topological structures of DAB converter and DCSST with CPL and topology of DAB module

CPL 的电压和电流特性可以描述为:

式 中:PCPL为CPL 的 功 率；uCPL和iCPL分 别 为CPL 的电压和电流的瞬时值。

1.2 DAB 变换器的布鲁诺夫斯基标准型

DAB 变换器的状态空间平均模型为［22］:

式中:f为DAB 变换器的开关频率。电感电流平均值在一个开关周期内为零［23］。因此,未考虑电感的状态。

反步控制需构建如式（4）所示的布鲁诺夫斯基标准型:

式中:xm为状态量:cm为不确定项:u为输入控制量。

将DAB 系统中存储的总能量设置为状态量x1,表示为:

对式（5）求导可得:

根据式（4）和式（9）,控制量u和不确定项c2表示为:

根据DAB 变换器的传输功率与移相比d的特性曲线［24］,DAB 变换器的传输功率和移相比特性曲线关于d=0.5 对称,根据式（15）,移相比d的解关于d=0.5 对称。因此,式（15）的两个d的解均为可行解。

1.3 DCSST 的布鲁诺夫斯基标准型

DCSST 中各DAB 模块的状态空间平均模型为:

由式（20）—式（23）可得,DCSST 的等效状态空间平均模型与式（2）、式（3）相同,DCSST 其余推导过程如式（5）—式（15）所示,DCSST 标准型表达式如式（12）所示。

2 复合非线性控制策略

为提升大扰动下系统的稳定性和跟踪精度,本章将NDO 与反步控制相结合,提出了DAB 变换器和DCSST 的复合非线性控制策略。设计了NDO对不确定的非线性扰动和状态量x1的参考值进行估计,在此基础上采用反步控制来保证DAB 变换器和DCSST 在大信号扰动下的稳定性。针对DCSST,添加输入均压补偿控制器,保证每个DAB 模块间功率均衡。

2.1 NDO 设计

由1.2 节和1.3 节推导可知,DAB 变换器和DCSST 中,x1的参考值x1b与负载功率的参考值Pref有关,但是Pref是不确定的,随着PCPL的变化而变化,同样,不确定项c1和不确定项c2也包含PCPL。因此,可以通过估计c1和c2来估计PCPL和x1b。本文利用NDO 来估计c1、c2和x1b,并将其输入至反步控制器。

在实际中,由于c1和c2与负载功率有关,所以它们的值是有界的。c1和c2的导数也是有界的。当系统处于稳态时,负载功率是稳定的。可以假设:

由式（24）可知,c1和c2的导数趋于零。因此,根据式（29）和式（30）可知c͂1和c͂2是收敛的。

x1的参考值可以表达为:

根据式（8）和式（32）,可将Pref表达为:

由式（25）、式（26）、式（36）可知,NDO 可以估计得到ĉ1、ĉ2、x1b。

2.2 反步控制策略

由式（12）所示的布鲁诺夫斯基标准型状态方程 和NDO 的 输 出ĉ1、ĉ2和x1b,设 计 反 步 控 制 策 略 以得到控制信号d。

状态量x1和x2与其参考值x1b和x2b之间的误差为:

由式（39）和式（43）可知,V1（e）正定,V̇1(e)负定。故可知式（37）稳定。

步骤2:设计u使e2=0。

根据李雅普诺夫函数定义能量函数V2（e）为:

根 据 式（37）、式（38）、式（42）、式（51）、式（13）—式（15）,可通过反步控制求得移相比d。基于反步控制和NDO 的DAB 变换器控制策略如图2所示。

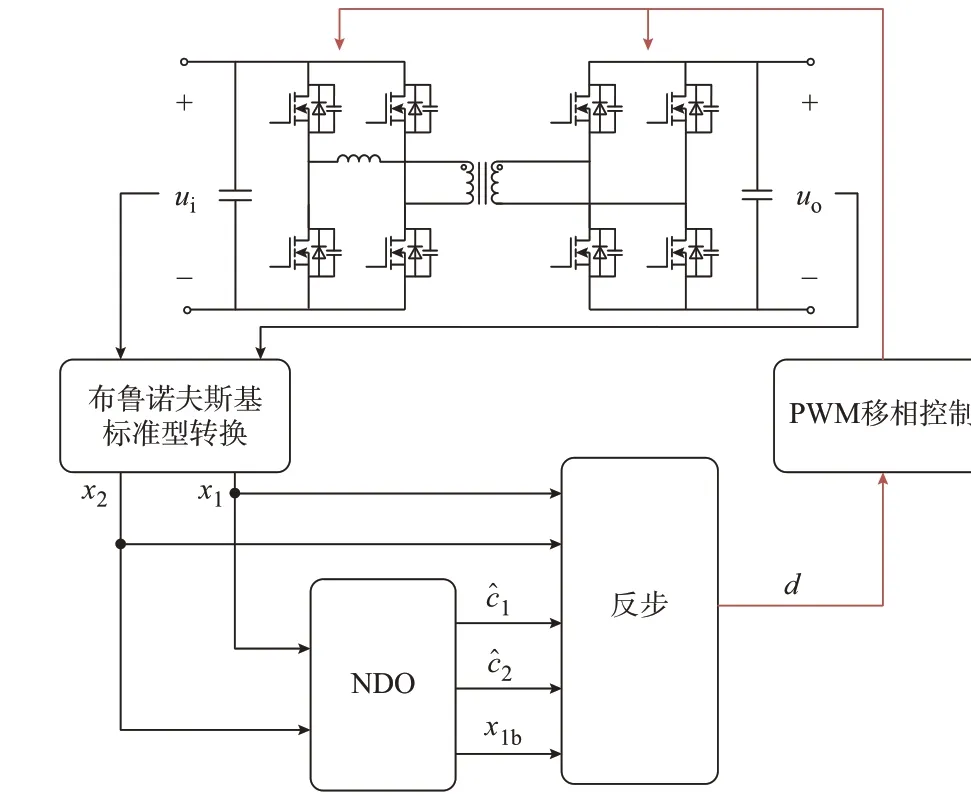
图2 DAB 变换器的NDO 和反步控制策略Fig.2 NDO and backstepping control strategy of DAB converter

首先,由式（5）和式（7）分别求出状态变量x1和x2,得到DAB 变换器的布鲁诺夫斯基标准型；接着,将x1和x2输入NDO,由式（25）和式（26）分别求出c1和c2的 观 测 值ĉ1、ĉ2,由 式（36）得 到x1的 参 考 值x1b；随后将状态变量x1、x2和NDO 输出值输入至反步控制器:先由式（37）和式（38）分别求出误差e1和e2,由式（42）设计x2的参考值x2b；然后,由（51）求出控制量u,最后由式（13）—式（15）得到DAB 变换器的控制信号d。根据DAB 变换器单移相控制策略［24］,调节变换器系统的功率流动以维持电压稳定。

基于反步控制的变换器系统是渐近稳定的,即输出电压uo可以稳定地跟踪uo,ref。

反步控制稳定性证明如下。

对式（37）求导,得到:

根据式（56）和式（57）,特征值均小于零。系统的平衡点可以表示为:

根据式（58）和式（59）,状态量x1和x2可以稳定地跟踪其参考值。基于反步控制的变换器系统是渐近稳定的。根据式（36）,输出电压uo可以稳定地跟踪uo,ref。

2.3 DCSST 的输入均压补偿

在DCSST 中,当各DAB 模块间功率不均衡时,各模块间输入电压存在差异［25］,系统会产生额外的损耗［26］。为了使各模块间功率均衡,在输出电压控制的基础上,加入输入均压控制器补偿,如附录A 图A1 所 示。图A1 中:uirav=ui/n为DCSST 中 第m个DAB 模块的输入电压参考值；G1为输入均压回路中的PI 控制器；Gvd为输入均压控制回路的增益。

通过将DCSST 中每个DAB 模块的输入电压的参考值uirav与实际值uim作差后经过PI 控制器得到式（60）所示的每个DAB 模块的移相比调节信号dam。

式中:kp、ki分别为PI 控制器的比例系数和积分系数。

输入均压控制器的控制带宽远小于本文设计的反步控制,输入均压控制不影响本文提出的基于反步控制的输出电压控制。当本文所提方法在DCSST 中应用时,与DAB 变换器类似,在图2 所示控制模型的基础上,由反步控制得到DCSST 控制信号d后,引入输入均压模块得到每个DAB 模块的移相比调节信号dam,生成DCSST 中每个DAB 模块的最终控制信号,如图3 所示。

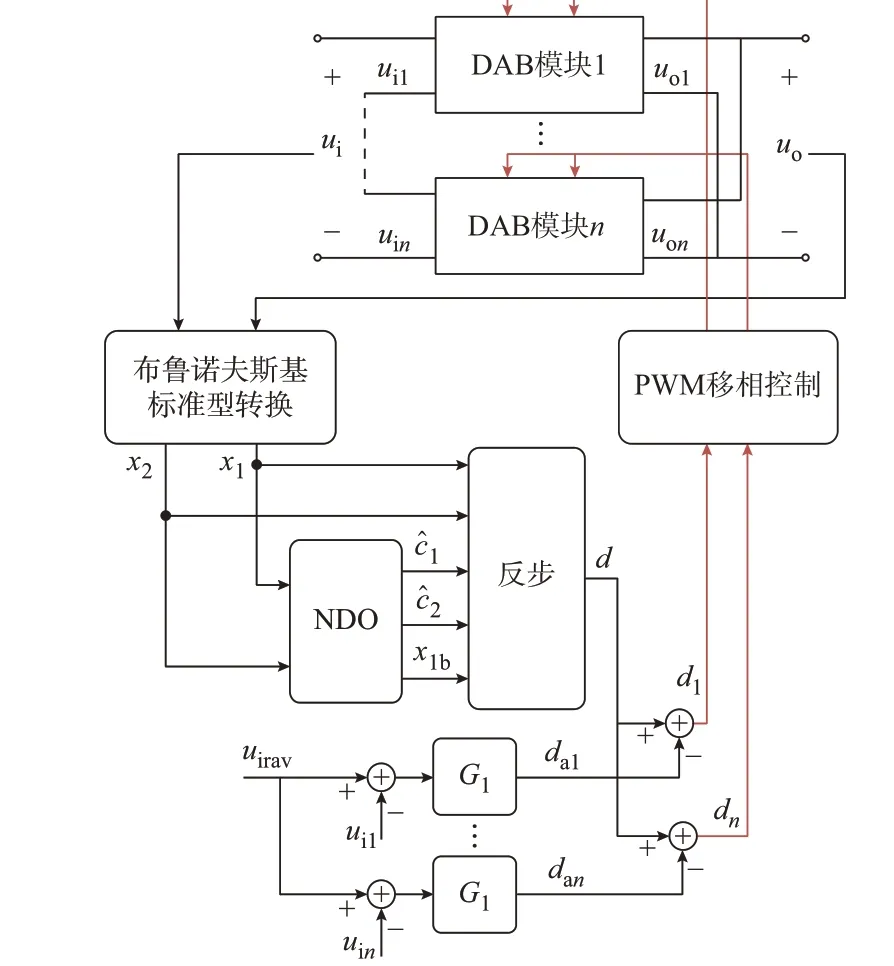
图3 DCSST 带输入均压的反步控制策略Fig.3 DCSST backstepping control strategy with input voltage equalization

2.4 控制参数选取

由于NDO 为反步控制提供参考信号,需要首先设置NDO 的参数l1和l2,并且其动态响应要快于反步控制电压跟踪的动态响应。

当负载由100 W 变化至500 W 时,NDO 的动态响应见附录A 图A2 和图A3。图A2 中:参数l1分别选取为1 000、700、500,参数l2为固定值300,NDO均能在100 ms 内快速地追踪负载变化,并且随着l1的取值越大,其收敛速度越快。图A3 中:参数l2分别 选 取 为1 000、500、300,参 数l1为 固 定 值1 000。由图A3 可看出,NDO 能在25 ms 内快速地追踪负载变化,相比于参数l1,参数l2对系统动态性能几乎没有影响,3 条曲线基本完全重合。

设置不同反步控制的参数k1和k2对输出电压进行仿真。附录A 图A4 和图A5 为当负载由100 W变化至500 W 时输出电压的动态响应。图A4 中:参数k1分 别 选 取 为300、500、800,参 数k2为 固 定 值2 000。由图A4 可看出,随着k1的取值越大,其调节时间越短。图A5 中:参数k2分别选取为1 500、2 000、2 500,参 数k1为 固 定 值500。由 图A5 可 看出,随着k2的取值越大,输出电压的收敛速度越快。

由于反步控制的目的是使得变换器的输出电压能够快速准确地跟踪其参考值,由以上仿真可见,k1和k2越大,性能越好。但值得注意的是,过大的增益将会恶化系统对测量噪声的鲁棒性。因此,需要综合考虑后,选择一个合适的满足系统动态性能要求的控制参数。由于NDO 的动态响应速度要快于电压跟踪速度,本文中电压跟踪速度选择为50 ms 左右,NDO 的收敛速度应为25 ms 左右。经分析,设定NDO 的参数l1和l2分别为1 000、300,反步控制参数k1和k2分别为500、2 000。

2.5 稳定性分析

传统PI 控制方法基于小信号模型,由DAB 变换器的小信号模型［27］及CPL 负阻抗特性［28］可得含CPL 的DAB 系统的传递函数为:

式中:Ui、Uo和D分别为稳态工作点处的输入电压、输出电压和移相比；s为一个具有正实数部分的复变数。

当PCPL增大时由式（61）得出的根轨迹如附录A图A6 所示。由图A6 可知,当PCPL增大时,根轨迹进入右半平面,系统变为不稳定状态。本文采用基于大信号模型的非线性反步控制方法,根据李雅普诺夫稳定性判据,由式（39）—式（50）可得,能量函数V1（e）和V2（e）为:

通过反步控制设计保证了能量函数V1（e）和V2（e）正定,V̇1(e)和V̇2(e)负定,进而保证了系统的平衡点e1和e2等于0。式（52）—式（59）证明了系统的稳定性并可得出系统稳定与PCPL无关。因此,所设计的方法在全局范围内可以保证系统的稳定性。基于小信号模型的线性方法只能保证在稳态工作点附近小范围内稳定,而本文所提基于大信号模型的非线性控制方法可以保证在全局范围内的稳定性。

3 实验验证

本文搭建了包含DAB 变换器和由两个DAB 模块级联而成的DCSST 实验系统,如附录A 图A7 所示。开关管选用CAS120M12BM2 型SiC 金氧半场效晶体管（MOSFET）。dSPACE 用于产生DAB 变换器和DCSST 的PWM 信号。DAB 变换器输入、输出侧额定电压均为100 V；DCSST 输入侧额定电压为200 V,输出侧额定电压为100 V。电感L为20 µH,输入输出电容C为1 000 µF,开关频率f为50 kHz,变比k为1∶1。

为了证明本文所提控制策略的有效性,在以下两种情况下进行实验验证。

1）情况1:为了验证在大信号扰动下,所提控制策略对DAB 变换器和DCSST 的稳定性和动态性能的影响,采用的负载为纯CPL,在t1和t2时刻,CPL 上叠加阶跃变化。

2）情况2:为了验证所提控制方法在不同工况下的稳定性和电压跟踪性能,在t1和t2时刻,CPL 上叠加阶跃变化,同时输出电压参考值变化。

图4 为DAB 变换器在情况1 下的实验波形。CPL 额 定 功 率 为500 W,在t1时 刻 之 前,DAB 变 换器输出侧电压稳定在100 V。在t1时刻,CPL 从500 W 跃变为100 W,在t2时刻,CPL 从100 W 跃变至600 W。为了证明所提控制策略的有效性,在运行情况1 下,本文所提控制策略与滑模控制和PI 控制进行了比较,如附录A 图A8 和图A9 所示。

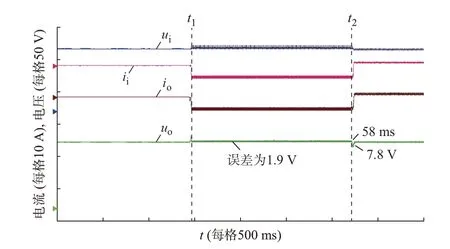
图4 DAB 变换器在情况1 下的实验波形Fig.4 Experimental waveforms of DAB converter in scenario 1

图5 为DCSST 在情况1 下的实验波形,其中:io1和io2分别为DCSST 第1 个和第2 个模块的输出电流；ui1和ui2分别为DCSST 第1 个和第2 个模块的输入电压。CPL 额定功率为1 000 W,在t1时刻之前,DCSST 输出侧电压稳定在100 V。在t1时刻,CPL从1 000 W 阶跃至200 W；在t2时刻,CPL 从200 W阶跃至1 200 W。为了证明所提控制策略的有效性,在运行情况1 下,本文所提控制策略与滑模控制和PI 控制进行了比较,如附录A 图A10 和图A11所示。

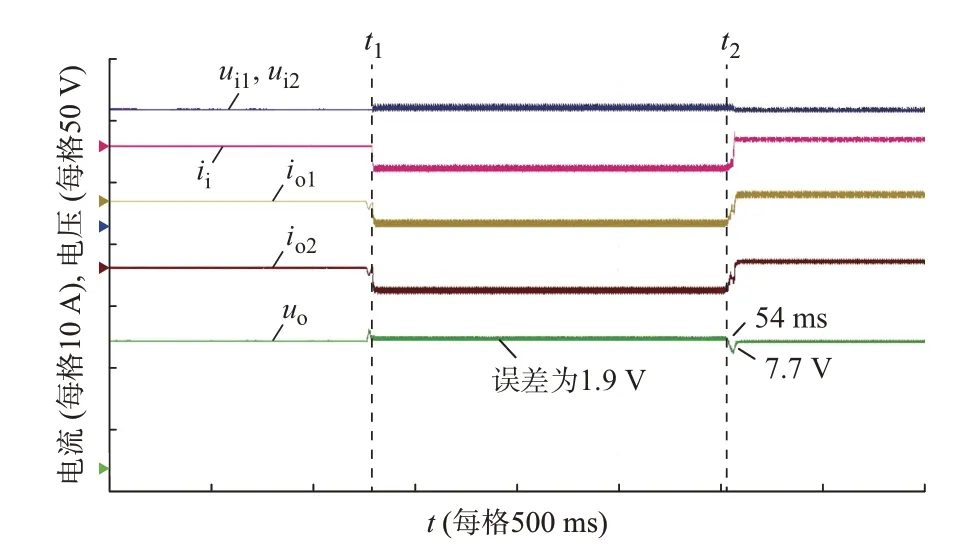
图5 DCSST 在情况1 下的实验波形Fig.5 Experimental waveforms of DCSST in scenario 1

由实验结果可知,PI 控制在CPL 变化时无法保证系统的稳定。滑模控制虽然能够在CPL 变化时保持系统的稳定,但是其动态性能和跟踪精度仍需改善。本文提出的控制方法与滑模控制的平方误差积 分（ISE）、均 方 误 差（MSE）、平 均 绝 对 误 差（MAE）如附录A 图A12 所示。由实验波形和图A12 可知,相比于滑模控制和PI 控制,本文所提控制方法改善了系统的动态性能和跟踪精度,并且保证了系统在CPL 扰动下的稳定性。

图6 为DAB 变换器在情况2 下的实验波形。输出侧额定功率为100 W。在t1时刻,CPL 从100 W变化到500 W,输出电压参考值从100 V 变为90 V。在t2时刻,CPL 从500 W 变化到50 W,输出电压参考值从90 V 变为100 V。由图6 可以看出,DAB 变换器输出电压能够准确、快速地跟踪参考值。当CPL 变化时,DAB 变换器可以保持稳定运行。

图6 DAB 变换器在情况2 下的实验波形Fig.6 Experimental waveforms of DAB converter in scenario 2

图7 为DCSST 在情况2 下的实验波形。输出侧额定功率为200 W。在t1时刻,CPL 从200 W 变化到1 000 W,输出电压参考值从100 V 变化到90 V。在t2时刻,CPL 从1 000 W 变化到100 W,输出电压参考值从90 V 变化到100 V。由图7 可以看出,所提控制策略可以保证DCSST 的输出电压能够准确、快速地跟踪参考值。当CPL 变化时,DCSST 可以保持稳定运行。

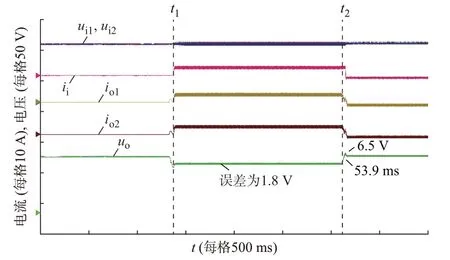
图7 DCSST 在情况2 下的实验波形Fig.7 Experimental waveforms of DCSST in scenario 2

根据以上实验结果,本文提出的控制策略在CPL 变化和不同工况下可以有效地保证DAB 变换器和DCSST 输出电压精确快速调节,并且保持运行稳定。同时,可以保证DCSST 的子模块输入电压均衡,实现各DAB 模块间的功率均衡。

4 结语

本文为提高DAB 变换器和DCSST 在大信号扰动下的稳定性,提出了一种适用于DAB 变换器和DCSST 的NDO 与反步控制相结合的复合非线性控制策略。采用NDO 对不确定的大信号扰动进行估计,建立了基于NDO 及反步控制的非线性控制器,保证了系统的稳定及电压跟踪的快速性和准确性。特别地,针对DCSST 提出了输入均压补偿控制策略,保证了DCSST 子模块功率均衡。实验结果表明,所提控制策略不仅可以准确快速地调节输出电压,并且可以在不同工况下保持系统运行稳定。

本文仅以DAB 变换器及DCSST 为例进行验证,但是所提控制策略适用于其他类型的变换器系统。后续研究可在本文基础上,进一步深入研究所提方法在其他类型变换器系统中的应用。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。