交直流子网双边惯量约束下互联变流器动态功率控制策略

杜 燕，言明明，3，王 鑫，杨向真

（1.合肥工业大学电气与自动化工程学院,安徽省合肥市 230009；2.教育部光伏系统工程研究中心,安徽省合肥市 230009；3.国网江西电力有限公司超高压分公司,江西省南昌市 330096）

0 引言

随着新能源技术与微电网技术的快速发展,具备更高灵活性、可靠性和低损耗的交直流混合微电网（hybrid microgrid,HMG）得到了更多的关注［1-2］。作为交流子网和直流子网能量交互的桥梁,互联变流器（interlinking converter,ILC）在增强子网抗负荷波动能力的同时［3-4］,也会使得交直流子网间的动、静态特性相互耦合。因此,需要根据交直流子网的特性,优化设计ILC 控制器,以保障HMG 的电压、频率性能。

针对ILC 稳态控制的优化,文献［5］提出了归一化下垂控制,实现无通信条件下的网间功率传输。文献［6］则在归一化的基础上构建ILC 指令功率的二次下垂控制,解决多ILC 并联运行时的功率分配问题。针对ILC 会因负荷小功率波动导致运行模式频繁切换的问题,文献［7-8］提出了分段下垂控制策略。而在ILC 的动态优化控制方面,由于ILC 的下垂控制不具备惯量,动态性能较差,文献［9-12］采用含频率变化率（rate of change of frequency,RoCoF）和电压变化率（rate of change of voltage,RoCoV）的ILC 虚拟同步发电机（virtual synchronous generator,VSG）控制方法［9-10］和功率控制方法［11-12］,改善交流频率、直流电压的动态性能。上述文献中仅利用ILC 模拟惯量实现动态功率控制,忽略了子网自身惯量对ILC 功率控制的影响,依旧采用下垂控制描述交直流子网。

随着VSG 技术在分布式电源上的应用［13-14］,子网独立运行时的惯量满足RoCoF/RoCoV 约束要求［15-16］。但子网互联运行后,子网的动态特性会通过ILC 耦合,改变HMG 电压以及频率的动态性能,可能出现ILC 功率振荡超限、系统的RoCoF 和RoCoV 越界等问题［17］。针对该问题,文献［18-19］提出ILC-储能协同控制策略改善HMG 的动态性能,其中储能根据对侧子网的变化率调整输出功率,ILC 仅传递储能产生的额外功率。该方式可提升HMG 的动静态性能,但需增加储能容量以应对对侧功率需求。为发挥ILC 动态功率调节能力,文献［20］提出一种两级ILC 的结构,通过在ILC 内部设置储能,实现交直流子网动态性能的解耦。文献［21-22］则分别考虑交流子网惯量与直流子网惯量的影响,设计ILC 控制参数,但并未在同时考虑双边子网惯量的影响下对ILC 控制参数进行设计。

为实现考虑交直流子网双边惯量影响下的ILC动态功率控制,本文建立了包含交直流惯量的HMG 小信号模型,分析了子网的惯量对HMG 频率、电压动态性能的影响。在归一化下垂控制的基础上提出了考虑双边子网惯量约束的ILC 动态功率控制方法,引入了电压和频率的变化率控制,动态优化子网的等效惯量。以HMG 的电压和频率动态性能、系统稳定性和ILC 最大输出功率为约束,优化设计了所提出的动态功率控制参数,实现了多目标约束下ILC 动态功率控制目标。实验验证了分析的正确性和改进控制的有效性。

1 HMG 互联系统

1.1 HMG 拓扑

附录A 图A1 为典型的HMG 结构,交流子网和直流子网通过ILC 实现互联互济。其中,在孤岛模式下HMG 通过ILC 保证子网的功率平衡,减小直流子网电压和交直流子网频率的波动,提高孤岛HMG 的稳定性和灵活性。

1.2 ILC 结构

ILC 结构如附录A 图A2（a）所示,变流器经过LC 滤波器和线路阻抗Zc=rc+Lc连接至交流母线,其中,rc、Lc分别为线路电感和电阻；直流侧通过直流电容连接至直流母线。

在孤岛模式下,ILC 采用附录A 图A2（b）所示的归一化电压-频率双下垂控制［7］,归一化双下垂表达式为:

式中:x表示ωpll+εac或udc,m-εdc；xmin、xmax分别为x容许的最小值和最大值。

通过式（1）可实现稳态下交流母线频率归一化值ωpu与直流母线电压归一化值upu相等,即ωpu=upu,使交、直流子网按照子网容量承担负荷功率,提高系统承受负荷波动的能力。

2 考虑交直流子网惯量的HGM 小信号建模及特性分析

ILC 采用式（1）的归一化下垂控制,可保证HMG 交直流子网间稳态功率的分担。然而,由于子网间的动态特性通过ILC 相互耦合,交直流子网惯量大小会影响HMG 的动态性能和稳定性。因此,本章给出了含交直流子网惯量的HMG 小信号模型,分析了在归一化下垂的ILC 控制下子网惯量对HMG 系统动态特性的影响。

2.1 含惯量特征的交流子网和直流子网建模

子网的惯量表征子网阻碍电气特征量（直流电压udc和交流频率ωac）突变的能力［23］,限制电气特征量变化过快而影响系统稳定性。为研究交直流子网的惯量对HMG 动态性能和稳定性的影响,可将子网等效为一台同步发电机,统一的外特性方程表示为［11,23］:

式中:H为子网的惯量；y为子网的电气特征量,yN为电气特征量的额定值；PN为子网的额定容量；P为子网实际输出功率；k为子网的下垂系数。

2.2 ILC 建模

ILC 可分为滤波器、电流内环、功率外环和采样环节4 个部分。

1）滤波器采用LC 滤波器,可得到ILC 输出电流、输出电压和电感电流之间的关系,具体如下:

式中:ildq、iodq、uodq分别为电感电流、输出电流和输出电 压 的dq轴 分 量；usdq、ubdq分 别 为ILC 交 流 侧 电 压和交流母线电压dq轴分量；Cf、rd分别为滤波电容和阻尼电阻；rf、Lf分别为交流滤波电感和电阻。

2）电流内环采用比例-积分（PI）控制,具体如下:

4）交流频率、直流电压采样环节:交流频率和直流电压均需要采样,其中频率采样通过锁相环实现,其传递函数见式（13）和式（14）［24］；直流电压采样传递函数如（15）所示；使用低通滤波器表示上述采样环节的延时。

式中:Kp,pll、Ki,pll分别为锁相环PI 控制器的比例系数和积分系数；Ts为采样延时；V为交流母线电压的幅值；Ho（s）为锁相环的开环传递函数。

结合式（1）—式（15）所示方程,建立HMG 的状态方程,并进行小信号处理得到:

式中:Δ 表示变量为小信号形式；A为系统状态矩阵；z为系统状态变量,z=［ildq,iodq,uodq,γdq,γPQ,γ1,2,ωpll,udc,m,ωac,udc,PILC,QILC］T,其中γ1,2为锁相环的中间变量。

2.3 交直流子网惯量对HMG 的影响分析

附录A 图A3 给出了HMG 的状态方程特征值随Hac、Hdc变化的轨迹。特征值共有18个,其中有2个特征值远离虚轴而未标出。从图A3 可以看出,特征值可被分为高频段（λ14～λ16）、中频段（λ10～λ13）和低频段（λ1～λ9）。根据其距离虚轴的距离可知,系统的动态特性主要由靠近虚轴的低频段特征值决定（λ1～λ9）。在Hac、Hdc的 变 化 过 程 中,主 导 特 征 值λ1～λ9中λ1～λ3、λ6～λ9保持为复数实根,而仅有的一对 共 轭 特 征 值λ4、λ5的 阻 尼 比η随 着Hac、Hdc的 变 化而变化,因此可通过分析λ4、λ5的阻尼比η情况判断系统的动态性能。

附录A 图A3（a）中保持Hac不变,Hdc从0.05 kg·m2增加到0.2 kg·m2（箭头方向）,特征值λ4、λ5会逐渐向着实轴靠近,阻尼比先减小后增加。图A3（b）中保持Hdc不 变,Hac从1 kg·m2增 加 到50 kg·m2,特 征 值λ4、λ5会逐渐向实轴靠近,阻尼比增加。

图1 给出了不同Hac、Hdc组合下λ4、λ5的阻尼比η变化规律图,其中蓝线和绿线表示阻尼比区域边界。附录A 表A1 中Hac、Hdc的值在图1 中用红点标出,其位于阻尼比小于0.707 的区域3 中,阻尼比为0.644,这表明虽然子网的惯量能满足子网独立运行的动态性能约束,但互联后HMG 动态性能仍然会出现超调、振荡等问题。而区域1 为阻尼比η=1 区域,此区域内系统无振荡、超调问题,可保证HMG的稳定运行,而此时则需增加Hac才能使得系统从红点（η＆lt;0.707 区域）移动到η=1 区域。因此,图1 表明,即使交直流子网惯量水平满足独立运行的支撑能力,HMG 采用归一化下垂的ILC 控制策略,交直流子网的功率互济仍会造成系统的振荡和潜在失稳风险。

图1 不同Hac、Hdc组合下λ4、λ5的阻尼比Fig.1 Damping ratio of λ4 and λ5 under different combinations of Hac and Hdc

由图1 可知,若希望HMG 运行于区域1 下,则在同样的直流子网惯量水平下,需增加交流子网惯量,这意味着需要增加更多的储能设备。而ILC 可通过模拟同步发电机的惯量,改变子网惯量水平,等效地使得Hac、Hdc由区域3 移动向区域1。

3 考虑子网惯量约束的ILC 动态功率控制策略

3.1 ILC 动态功率控制策略

假设期望子网增加惯量为N/yN,N为子网惯性系数。根据式（3）可得由ILC 传递到单侧的模拟动态功率Pinertia为:

为了分析ILC 在式（18）控制下对子网动态性能的影响,忽略采样环节的影响,并以直流侧为例,将式（18）代入直流子网动态方程中得到式（20）:

式中:PdcN、Pdc分别为直流子网额定有功功率和实际输出有功功率；uN为直流母线额定电压。ΔH可认为是由ILC 动态功率控制获取的等效惯量。因此,式（20）表明采用式（18）的动态功率控制相当于动态调整交直流子网的等效惯量,从而实现动态功率匹配。

3.2 N1、N2的多目标优化设计

上述分析表明ILC 的动态功率控制可等效改变交直流子网的惯量,但由于ΔH受Δωac/Δudc正负的影响,式（18）所示的动态功率控制需要在保证电压、频率跌落率的前提下实现ILC 动态功率控制。为了全面分析N1、N2对系统动态性能和稳定性的影响,用式（19）替换式（1）,重新建立如式（16）所示的小信号状态方程,绘制根轨迹如图2 所示,并以稳定性、动态性能、传输功率能力等为约束条件确定N1、N2的取值范围。

图2 中红圈表示随N1、N2改变特征值的移动方向。图2 表明增大N1、N2使得主导极点中的共轭特征值λ4、λ5向负实轴移动（箭头方向）,增大系统阻尼比,同时特征值λ9向高频移动,脱离主导极点范围；但过大的N1、N2会使得处于中频区域的特征值λ11、λ12向低频移动,影响系统动态性能,甚至越过虚轴,造成系统失稳。图2 表明虽然改变系数能使得系统的动态过程得到优化,但取值过大会引入右半平面特征值（λ11、λ12）,降低系统动态性能,甚至使得系统失稳,因此需要合理选择N1、N2的取值。

图2 动态功率控制下的系统状态方程特征值轨迹Fig.2 Eigenvalue trajectories of system state equations with dynamic power control

1）稳定性约束:系数的取值需要使得系统保持稳定,即所有的特征值都不存在正实部,具体如式（22）所示。

2）动态性能约束:为避免电压、频率的振荡,单侧惯量减小导致的电压、频率超调和越界等问题,将主导特征根设定为过阻尼模式,可得到关于主导特征值λ1～λ8的动态性能约束条件如式（23）所示。同时,为避免特征值λ11、λ12向低频移动,影响系统动态性能,特征值λ11、λ12实部应大于主导极点范围的5 倍［26］,即满足式（24）。

3）功率传输极限约束:ILC 提供的惯量功率最大值应该不超过ILC 的最大功率值。负荷突变时电压或频率变化率最大,因此负荷突变时,可认为仅有动态功率起作用。依据式（18）可知应该满足条件:

式中:PILC,max为ILC 的最大功率。

基于式（22）—式（25）所示约束得到系数N1、N2约束随交、直流子网惯量变化图如图3 所示,其中Hac、Hdc的 取 值 见 附 录A 表A1。图3（a）表 示 保 持Hdc不变,约束随着Hac变化；图3（b）表示保持Hac不变,约束随着Hdc变化。4 个约束曲面以及N1＆gt;0、N2＆gt;0 围成的空间为N1、N2的取值范围（如图3 中红色曲线所示）。

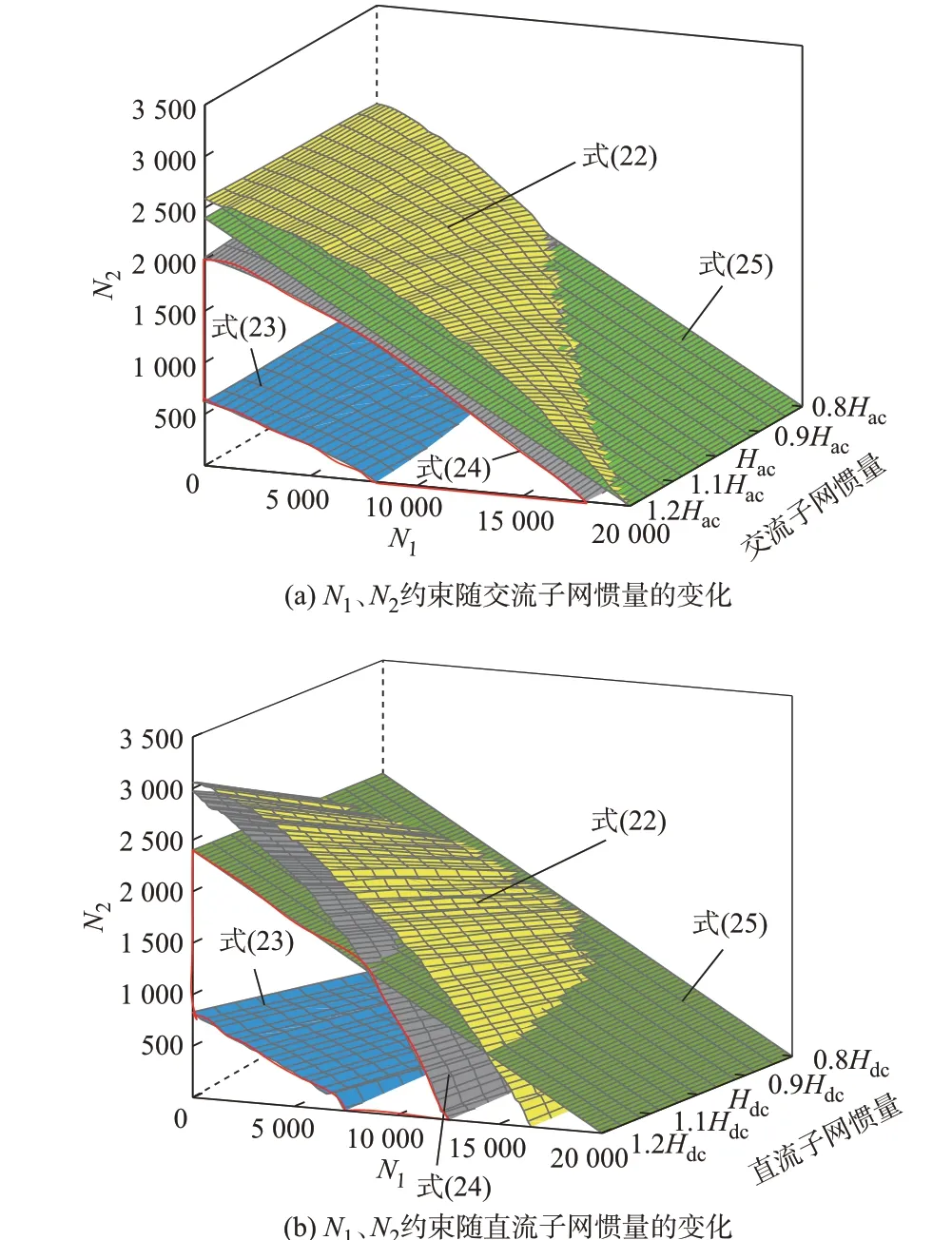
图3 N1、N2约束随交、直流子网惯量变化的情况Fig.3 Variation of N1 and N2 constraints with inertia of AC and DC subgrids

附录A 图A4 给出了采用所提出动态功率控制方式和采用式（1）所示的归一化下垂控制的条件下,HMG 系统的主导极点阻尼比情况,其中,N1=8 750、N2=1 250 根据图3 约束条件获得。由附录A 图A4可以看出,改进后的动态功率控制策略可在不改变交流子网和直流子网自身惯量的情况下,通过动态功率控制实现将阻尼比为1 的边界向左移动,使得附录A 表A1 中Hac、Hdc的组合（附录A 图A4 中红色点）位于阻尼为1 的边界上,实现了改善系统动态性能的目标。

综上,合理地选择参数N1、N2可以改善系统的动态性能,使得HMG 电压和频率的动态性能满足系统约束要求。

HMG 中需综合评估考虑交流子网和直流子网的变化率,为了定量评估越界风险,定义越界风险指标d,评估系统的RoCoF 和RoCoV 的越界风险。d的表达式为:

4 实验验证

为验证本文所提出的惯量补偿策略的有效性和参数选择的正确性,利用附录A 图A5（a）所示的StarSim 平台搭建孤岛运行的交直流HMG 系统,其系统拓扑如附录A 图A5（b）所示,其中直流子网由2 台DC/DC 变流器组成,采用虚拟直流电机控制,交流子网由2 台DC/AC 逆变器等效,采用虚拟同步发电机控制。系统参数如附录A 表A1 所示。

4.1 传统归一化下垂控制下振荡和变化率越限情况

4.2 控制方式验证

为验证ILC 动态功率控制方式的有效性和约束的有效性,通过选取交直流惯性系数N1、N2满足约束条件、不满足动态性能条件、不满足系统稳定性条件3 种情况进行验证。

1）N1、N2满足约束条件（N1=8 750,N2=1 250）

图5（a）和（b）分别给出了交直流子网负荷分时加载和同时加载的系统运行情况,其中负荷变化大小和顺序与图4 相同。和图4 相比,在同样的子网加载条件下,图5 中稳态的ωpu、upu和图4 相同,说明该方法不会影响稳态功率互济结果。

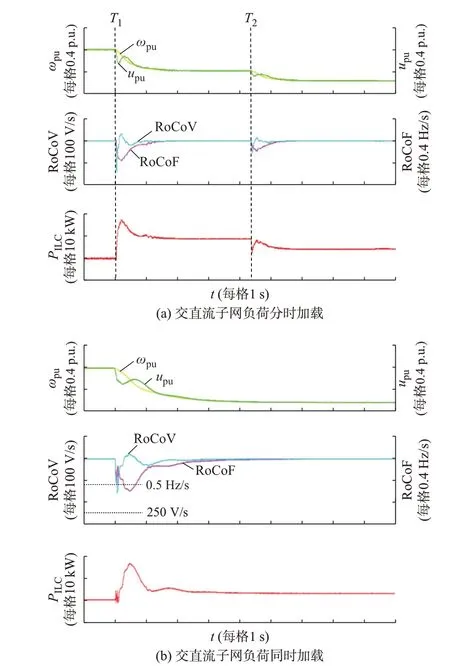
图4 交直流子网互联运行情况Fig.4 Interconnection operation of AC and DC subgrids

图5 ILC 动态功率控制策略Fig.5 Dynamic power control strategy of ILC

2）N1、N2不 满 足 动 态 性 能 约 束（N1=1 200、N2=350）

3）N1、N2不 满 足 稳 定 性 约 束（N1=13 000、N2=900）

附录A 图A8 是系数取值不满足稳定性约束条件的结果。由于参数设计不满足稳定性能约束,T时刻交流侧投入负荷rac=14.5 Ω,直流侧投入负荷rdc=30.6 Ω,负荷加载后1.7 s 系统出现振荡不衰减,随后失稳,导致互联系统崩溃。

5 结语

本文考虑HMG 中子网自身的惯量特征,将子网惯量代入HMG 系统进行小信号建模,并分析交直流子网惯量与系统动态性能之间的规律,证明子网的动态特性会通过ILC 耦合,造成HMG 中交流频率和直流电压动态性能变差,出现电压频率变化率振荡和变化率越界问题。

本文提出的考虑HMG 惯量约束的ILC 动态功率控制策略,可在不影响稳态功率互济情况下解决交直流子网在动态过程中电压、频率振荡和RoCoF、RoCoV 越界问题。以HMG 系统动态性能、稳定性以及ILC 功率限制为约束条件,划定了系数N1、N2的取值范围。通过半实物仿真平台验证了所提控制方式和约束的有效性。而在两侧子网同时近乎满负荷情况下,电压、频率同向变化且接近变化率边界,系统存在变化率越界风险。后续将研究利用交直流子网内部储能,在系统变化率、偏差值接近限值的场景下,通过储能的出力减小越界风险。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。