基于并行多维近似动态规划的综合能源系统动态经济调度

张玉敏，孙鹏凯，吉兴全，杨 明，于一潇，张 旋

（1.山东科技大学电气与自动化工程学院,山东省青岛市 266590；2.电网智能化调度与控制教育部重点实验室（山东大学）,山东省济南市 250061；3.智能电网教育部重点实验室（天津大学）,天津市 300072）

0 引言

新能源的大规模消纳在实现清洁化和低碳化的同时,其出力固有的不确定性为电力系统的经济调度带来新的挑战［1-2］。在综合能源系统（integrated energy system,IES）中,电、气、热能之间具有深度耦合特性及相互转化的潜能。因此,充分挖掘电-气-热多能流的灵活性资源,提高IES 优化调度决策水平,是应对新能源的不确定性、提高新能源消纳水平的有效途径［3-4］。

为此,诸多国内外学者围绕多能耦合的综合能源系统随机动态经济调度（integrated energy system stochastic dynamic economic dispatch,IES-SDED）问题展开了研究。在应对IES 中不确定性方面,随机 优 化（stochastic optimization,SO）［5-7］、鲁 棒 优化［8-10］和分布鲁棒优化算法［11-14］被广泛应用。此外,模型预测控制（model predictive control,MPC）算法由于其对模型的广泛适应性,已被成功应用于IESSDED 问题中［15-16］。然而,MPC 对预测的准确性有较强的依赖,往往难以获得整个调度周期的全局最优解。近年来,基于大数据的智能算法在IES 经济调度中被广泛应用［17-19］,然而其过于依赖训练的数据量,因而影响其工程实用性。此外,上述研究中对不确定性的处理仅局限于单一元素,目前鲜有研究同时考虑风电、电价以及负荷等多元不确定性情况下的IES 随机经济调度问题。

近 似 动 态 规 划（approximate dynamic programming,ADP）算法既兼顾传统动态规划（dynamic programming,DP）算法［20-21］易于获取全局最优解的优势［22］,也利用值函数近似,解决了“维数灾”的问题。现今,ADP 算法已成功应用于电力系统优化调度领域中的储能控制［23］、发电计划制定［24］、机组组合［25］、电动汽车充放电控制［26］以及随机经济调度［27-28］等问题中。然而,目前鲜有研究利用ADP 算法充分挖掘电-气-热多能流中蕴含的灵活性资源。因此,亟须研究一种能够充分发挥多能互补优势的IES 调度策略及高效求解方法。

考虑到电-气-热IES-SDED 是一种多维随机动态规划问题,ADP 算法在保持求解精度的前提下,计算效率会随之降低［29］。并行计算作为一种发展成熟的高效计算技术,其与ADP 算法相结合的并行多维近似动态规划（parallel multi-dimensional approximate dynamic programming,PMADP）算 法已经成功应用于电力系统和水电优化调度领域［30-31］。本文引入PMADP 算法的思想,用于求解电-气-热IES-SDED 问题,主要贡献如下:

1）提出3 层循环嵌套结构的IES-SDED 问题求解框架,使多能耦合IES 优化调度问题的求解与基于并行全局寻优思想的多维近似动态规划求解策略相契合,有效解决了IES 中多元高维数据在离线训练中耗时长的问题。

2）提出状态变量聚合方法,通过构建由高维状态变量聚合到低维状态变量的筛选机制,解决动态规划的“维数灾”问题,提升了求解效率。

3）提出状态空间压缩策略,依据电储能系统（electrical storage system,ESS）和 蓄 热 罐（heat storage tank,HST）决策更新过程中调度基点对搜索空间的影响,剔除无效状态,降低求解规模,在兼顾求解精度的同时显著提升了计算速度。

1 并行多维近似动态规划求解思想

本文提出PMADP 算法对附录A 中构建的IES-SDED 模型进行求解。

1.1 并行多维近似动态规划基本概念的定义

PMADP 模型包括状态变量、决策变量、外部信息及值函数等。为便于理解,结合IES-SDED 问题,给出如下定义。

1）状态变量

状态变量反映了IES 在场景n中时段t的状态:

式中:Sn,t为场景n中时段t的状态；Pg,n,t-Δt、Pc,n,t-Δt和Pk,n,t-Δt分别为场景n中燃煤机组g、热电联产（combined heat and power,CHP）机组c和燃气轮机k在时段t-Δt的出力；Ee,n,t和Hh,n,t分别为场景n中第e个ESS 和第h个HST 在时段t的可用容量；Pw,n,t为 场 景n中 风 电 机 组w在 时 段t的 出 力；Di,n,t、Hf,n,t和Gm,n,t分别为场景n中电网节点i、热网节点f和气网节点m的负荷；pn,t为场景n时段t的电价。

2）决策变量

将场景n中时段t的决策变量xn,t分为xn,t,e、xn,t,gas和xn,t,h3 个部分,分别为场景n中时段t电力系统（electric power system,EPS）、天 然 气 系 统（natural gas system,NGS）和区域供热系统（district heating system,DHS）的决策变量,表达式为:

3）外部信息

外部信息反映了系统的随机性,其由日前预测信息Fn,t及预测误差ΔFn,t两部分组成。在IESSDED 中,本文考虑了风电、电负荷、热负荷、气负荷及电价的不确定性,表示为:

式中:Pw,n,t,f、Di,n,t,f、Hf,n,t,f、Gm,n,t,f和pn,t,f分 别 为场景n中时段t的风电机组w的出力、电网节点i处的电负荷、热网节点f处的热负荷、气网节点m处的气负荷 和 电 价 的 日 前 预 测 信 息；ΔPw,n,t,f、ΔDi,n,t,f、ΔHf,n,t,f、ΔGm,n,t,f和Δpn,t,f分别为场景n中时段t的风电机组w的出力、电网节点i处的电负荷、热网节点f处的热负荷、气网节点m处的气负荷和电价的日前预测误差。

4）值函数

在动态规划框架下,通过递归求解Bellman 方程［32］,可以获得IES 的最优运行成本为:

式中:Vn,t(Sn,t)为在状态Sn,t下系统的最优总运行成本；E(⋅)为期望函数；Cn,t(Sn,t,xn,t)为由状态Sn,t执行决策xn,t而转移到状态Sn,t+1产生的瞬时成本；γ为范围从0 到1 的回报因子,γ=0,则值函数仅与当前时间的成本相关,γ越接近1,则值函数越多地考虑未来回报,使优化更具远见。

1.2 并行多维近似动态规划求解过程

PMADP 算法求解思想是利用状态变量聚合的方法,将状态变量以其灵活性资源丰富程度为依据进行筛选和聚合,利用值函数近似,解决“维数灾”的问题,利用状态空间压缩策略减小寻优范围,从而构造与并行计算相契合的PMADP 算法循环嵌套框架。

1.2.1 状态变量的聚合

引入决策后状态变量Sn,t,x表示做出决策后但随机因素的新信息还未到来之前的状态。通过采用Sn,t,x来避免式（8）中复杂的期望求解过程。基于此,式（8）可以表示为:

借助决策后值函数Vn,t,x(Sn,t,x)克服了随机因素对状态空间维数的影响。然而,在IES-SDED 问题求解中,高维连续状态变量使得Vn,t,x(Sn,t,x)的计算仍很困难,“维数灾”的问题依然存在。因此,本文提出以低维替代高维的状态空间聚合策略。状态变量聚合后的Bellman 方程为:

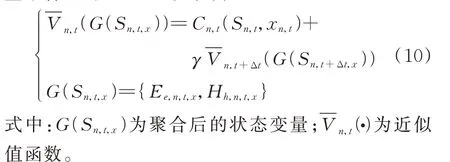
1.2.2 值函数的更新

本文建立由不同状态组合下的值函数组成的值表记录不同状态的值。若将ESS 的可用容量离散为E个状态,将HST 的可用热量离散为H个状态,则构建的值表大小为E×H×T。

每一次训练中,根据IES 每个时段t的当前状态及上一次训练所构建的值表进行决策,即

式中:arg min {⋅}为IES 所做出的最优决策；n为训练迭代次数。

在做出最优决策后,计算当前状态的样本估计值（如式（12）所示）,据此更新本次训练中的值函数,并记入值表。

式中:αn为0～1 之间的参数,通过调整αn的值,可以改变之前经验在本次值函数更新中的比重；v̂n,t为当前状态下的样本估计值。

1.2.3 状态空间的压缩

本文提出了仅保留有效状态的状态空间压缩策略,该策略利用ESS 和HST 的最大充放电/蓄放热限值约束将无效状态剔除,实现对状态空间的压缩。状态空间压缩思想,如附录B 图B1 所示。

由附录B 图B1 可见,第k′次迭代中时段t所解得第e个ESS 的可用容量和第h个HST 的可用热量的状态分别为Ee,t,k′和Hh,t,k′,将其设为当前状态,制定时段t+1 的最优决策,从而将状态分别转移到Ee,t+1,k′和Hh,t+1,k′。由ESS 运 行 约 束（附 录A 式（A15）和式（A16））及HST 的运行约束式（A22）和式（A23）可知,以状态Ee,t,k′和Hh,t,k′为起点可以转移得到的新状态Ee,t+1,k′和Hh,t+1,k′是有限的。基于此,将满足ESS 的最大充放电限值式（A15）和式（A16）、以 及HST 的 蓄 放 热 限 值 式（A22）和 式（A23）约束的状态定义为可到达的状态；否则定义为无法到达的状态,即无效状态,在计算中直接剔除,可有效降低求解规模,提高计算效率。

1.2.4 并行化

本文提出了将并行计算与多维近似动态规划（multi-dimensional approximate dynamic programming,MADP）相结合的PMADP 算法,以解决IES-SDED 问题中状态空间压缩后离线训练耗时长的问题。通过基于MADP 的IES-SDED 模型的并行计算可行性分析,将其描述为适用于并行求解的嵌套架构,并构建并行性能评价指标以衡量PMADP 算法的性能。

1）多维近似动态规划算法并行计算可行性分析

循环迭代任务可并行化的前提是该循环可以分解为若干个独立部分,即当前循环的执行不受之前循环结果的影响。基于该思想,构造IES-SDED 的3 层嵌套循环结构模型:最外层为训练次数循环；中间层为阶段变量循环,即对所有优化时段进行遍历循环；最内层为独立的状态变量循环,即对每个优化时段中的状态变量组合空间进行独立遍历循环。由此,本文模型架构与并行计算思想相契合,可采用并行计算的方式进行求解。

2）并行性能评价指标

为了验证并行求解策略的性能,本文以加速比SP和并行效率PE作为衡量并行计算性能的指标,表达式为:

式中:ts和tp分别为求解同一任务时的串行计算时间和并行计算时间；Pcore为参与并行计算的核心数。

若SP越接近于参与任务执行的核心数目,即PE越接近于1,则越能充分表征核心并行计算的参与度,并行计算的性能越高。

2 算例分析

本文以E6-H6-G6 测试系统和E118-H12-G12测试系统为例,验证本文所提IES-SDED 模型和PMADP 算法的有效性。E6-H6-G6 测试系统如附录B 图B2 所示,发电机和外网参数、气源参数、储能装置参数和日前预测信息（电价、电负荷、热负荷、气负荷和风电功率）见文献［33-34］。E118-H12-G12测试系统相关数据见文献［35］,采用MATLAB 软件调用CPLEX 求解器进行求解,计算机配置为Windows 10 系统,Intel Xeon E5-2678 CPU,主频为2.5 GHz,内存为64 GB。调度周期为24 h,每时段长度为1 h。

2.1 E6-H6-G6 算例

假设风电、电价以及负荷的预测误差均服从正态 分 布（ 即 ΔPw,n,t,f∼N(0,0.2), ΔDi,n,t,f∼N(0 ,0.05), ΔHf,n,t,f∼N(0,0.05), ΔGm,n,t,f∼N(0,0.05),Δpn,t,f∼N(0, 0.05)）,利用蒙特卡洛模拟 生 成10 000 组训练场景,对PMADP 算法进行充分训练,并用1 000 组测试场景来验证算法的准确性。

2.1.1 状态变量聚合策略灵活性比较

基于本文提出的状态变量聚合策略,以灵活性资源可调程度为依据,仅由灵活性能力高的状态变量组成状态空间,实现低维替代高维的目的。为了验证该聚合策略对IES-SDED 结果的影响,构建以下2 种场景:

1）场景1:不考虑状态变量聚合的贪心策略。

2）场景2:同时将状态变量聚合至ESS 可用容量和HST 可用热量。

其中,ESS 可用容量的离散间隔均设置为20 MW,HST 可用热量的离散间隔均设置为10 MW。

从1 000 组测试场景中随机抽取1 组分析场景1和场景2 中EPS、DHS、ESS 和HST 的调度决策,结果如图1 和图2 所示。图中,GT 为燃气轮机组,WT为风电机组。

图1 场景1 的调度决策结果Fig.1 Dispatch decision results in scenario 1

图2 场景2 的调度决策结果Fig.2 Dispatch decision results in scenario 2

1）场景1

由图1（a）和图1（c）可知,在调度初始时段（01:00―03:00）,ESS 完全释放,以实现每个独立调度时段经济性最优的目标。由于ESS 充放电行为只取决于当前调度寻优策略,该调度结果无法表征其对剩余独立调度周期的影响。因此,在低电价和电负荷低谷时段（14:00—17:00）,ESS 不充电；在高电价和电负荷高峰时段（11:00—13:00 和18:00—21:00）,ESS 不放电；而在18:00,由于ESS的可用容量已经耗尽,所以EPS 不得不以高价从外电网购电。在调度周期结束时刻,ESS 的可用容量无法回到初始状态,影响下一个周期调度策略的制定。

由图1（b）和图1（c）可知,在电负荷第1 个上升时段（从06:00 开始）,CHP 机组通过增加产电以满足电负荷需求,避免切负荷造成的高额惩罚成本。CHP 机组由此产生的多余热量被储存在HST中。由于HST 无法制定兼顾对未来影响的全局最优调度策略,在HST 拥有可调灵活性资源的时段（06:00―24:00）不放热。在调度周期结束时刻,HST 的可用热量无法回到初始状态,影响下一周期的调度。场景1 中ESS 和HST 的这种以单一独立调度时段经济性最优为目标的贪心调度策略无法充分发挥灵活性资源的柔性互补特性,无法得到全局最优决策。

2）场景2

由图2 可见,ESS 在高电价和电负荷高峰时段（08:00―13:00 和19:00―21:00）放电以满足电负荷需求；在低电价和电负荷低谷时段（01:00―02:00、04:00―05:00、14:00―17:00 和22:00―24:00）充电以避免弃风；HST 在电负荷低谷和热负荷高峰时段（01:00、04:00 和22:00―24:00）,以及电、热负荷低谷时段（14:00―16:00）放热以降低CHP 机组产电从而避免弃风；在电负荷高峰和热负荷低谷时段（11:00―13:00 和18:00―20:00）蓄热以储存CHP 机组为满足高电负荷而产生的多余热量。相较于场景1 的贪心策略,场景2 依据多能流耦合特点,综合考虑ESS 和HST 这2 种不同性质的灵活性存储设备,可充分发挥多能源荷之间的柔性互补优势,进而从全局的角度制定最优调度策略,避免由于灵活性资源挖掘不充分导致的弃风、高电价购电等风险。

2.1.2 状态变量离散策略对并行多维近似动态规划算法的影响

为了分析不同状态变量离散策略对PMADP 算法离线训练时间、在线调度时间、充分训练所需要的迭代次数以及单个不确定场景运行成本的影响,本文在场景2 的基础上,对ESS 的可用容量和HST 的可用热量选择不同的离散间隔以获得不同的状态空间离散策略,具体构建方案及结果比较如表1所示。

表1 不同状态变量离散策略对PMADP 算法的影响Table 1 Influence of discrete strategies of different state variables on PMADP algorithm

由表1 可知,随着ESS 和HST 的离散间隔减小,PMADP 算法离线训练时间、在线调度时间和迭代次数均呈明显的上升趋势。这是由于聚合后的状态空间中包含的状态数量与ESS 和HST 的离散间隔成反比,即离散间隔越小,状态空间中包含的状态数量越多。随着组成状态空间的状态数量的增加,PMADP 算法在每个时段都需要遍历更多的状态来获得全局最优的调度策略。因此,离线训练时间、在线调度时间和迭代次数均会明显增加。

随着ESS 和HST 离散间隔的减小,优化调度结果中运行成本整体呈下降趋势。在将ESS 和HST 分别以最小离散间隔10 MW 和5 MW 设置的E10-H5 离散策略下,PMADP 算法获得了最优的运行成本11 329 113.0 美元、最长离线训练时间1 930.8 s 和最长在线调度时间4.218 s；在E25-H25离散策略下,PMADP 算法获得了最差的运行成本11 383 869.6 美元、最短离线训练时间40.945 s 和最短在线调度时间1.07 s。由于PMADP 算法的优化复杂度与计算精度正相关,在实际的工程应用中,需要根据计算平台的性能及工程精度需求,在两者之间进行权衡。

2.1.3 状态空间压缩策略性能分析

本文从1 000 个测试场景中随机选取100 个训练场景验证压缩空间策略对提升计算效率的有效性。压缩前后的状态空间规模及计算时间比较结果如附录B 图B3 所示。

由附录B 图B3 可知,对所选取的100 个测试场景,采用本文提出的状态空间压缩策略后,在状态空间规模及计算时间方面均有大幅降低。平均状态空间规模降低了73.07%,平均求解时间降低了67.91%。这是因为本文提出的以储能装置运行约束为限值的状态空间压缩策略,可将不满足储能装置运行约束的状态剔除,通过对状态空间进行压缩,大大降低了求解规模,使求解效率得到有效提高。

2.1.4 并行多维近似动态规划收敛性验证

为验证本文所设置不确定性场景数量的合理性,从10 000 组不确定性场景中随机抽取4 000 组对采用E20-H10 离散策略的PMADP 算法进行训练,附录B 图B4 给出了运行成本的分布情况。

由附录B 图B4 可知,运行成本拟合曲线随迭代次数的增加呈下降趋势。当迭代次数达到3 000 次时,运行成本拟合曲线已基本达到平稳,可以认为PMADP 算法已经过充分训练,算法已经收敛。与确定性场景下的2 563 次迭代次数相比,算法收敛所需要的迭代次数增加了17.05%。因此,本文选取10 000 组训练场景以保证PAMDP 算法经过充分训练,保证了收敛性。

2.1.5 并行多维近似动态规划并行性能分析

本文采用加速比SP和计算效率PE这2 个评价指标衡量PMADP 算法在不同策略下求解IESSDED 问题的性能,不同状态变量离散策略下SP和PE随核心数的变化情况如附录B 图B5 所示。

由附录B 图B5 可知,在参与并行计算的CPU核心数相同的情况下,离散数目越多,SP越高,PE也越高。在离散数目相同的情况下,参与并行的CPU核心数越多,并行效率PE越低。这是由于CPU 内部各个核心在进行并行计算时需要通信和协调,随着参与并行计算的CPU 核心数的增加,核心之间的信息通信时间也会增加。然而,在处理大规模问题时,由于求解时间的增加,可忽略信息通信的时间。因此,在实际工程应用中,需要根据求解问题的计算规模合理选择CPU 核心数,以获得理想的SP和PE。

2.1.6 并行多维近似动态规划性能对比

不同算法下的运行成本期望值和总耗时如表2所示。

表2 E6-H6-G6 算例中3 种算法的计算结果Table 2 Calculation results of three algorithms in the case of E6-H6-G6

由表2 可知,在运行成本的期望值方面,SO 算法最低,为1 123 714.62 美元；MPC 算法最高,为1 144 954.7 美元,较SO 算法增加1.89%；本文所提PMADP 算 法 居 中,为1 128 131.24 美 元,较SO 算法仅增加0.83%。这是由于SO 算法对每个场景精确求解,进而获得了最低的成本期望值；而MPC 算法仅利用较短时间的不确定性预测值,制定的调度策略灵活性受限,故其成本期望值最高；本文所提PMADP 算法充分利用全局不确定性信息,解决了MPC 算法的灵活性受限问题。在总调度时间方面,本文所提出的PMADP 算法由于利用并行化求解思想充分调用求解资源,在3 种算法中耗时最短,为4 551 s,较MPC 算法加快了53.80%,较SO 算法加快了82.77%。可见,本文所提PMADP 算法虽然在计算精度方面略低于SO 算法,但在计算效率上具有显著优势。因此,在处理对计算时间有着较高要求的IES-SDED 问题时,利用本文所提PMADP 算法求解可以获得理想的效果。

2.2 E118-H12-G12 算例

为进一步验证本文所提PMADP 算法在求解计及多元不确定性的大规模复杂系统时的适应性,本文分别将PMADP 算法、MPC 算法及传统的串行MADP 算法应用于E118-H12-G12 测试系统的IESSDED 问题求解中,对比其计算精度及计算效率。

本文所采用的E118-H12-G12 测试系统考虑2台ESS 和2 台HST,EPS、DHS 及NGS 的 其 他 数 据设置参考文献［34］。本算例设定的离线训练场景和在线测试场景同E6-H6-G6 算例。

2.2.1 运行成本及计算时间对比

3 种算法求解计及多元不确定性的IES-SDED问题的运行成本期望值及单个测试场景计算时间如表3 所示。

表3 E118-H12-G12 算例中3 种算法的计算结果Table 3 Calculation results of three algorithms in the case of E118-H12-G12

由表3 可知,运行成本的期望值方面,本文所提PMADP 算法为4 150 742.27 美元,相较于MPC 算法降低了8.27%,体现出明显的计算精度优势；计算时间方面,本文所提PMADP 算法为152.251 s,较MPC 算法和MADP 算法分别减少了79.93% 和53.09%。传统的串行MADP 算法虽然获得了与PMADP 算法相同的运行成本期望值,但过低的计算效率使其难以应用于大规模复杂系统的求解。因此,从整体最优角度,本文所提PMADP 算法在对大规模复杂系统求解时仍能在计算精度和计算效率上均保持显著的优越性。

2.2.2 状态变量离散策略对并行多维近似动态规划算法影响分析

在大规模复杂系统IES-SDED 问题的求解中,大量储能装置计入状态空间对状态变量离散策略的合理制定提出了更高的要求,附录B 图B6 为不同状态变量离散策略下本文所提PMADP 算法和传统MADP 算法在计算时间方面的比较结果,以及PMADP 算法对计算效率的提升趋势。

由附录B 图B6 可知,随着ESS 和HST 的离散间隔减小即状态空间增大,MADP 算法和PMADP算法的计算时间均有明显增加。由图B6（d）可知,2 种算法的计算时间增加率有着明显的不同。随着状态空间的增大,本文所提出的PMADP 算法的计算时间增加平缓,而传统MADP 算法的计算时间呈指数级上升。这是由于随着状态空间的增大,每个时段都需要遍历更多的状态来获得全局最优的调度策略,求解复杂度急剧升高。本文所提PMADP 算法较传统串行MADP 算法可以更充分地利用多核CPU 的计算资源,将规模庞大的复杂问题拆分为多个简单问题并行求解,大大减少了计算时间。随着计算复杂程度及问题规模的增大,CPU 核心内部信息交换时间可以被忽略,本文所提PMADP 算法能充分挖掘CPU 的多核并行计算资源,效率提升更加明显,从而发挥出其在大规模问题求解上的优越性。

3 结语

本文提出了一种可以快速求解IES-SDED 问题的PMADP 算法,通过算例分析,得出以下结论:

1）提出的低维替代高维的状态变量聚合机制,与传统ADP 算法相比,有效降低了状态空间的维数,克服了“维数灾”的问题,提高了求解效率。

2）提出的基于储能运行限值的状态空间压缩策略,通过剔除不可行状态,避免了对整个状态空间的穷举计算,状态空间规模可降低70%以上,求解时间可减少60%以上,进一步提高了求解效率。

3）在确定性和不确定性场景下,相比于其他算法,本文所提出的PMADP 算法能更好地兼顾计算精度和计算效率,对大规模复杂系统也具有较好的适用性。

未来工作将深入研究PMADP 算法效率提升方法和求解计及大规模储能装置IES-SDED 问题的适用性,进一步提高PMADP 算法在实际工程中的应用范围。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。