电化学极化状态对潜艇螺旋桨扰动电场模型的影响*

何 芳，王向军

(海军工程大学 电气工程学院， 湖北 武汉 430033)

潜艇全寿命服役期间，刚下水期、航行期、进坞小修期每个阶段的潜艇腐蚀静电场特征差异明显，潜艇腐蚀静电场与船体材料的电化学极化状态有关。船体涂层退化程度不同，材料的电化学极化状态会发生改变。当涂层性能开始下降时，由于海水电阻导电性能远优于潜艇轴电阻，轴电阻上可近似为无电流导通，船体与螺旋桨内部之间可视为电气绝缘，宏观上看船体与螺旋桨为两个独立的异种金属，在海水中各自发生腐蚀，此时材料极化过电位可忽略。涂层经过海水长期浸泡后，即使涂层无破损、金属无裸露部分，海水也仍可以透过涂层腐蚀船体。对高电阻离子导体膜涂层而言，此时的极化状态可以看作线性极化。若涂层局部已发生破损，船壳会通过涂层局部破损处与铜制螺旋桨在海水中直接构成腐蚀电偶，此时材料电化学极化状态可视为非线性极化，即选取船体与螺旋桨材料极化曲线的非线性区间。本文按照潜艇刚下水期、航行期、进坞小修期的三个服役阶段，将涂层状态定性划分成涂层性能下降、涂层渗透腐蚀、涂层局部破损三种情况，分别以恒电位、线性极化、非线性极化三种极化状态为边界条件，建立服役期间不同阶段的潜艇腐蚀静电场模型，并研究不同边界条件对螺旋桨扰动电场的影响。

1 基于边界元法的螺旋桨扰动电场模型

潜艇水下静电场可视为无源场，满足拉普拉斯方程，见式(1)。电磁场边值条件一般分为三类：边界电位已知的第一类边值条件(狄立克雷边值条件)，如各种金属置于海水中的自腐蚀电位[1-4]；电流密度已知的第二类边值条件(诺依曼边值条件)，如阴极保护系统中的阳极输出电流[5-9]；边界电位和电流密度函数已知的第三类边值(混合边值条件)，如阳极、阴极表面的极化曲线函数[10-12]。这三种边值条件对应的函数描述如式(2)。基于边界元法的潜艇腐蚀静电场建模中的边值问题，通常考虑以材料极化状态为边界条件，主要有三种处理方法：一是不考虑极化过电位，采用恒电位边界；二是将极化电位与电流密度视为线性关系，以极化曲线的线性区间作为边界；三是采用材料的非线性极化曲线为边界，引入电极电位或过电位随电流密度变化的函数关系。

(1)

(2)

螺旋桨旋转时会在螺旋桨区域附近形成扰动电场，扰动电场的建模思想是：将螺旋桨近区的连续电场源离散化成为分布于旋转轨迹上的有限个固定点电源，利用离散化处理后的点电场源，采用边界元法分别计算单个旋转点电源的电场，再进行多个旋转点电源电场叠加。取一有限长圆柱体作为螺旋桨近区边界面，将其边界面离散，如图1所示，将螺旋桨桨叶等效成点电荷，计算旋转点电荷在边界面上的离散电位，代入边界元方程组式(3)，即可推算水下螺旋桨扰动电场。

图1 螺旋桨边界面离散及等效电荷Fig.1 Boundary interface and discrete and equivalent charge graph of propeller

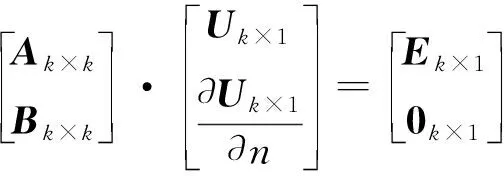
(3)

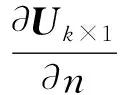
2 螺旋桨扰动电场仿真

利用COMSOL多物理耦合场软件[13]仿真时，采用二次电流分布场。仿真对象为某型潜艇，长75 m、宽6 m、高7.5 m，按实艇比例建立模型，以平行于潜艇纵向方向由舰艉向舰艏为X轴正方向，以平行于潜艇横向方向由左舷向右舷为Y轴正方向，以垂直于水面指向天空方向为Z轴正方向，笛卡尔坐标系原点位于潜艇几何中心处，如图2所示。

图2 潜艇模型及坐标Fig.2 Submarine model and coordinate diagram

针对不同边界条件建立涂层性能下降、浸泡于海水涂层渗透腐蚀、涂层局部破损极化模型，恒电位边界为常数，线性极化边界采用式(4)，非线性极化边界采用式(5)[14]。式(4)、式(5)中J为极化电流密度，j0为电极体系的腐蚀电流密度，E为极化电位，E0为平衡电位，Rp为线性极化电阻，ba、bc为阳极、阴极Tafel斜率。恒电位边界、线性极化边界及非线性极化边界电化学参数由电化学工作站CorrTest仪器三电极体系[15]测定。测定921合金钢材料、镍青铜材料的自腐蚀电位参数见表1。测定船用921合金钢材料、镍青铜材料的线性极化曲线，采用动电位扫描法，扫描速度30 mV/min，线性极化曲线如图3(a)所示，CorrView软件拟合线性极化曲线，计算腐蚀电流密度和线性极化电阻[16]见表1。测定船用921合金钢材料、螺旋桨镍青铜材料非线性极化曲线，采用电位扫描法，用20～60 mV/min的电位扫描速度进行测量，测定结果如图3(b)所示，对非极化曲线采用CorrView软件进行最小二乘拟合[16]，拟合后的阳极、阴极Tafel 斜率见表1。

(4)

(5)

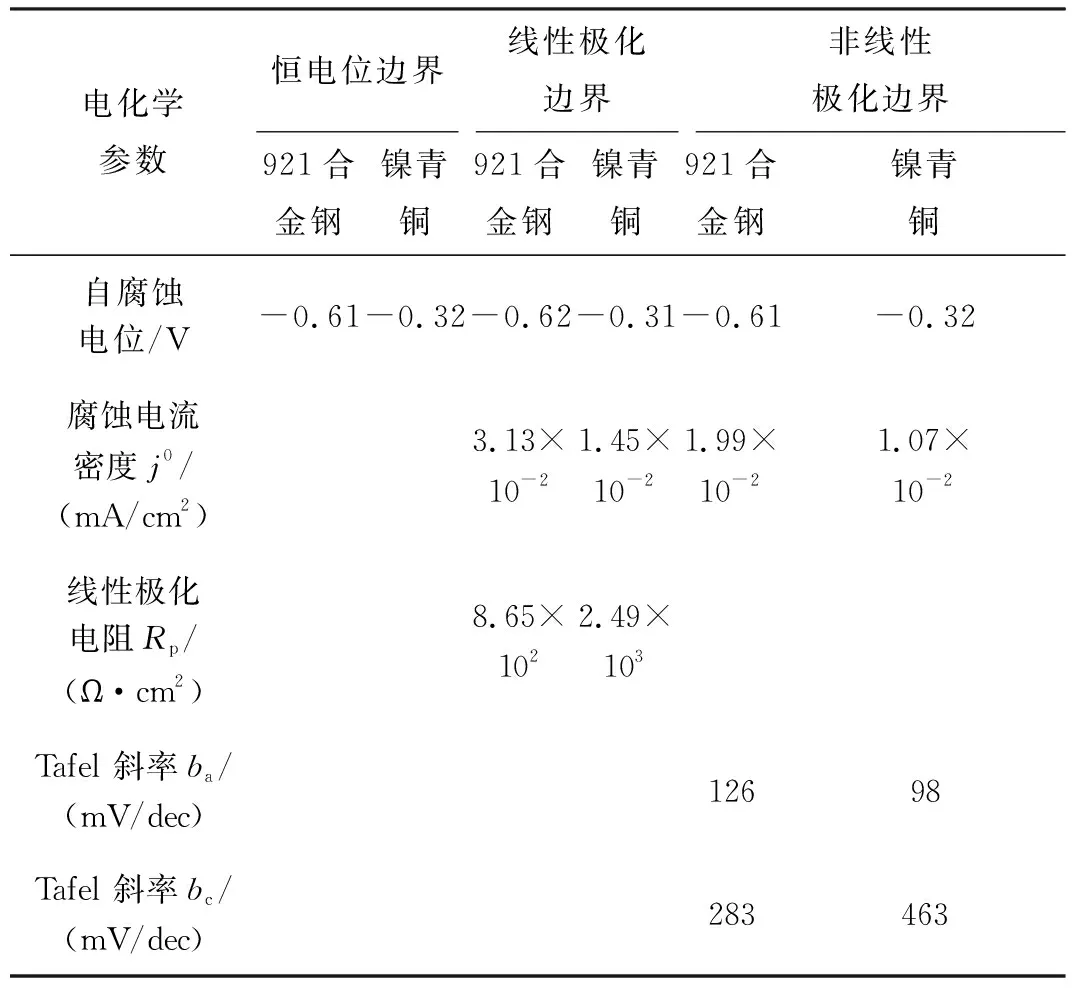
表1 三种边界条件的电化学参数Tab.1 Electrochemical parameters under three boundary conditions

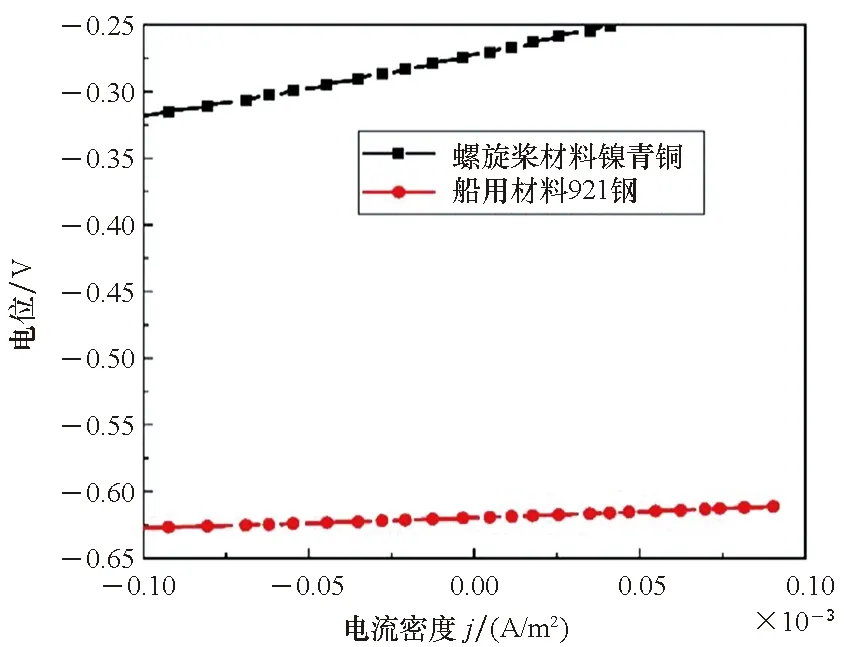
(a) 材料线性极化曲线(a) Liner polarization curve of the material

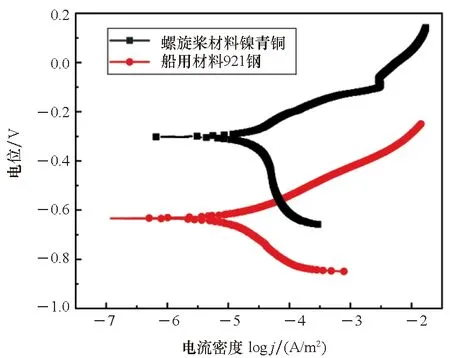
(b) 材料非线性极化曲线(b) Nonlinear polarization curve of the material图3 船用材料极化曲线测定Fig.3 Polarization curve of submarine materials

潜艇模型螺旋桨为5叶桨，旋转角频率为3.14 rad/s，频率为0.5 Hz，在固定点观测相当于1 s时间内变化2.5次，相当于固定观测点处的螺旋桨旋转频率为2.5 Hz，选取螺旋桨旋转近场区观测坐标点(-39.7,1.8,0) m，对比不同边界条件下螺旋桨旋转对潜艇腐蚀静电场的扰动影响。

3 仿真结果与讨论

3.1 涂层性能下降模型

涂层性能下降情况，采用恒电位边界，电场三分量基本呈正弦变化，变化频率与螺旋桨旋转频率一致。5片桨叶划过在观测点(-39.7,1.8,0) m处横向和纵向电场分量波峰处会出现明显的5次小峰瓣，垂直向电场分量从波峰至波谷处5次峰瓣呈变形趋势下降，电场三分量如图4(a)、(b)、(c)所示。电场模值以正弦规律变化，变化频率与螺旋桨旋转频率相同，峰瓣数为螺旋桨桨叶数，特征非常明显，原始扰动信号电场模峰峰值约为7 mV/m。对扰动信号电场模值进行分频处理，3 Hz低通滤波后为峰波平滑的正弦波，30 Hz高通滤波后的信号无明显周期特征，如图5所示。

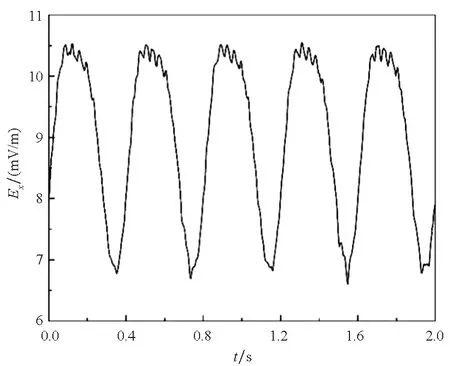
(a) Ex

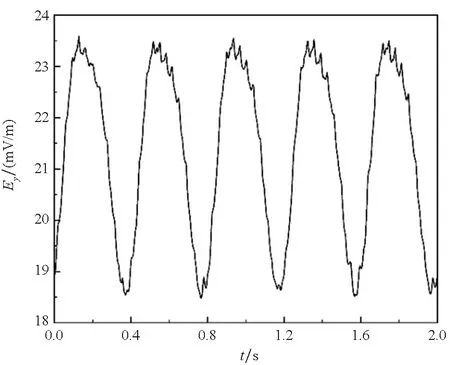
(b) Ey

(c) Ez图4 恒电位边界下静电场扰动Fig.4 Disturbance of electrostatic field under constant potential boundary

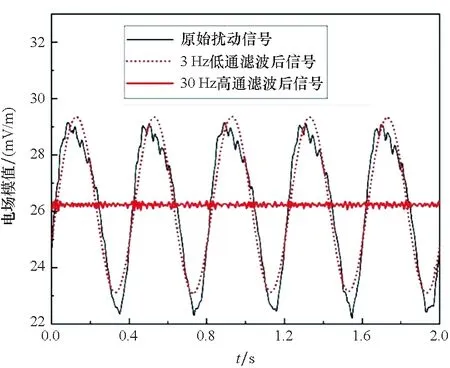
图5 恒电位边界下扰动信号分频滤波后电场模值Fig.5 Electric field modulus of frequency division disturbance signal under constant potential boundary

原始扰动信号、3 Hz低通和30 Hz高通滤波分频信号电位波形如图6所示。原始扰动信号电位峰峰值约为2.6 mV，波峰处可见峰瓣变化，但因谐波范围较小，峰瓣数目不明显；3 Hz低通滤波滤掉了信号的高次扰动频率，只剩下基频信号，呈现波峰平滑的正弦波，频率为2.5 Hz；30 Hz高通滤波后的电位信号无明显周期特征。

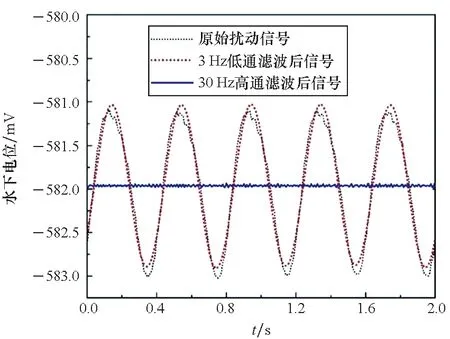
图6 恒电位边界下扰动信号分频滤波后电位Fig.6 Potential of frequency division disturbance signal under constant potential boundary

3.2 涂层渗透腐蚀模型

浸泡于海水的涂层渗透腐蚀情况，采用线性极化边界，电场三分量呈现与螺旋桨旋转频率一致的周期信号变化。电场横向分量Ex和垂直分量Ez可见多次谐波叠加，电场纵向分量Ey从波谷至波峰处峰瓣变化明显，谐波叠加后峰瓣数目不明显，如图7(a)、(b)、(c)所示。

(a) Ex

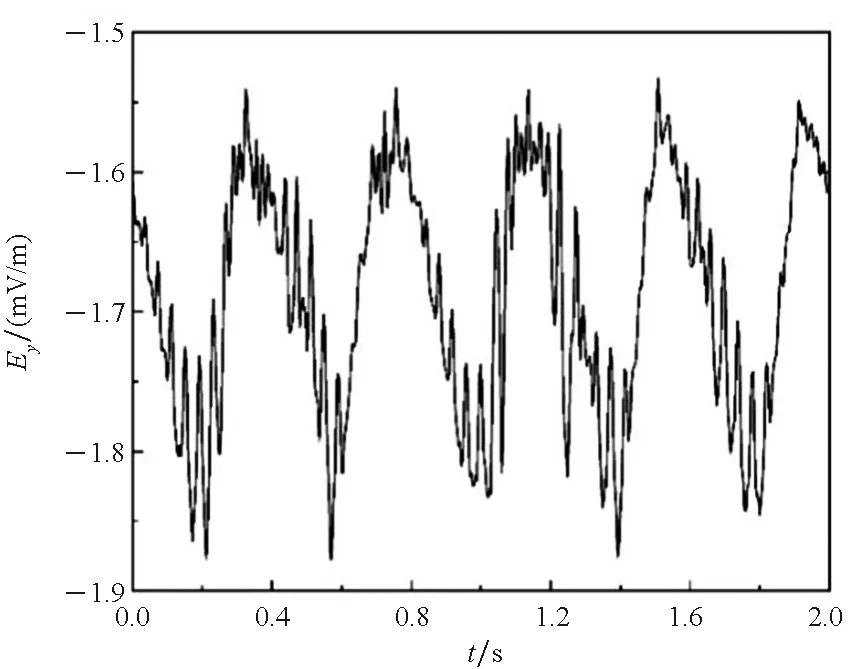
(b) Ey

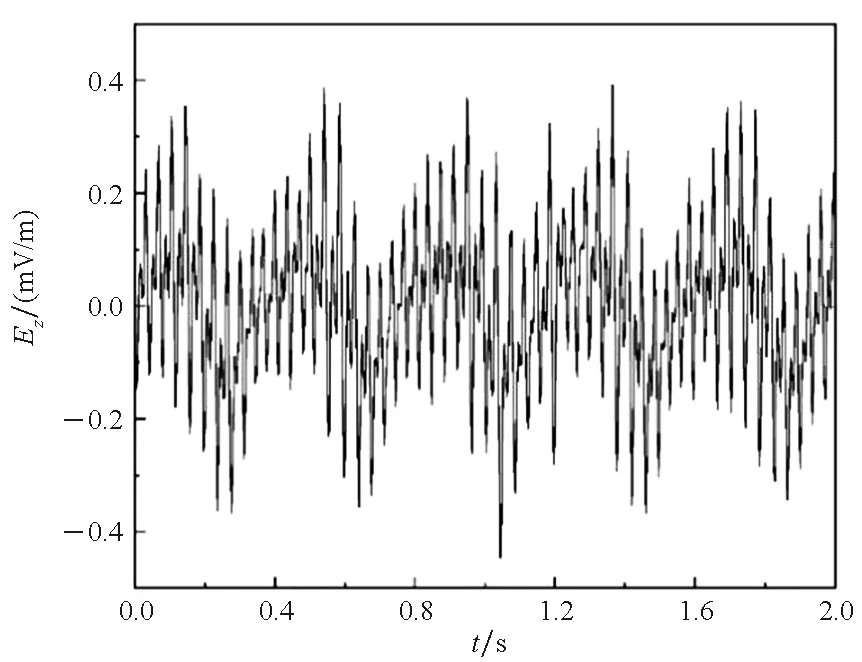
(c) Ez图7 线性极化边界下静电场扰动Fig.7 Disturbance of electrostatic field under linear polarization boundary

电场模值呈现与螺旋桨旋转频率一致的周期信号变化，多次谐波叠加特征明显，因谐波范围相对恒电位边界更广泛，谐波叠加后看不到明显的峰瓣，原始扰动信号电场模峰峰值约为0.6 mV/m。对扰动信号电场模值进行分频处理，3 Hz低通、10 Hz低通、50 Hz高通、100 Hz高通滤波后的信号电场模值见图8(a)、(b)，50 Hz以上信号电场模值已无明显周期特征。

(a) 分频滤波后低频信号(a) Low frequency signal after crossover filtering

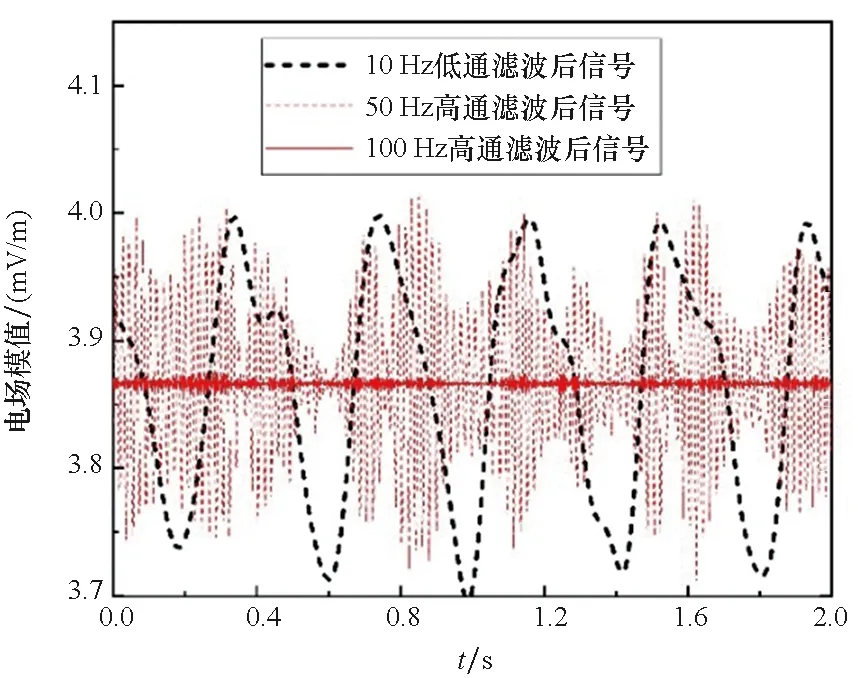
(b) 分频滤波后高频信号(b) High frequency signal after crossover filtering图8 线性极化边界下扰动信号分频滤波后电场模值Fig.8 Electric field modulus of frequency division disturbance signal under linear polarization boundary

原始扰动信号、3 Hz低通、30 Hz高通分频滤波后信号电位如图9所示。原始扰动信号电位峰峰值约为0.08 mV，波峰处峰瓣规律明显，波峰至波谷可见明显波瓣，线性边界扰动频率和2倍扰动频率占比相差较小，扰动频率电位和2倍扰动频率电位叠加效果后波峰明显；3 Hz低通滤波滤掉了信号的高次扰动频率，只剩下基频信号，呈现规则的频率为2.5 Hz的正弦波；30 Hz高通滤波后仍可见规律的周期信号。

图9 线性极化边界下分频滤波后信号电位Fig.9 Potential of frequency division disturbance signal under linear polarization boundary

3.3 涂层局部破损极化模型

涂层局部破损极化情况，采用非线性极化边界，电场三分量呈现与螺旋桨旋转频率一致的周期信号变化。电场横向分量Ex和垂直分量Ez可见明显的多次谐波叠加，电场纵向分量Ey从波谷至波峰处峰瓣变化明显，谐波叠加后峰瓣数目不明显，如图10(a)、(b)、(c)所示。电场模值呈现与螺旋桨旋转频率一致的周期信号变化，多次谐波叠加特征明显，谐波范围相比于恒电位、线性边界要广，谐波叠加后峰瓣不明显，原始扰动信号电场模峰峰值约为6 mV/m。

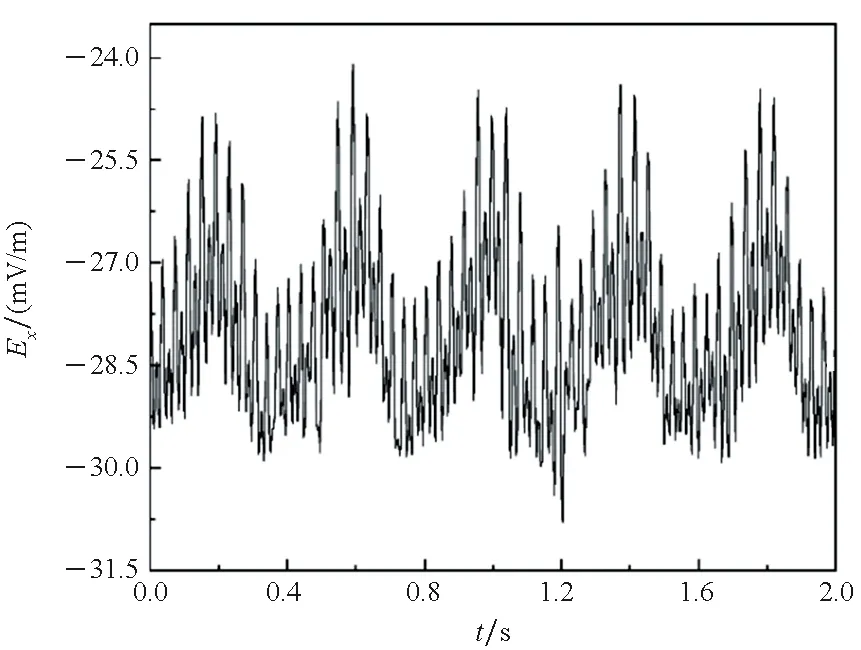
(a) Ex

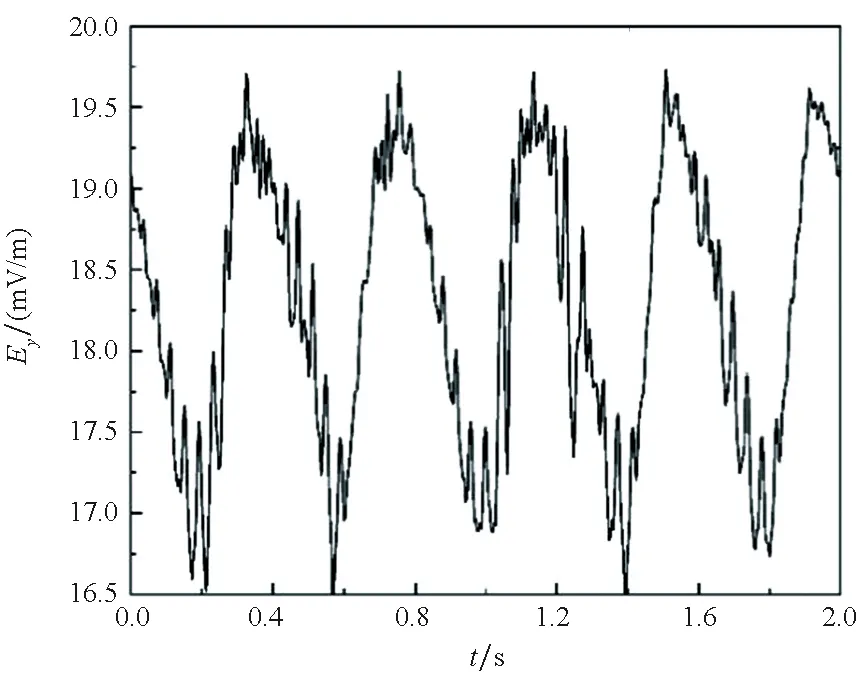
(b) Ey

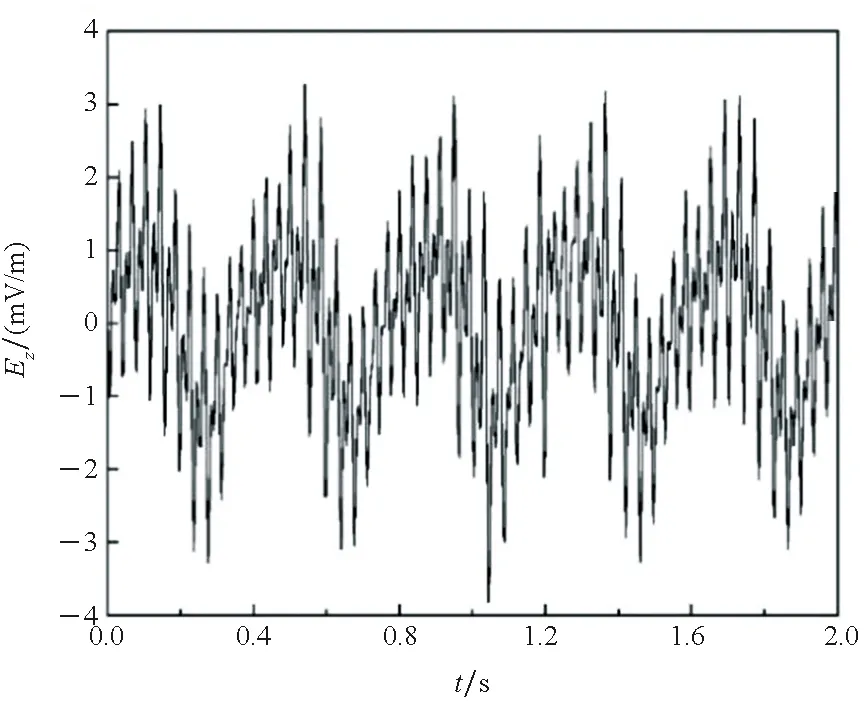
(c) Ez图10 非线性极化边界下静电场扰动Fig.10 Electrostatic field disturbance under nonlinear polarization boundary

对扰动信号电场模值进行分频处理，3 Hz低通、10 Hz低通、50 Hz高通、100 Hz高通滤波后的信号如图11所示，50 Hz分频后仍可见周期特征信号，100 Hz以上信号无明显周期特征。原始扰动电位信号、3 Hz低通、30 Hz高通分频滤波后电位信号如图12所示，原始扰动信号电位峰峰值约为0.9 mV，波峰处峰瓣规律明显，波峰至波谷也可见明显波瓣，原因在于非线性边界扰动频率和2倍扰动频率的幅值占比相对恒电位边界和线性边界而言最大，所以扰动频率电位和2倍扰动频率电位叠加效果后波峰明显。3 Hz低通滤波滤掉了信号的高次扰动频率，只剩下基频信号，呈现规则的频率为2.5 Hz的正弦波，30 Hz高通滤波后仍可见规律的周期信号。

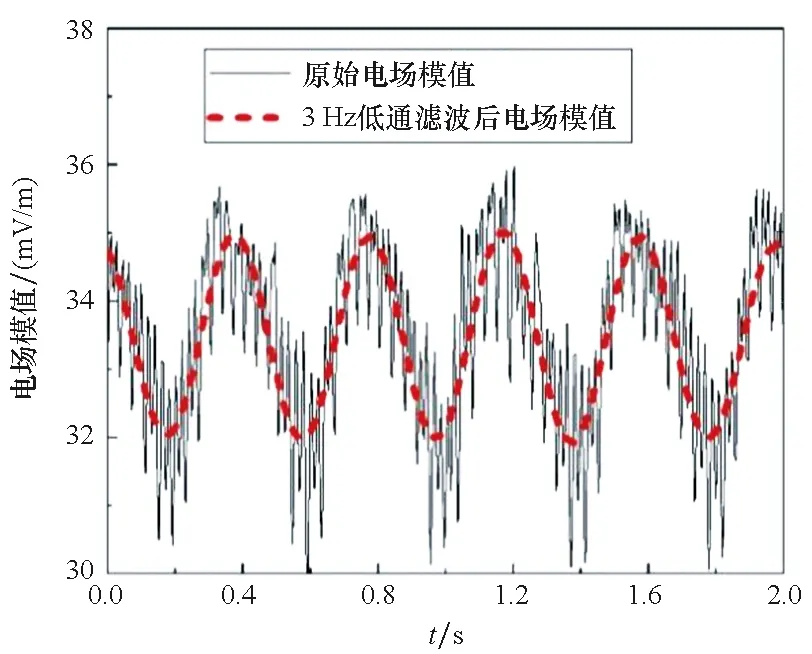
(a) 分频滤波后低频信号(a) Low frequency signal after crossover filtering

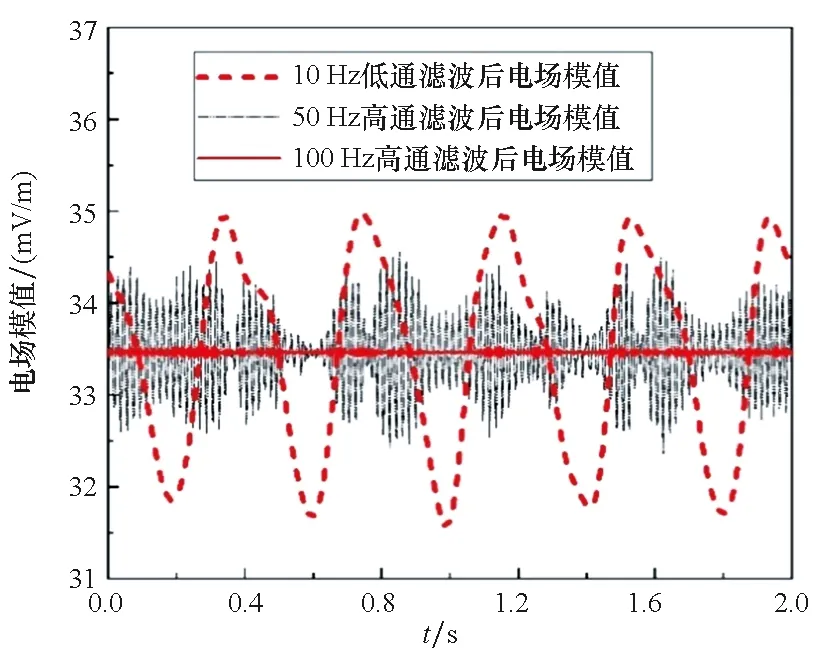
(b) 分频滤波后高频信号(b) High frequency signal after crossover filtering图11 非线性极化边界下扰动信号分频滤波后电场模值Fig.11 Electric field modulus of frequency division disturbance signal under nonlinear polarization boundary

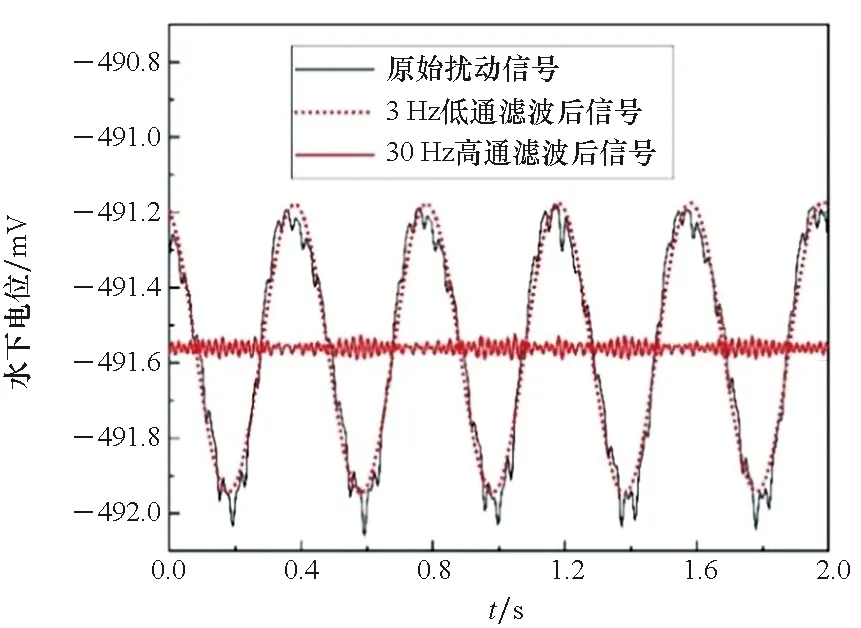
图12 非线性极化边界下扰动信号分频滤波后电位Fig.12 Potential of frequency division disturbance signal under nonlinear polarization boundary

3.4 三种模型水下电场信号特征对比

对比涂层性能下降、浸泡于海水涂层渗透腐蚀、涂层局部破损极化情况下的三种模型电场幅值及谐波范围，如图13、图14所示。为分析三种模型电场模值的幅频成分，以平行于横坐标为水平线，每种模型中的直流成分和扰动频成分的柱状顶端连线，与水平线之间的夹角作为观察角θ。以相同频率旋转扰动静电场，三种边界条件下的电场模型幅频特性中，直流成分比重最大，其他各频率成分占比与观察角θ有关。当θ较大时，各频率成分占比相差较大；反之θ较小时，各频率成分占比相差较小。恒电位边界下θ1=45°，线性边界条件下θ2=30°，非线性边界条件下θ3=60°，如图13所示。非线性边界条件下扰动频率2.5 Hz和2倍扰动频5 Hz占比相差最大，线性边界条件下扰动频率2.5 Hz和2倍扰动频5 Hz占比相差最小。3倍扰动频以上频段三种边界条件下模型会出现谐波范围的改变，恒电位边界下模型谐波范围较小，非线性边界下模型谐波范围最大，如图14所示，图中45～55 Hz区间放大对比可以清楚地看到非线性边界和线性边界下的谐波范围。

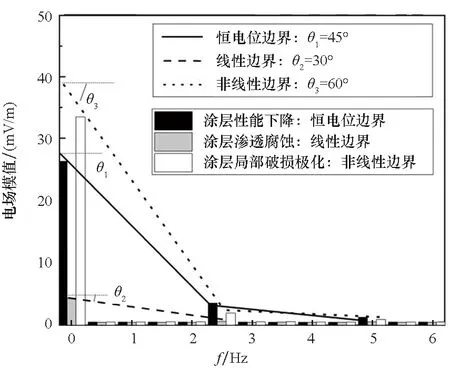
图13 不同边界条件下扰动信号幅频成分对比Fig.13 Comparison of amplitude frequency components of disturbance signals under different boundary conditions

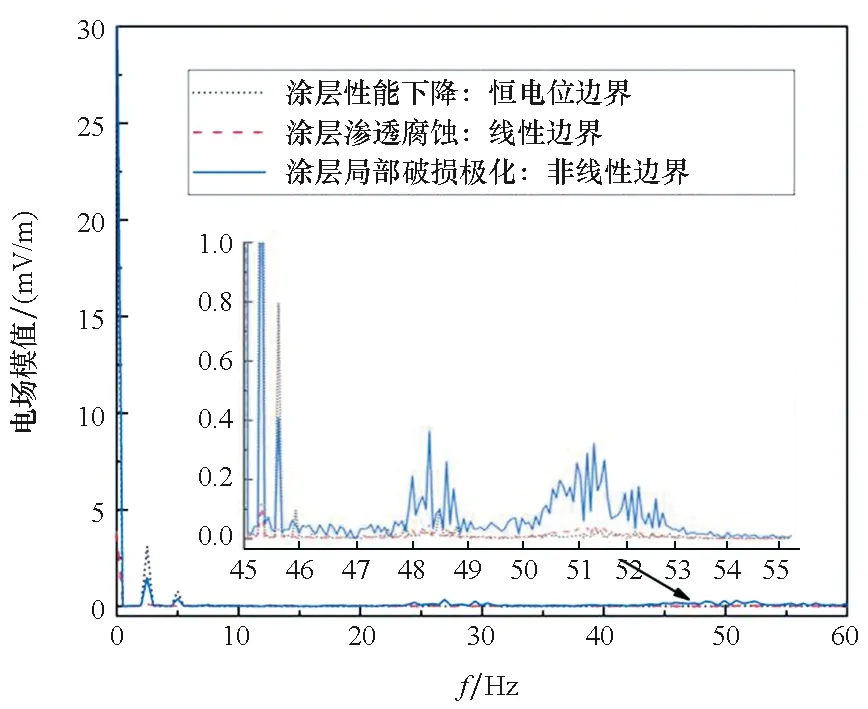
图14 不同边界条件下扰动信号谐波范围对比Fig.14 Comparison of harmonic range of disturbance signal under different boundary conditions

恒电位边界条件下的电场模型50 Hz以上谐波振幅趋近于0，线性边界和非线性边界条件下模型谐波范围明显；100 Hz以上非线性边界模型谐波仍然很明显。为对比不同电场模型的信号特性，以3 Hz、10 Hz、50 Hz、100 Hz作为分频点进行分频滤波分析。

在坐标(-39.7,1.8,0) m处螺旋桨扰动下，不同电场模型的静电场三分量峰峰值及电位峰峰值对比如表2所示。扰动仅在螺旋桨附近形成，涂层性能下降电场模型谐波范围为0～50 Hz、涂层渗透腐蚀静电场模型谐波范围为0～100 Hz，涂层局部破损极化模型谐波范围可达100 Hz以上。对比三种电场模型，最大电场分量峰峰值仅7 mV/m，最大电位峰峰值不超过3 mV，远离场源处电场和电位并未受到扰动影响，相对而言，螺旋桨旋转带来的电位及电场扰动在远场区域完全可以忽略。

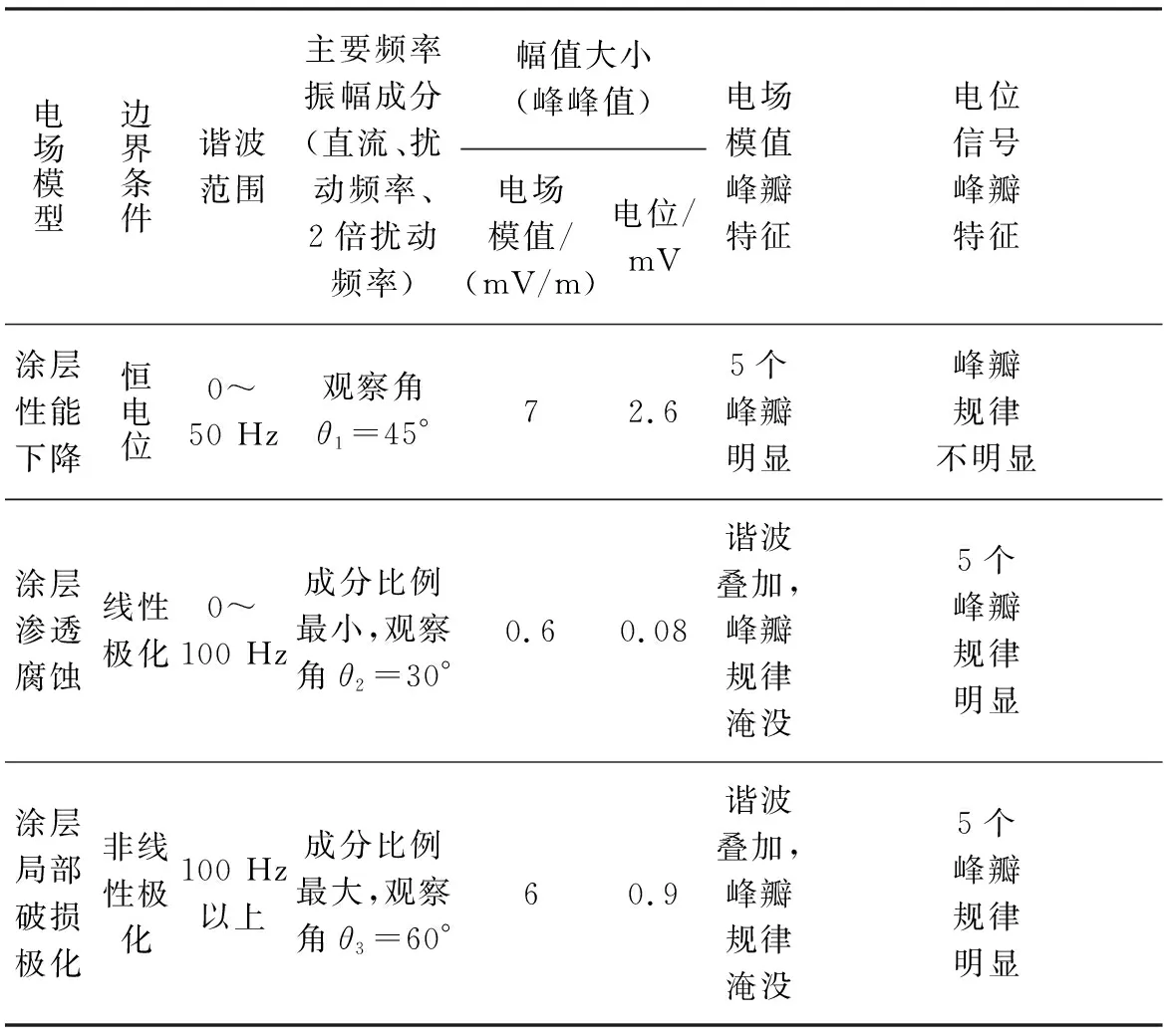
表2 不同边界条件对静电场的扰动影响Tab.2 Influence on electrostatic field disturbance under different boundary conditions

4 结论

以潜艇材料不同时期的电化学极化状态为边界条件，建立了舰船服役期间潜艇涂层性能下降、涂层渗透腐蚀、涂层局部破损极化三种腐蚀静电场模型，并从电位的时域信号特征及电场谐波频域特征对比分析了恒电位、线性边界、非线性边界对螺旋桨扰动电场模型的影响：

1)以恒电位作边界条件时，电位信号峰瓣特征不明显，但电场模值峰瓣规律明显；线性边界、非线性边界电位信号峰瓣规律明显，电场信号由于谐波叠加，电场模值峰瓣规律被淹没。

2)不同边界条件下，螺旋桨以相同频率旋转扰动静电场，直流占主要成分，其他频率成分占比与观察角相关。非线性边界条件下扰动频率和2倍扰动频占比相差最大，线性边界条件下扰动频率和2倍扰动频占比相差最小。

3)三种边界条件下电场模型的3倍扰动频以上频段谐波范围会发生改变，恒电位边界下模型谐波范围最小，非线性边界条件下谐波范围最大。