OFDM-MIMO雷达转发式主瓣干扰自适应抑制方法*

熊智敏，王党卫，李星辉

(1. 国防科技大学 信息通信学院, 湖北 武汉 430010； 2. 空军预警学院 预警技术系, 湖北 武汉 430019)

转发式干扰是实现对现代雷达有效干扰的重要干扰样式，其主要通过射频存储技术将接收到的雷达信号时延，实现不同的距离偏移，并经雷达主瓣接收后在距离维产生强的假目标，淹没真实目标，进而严重影响雷达对目标的探测能力。转发式干扰本质上是雷达发射信号的回转，雷达波束主瓣接收后，与真实目标回波混叠，常规的空域滤波和频域滤波技术基本失效，对其有效抑制一直是雷达干扰抑制的难题[1-4]。

通过发射正交频率分集调频(orthogonal frequency division modulated，OFDM)信号，实现距离依赖波束是频率分集多输入多输出(multiple input multiple output, MIMO)雷达研究的新方向,受到众多学者的深入研究[5-9]。与传统相控阵雷达不同，频率分集MIMO雷达相邻阵元发射信号通过引入一定频率间隔，使得形成波束具有距离-角度耦合性，可在距离-空间两维实现滤波[7]。利用这一特性，2015年，Xu等提出了一种基于自适应距离-角度二维波束形成的转发式干扰抑制方法，通过将波束指向相同角度、不同距离的单元上，使其具有抑制主瓣转发式干扰的能力[10]；同年，Gao等基于相似的原理，实现了空间相同角度、不同距离干扰的抑制[11]。更进一步，2017年，Li等则提出了基于自适应检测的转发式干扰抑制方法[12]。尽管上述两类方法为转发式干扰抑制提供了新思路，但基于自适应波束形成的抑制方法性能受限于阵列阵元数，且波束形状的控制更为困难；而自适应检测方法则因外部圆锥集的制约，检测器难以实现最优检测，即存在信噪比损失问题。

空时自适应处理(space time adaptive processing, STAP)技术是一种利用多个空域通道信息和相干脉冲串提供的时域信息在空间-时间二维自适应滤波的方法，能有效提升多通道雷达杂波抑制性能[13]。近年来，Xu和王委等分别研究了频率分集MIMO雷达通过STAP抑制距离模糊杂波和STAP实现问题，促进了频率分集MIMO雷达STAP的发展[14-15]。尽管，利用STAP的频率分集MIMO雷达转发式主瓣干扰抑制还未见报道，但STAP所采用的空间-时间二维联合处理思想为在距离维抑制转发式主瓣干扰提供了新思路[16-17]。

基于上述认识，本文首先探讨了OFDM-MIMO雷达转发式干扰回波模型，对最小方差无失真响应(minimun variance distortionless response,MVDR)在传统相控阵、经典MIMO以及OFDM-MIMO雷达中的应用进行探究，然后提出了自适应处理算法对OFDM-MIMO雷达转发式干扰进行抑制，并与传统算法进行对比。

1 OFDM-MIMO雷达转发式干扰回波模型

为方便分析，设OFDM-MIMO雷达采用N个阵元的均匀线阵，阵元间距为d，第n个阵元发射信号载频fn=f0+(n-1)B，其中f0为初始载频，B为各发射阵元的信号带宽，定义各发射阵元信号载频之间频差为Δf，则第n个阵元发射信号可表示为

sn(t)=u(t)exp(j2πfnt)

(1)

式中，复包络u(t)可表示为

(2)

Ts为脉冲宽度，μ=B/Ts为调频率。

同时，建立如图1所示几何观测模型，设定第一个阵元为参考阵元，干扰源与阵列法线方向夹角为θj，其到第一个阵元的径向距离为rj，则干扰机截获的信号可以表示为

图1 几何观测模型Fig.1 Geometric observation model

(3)

式中，τj=rj/c为参考阵元至干扰源的时延，τj,n=(n-1)dsinθj/c为参考阵元与第n个阵元间时延，c为电磁波传播速度。

现代雷达常为脉冲体制[18]，若设干扰机存储并在下一脉冲到来前转发截获信号，其转发时调制附加的延时和速度，为了方便表述，将转发调制的时延与τj合并考虑，调制速度记为vj(可取正值或负值)；目标雷达散射截面(radar cross section,RCS)为σ，与阵列法线方向夹角为θ，距离参考阵元径向距离为r，径向速度为Vr(可取正值或负值)，则由文献[14]转发式干扰模型可知，OFDM-MIMO雷达第m个阵元接收的第k个脉冲回波信号可表示为

exp[j2πfn(t-2τT,k-τT,n-τT,m)]+

exp[j2πfn(t-2τj,k-τj,n-τj,m)]+vkm(t)

(4)

式中：τT,k=[r-(k-1)VrTr]/c，Tr表示脉冲重复周期；τT,n=(n-1)dsinθ/c；τT,m=(m-1)dsinθ/c；τj,k=[rj-(k-1)vjTr]；τj,m=(m-1)dsinθj/c；ρ为转发式干扰调制幅度；vkm(t)为接收机噪声。

更进一步，经过下变频和脉冲压缩处理后，第m个阵元第n个接收通道的基带信号可表示为

yk,mn(t)=αsinc[B(t-2τT,k-τT,n-τT,m)]·

exp[-j2πfn(2τT,k+τT,n+τT,m)]+

βsinc[B(t-2τj,k-τj,n-τj,m)]·

exp[-j2πfn(2τj,k+τj,n+τj,m)]+

v′k,mn(t)

(5)

式中，α和β分别为脉压后目标回波和干扰信号，v′k,mn(t)为脉压后噪声。

一般来说，干扰进入目标主瓣时，此时τj,k≠τT,k，而窄带雷达阵元间位置差异对距离主瓣的影响可忽略，因此，若设λ为f0对应的波长，ρr=c/(2B)为距离分辨率，则当|fdTr|≪ρr时，接收通道基带信号yk,mn(t)为

yk,mn(t)≈α′k,nsinc[B(t-2τT,k)]·

exp[-j2πfn(τT,n+τT,m)]+

β′k,nsinc[B(t-2τj,k)]·

exp[-j2πfn(τj,n+τj,m)]+v′k,mn(t)

(6)

式中，

其中α′=αexp(-j4πr/λ)，β′=βexp(-j4πrj/λ)，且fd=2Vr/λ，f′d=2vj/λ。

更进一步，若令ΦT,mn=2πfn(τT,n+τT,m)，Φj,mn=2πfn(τj,n+τj,m)且d≪ρr时，则可得

(9)

于是，对于整个接收阵列，经A/D采样后，对于第k个脉冲回波可形成如图2所示三维数据，其中因发射频率分集，每个阵元可形成N个通道回波，若将第k个脉冲第l个距离采样回波写为向量yk,l∈NN×1，则其可表示为

图2 OFDM-MIMO雷达回波三维数据结构示意图Fig.2 Schematic diagram of OFDM-MIMO radar echo 3D data structure

yk,l=[yk,11,yk,12,…,yk,1N,yk,21…,yk,NN]T

=ζk,la(θ,r)⊗b(θ)+ξk,la(θj,rj)⊗b(θj)+Vk,l

(11)

式中，Vk,l∈NN×1为噪声向量，ζk,l和ξk,l分别为第k个脉冲第l个距离单元采样的目标和干扰复幅度，a(θ,r)∈N×1和b(θ)∈N×1分别为发射和接收导向向量，分别可表示为

ζk,l=α′sinc[B(tl-2τT,k)]exp[j2π(k-1)fdTr]

(12)

ξk,l=β′sinc[B(tl-2τj,k)]exp[j2π(k-1)f′dTr]

(13)

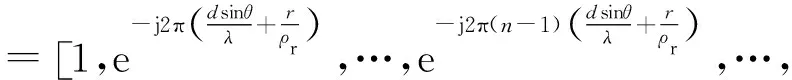
(14)

(15)

很明显，由式(11)～(15)可以看出，对于主瓣干扰而言，目标角度近似等于干扰角度(θ≈θj)，而距离r≠rj，因此，假设有一个目标位于(θs,rs)，有Q个转发式干扰机共释放P个转发式干扰目标干扰(Q≤P)，第k个转发式干扰机位于(θjk,rjk)，整个阵列接收的信号可表示为

x=xs+xj+n

(16)

基于MVDR的加权矢量为

(17)

式中，μ为常数，Ri+n为干扰加噪声协方差矩阵。这里需要说明的是，vs是空域θs和距离域rs的二维导向矢量。

传统MVDR算法，就是直接将各结构导向矢量代入式(17)，求解最优加权矢量。对OFDM相控阵雷达结构，阵列输出为

=wH[a(Rs)*a(θs)]s(t)+

(18)

式中，Rs是信号协方差矩阵，Ri为干扰协方差矩阵，s(t)是目标信号，a(θ)=[1 e-j(2πf0dsinθ/c)…e-j(N-1)(2πf0dsinθ/c)]，a(R)=[1 ej(2πΔfR/c)… ej(N-1)(ΔfR/c)], “*”表示Hadamard积。将导向矢量代入式(10)，得接收端加权矢量为

(19)

输出信干噪比(signal-interference-noise-radio,SINR)可为：

(20)

对OFDM-MIMO雷达结构，阵列输出可表示为

y(t)=wH[a(Rs,θs)⊗b(θs)]s(t)+

(21)

式中，a(Rs,θs)、a(Ri,θi)与式(18)中相同，b(θ)=a(θ)。由式(21)可得，相比于相控阵和OFDM-BFF结构，OFDM-MIMO结构同时兼具了两种结构在干扰抑制方面的优势，干扰抑制能力更强，此时，接收端加权矢量可表示为

(22)

同时，观察式(21)和发射导向向量式(14)不难看出，当发射信号频偏为0时，a(R,θ)将与距离R无关，退化为a(θ)，即相控阵雷达情况。

2 基于自适应处理算法的抗主瓣转发式干扰原理分析

本文采取的自适应处理算法与传统的空时自适应处理算法有区别。传统的空时自适应处理是利用杂波与目标在空域与多普勒频域两个维度的差异来抑制杂波，而本文的自适应处理是利用干扰与目标在角度域与距离域的差异来抑制干扰。尽管如此，本文自适应处理算法仍可借鉴传统空时自适应处理算法[2]。

在OFDM-MIMO雷达中，考虑到密集转发式干扰目标在慢时间上是独立同分布的，可以通过不同脉冲得到的快拍数据构造协方差矩阵，即

(23)

其中，L为脉冲数，xi为第i个脉冲的训练数据。

对Ri+n进行特征分解，可得

(24)

式中，λk为第k个特征值，uk为第k个特征值对应的特征向量。 特征值按大小顺序排为：λ1≥λ2≥…≥λp≥λp+1=…=λN。 不同特征值对应的特征向量正交，故可构成如下标准向量组：

(25)

由于这些密集转发式干扰目标干扰都具有相同的导向矢量，虽然有P个干扰，但实际上在对Ri+n特征分解后却只能得到Q个大特征值。 对应Q个大特征值的特征向量可形成干扰子空间，其正交基为[u1,u2,…,uQ]，其余对应N-Q个小特征值的特征向量可形成噪声子空间，其正交基为[uQ+1,uQ+2,…,uN]，干扰子空间和噪声子空间正交。

用特征值和特征向量表示Ri+n的逆可得

(26)

得最优权矢量表达式为

(28)

需要指出的是，由于OFDM方向图具有角度-距离耦合性，所以无论目标与转发式干扰机位于不同角度、相同或不同距离(副瓣干扰：θjk≠θs，rs=rjk或rs≠rjk)，还是同一角度、不同距离(主瓣干扰：θjk=θs，rs≠rjk)，这都使得信号导向矢量vs与转发式干扰机产生的干扰的导向矢量vj张成的空间并无交连，因此，目标导向矢量不与噪声子空间正交，即wΗvs≠0。

经过滤波之后，输出的信号可表示为

y=wΗx

=ξswΗvs+wΗn

(29)

输出的信号只含有目标和噪声，干扰被抑制掉了。

数字波束的输出性能常用输出SINR表示：

(30)

为解决式(17)在MIMO中直接应用算法复杂度过高的问题，充分利用MIMO导向矢量中的克罗内克结构，采用自适应算法进行最优权矢量求解，即将MIMO波束形成过程虚拟为发射波束形成和接收波束形成两个过程，两过程导向矢量分别为a(R,θ)和b(θ)，利用式(17)分别求取对应过程的最优权矢量，再求取两权重矢量的克罗内克积作为最终的权重矢量。由式(30)可看出，自适应相当于对单一子阵、子列分别进行MVDR波束形成，然后通过克罗内克积综合为一个权矢量。假设OFDM-MIMO拥有M个阵元，利用式(22)需求解M2个系数向量，而利用式(30)仅需求解2M个系数向量，大大减少了计算复杂度。

3 仿真分析

3.1 仿真1：传统MVDR算法在相控阵及MIMO雷达结构中的应用

首先对MVDR在传统相控阵中的应用进行探究。设相控阵含51个阵元，目标角度θs=30°，干扰角度θi，信噪比SNR=10 dB，干噪比JNR=30 dB，利用MVDR进行空间波束形成，得到不同θi下的角度维方向图如图3所示。从中看出，不论θi怎样变化，MVDR算法均能在θi处形成零限，当θi为35°、40°时，方向图在目标位置处增益未发生明显变化，仅零限位置发生了变化，但当干扰与目标位置进一步接近时，目标位置处的增益随干扰的接近而降低，主瓣也发生了分裂。这说明相控阵的波束形成仅能进行角度维干扰抑制，当干扰与目标角度相近时，会出现主瓣畸变、目标处增益降低等问题。

图3 不同θi下的相控阵雷达接收方向图Fig.3 Receiving pattern of phased array radar under different θi

然后对MVDR在MIMO中的应用进行探究。设目标角度θs=30°，干扰角度θi=40°，信噪比10 dB，干噪比30 dB，改变阵元数N，利用MVDR分别求解N取7、9、11、21时的最优权矢量，得阵列输出如图4所示。

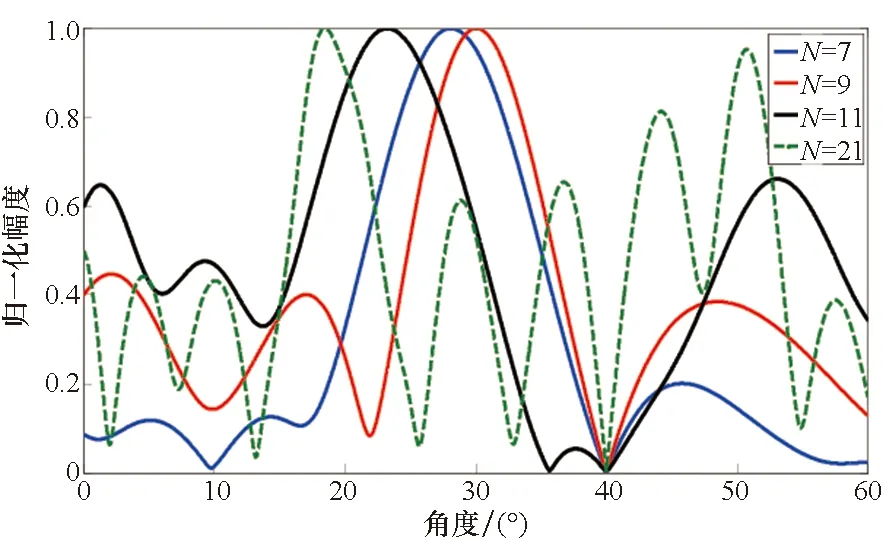
图4 不同N下的MIMO雷达接收方向图Fig.4 MIMO radar receiving pattern under different N

假设天线阵列总长度不变，阵列输出结果随着N的缩小而稀疏重排为N元均匀线阵。由图4看出，不论N怎样变化，利用MVDR算法进行MIMO雷达波束形成，总能在干扰位置处形成零限，表明MVDR具有良好的干扰抑制性能。但是，随着阵元数的增加，主瓣峰值相对目标角度的偏移量逐渐增大，同时，最大副瓣能量不断增高，N=21时，方向图已没有真正意义上的主瓣。同时，噪声、干扰协方差矩阵Ri+n的维数为N2，当N较大时，矩阵维数很高，求逆运算的运算量较大，最优权矢量求解困难。这都表明MVDR算法不适用于大规模MIMO结构。

3.2 仿真2：自适应算法在OFDM相控阵雷达结构中的应用

设OFDM相控阵雷达阵元数为51，频差Δf=10 kHz，目标位于(Rs,θs)，Rs=30 km，θs=30°，干扰位于(Ri,θi)处，Ri=32 km，θi=30.5°，相控阵PAR(Δf=0)、OFDM相控阵雷达(OFDM-BFF)接收方向图如图5所示。由图看出，对相控阵，在干扰角度形成了一条清晰的“零限带”，“零限带”在角度维呈直线分布，干扰与目标角度接近时，“零限带”不可避免地对目标方向增益产生影响；而由于频差的引入，OFDM波束发生“倾斜”，在干扰距离上形成零限的同时，能够在目标位置保持增益。这种波束空域分布自由度的提高，为平台外干扰抑制提供了更多途径。

(a) 相控阵(a) Phased array

(b) OFDM相控阵雷达(b) OFDM phased array radar图5 雷达天线方向图Fig.5 Radar antenna pattern

改变干扰位置，设干扰位于(32 km,42°)处，利用MVDR进行波束形成(为方便观察，将阵元数降为9)，得OFDM相控阵雷达波束如图6所示。由图看出，此时，OFDM相控阵雷达形成的主瓣在目标位置处依然发生了畸变，这是因为干扰依然位于OFDM相控阵雷达的空域主瓣内(如图6(a)所示)。由此说明OFDM相控阵雷达也面临主瓣畸变问题，当干扰距离、角度与目标位置满足OFDM相控阵波束分布的距离、角度耦合关系时，同样会出现波束形成器输出性能下降的问题。

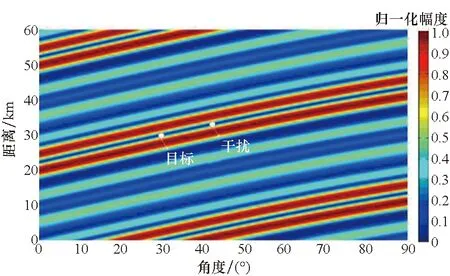
(a) 三维方向图(a) 3-D

(b) 二维方向图(b) 2-D图6 OFDM相控阵雷达天线方向图Fig.6 Antenna pattern of OFDM phased array radar

3.3 仿真3：自适应算法在OFDM-MIMO中的应用

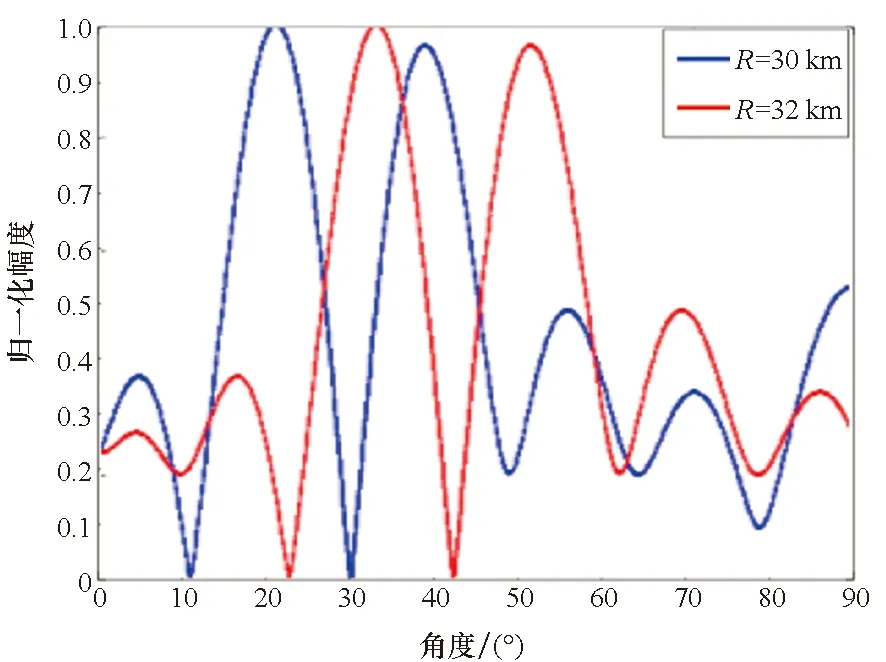
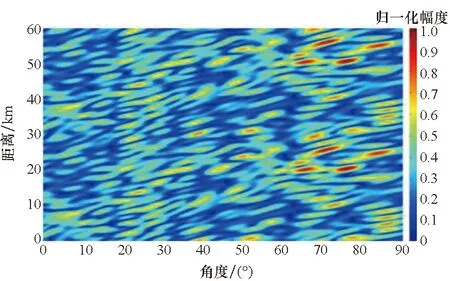
首先探究传统MVDR算法在OFDM-MIMO中的应用性能。设OFDM-MIMO阵元间频差Δf=10 kHz，目标位置Rs=30 km、θs=30°，干扰位置Ri=33 km、θi=33°，分别设阵元数为9、31，求解MVDR权矢量，得到对应的三维方向图及干扰、目标距离处的角度维方向图如图7、图8所示。由图看出，当N=9时，利用MVDR能够得到理想的方向图，方向图在目标处增益最大，在干扰处增益置零；当N=31时，虽然也能在干扰位置处形成零限，但方向图已经出现较大程度畸变，图中已找不到相应的主瓣区域。

(a) 三维方向图(a) 3-D

(b) 二维方向图(b) 2-D图7 N=9时MVDR求取的OFDM-MIMO方向图Fig.7 OFDM-MIMO pattern obtained by MVDR at N=9

(a) 三维方向图(a) 3-D

(b) 二维方向图(b) 2-D图8 N=31时MVDR求取的OFDM-MIMO方向图Fig.8 OFDM-MIMO pattern obtained by MVDR at N=31

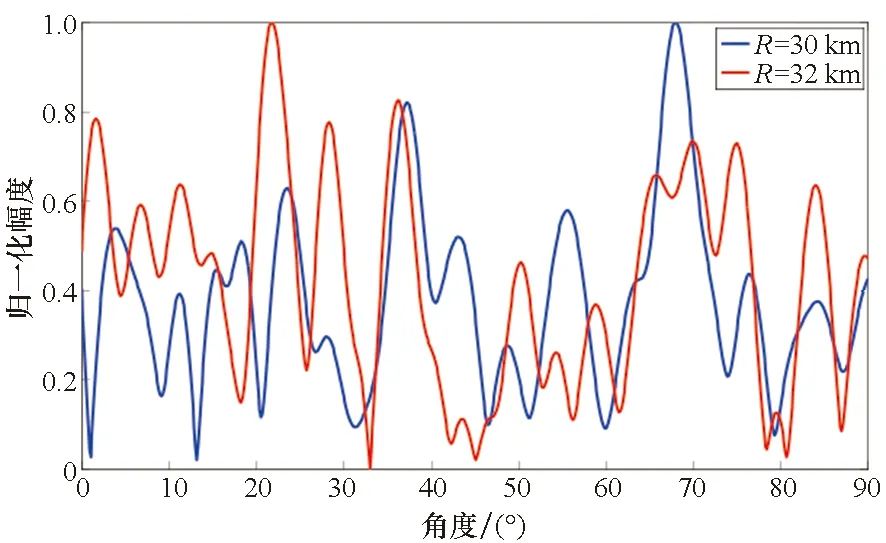
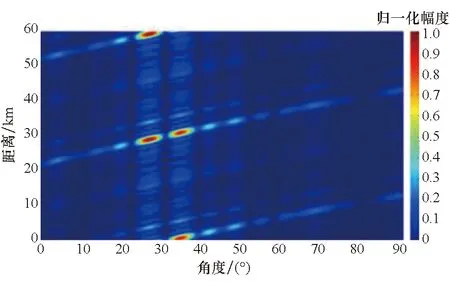
然后对自适应算法在OFDM-MIMO中的应用性能进行仿真。阵元数为31，干扰位置分别为(33 km, 33°)和(33 km, 31°)，其余仿真参数不变，利用式(30)求OFDM-MIMO的最优权矢量，得不同干扰角度下的阵列输出方向图如图9～10所示。

(a) 三维方向图(a) 3-D

(b) 二维方向图(b) 2-D图9 θi=33°时自适应求取的OFDM-MIMO方向图Fig.9 OFDM-MIMO pattern obtained adaptively when θi=33°

(a) 三维方向图(a) 3-D

(b) 二维方向图(b) 2-D图10 θi=31°时自适应求取的OFDM-MIMO方向图Fig.10 OFDM-MIMO pattern obtained adaptively when θi=31°

由图9可看出，利用自适应时，即使阵元数较大也能形成理想的方向图，在保持目标位置增益的同时，较好地抑制主瓣；但由图10可看出，利用自适应算法进行波束形成，当干扰与目标角度相近时，方向图主瓣依然发生了畸变，这是因为自适应算法是由两波束形成过程分别求解，然后求取克罗内克积得到，当干扰与目标角度相近时，虚拟接收波束主瓣畸变，从而使最终的波束主瓣发生畸变。而由上述分析和图6可得，OFDM-MIMO具备二维空域的干扰抑制能力，只要干扰与目标在距离、角度一维可分辨，就能够在保持目标增益的同时对干扰进行抑制，因此，OFDM-MIMO的干扰抑制潜力还有待进一步挖掘。

3.4 仿真4：各类结构的输出性能对比

首先对方向图进行比较，统一设定阵元数N=9，目标位置Rs=30 km、θs=30°，干扰位置Ri=33 km,θi=33°，阵元间频差Δf=10 kHz，利用MVDR算法求取相控阵(PAR)、OFDM-BFF、OFDM-MIMO(分别用传统MVDR和自适应算法)的最优权矢量，在目标、干扰距离处各结构的角度维方向图如图11所示(为方便比较主瓣偏移情况和干扰的零限深度，目标距离处采用幅度图，干扰距离处采用分贝图)。

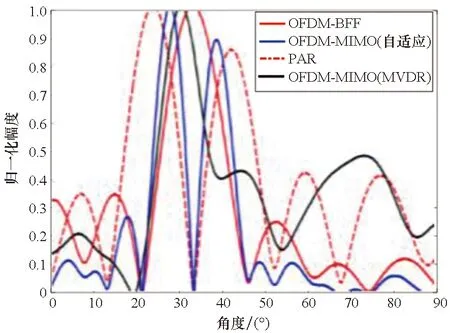
(a) R=30 km

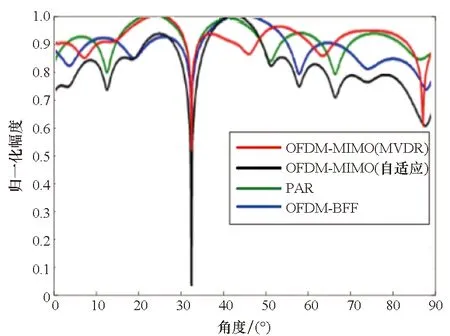
(b) R=32 km图11 各结构的角度维方向图Fig.11 Angle dimension pattern of each structure

其次对结构的输出信干噪比性能进行比较，改变干扰角度和阵元数量，分别求取各类结构的输出信干噪比，结果如图12所示。

(a) N=9

(b) N=21图12 不同干扰角度下各结构的输出信噪比Fig.12 Output SNR of each structure under different interference angles

由图11可知，在目标距离处，PAR、OFDM-MIMO(自适应)形成的波束均发生了主瓣峰值偏移和形状畸变，而OFDM-BFF、OFDM-MIMO(MVDR)在目标处均保持了较高增益。在干扰距离上，OFDM-MIMO(自适应)形成的干扰最深，其余结构相当，这是因为OFDM-MIMO(自适应)将整个波束形成过程虚拟成发射与接收波束形成两个过程，相当于对干扰进行了两维抑制，而OFDM-MIMO(MVDR)，因为一定程度保持了主瓣形状，在接收波束阶段减轻了对干扰的抑制程度，因此零限要浅。这也从侧面说明，阵元数较小时，OFDM-MIMO(MVDR)拥有一定的主瓣保形能力。

由图12看出，不论干扰角度如何，OFDM-MIMO(MVDR)的输出SINR均高于其他三种类型，且随着阵元数的增加而增加。对PAR结构与OFDM-BFF结构，各存在SINR输出的“凹口”，出现凹口的原因是因为主瓣畸变，前述仿真中已进行了分析。多数情况下，OFDM-MIMO(自适应)得到的波束方向图能获得比PAR和OFDM-BFF要优的输出SINR性能，但是在PAR和OFDM-BFF的“凹口”处，OFDM-MIMO(自适应)方向图SINR性能均会出现下降，性能介于PAR和OFDM-BFF两者之间，这说明OFDM-MIMO(自适应)较PAR和OFDM-BFF更容易出现SINR“凹口”。

4 结论

本文主要针对OFDM雷达主瓣转发式目标干扰的鉴别抑制原理以及基于自适应处理算法的抗主瓣干扰原理的必要性进行研究分析，重点分析了OFDM-MIMO，从理论分析和仿真中可以发现OFDM-MIMO雷达可有效解决主瓣密集转发式干扰目标干扰抑制问题。能够说明本文提出的算法具有以下特点：

1)具有良好的主瓣保形能力，即使当干扰与目标同处于发射或接收波束主瓣时，也不会出现主瓣畸变、目标处增益性能下降的情况。

2)对干扰具有良好的抑制能力，只要干扰与目标在距离或角度上一维可分，失配的目标导向矢量会产生目标信号相消、输出SINR急剧下降的问题。本文算法能够在保持目标处较大增益的同时，对干扰形成抑制。

3)能够应用于阵元数较多的阵列中。