2022年高考全国理综乙卷物理第25题解析及启示

李林静，钱长炎，刘成欣

安徽师范大学物理与电子信息学院，安徽 芜湖 241002

我国高等学校入学考试（简称“高考”）理科综合试卷（简称“理综卷”）物理试题既要体现物理课程标准的目标，又要反映高考改革的走向。高考评价体系和普通高中物理课程标准中的核心素养目标无疑是高考试题命制的重要依据。高考评价体系提倡高考试题由“知识能力立意”评价向“价值引领、素养导向、能力为重、知识为基”评价转变，这些要求在2022年高考理综乙卷的综合应用题中得到较为充分的体现。

2022年高考全国理综乙卷物理第25题作为综合应用题，考查了动量定理、动能定理、能量守恒定律、动量守恒定律、牛顿运动定律等物理规律及综合应用。如何在学科核心素养目标的指导下，通过试题分析促进高考评价体系在教学实践中落地，一直以来备受广大物理教育研究者和高中物理教师的关注。鉴于此，本文对该试题的命题意图、解析和学生的典型错误及成因进行深入分析与探讨，以期为我国高中物理教学探索切实可行的方法和途径。

1 原试题及其命题意图分析

2022年高考全国理综乙卷物理第25题共设置三个小问，遵循了物理压轴题分层设问、层层递进的原则，原试题如下。

如图1（a）所示，一质量为m的物块A与轻质弹簧连接，静止在光滑水平面上；物块B向A运动，t＝0时与弹簧接触，到t＝2t0时与弹簧分离，第一次碰撞结束，A、B的v-t图像如图1（b）所示。已知从t＝0到t＝t0时间内，物块A运动的距离为0.36v0t0。A、B分离后，A滑上粗糙斜面，然后滑下，与一直在水平面上运动的B再次碰撞。之后A再次滑上斜面，达到的最高点与前一次相同。斜面倾角为θ（sinθ＝0.6），与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求

图1 原试题插图

（1）第一次碰撞过程中，弹簧弹性势能的最大值；

（2）第一次碰撞过程中，弹簧压缩量的最大值；

（3）物块A与斜面间的动摩擦因数。

第25题依托“一核四层四翼”的高考评价体系［1］，属于典型的多物体、多过程的综合应用题，其分析如表1所示。该试题将碰撞模型、弹簧模型与斜面模型相结合，需要利用v-t图像综合分析多个物体的运动过程及碰撞过程，具有一定的难度。

表1 基于“四层四翼”的高考评价体系的第25题分析

根据表1，问题（1）考查了动量守恒定律和能量守恒定律的综合应用。重点考查学生从图像中获取信息、加工信息并利用有效信息进行合理推断的能力［2］。需要学生正确地理解试题信息及v-t图像，从图像中提取两个物块碰撞前后的速度大小以及达到的共同速度大小和时刻等关键信息，对学生信息处理能力要求较高，同时也为后面问题的解决做了初步的准备。

对于问题（2），当弹簧弹性势能达到最大值时，弹簧压缩量也为最大值，v-t图像下的面积对应物块运动的位移。对于学生而言，最大的难点在于物块A和B在做非匀变速直线运动，需要运用“微元法”将复杂的、不便于直接求解的运动转化为简单的、便于求解的运动学模型［3］。可有效地考查学生综合运用知识的能力和水平，同时对学生的模型建构能力和应用数学处理物理问题的能力有较高的要求。

问题（3）需要学生灵活运用运动学的知识对物块A滑上斜面再下滑的运动过程进行分析，考查学生对于匀变速直线运动、牛顿第二定律和动能定理等重要概念和规律的理解和应用，从而达到对学生训练和选拔的目的。

该试题的三个小问相互关联、层层递进，全方位地检测了学生对于必备知识理解的深度及关键能力、学科素养与核心价值的具备程度［4］。为了进一步探究该试题，有必要对其解析过程及学生易错点进行分析。

2 2022年高考理综乙卷物理第25题解析过程及学生易错点

依据上述命题意图，我们依据第25题解题思路框架，深入探讨该试题的解析方法。为了解学生在解答时的困难所在，对部分考生进行了访谈调查，找出学生的易错点，从而对该试题进行更为深入和全面的解析。

2.1 第25题解析基本思路

学生解题的过程是获取试题信息、建构物理模型的过程。通过建构物理模型可以简化试题中的已知条件，将问题情境数学化，提高学生的解题效率，培养学生的逻辑思维能力［5］。受到相关研究的启发［6］，第25题的解析思路框架如图2所示。

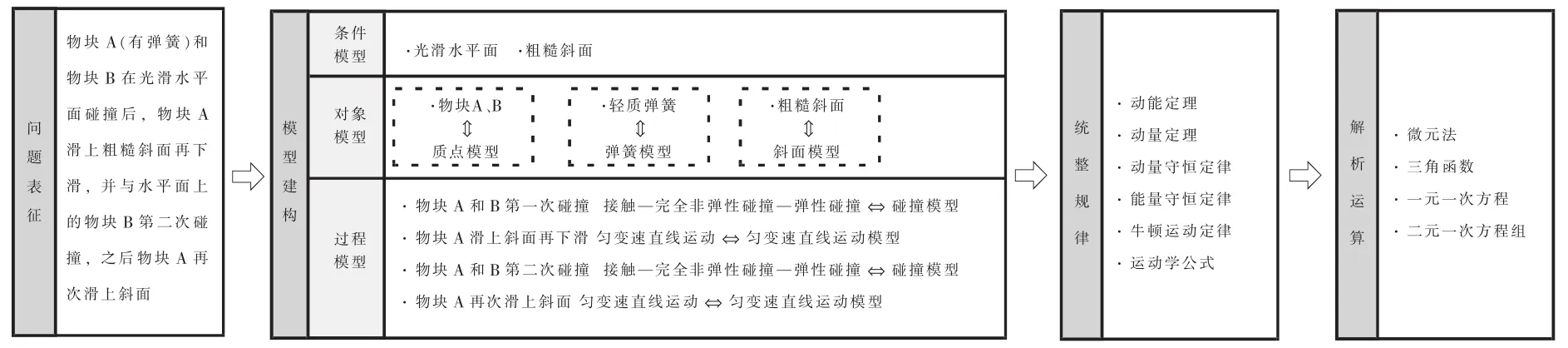
图2 第25题解析思路框架示意图

该解题思路框架主要由四部分构成：问题表征、模型建构、统整规律和解析运算。

问题表征是指形成问题空间，包括明确问题的给定条件、目标和允许的操作［7］。学生在解答该试题时需要将问题情境正确地表征为物理问题，通过图像表征提取v-t图像中的关键信息，用于分析和解决问题。

近年来，高考物理十分重视对物理模型与模型建构能力的考查，也注重通过多种模型的组合来检验学生的模型建构能力［8］。该试题将弹簧模型、斜面模型和碰撞模型相结合，学生可以根据试题信息先建立条件模型和对象模型；再通过具体分析物体的运动过程和碰撞过程建立过程模型；最后统整规律将物理问题数学化，并建立方程解析运算。

因此，我们将依据上述解析思路框架，对该试题的解析过程进行分析。

2.2 问题(1)的解析过程及学生易错点

在第一次碰撞过程中，当v-t图像中物块A和B的速度相等，即发生完全非弹性碰撞时，弹簧的弹性势能达到最大，因此可运用动量守恒定律和机械能守恒定律解析。

设物块A的质量为mA，物块B的质量为mB，初速度为vB。

由动量守恒定律得

由机械能守恒定律得

联立（1）和（2）式得

根据访谈结果，学生易犯的错误包括：（1）误将物块B的质量当作m；（2）不理解v-t图像中物块A和B的速度相等时，弹簧的弹性势能达到最大；（3）误认为弹簧的弹性势能为末状态物块A和B的动能之和或动能之差。

2.3 问题（2）的解析过程及学生易错点

在第一次碰撞过程中，弹簧的压缩量最大值即为0到t0时刻物块A和B的位移之差，具体三种解析过程如下。

2.3.1 问题（2）的三种解析过程及学生易错点

方法一：运用“微元法”和动量定理解析

从0～t0时间内，设物块A相对于地面的位移为xA，物块B相对于地面的位移为xB，弹簧原长为l0，压缩后长度为l，形变量为Δx，弹簧弹力为F，如图3所示。

图3 第一次碰撞弹簧最大压缩量示意图

以物块A为研究对象，由动量定理得

同理得

联立（5）和（6）式

对（7）式两边同时乘以Δt并求和得

由图3中几何关系得

联立（9）—（12）式得

方法二：运用“微元法”和动量守恒定律解析

对（1）式两边同时乘以Δt并求和得

联立（3）（11）（12）和（15）式得

方法三：运用质点系动力学方程解析

以物块A和B为整体，可运用质点系动力学方程进行解析，该方法过程清晰、方程简单、计算量较小［9］。

当t=0时，质心C到物块A的距离为lA，到物块B的距离为lB；当t=t0时，质心C到物块A的距离为l'A，到物块B的距离为l'B，物块A向质心C运动的距离为x'A，物块B向质心C运动的距离为x'B，如图4所示。

图4 第一次碰撞质心位置不变示意图

由质心位置公式可得

由运动关系得

由图4中几何关系得

联立（12）和（18）—（24）式得

通过访谈，以上三种解析方法中学生的易错点为：（1）应用数学处理物理问题的能力不足，只列出相关公式，未能正确求解［10］；（2）误将弹簧的形变量当作物块A和B位移之和或位移之差的一半；（3）忽视了题干信息，利用胡克定律计算弹簧压缩量最大值。

2.3.2 问题（2）一种常见错误解析及学生易错点

由牛顿第二定律得

由运动学公式得

联立（3）和（26）—（29）式得

若采用平均加速度分析，则

这种解法中，学生常见的易错点为：误将v-t图像中物块A和B的运动过程当作匀变速直线运动，利用平均加速度进行计算。

2.4 问题（3）的解析过程及学生易错点

物块A滑上粗糙斜面再滑下的过程，为匀变速直线运动；当物块A和B发生第二次碰撞后两物体分离的过程，可视为弹性碰撞，具体两种解析过程如下。

方法一：运用匀变速直线运动规律解析

设物块A和B第一次碰撞后完全分离的速度为vA1，vB1，第二次碰撞后完全分离的速度为vA2，vB2，物块A滑下斜面底端的速度为v'A，物块A上滑的距离为s，上滑时的加速度为a1，下滑时的加速度为a2。

物块A和B第二次碰撞后，由动量守恒定律得

由机械能守恒定律得

由于物块A第二次滑上斜面也能到达第一次的高度

上升时由牛顿第二定律得

由匀加速直线运动公式可得

下滑时同理可得

联立（3）和（34）—（40）式得

方法二：运用能量守恒定律解析

物块A滑上斜面又下滑的过程中，由能量守恒定律得

联立（34）—（38）和（42）式得

依据访谈结果，学生的易错点为：（1）未能注意题目中的“粗糙斜面”和“上滑到相同高度”等条件；（2）忽略物理量的矢量性，在第二次碰撞过程中没有考虑速度的方向；（3）受力分析错误，误认为物块A所受的摩擦力方向均沿斜面向下。

鉴于上述分析，尽管三个问题考查的必备知识、关键能力、学科核心素养和核心价值侧重不同，学生的解题策略也存在差异，但是学生的易错点存在相似之处，因此，我们有必要对学生的典型错误及成因进行分析，从而更好地指导教学实践。

3 学生典型错误及成因分析

在对第25题命题意图、解析思路和解析分析的基础上，我们对访谈中的学生易错点进行梳理，并着重分析典型错误，深入探讨其成因，主要包括以下几个方面：

第一，问题表征能力不足。学生在解题时不能正确地表征题意，仅生搬硬套相关物理公式，不能灵活地结合v-t图像和题干信息进行解答。其原因可能是在习题教学中，教师通常将试题中的关键信息和已知条件直接呈现给学生，学生缺乏对于问题情境的独立思考，不能准确地将问题情境表征为物理问题，因此无法将题干信息与所学知识进行识别和匹配。

第二，模型建构能力较为薄弱。学生在解答该试题时，对象模型的建构存在问题，过程模型选用不当。究其原因，一方面，教师对于学生模型建构能力的培养不够重视；另一方面，高考是限时答题，要求学生对于考查的物理模型非常熟悉，能在考试中迅速地建构合适的模型，并且准确地解决相关问题。

第三，应用数学处理物理问题的能力欠缺。根据访谈发现，部分学生认为该试题难度较大，在解答时仅能列出相关物理公式，却无法计算得出正确结果。其原因为该试题中用字母符号表征已知条件，需要结合v-t图像中的数据，运用“微元法”进行解答，要求学生具有一定的数学计算功底以及应用数学处理物理问题的能力［11］。因此，教师要注重跨学科教学，在教学中加强物理和数学之间的联系。

4 小结与启示

第25题重点考查了学生的问题表征、模型建构和应用数学处理物理问题的能力，其命题方式凸显出“价值引领、素养导向、能力为重、知识为基”的新理念。通过对该试题的命题意图、解析和学生典型错误及成因分析，无疑对新课程改革背景下的物理教学有一定的启发作用。

首先，重视物理必备知识，充分发挥教科书在教学中的基础性作用。教科书作为学生最主要的学习资源，不仅能向学生提供较为系统的物理知识，其编排逻辑也符合学生的认知规律。因此，教师在教学中应依托教科书、吃透教科书、拓展教科书，并要求学生掌握在物理关键能力和学科素养的养成过程中必须具备的可迁移的知识。

其次，创设问题情境，培养学生理解、推理论证和模型建构等关键能力。近些年，高考物理综合应用题越来越注重问题情境的考查。教师在教学中要合理创设情境，设置新颖的试题呈现方式和设问方式，引导学生对试题进行正确表征，建构合适的模型，促进学生科学思维的发展。

最后，重视对经典试题的剖析，寻求多样化的问题解决思路。利用v-t图像综合分析多个物体在斜面上运动及碰撞问题在2019年全国理综卷Ⅰ第25题已经考查过，然而从图像中提取关键信息以及对碰撞过程的分析仍是学生容易出错的环节。在复习备考时，教师应重视对历年的高考物理综合应用题的剖析，启发学生从多个角度思考问题并寻求最优解，提高解答的效率，培养学生应用数学处理物理问题的能力。