重构规律教学逻辑 提升科学探究能力——以人教版必修第二册“向心力”一课为例

王祥东，张津玮，申琳娜

重庆复旦中学，重庆 400015

物理规律是整个物理学知识体系的基础，物理规律教学是物理教学的核心。物理规律教学的效果如何，直接关系到学生对于物理知识的认识程度，影响到学生整体知识网络的建构与扩展。物理知识之间都是有着内在逻辑关系的，知识的形成、学生的认知也有规律，在规律教学中构建有序的教学逻辑，使之符合学生的思维发展和心理发展规律［1］，让学生在学习物理规律的过程中提升科学探究能力。

“科学探究”是指基于观察和实验提出物理问题、形成猜想和假设、设计实验与制订方案、获取和处理信息、基于证据得出结论并作出解释，以及对科学探究过程和结果进行交流、评估、反思的能力［2］。通常，规律课教学中科学探究的提出是基于问题的发现，科学探究以清晰的概念为基础，科学探究的过程注重方法，科学探究的推进讲究逻辑，科学探究的归宿是要解决问题。

“向心力”是人教版教材中一节典型的规律教学课。在学习这节内容之前，学生认识了匀速圆周运动的特点，了解了转速和周期，知道了线速度和角速度的物理意义及其关系。“向心力”一节的重点是通过实验探究影响向心力大小的因素，得出向心力大小的表达式，并能够解决实际问题；难点是向心力概念的建立与理解，以及向心力来源的分析。为了助推学生科学探究能力的提升，将本节课的教学推进逻辑进行重新构建，如图1所示。

图1 教学推进逻辑示意图

1 创设情境——激发学生认知冲突

视频播放:游乐场里“飞椅与人”一起在空中稳定飞行，如图2所示。

图2 飞椅与人一起转动示意图

层进设问：此时空中的“飞椅与人”整体做的什么运动？“飞椅与人”整体受到了哪些力？这些力的合力指向什么方向？大小有什么特点？

设计意图：创设“游乐场里空中飞椅”这一真实的物理情境，通过感性材料打开学生的认知，为建立概念和探究规律作准备。将问题指向“所受合力的方向和大小有什么特点”，激发学生的认知冲突，充分体现“创设情境是为了引导学生发现问题”这一理念，也使得接下来的科学探究“有的放矢”。

2 建立概念——向心力来源和方向

演示实验：如图3所示，小球在细线牵引下在水平桌面上做匀速圆周运动。

图3 细线牵引下小球做匀速圆周运动

层进设问：小球做匀速圆周运动时，如果绳子断了，小球还能做圆周运动吗？为什么？小球竖直方向受到的重力、支持力是什么关系？绳子给小球的作用力有什么特点？

情境设置：如图4所示，物块在水平圆盘上跟随圆盘做匀速圆周运动。

图4 物块在圆盘上做匀速圆周运动

层进设问：如果圆盘上表面是光滑的，物块还能做匀速圆周运动吗？什么力对物块做匀速圆周运动起了作用？物块与图3中的小球运动情况相同吗？它们的受力是否也应该相似？你想到了什么？

演示实验：如图5所示，小球在细绳的牵引下在空中做匀速圆周运动。

图5 细线牵引下小球在空中做匀速圆周运动

层进设问：小球运动轨迹的圆心在哪里？图5中的小球与图3中的小球、图4中的物块运动情况相同吗？它们的受力是否也应该相似？你又想到了什么？图5中的小球是否真的受到一个指向圆心的力？从力的合成角度看，这个力是什么？从力的分解角度看，这个力又是什么？向心力是否一定是一个真实的力？什么力可以提供向心力？

建立概念：做匀速圆周运动的物体所受的合力总指向圆心，这个指向圆心的力就叫作向心力。

设计意图：相对于教材，这里又增加了图4和图5两种情境，让学生在足够多的感性认识基础上，通过层进设问，准确理解：物体做匀速圆周运动的合力指向圆心，合力不改变速度的大小只改变速度的方向；向心力是变力，可由单个力提供，也可由几个力的合力提供，或者由某个力的分力来提供。物理规律的学习都是以准确的物理概念为基础，通过构建“向心力”的清晰概念，为科学探究向心力的大小作铺垫。

3 探究规律——猜测、探究、验证

3.1 猜——定性猜测

改进实验：将教材“感受向心力”的沙袋实验（图6左图）进行改进，在竖直细绳下端固定一个弹簧秤（图6右图）。

图6 感受向心力”实验示意图

层进设问：为了探究一个物理量与多个物理量间的关系，通常采用什么研究方法？保持绳长和沙袋质量不变，改变沙袋转动的快慢，向心力有怎样的定性变化？保持沙袋质量和转动快慢不变，改变绳长，向心力有怎样的定性变化？保持沙袋转动快慢和绳长不变，改变沙袋的质量（换用质量较大的沙袋），向心力有怎样的定性变化？上述实验能得到向心力与这些物理量的定量关系吗？

设计意图：通过增加竖直弹簧秤对教材实验进行改进，可较为直观地显示向心力 (近似为拉力)的变化。实验过程中进行层进设问，也使得学生能充分体验“控制变量法”这一科学探究方法。学生科学探究能力的培养总是从获得直接感性认识开始的，通过“感受向心力”这个定性实验，让学生体验影响向心力的因素，为接下来进行的“探究向心力大小与半径、角速度、质量的定量关系”的实验设计提供了方向。

3.2 探——定量探究

实验探究：如图7所示，通过向心力演示仪用控制变量法探究向心力大小与半径、角速度、质量的定量关系。

图7 向心力演示仪

层进设问：在图7所示的向心力演示仪中，向心力的大小怎样测量？如何改变物体的质量？如何设定轨道半径？如何控制两边变速塔轮的角速度？你设计的实验步骤是怎样的？得到了怎样的实验结果？你还能写出怎样的表达式？（得出

设计意图：进行实验探究的重要前提是弄清向心力演示仪的工作原理，通过层进设问使学生明白小球的向心力由横臂的挡板对小球的压力提供，小球对挡板又有反作用力，通过横臂的杠杆作用使弹簧测力套筒下降，从而露出标尺，标尺上露出的红白相间等分格子就可以显示出两个小球所受向心力的比值；同时，还要让学生明白质量、半径、角速度的倍数设定，通过控制变量法，分别研究向心力F与三者之间的关系。这正是学生在感知、猜测的基础上，将科学探究付诸实践的过程，能让学生感受到科学探究的方法和过程。

3.3 验——精准验证

DIS实验：如图8所示，应用DISLab传感器，仍然用控制变量法验证向心力大小与半径、角速度、质量的定量关系Fn=mω2r。

图8 验证向心力大小的DIS实验装置图

层进设问：我们得到的向心力公式Fn=mω2r是准确的吗？可不可以用更精准的方式去验证这个结论？讲述DIS数字化传感器的实验原理，让学生清楚研究对象是砝码柱或砝码柱组合体。砝码柱转动过程中能保持角速度不变吗？（总是逐渐减小）先研究向心力与哪个量的关系？（角速度）需要对图像作怎样的处理？（线性化处理，如图9）

图9 向心力与角速度的关系图像

角速度总是逐渐减小，怎样研究向心力与质量的关系？（在半径一定的情况下，从不同质量对应的F-ω图线中取出角速度相同的数据点，拟合出对应的F-m图线，如图10）

图10 向心力与质量的关系图像

角速度总是逐渐减小，怎样研究向心力与半径的关系？（在质量一定的情况下，从不同半径对应的F-ω图线中取出角速度相同的数据点，拟合出对应的F-r图线，如图11）

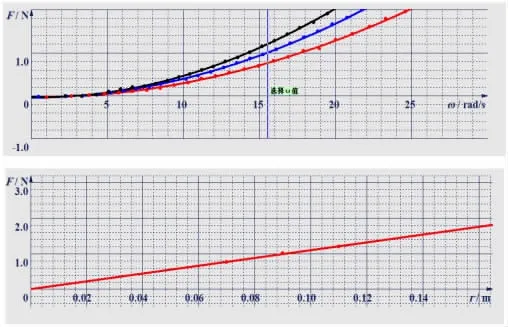
图11 向心力与半径的关系图像

设计意图：教材中是基于半径、角速度、质量的倍数关系，用向心力演示仪探究向心力的大小关系，这样得出的规律并不是很严谨，因此在探究结束后教材又指出“精确的实验表明，向心力的大小可以表示为Fn=mω2r”，通过DISLab传感器进行精确验证，让物理规律的学习过程经历“猜—探—验”的科学探究历程，使得规律的得出更加严谨。在验证向心力大小关系的过程中，根据DISLab传感器的工作原理以及“角速度总是在不断减小”这一客观事实，先探究向心力与角速度的关系，再通过半径（或质量）一定的情况下从不同质量（或半径）对应的F-ω图线中取出角速度相同的数据点，拟合得出对应的F-m（或F-r）图线，这样的探究推进逻辑本身就是科学探究素养的体现，也是控制变量法在实际问题中的具体应用。

4 理解内涵——变速圆周、一般曲线

视频播放：慢放链球运动员在掷出链球之前的加速过程，如图12所示。

图12 链球运动员掷出链球

层进设问：链球运动员在掷出链球之前的加速过程能近似看作圆周运动吗？这是匀速圆周运动吗？（定义变速圆周运动）做圆周运动需要什么方向的力？速度变大需要什么方向的力？如图13所示，Fn，Fτ来源于哪里？绳子与速度方向还垂直吗？

图13 链球加速过程的受力图

如图14所示，汽车在水平弯曲的道路上行驶，轨迹既不是直线也不是圆周（一般的曲线运动），能近似看作圆周运动吗？如果将汽车在每小段的运动看作圆周运动的一部分，且从速度计读出了汽车运动的速度，为了计算汽车的向心力，还需要知道什么物理量？

图14 汽车在水平弯曲道路上行驶

如图15所示，物体做一般曲线运动时，尽管各个位置的弯曲程度不一样，但在每小段的运动都可以看作圆周运动的一部分，在分析质点经过曲线上某位置的运动时，就可以采用圆周运动的分析方法来处理了。如果物体做一般曲线运动时保持速度的大小不变，它所受向心力的大小也不变吗？如果向心力的大小要变，原因又是什么？（曲率半径不同）

图15 一般的曲线运动的研究方法

设计意图：为了深刻理解向心力公式的内涵，通过创设真实情境进行层进设问，让学生在更一般、更广阔的背景下认识圆周运动和曲线运动。将向心力的知识从匀速圆周运动推广到变速圆周运动和一般曲线运动，从力的分解角度了解圆周运动速度大小与方向改变的原因，从极限的角度了解一般曲线运动的研究方法。因为物理规律建立以后，又需要回到生产生活现象中去解决普遍性问题，这既是深入理解规律内涵的需要，更是科学探究素养的升华。

5 解决问题——答疑解惑、实践应用

问题再现：如图16（a）所示，“飞椅与人”整体做的什么运动？“飞椅与人”整体受到了哪些力？这些力的合力指向什么方向？“飞椅与人”的向心力来源于什么？

进阶设问：某同学想通过“空中飞椅”模型来验证向心力公式，如图16（b）所示，小球绕竖直转动轴在水平面内做匀速圆周运动，图示中的r，θ和l为已知量，重力加速度为g，该同学想通过秒表再测出一物理量来达到检验目的，接下来他应该怎样操作？（测出小球运动n圈的时间t）需要验证什么等式？

图16 “空中飞椅”及其物理模型

设计意图：在解决实际问题这一环节，回到引入部分提出的问题，既首尾呼应，又能够答疑解惑；通过进阶设问对问题进行拓展，既能够检验学生对规律的掌握情况，又能够加深对规律的理解，达到教学评价的目的。科学探究的最终归宿就是要能够解决实际问题，使学生能够在实际问题中构建物理模型，并根据所学规律解决问题。

6 结束语

本文对“向心力”这一节课的教学逻辑进行了重构，通过五个严谨的推进环节，从认知冲突提出问题到建立概念、探究规律、理解内涵，再回到问题解决，展现了规律课的教学策略。通过对课本实验的改进、深挖和拓展，进行层进设问，使学生在学习物理规律的过程中体会到：科学探究起始于问题，以清晰的概念为基础，注重方法，讲究逻辑，最终归宿就是要解决问题。特别是在“探究规律”环节，让学生经历“猜—探—验”的科学探究历程，不仅能使物理规律的得出更加严谨，而且也能助推科学探究能力的提升。