基于SSA-LSTM的日光温室环境预测模型研究
祖林禄 柳平增 赵妍平 李天华 李 辉
(1.山东农业大学机械与电子工程学院,泰安 271018;2.农业农村部黄淮海智慧农业技术重点实验室,泰安 271018;3.山东农业大学信息科学与工程学院,泰安 271018)
0 引言
我国是世界上温室面积最大的国家,其类型主要分为塑料大棚、日光温室、连栋温室等[1]。2020年底我国温室面积为1.873×106hm2,其中日光温室面积占比约30%[2]。适宜的温室环境能促进温室作物的健康高效生长,利用物联网精准采集温室环境数据、设计高精度的环境预测模型是实现温室环境精准调控的关键和重要前提[3-5]。
温室环境模型主要包括机理模型和数据驱动模型两种[6-7]。其中,机理模型为根据能量守恒和质量守恒等原理构建的温室动力学模型,如文献[8]构建黄瓜温室的小气候模型描述能量和物质的传递过程,此模型能够预测自然通风条件下空气、作物、栽培基质及塑料覆盖层的温度,但此类模型不能计算温室温度和湿度的分布(空间特征);文献[9]通过构建温室建筑计算流体力学模型,实现温室环境因子的多目标、高效率优化,其中温室的结构、材料和热环境组件是主要研究对象。这两种机理建模过程存在大量的物理参数和变量,建模过程较为复杂。
由于温室系统存在时间变化缓慢的特点且温室环境的时间序列数据具有特定的变化趋势和周期特征,温室时间序列建模可用于研究数据变化的具体规律。文献[10]利用物联网、云服务和微信平台相结合的方式,设计开发了基于差分时间序列模型的温室环境监测与温度预测系统;文献[11]提出基于非线性自回归动态神经网络模型进行日光温室温度预测;文献[12]分别构建人工神经网络、非线性自回归模型和长短期记忆网络(Long short term memory,LSTM)模型对空气温度、湿度和CO2浓度进行预测,基于时间序列算法的非线性自回归模型和LSTM模型优于传统的人工神经网络模型,论证了基于深度学习的预测模型用于温室调控的可行性,此研究未详细讨论LSTM超参数调节过程,对空气湿度的预测效果较差。文献[13]利用LSTM和4个月的温度数据,提前24 h预测温室内是否会出现极端低温,预测误差小于0.8℃,此研究为单变量建模,温室内其它变量也可能对温度预测效果产生影响。
以上相关研究主要是针对温室内空气温度和湿度要素的监测和预测,而多维温室物联网数据存在体量大、计算成本高等特点,传统的LSTM模型在训练过程中依靠人工经验手动调节参数,通用性差、不确定性高,在处理高维数据时收敛速度较慢且容易陷入局部最优[14]。麻雀搜索算法(SSA)是由XUE等[15]提出,模拟了麻雀群觅食并逃避捕食者的行为而提出的群智能优化算法,其结构简单,在收敛速度和寻优精度等方面有着明显优势[16]。考虑到温室物联网数据庞大、人工经验手动调节参数不确定性高特点,本文提出一种基于SSA-LSTM的温室环境预测模型,通过物联网采集温室不同区域的环境数据,将室内小气候历史环境数据按照时间序列构造输入矩阵,输入到SSA-LSTM模型进行训练,以实现对日光温室多维环境数据的精准预测。
1 实验数据获取与处理
1.1 实验地点
实验地点位于山东农业大学(泮河校区)科技产业园区番茄日光温室(36.174°N,117.166°E),温室为下挖式新型日光温室,墙体采用砖加土垒基水泥加固,温室东西长70.0 m,南北跨度9.8 m,下挖深度0.5 m,后墙高3.8 m,脊高5 m。
1.2 物联网数据采集系统
构建温室环境物联网数据采集系统,实时、准确获取环境信息,是实现温室环境预测的前提和保障。
物联网数据采集系统主要由CPU、感知模块和传输模块等构成,感知模块完成对空气温度、相对湿度、CO2浓度、光照强度及土壤温度和湿度的测量,采用传感器相关参数如表1所示;整体系统架构如图1所示。为保证对温室环境的有效监测,将多组传感器均匀布设在温室内,其布设示意图如图2所示:以东西方向14 m、南北方向2.5 m为单位将温室均匀划分布设平面,分别在高度0.6、1.8、3.0 m进行传感器布设;为保证数据及时有效处理,布置3套物联网系统,如图2a中1#1为第1套系统的第1个空气温湿度传感器,光1为第1个光照传感器,以此类推。传感器现场布设及物联网数据采集系统上位机界面如图3所示。
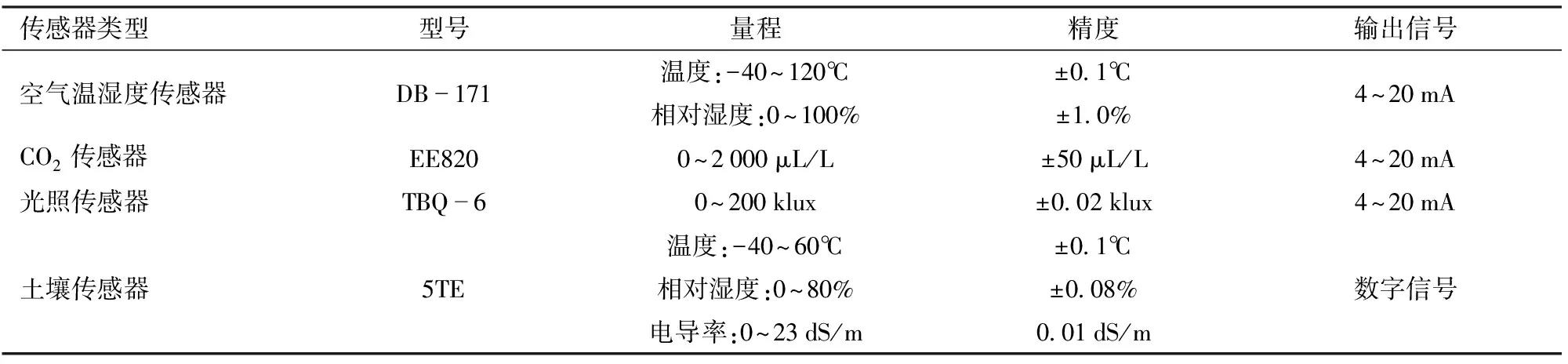
表1 物联网传感器参数

图1 物联网系统架构图
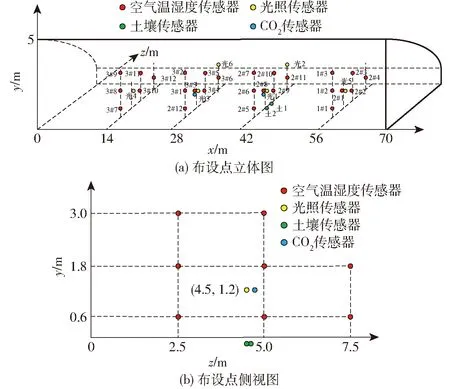
图2 传感器布设示意图

图3 物联网数据采集系统
1.3 数据预处理
1.3.1实验数据
通过上述物联网数据采集系统,自动采集空气温度、空气相对湿度、土壤温度、土壤湿度、CO2浓度(体积比)和光照强度6种数据,通过GPRS网络上传至服务器,采样时间为2020年8月1日至2021年7月31日,采样间隔为30 min,部分原始数据如图4所示(以2020年9月空气温度为例)。

图4 部分原始数据
由图4可见,实验数据存在缺失,存在温度跳变至零的现象。分析实验数据可知,数据中的缺失部分主要来自两方面,一是当天的数据记录存在缺失,二是某些时间段的数据存在缺失。
1.3.2缺失数据处理
考虑到训练数据、未来的测试数据中都可能存在缺失数据,而且它们的记录方式是相同的,避免预处理不同导致数据分布不一致问题的出现,同时对它们使用了相同的填充方式。由于存在多种缺失情况,仅使用一种方式填充可能会导致填充出现缺漏,因此本文同时使用了forward fill、backward fill与均值填充相结合的方式以保证填充覆盖率,填充前后数据对比如图5所示(以2020年9月数据为例)。由图5可见,填充后数据变化趋势保持一致,填充效果较好。
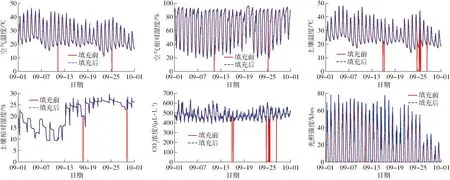
图5 填充前后数据对比
1.3.3数据归一化
为使得不同特征的数据规范到一个统一的范围,有利于神经网络的反向传播(假如不进行规范化,神经网络可能会刻意捕捉不同批次数据的变化,而忽视了预测任务本身),采用Min-Max标准化方法对数据进行归一化处理[17]。
2 SSA-LSTM环境预测模型
2.1 麻雀搜索算法
SSA是模拟麻雀群觅食并逃避捕食者的行为而提出的群智能优化算法[15]。在觅食过程中,位置是麻雀的唯一属性,觅食麻雀分为发现者和跟随者,前者搜索并发现食物,后者跟随发现者觅食;发现者和跟随者的身份是动态变化的,但所占整个种群数量的比重是不变的。同时,觅食过程还叠加了侦查预警机制,当意识到危险时,群体边缘的麻雀会迅速向安全区域移动,以获得更好的位置。
在模拟实验中,使用虚拟麻雀进行食物的寻找,假设有n只麻雀,d维待优化问题变量,适应度为f,则种群适应度可表示为

(1)
式中Xn,d——第n只麻雀d问题变量的位置
在SSA中,发现者在种群中搜索具有丰富食物的区域,提供觅食的区域和方向,发现者迭代位置更新公式为
(2)

α——(0, 1]中的均匀随机数
nmax——最大迭代次数
R2——预警值,取[0, 1]中的均匀随机数
T——警戒阈值,取[0.5, 1]
Q——标准正态分布随机数
可以看出,当R2≥T时,表示有麻雀发现了捕食者并发出了警报,此时所有麻雀都需要飞到安全位置进行觅食;当R2 跟随者会时刻监视发现者,当它们察觉到发现者找到了更好的食物,它们会立即离开现在的位置去争夺食物,跟随者位置更新公式为 (3) 其中 A+=AT(AAT)-1 式中XP——发现者占据的最优位置 Xworst——最差位置 A——1行D列的矩阵,其每一维都随机从{-1,1}中选取 L——元素均为1的1行D列的矩阵 当i>n/2时,表明第i个跟随者没有获得食物,此时需要到其它地方觅食以获得较多能量;当i≤n/2时,其取值为当前最优的麻雀的位置加上该麻雀与最优位置每一维距离随机加减后,将总和均分到每一维上。该过程可以描述为在当前最优位置附近随机找一个位置,且每一维距最优位置的方差将会变得更小,即不会出现在某一维上与最优位置相差较大,而其他位置相差较小,其值收敛于最优位置。 在麻雀觅食过程中,10%~20%的麻雀会进行预警行为,如果有危险发生,它们会放弃食物而移动到一个新的位置,预警者位置更新公式为 (4) 式中Xbest——全局最优位置 fg、fW——全局最佳和最差适应度 fi——当前麻雀适应度 β——符合标准正态分布的随机数 K——麻雀移动方向,属于[-1,1]中随机数 ε——一个较小非零数(防止分母取值为0) 从式(4)可以看出,fi>fg表示该麻雀不在最优位置,容易受到攻击,它将移动到最优位置附近;fi=fg表示当前麻雀处于最优位置,它会移动到自身附近的一个位置,具体移动距离取决于自身位置与最差位置之差和自身适应度与最差适应度之差的比值。 LSTM来源于递归神经网络(Recursive neural network, RNN)[18],可以学习长期依赖信息,且在一定程度上解决梯度消失和梯度爆炸这两个问题。 如图6a所示,RNN是重复单一的神经网络层,在其隐藏块中只有一个内部操作,例如一个tanh层,作用在于帮助调节流经网络的值,使得数值始终限制在-1~1之间。LSTM中的重复模块则包含4个交互的层,3个Sigmoid 和1个tanh层,并以一种非常特殊的方式进行交互,如图6b所示。 图6 RNN和LSTM结构 LSTM拥有遗忘门、输入门和输出门3种类型的门结构,来去除或者增加信息到细胞状态,其结构如图7所示[19]。 图7 LSTM门结构 遗忘门,决定从细胞状态中丢弃的信息,即 ft=σ(Wf(ht-1,xt)+bf) (5) 式中ft——遗忘门输出值Wf——权值 σ——Sigmoid激活函数 ht-1——上一个输出值 xt——当前输入值bf——偏差 输入层,用来确定被存放在细胞状态中的新信息,包含两方面,一是Sigmoid层称“输入门层”,决定将要更新的值;二是tanh层,创建一个新的候选值向量,会被加入到状态中。公式为 it=σ(Wi(ht-1,xt)+bi) (6) (7) 式中it——输入层门输出值 Wi——输入层权值bi——输入层偏差 Wc——候选值权值bc——候选值偏差 细胞状态,更新旧细胞状态的时间,Ct-1更新为Ct,即 (8) 输出门,确定输出的值,即 ot=σ(Wo(ht-1,xt)+bo) (9) ht=ottanhCt (10) 式中ot——输出层门输出值 Wo——输出层权值bo——输出层偏差 ht——输出层输出 在LSTM模型中,神经元个数、迭代次数、输入批量和学习率等超参数选择对模型拟合能力起着重要作用[20],而温室环境预测模型中输入数据是多维序的,传统的LSTM靠人工经验进行调参,效率低且准确性差,为使模型的性能达到最优,采用局部搜索能力极强,收敛速度较快的SSA优化算法对模型超参数进行迭代选优,算法流程图如图8所示,具体步骤如下: 图8 SSA-LSTM流程图 (1)SSA参数设置。初始化麻雀种群参数,包括麻雀种群数量、初始位置、最佳位置、全局最佳适应度等。将初始化的麻雀位置根据适应度函数评估麻雀位置并进行排序,选取前20%作为发现者,其余为跟随者,随机选取10%~20%的麻雀作为警戒者负责警戒和侦查。 (2)根据麻雀数目与优化参数(神经元个数、迭代次数、输入批量和学习率)形成搜索空间矩阵并初始化相关参数,设置最大迭代次数。 (3)根据条件式(1)~(3)更新发现者、参与者、侦察者位置,并以边界函数约束对LSTM所需超参数传参。 (4)将返回结果通过适应度函数进行位置评估,找出最优适应度个体及最劣适应度个体。若本次迭代中麻雀最佳适应度优于全局最佳适应度则用其代替,否则不变。 (5)判断是否满足设定的达到误差和最大迭代次数的停止条件。若符合,则将全局最优超参数组设为LSTM的参数;若不符合,则返回步骤(3)。 为了直观地表示SSA优化后的模型预测能力,分别使用均方根误差(RMSE)、平均绝对百分比误差(MAPE)以及拟合指数Rf作为预测模型性能评价指标[21]。 训练所使用的服务器环境如下:处理器为E5-2673V3*2,内存32 GB,GPU显卡为NVIDIA GTX3090 24G*2,操作系统64位Windows 10,编程软件为Matlab R2021a。 为更加精准地建立温室环境预测模型,采用多组传感器的平均值作为模型训练数据,实验数据采样时间为2020年8月1日至2021年7月31日,采样间隔30 min,单环境参数数据约为17 520条,按9∶1的比例将其划分为训练集和测试集。构建输入输出同为6参数的多维数据预测模型,同时对温室内6种参数进行训练和预测。 优化训练参数设置如下:SSA中麻雀总数为30,发现者占比20%,警戒者占比15%;隐含层神经元数m搜索范围[100, 500],迭代次数搜索范围[10, 200],输入批量搜索范围[128, 1 024],学习率搜索范围[10-5, 10-2];最大训练轮数设为100。 训练过程中,利用SSA优化算法不断地调整LSTM中神经元个数、迭代次数、输入批量和学习率4个模型参数,预测结果的平均绝对百分比误差作为麻雀适应度,当适应度连续3轮没有变化时训练停止。优化结果如表2所示,训练16轮时达到最优适应度。 表2 SSA-LSTM优化结果 根据SSA优化结果设置LSTM模型参数,对日光温室空气温湿度、光照强度、CO2浓度及土壤温湿度分别进行未来21 d预测,预测结果如图9所示。 图9 基于SSA-LSTM的温室环境预测结果 为了更好地验证SSA-LSTM模型在多维温室环境数据预测中的优越性,同时利用BP神经网络、LSTM及 GRU模型对温室环境预测并对比分析。在相同运算环境的输入参数条件下,4种模型环境预测性能的对比如表3所示。 由表3可知,采用SSA-LSTM模型对温室空气温湿度、土壤温湿度、CO2浓度和光照强度6种参数进行预测,对空气温度预测拟合指数最高,为98.2%,平均绝对百分比误差为2.5%,均方根误差为0.6℃;受人工灌溉等因素影响,对土壤相对湿度预测拟合指数相对偏低,为96.8%,其MAPE为3%,RMSE为0.7%。 表3 4种模型预测性能对比 采用了SSA自动进行参数选优方式的SSA-LSTM,使模型预测性能发挥到极致,SSA-LSTM的平均MAPE降低至2.7%,相比BP、GRU、LSTM分别降低6.3、3.2、3.4个百分点;BP、GRU、LSTM和SSA-LSTM拟合指数分别为89.5%、93.5%、93.3%和97.6%,对比其它3种模型,SSA-LSTM预测拟合指数分别提升8.1、4.1、4.3个百分点,模型预测性能最佳。 (1)针对农业物联网数据体量大、维数爆炸、计算成本高,传统的LSTM在训练过程中依靠人工经验手动调节参数,处理高维数据时收敛速度慢且容易陷入局部最优等问题,本文提出一种基于SSA优化的LSTM温室环境预测模型,实现了温室空气温湿度、土壤温湿度、CO2浓度及光照强度6种环境数据的精准预测。 (2)与BP神经网络、GRU及LSTM模型进行温室环境预测对比分析。实验结果表明:BP、GRU、LSTM和SSA-LSTM拟合指数分别为89.5%、93.5%、93.3%和97.6%,SSA-LSTM的拟合效果明显提升。证明本研究提出的SSA-LSTM模型在温室环境数据预测中具有较高的优越性。2.2 长短期记忆人工神经网络

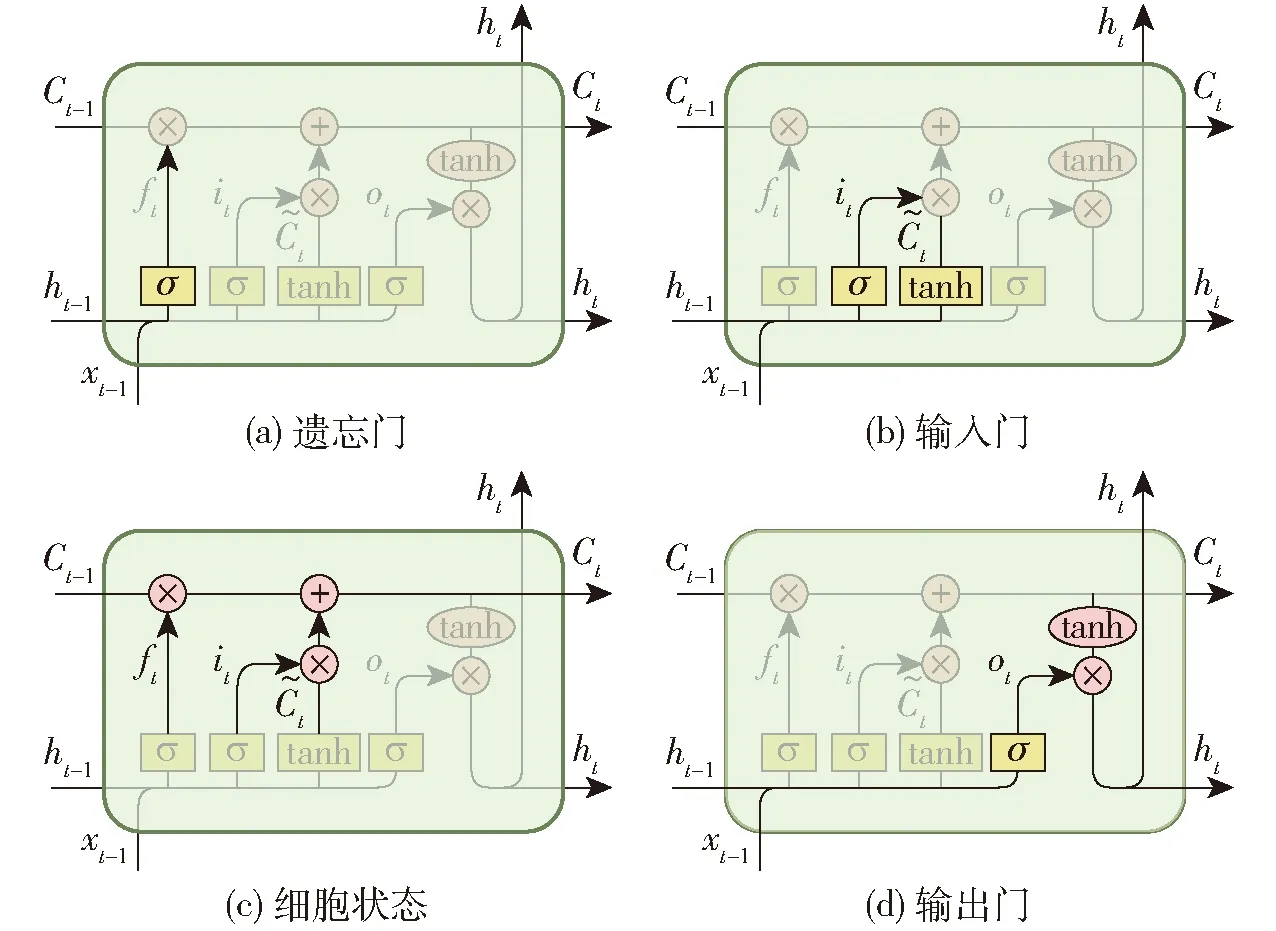
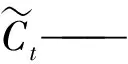
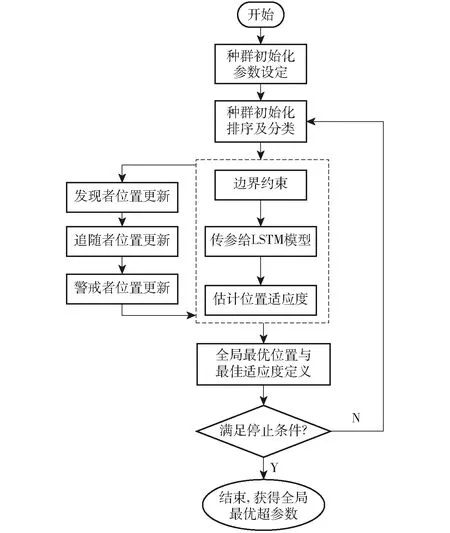
2.3 SSA优化的LSTM温室环境预测模型
2.4 模型评价指标
3 实验结果与分析
3.1 实验平台
3.2 SSA-LSTM模型优化及训练

3.3 预测结果及对比分析

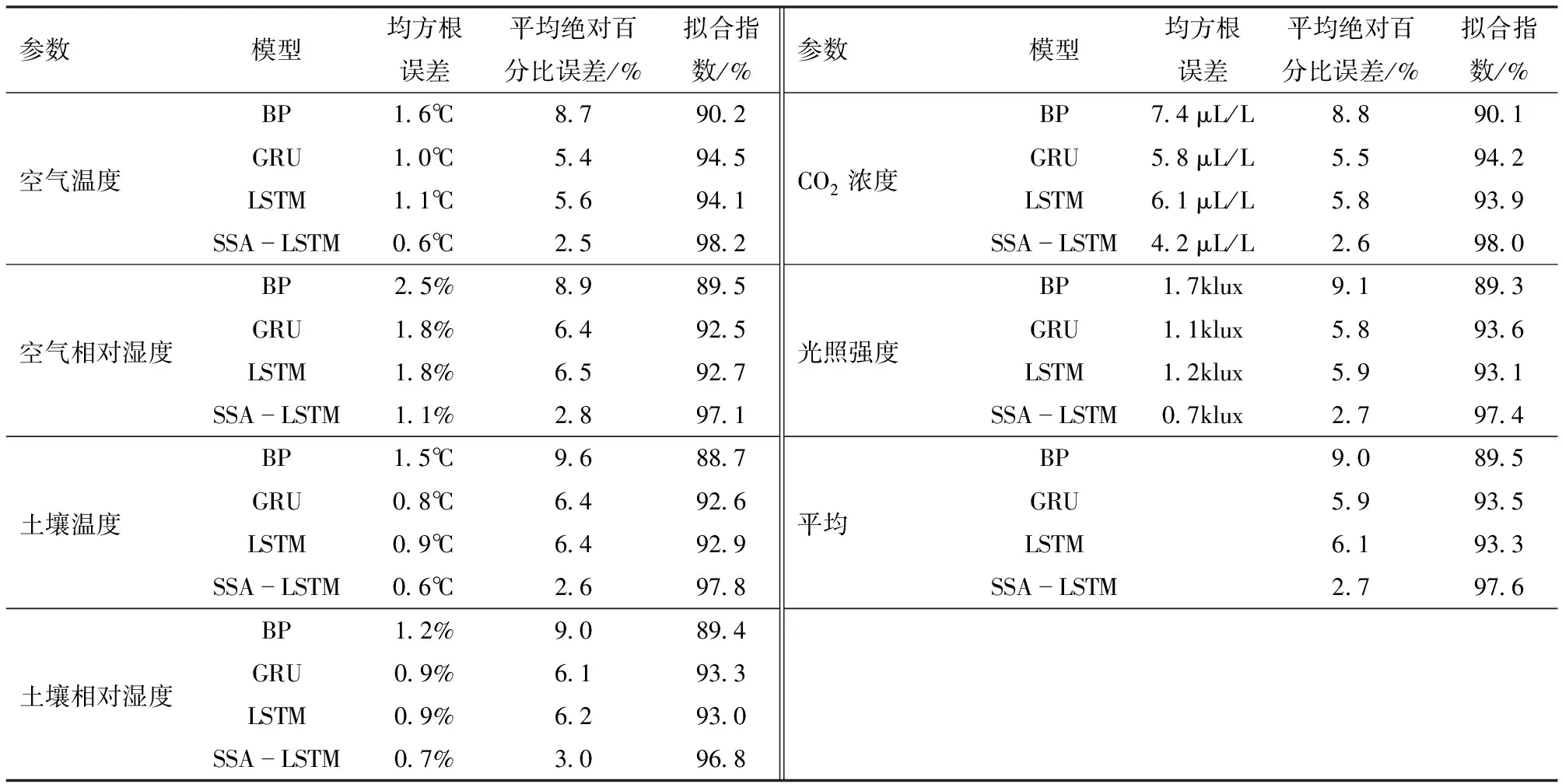
4 结论

