圆锥盘推板式水田侧深施肥双行排肥器设计与试验

王金峰 付佐栋 翁武雄 王震涛 王金武 杨东泽

(东北农业大学工程学院，哈尔滨 150030)

0 引言

化肥是保障农作物丰产的重要生产资料，但过度施肥造成土壤酸化板结、施肥不均匀导致农作物吸收不充分等问题[1]。相关研究表明，精准施用化肥能够提高肥料利用率、减轻环境污染。水田侧深施肥技术可将肥料定位、定量、均匀地施于秧苗侧3.0～5.0 cm，深4.0～5.0 cm处，是最高效和环保的一种施肥方式[2]，是实现节本增效和提高作业效率的重要方法，目前已被广泛应用[3-4]。

排肥器是侧深施肥装置的核心部件，排肥性能直接影响施肥作业的质量。目前，国内外研究的排肥器形式主要有外槽轮式、螺旋式、圆盘式等。外槽轮式排肥器是最常见的施肥装置，已进行了大量研究，如祝清震等[5]探究了外槽轮结构参数对直槽轮排肥器排肥均匀度的影响规律，通过正交试验得出了最佳组合参数；王金峰等[6]和杨洲等[7]将直槽式排肥轮改进为螺旋式排肥轮，分别探究了槽轮转速与螺旋升角等对排肥均匀性和排肥量的影响；DU等[8]设计了一种交错排列式螺旋齿排肥轮，与直槽轮的对比试验表明交错排列式螺旋齿排肥轮提高了排肥均匀性与稳定性；SUGIRBAY等[9]设计了一种新型外槽轮结构，改善了外槽轮低转速下排肥均匀性差的现象。螺旋式排肥器是一种利用螺旋体与肥料之间产生的相对运动输送肥料的装置，陈雄飞等[10]设计了一种两级螺旋排肥装置，建立了排肥螺旋单圈排肥量数学模型，通过试验验证了排肥装置肥量施用的准确性与稳定性。圆盘式排肥器是一种通过在水平面内旋转的刮板带动肥料运动排出的强排装置，目前只有洋马公司生产的侧深施肥装置上采用这种排肥器，可通过更换不同孔径排肥盘与调节排肥盘转速控制施肥量，具有良好的均匀性，但其结构复杂，肥量调节繁琐，长时间作业时肥料易在较小的充肥区粘结，降低排肥性能[11-12]。现阶段水田侧深施肥装置主要采用外槽轮式，但存在低转速下脉动性强和排肥量调节范围小等问题；螺旋式排肥器因工作特性导致对肥料作用力较大，应用于水田存在一定局限性；而圆盘式排肥器具有良好的排肥均匀性，因此，设计一种圆盘式排肥器，实现排肥均匀和肥量调节稳定，可对水田侧深施肥装置性能提升起到重要支撑作用。

为满足黑龙江寒地稻作区侧深施肥农艺要求，提高水田复杂环境下排肥器的均匀性、稳定性及肥量调节能力，本文以侧深施肥专用肥为研究对象，在保证足够充肥空间的前提下设计一种充肥流畅、排肥平稳的圆锥盘推板式双行排肥器，阐述排肥器工作原理，对主要工作部件进行理论与仿真分析，通过台架试验探究圆锥转盘转速、排肥口开度与排肥量和排肥性能之间的关系，以期为水田侧深施肥装置研究与技术推广提供参考。

1 排肥器结构与工作原理

圆锥盘推板式双行排肥器主要包括：导肥箱、扰肥杆、上壳体、圆锥转盘、下壳体、挡肥叶片、调节板、锁定螺母、托板、排肥管等结构。按排肥器实际工作过程可划分为充肥区、导肥区、排肥区及过渡区4个区域，为提高工作效率，排肥器对称设置两个排肥口，因此每个区域对应分为两部分。导肥箱设置在上壳体正上方以保证两侧肥料同步下落，将转盘设计为圆锥状，有利于肥料填充，增强肥料流动性，避免肥料成拱，同时利用扰肥杆对肥料进行扰动。排肥器分解图与4个功能区域如图1所示。

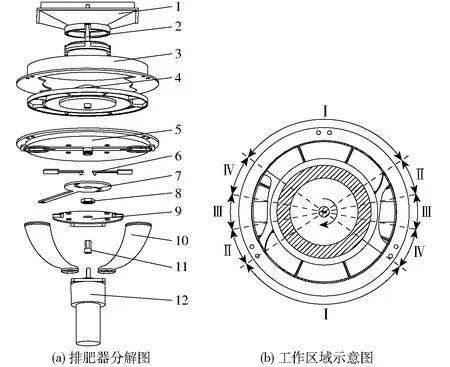
图1 排肥器结构与工作区域

圆锥盘推板式双行排肥器由电机驱动工作，肥料通过导肥箱沿顺时针旋转的圆锥转盘下滑至充肥区推板间隔内完成填充，在推板作用下进一步运动至由上壳体弧形挡板遮挡的护肥区，于下壳体两个排肥区被推送到排肥管内，最后在外部气流作用下快速吹出完成作业。排肥量可通过转动调节板控制挡肥叶片伸出长度进而改变排肥口有效作业面积进行调节。

2 排肥器关键结构设计

2.1 圆锥转盘设计

圆锥盘推板式双行排肥器主要工作部件为圆锥转盘，其设计参数将直接影响排肥性能。圆锥转盘结构如图2所示。

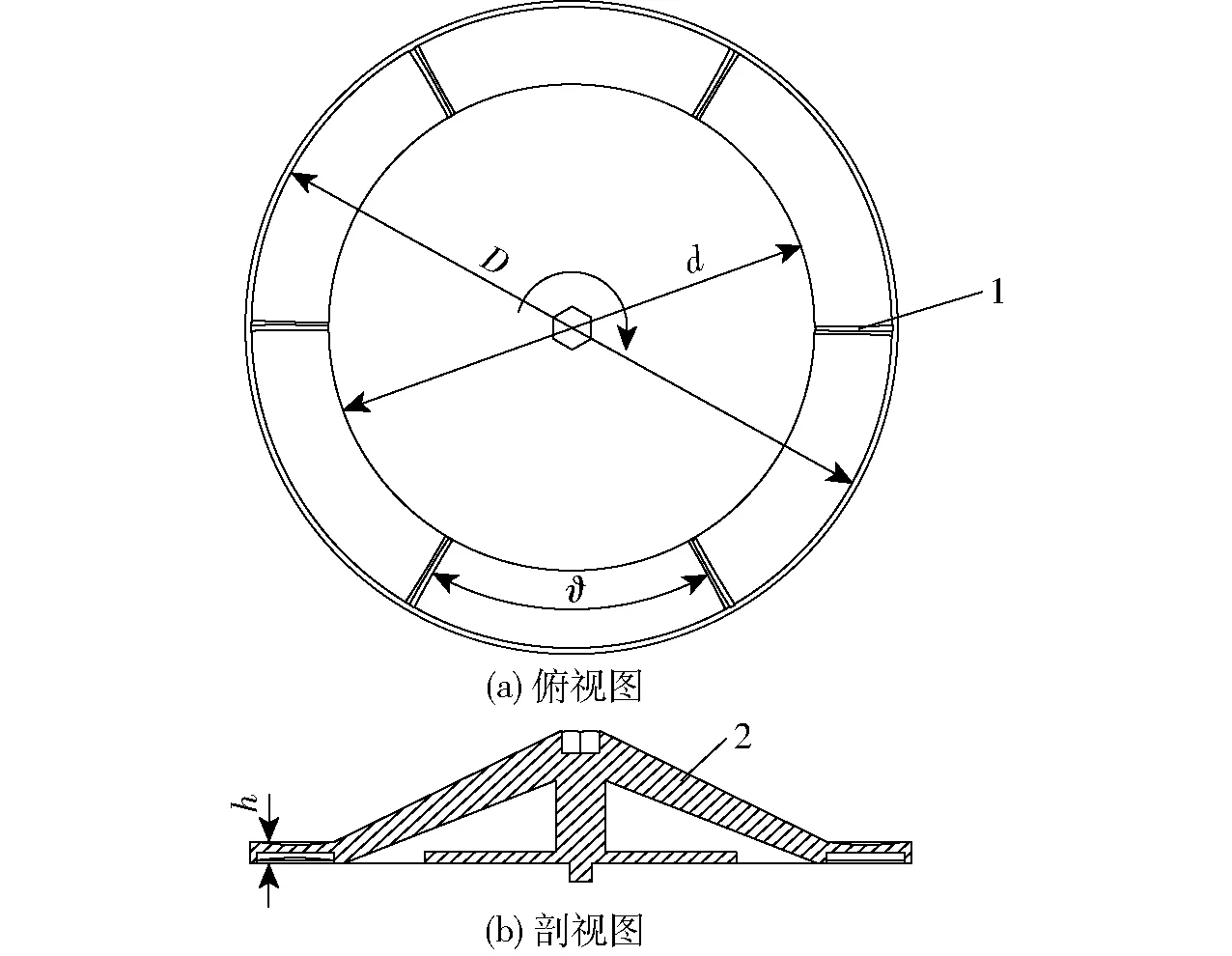
图2 圆锥转盘结构参数示意图

2.1.1排肥速率

排肥速率是排肥器设计的主要参考依据，其受肥料填充系数、排肥器结构尺寸、肥料物理特性等因素影响[13]。为满足作业效果，需保证理论排肥速率的准确性。选取中化集团有限公司生产的水稻侧深施肥专用肥作为研究对象，测得肥料体积密度为0.86 g/cm3，由于挡板较薄，忽略其所占体积，假设不考虑排肥时空气阻力作用，排肥速率计算式为

(1)

式中q——排肥器排肥速率，g/min

D——圆锥转盘水平外径，m

d——圆锥转盘水平内径，m

h——圆锥转盘水平高度，m

n——圆锥转盘转速，r/min

φ——填充系数

ρ——缓释肥体积密度，g/m3

排肥器实际工作时，根据水田侧深施肥总施肥量150～930 kg/hm2的农艺要求，排肥速率为

(2)

式中qn——农艺要求排肥速率，g/min

Q0——农艺要求水田侧深施肥量，kg/hm2

L——作业幅宽，m

v——施肥作业速度，m/s

Z——排肥器个数

农艺要求排肥速率与排肥器排肥速率相等，结合式(1)、(2)可得

(3)

侧深施肥排肥器通常搭载在6行高速插秧机上进行田间作业，常规作业速度为1.0～1.6 m/s，作业幅宽为1.8 m[14-15]。插秧机机型、前进速度及肥料物理特性确定后，即L、Z、v、ρ一定，由式(3)可知，排肥量主要与D、d、h、n有关。其中转速是排肥器性能的重要影响因素，具有一定合理范围，因此在确定排肥器相关结构尺寸时，需同时兼顾圆锥转盘转速。综合考虑排肥器空间位置尺寸、肥料粒径与内外径差值从而提高肥量调节范围，确定圆锥转盘水平外径D为208 mm，水平内径d为158 mm，水平高度h为7.5 mm。

2.1.2圆锥转盘推板设计

推板具有扰动与推送肥料作用，可减轻肥料在圆锥转盘底部粘结堵塞现象，是排肥器主要工作部分。当每转排肥量和转速一定时，推板数量N不仅影响肥料在相邻推板之间的填充特性，同时决定着排肥器工作性能。

为保证排肥连续稳定，应使肥料填充流畅且任意时刻的推板推力能将肥料顺利排出。推板数量少，相邻推板间隔空间增大，肥料填充时相对移动距离增加，有利于肥料填充；同时排肥阶段肥料间流动性增强，降低了肥料与排肥器间作用力，减轻肥料破碎现象[16]。但随着推板数量的减少，推板间隔两侧肥料运动状态差别增大，引起排肥稳定性、均匀性的变化。由于排肥器设计为双行供肥，因此设计推板数量为偶数以同步两个排肥口的排肥性能。推板任意时刻对排肥区肥料应存在肥料流向方向的分力，保证连续推送作用，即相邻两个推板夹角ϑ≤90°，则推板数量N应满足

N≥4

(4)

基于物料流动特性[17]，推板间隔至少满足物料颗粒等效直径的6倍从而达到流动物料运动条件，即

ld>6df

(5)

式中ld——推板间隔内侧弧长，mm

df——肥料等效直径，取3.4 mm

在满足上述条件下，减少推板数量能够提高推板间隔内肥料流动性以及排肥连续性，因此初步设计圆锥转盘推板数量为6。

2.1.3圆锥转盘转速

圆锥转盘转速是影响排肥器性能的主要因素之一，施肥量满足农艺要求条件下，合理的转速有利于提高排肥性能。肥料在圆锥转盘上运动过程中，相邻肥料之间存在的相互作用力Fq随时变化，但肥料颗粒尺寸相对较小，相邻肥料之间运动条件近似相同，对于单个颗粒所受相互作用力可近似抵消[18]，因此忽略Fq影响。假设肥料颗粒获得与转盘相同的角速度，不考虑空气阻力影响，肥料在圆锥转盘上任意时刻受力如图3所示。

图3 肥料在圆锥转盘上的受力分析

肥料颗粒随圆锥转盘转动的同时沿锥面母线下滑，速度方向时刻改变。根据达朗贝尔原理，肥料颗粒受力方程为

(6)

式中m——肥料颗粒质量，g

Fc——肥料颗粒科氏力，N

FN——圆锥转盘对肥料颗粒支持力，N

G——肥料颗粒重力，N

Fr——肥料颗粒离心力，N

Ff——肥料颗粒摩擦力，N

Ffx——肥料颗粒x方向摩擦力，N

Ffy——肥料颗粒y方向摩擦力，N

Fax——肥料颗粒x方向惯性力，N

Fay——肥料颗粒y方向惯性力，N

vr——肥料颗粒沿x方向运动速度，m/s

ax——肥料颗粒x方向加速度，m/s2

ay——肥料颗粒y方向加速度，m/s2

ω——圆锥转盘角速度，rad/s

θ——圆锥转盘倾角，(°)

β——摩擦力与x轴夹角，(°)

R——肥料颗粒回转半径，m

μ——肥料颗粒与圆锥转盘的摩擦因数

当肥料颗粒在x轴正方向合力大于零时，具有沿x轴正方向的加速度，可增强肥料填充性能并减少填充时间[19]，即ax>0，化简式(6)，可得

(7)

肥料颗粒下滑填充过程中，应时刻与圆锥转盘接触，避免因转速过快造成肥料飞溅，即FN≥0，化简式(6)得

(8)

式中H——圆锥转盘高度，m

根据式(7)可知，满足ax>0条件的最小转速与肥料颗粒和PLA塑料圆锥转盘之间的滚动摩擦因数μ、圆锥转盘倾角θ、摩擦力与x轴夹角β以及肥料颗粒在圆锥转盘上的回转半径有关。对于同一种肥料，转速临界值随着肥料颗粒回转半径的增大而减小，其范围由圆锥转盘倾角决定。由式(8)可知，圆锥转盘最大转速仅与高度H有关(圆锥转盘半径确定条件下，与圆锥转盘倾角θ视为同一变量)。相关研究表明，颗粒下落至锥面发生的涌动现象与下落高度和锥面倾角有关[20]，下落高度越高即相对圆锥转盘高度越低，H过低肥料颗粒虽可以顺畅下落，但在撞击锥面动能损失后易在底部形成堆积，不利于肥料填充；H过高导致肥料颗粒在圆锥转盘顶部卡滞堵塞，造成肥料破损的同时增加了肥料下滑时间。圆锥转盘倾角需大于肥料自然休止角[21]，根据前期试验所得肥料堆积角为26.45°，综合空间尺寸将圆锥转盘倾角θ设计为28°，此时圆锥转盘高度H为42 mm。将圆锥转盘高度H代入式(8)中，计算得ω≤15.3 rad/s，即圆锥转盘理论最大转速n为146 r/min。

为进一步研究圆锥转盘转速对排肥性能的影响，同时确定圆锥转盘最低转速，分别分析处于导肥阶段与排肥阶段肥料颗粒力学与运动学特性。首先对导肥区推板间隔肥料进行定性分析，如图4中区域b所示，在y轴方向上满足

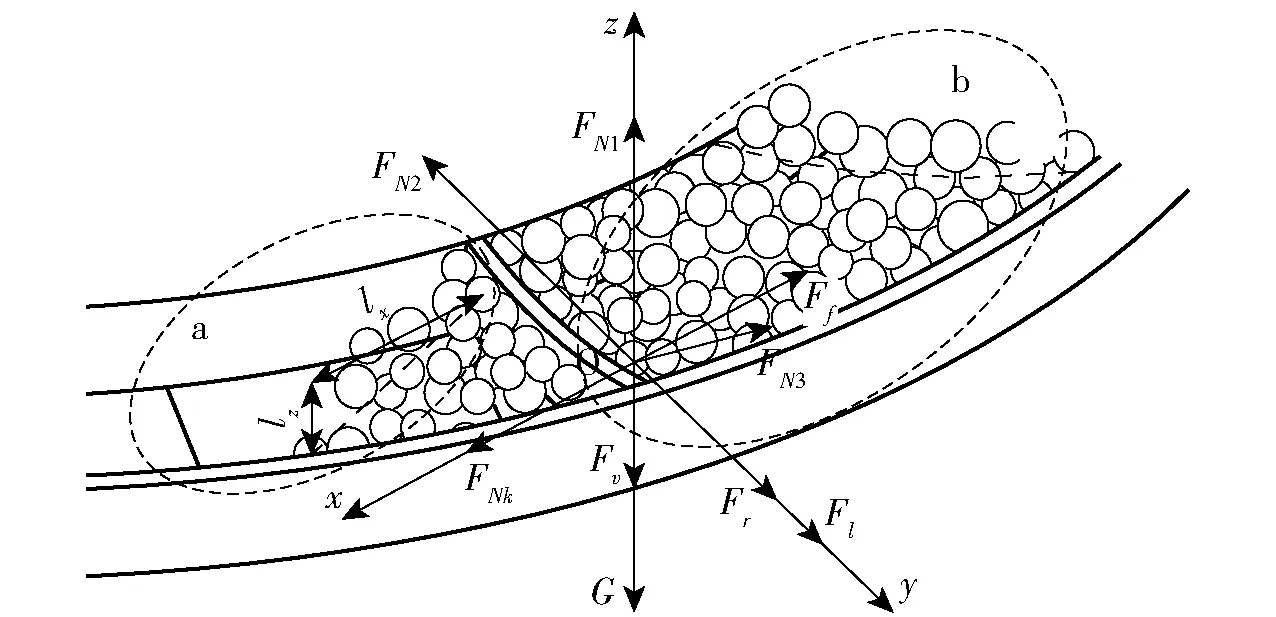
图4 导肥、排肥过程肥料模型

FN2-Fl-Fr=0

(9)

式中Fl——上层肥料颗粒的水平压力，N

FN2——圆锥转盘外环对肥料颗粒支持力，N

肥料在推板间隔内符合农业物料学中浅仓模型条件[22]，即

(10)

式中K——压力比

Fv——上层肥料颗粒垂直压力，N

φi——内摩擦角，(°)

γ——重度，kN/m3

zh——肥料深度，m

结合式(9)、(10)可得

(11)

由式(11)可知，圆锥转盘外环对肥料颗粒支持力与圆锥转盘转速呈正相关，正常作业时应降低转速减小支持力，从而减小肥料受力、减轻圆锥转盘外侧肥料堆积现象，保证肥料颗粒在排肥区流畅下落。

如图4区域a所示，根据排肥连续性条件对该区域肥料进行运动学分析，确定圆锥转盘最慢转速。肥料离开排肥区时做平抛运动，在xoz平面内位移模型为

(12)

式中lx——肥料颗粒横移距离，m

lz——肥料颗粒下落高度，m

vk——肥料颗粒速度，m/s

t——肥料颗粒运动时间，s

为保证肥料连续排出，肥料颗粒下落单位颗粒直径长度时，横移距离应大于肥料单位直径长度与推板厚度(1 mm)之和的距离。将满足上述条件的各参数代入式(12)，计算得ω=1.4 rad/s，即圆锥转盘最小转速n为13 r/min。

由上述分析可知，圆锥转盘极限转速为13～146 r/min，在此范围内降低工作转速有利于肥料流动，减轻肥料颗粒因碰撞挤压而产生的破碎现象。由式(3)可知，排肥器结构尺寸确定后，根据最大农艺施肥量要求及肥料填充系数，圆锥转盘转速达到42 r/min时，即可满足农艺要求的最大施肥量930 kg/hm2。由于施肥量随转速增加而增加，超过该转速时，施肥量超过农艺要求的最大施肥量，因此，确定圆锥转盘转速范围为15～45 r/min。

2.2 挡肥叶片设计

按设计需求，挡肥叶片宽度与下壳体排肥口宽度应保持一致，宽度过小时，肥料颗粒以一定角速度经过排肥区会出现未及下落便被推送至过渡区的现象；宽度过大时，增加肥料颗粒在挡肥叶片上的运动时间，降低排肥稳定性，且间接减小了充肥区有效范围，影响肥料填充。图5为肥料在下壳体排肥口处运动分析简化图。

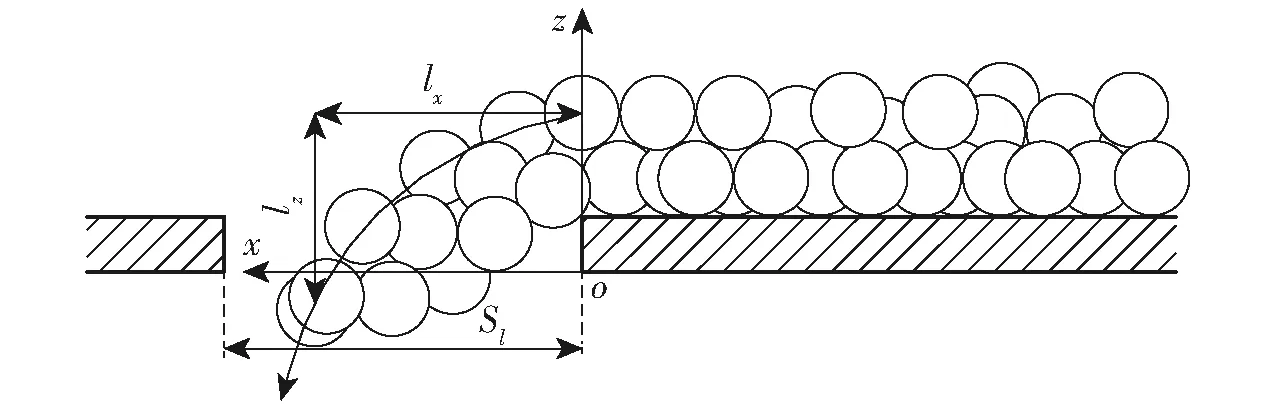
图5 下壳体排肥口肥料运动分析

排肥口宽度Sl取值由圆锥转盘最大转速决定，圆锥转盘以最大转速(45 r/min)工作时，根据运动学分析可得

(13)

式中vmax——理论最大速度，m/s

根据式(13)可得

(14)

为保证肥料颗粒能够正常排出，下壳体排肥口宽度Sl应大于肥料竖直方向下落圆锥转盘水平高度h与下壳厚度(3.5 mm)之和距离所需时间内，肥料以最大转速排出的水平位移lx，将上述条件值代入式(14)可得lx≈23.2 mm，综合考虑设计余量与下壳体排肥口宽度要求，将Sl(即挡肥叶片宽度)设计为25 mm。

2.3 排肥管设计

肥料在排肥区排出后沿排肥管滑落，利用最速降线性质设计排肥管纵向截面曲线可加速肥料下滑，缩短运动时间，最速降线参数方程为

(15)

式中k——常数ψ——参变量

其中，k是影响曲线曲率的主要参数，根据排肥口与文丘里管入口横向相对尺寸，确定最速曲线方程为

(16)

3 离散元模型建立与仿真

为研究圆锥转盘上推板数量对圆锥盘推板式双行排肥器性能的影响规律，确定最佳推板数量，在理论分析基础上利用离散元软件EDEM 2018对设置有不同推板数量的圆锥转盘进行仿真分析。

3.1 排肥器模型建立

使用Creo 5.0软件建立圆锥盘推板式双行排肥器三维模型(比例1∶1)，删除肥箱及与肥料颗粒无接触部件简化仿真计算量，其余模型以.stl格式导入EDEM软件中，选用merge命令将圆锥转盘与扰肥立柱模型组合，如图6所示。根据3D打印PLA材料属性设置排肥器模型属性参数[12]，泊松比为0.29，剪切模量为2.2×108Pa，密度为1 110 kg/m3。

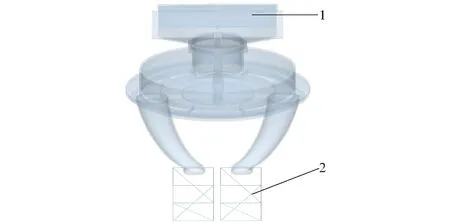
图6 排肥器仿真模型

3.2 肥料模型建立与仿真参数设置

水稻侧深施肥专用肥料颗粒为类球状，当肥料颗粒球形比大于90%时，可直接选择单个球形模型进行模拟[23]，根据前期试验与文献[14]，肥料等效直径满足正态分布规律，肥料基本物理参数及相互接触参数如表1所示。

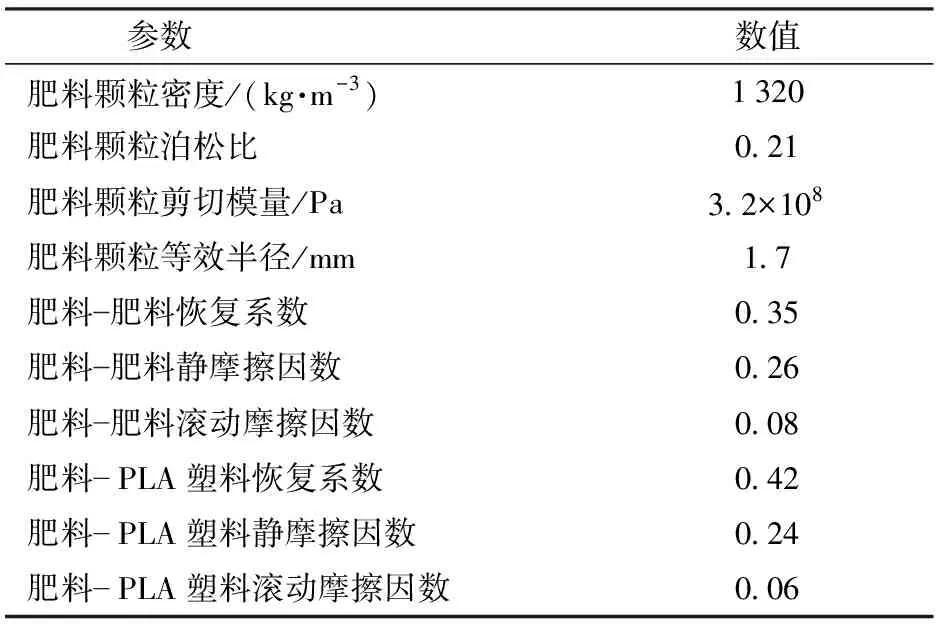
表1 肥料颗粒模型物理特性及接触参数

由于肥料颗粒、PLA塑料表面无黏附作用，接触模型均选用Hertz-Mindlin无滑动接触模型。为减少颗粒生成数量以节省仿真时间，设置颗粒生成速度为18 000粒/s，总生成量为12 000粒，颗粒起始下落速度为100 mm/s。

3.3 虚拟仿真试验设计与评价方法

基于上述分析，为确定最合适的推板数量，根据前期仿真预试验结果，在转速为35 r/min、排肥口开度为25 mm条件下，开展推板数量对肥料填充特性定性分析与排肥性能定量分析的单因素影响试验，推板数量分别设置为4、6、8、10、12。肥料颗粒填充特性通过其在推板间隔内的动能衡量，动能相差越大，肥料填充越不均匀，导致排肥性能降低。在EDEM模拟试验中，为了准确表示不同推板数量对排肥性能的影响规律，采用质量流量变异系数评价排肥性能[24]。通过添加Geometry Bin Group输出每个节点的质量，计算一段时间内所测得的肥料流量均匀性，变异系数越大，表明排肥器均匀性越差。

3.4 虚拟仿真过程与结果分析

在虚拟作业过程中，设置固定时间步长为1.81×10-6s，即Rayleigh时间步长的20%，总仿真时长5.5 s，每0.01 s保存一次仿真数据，单元网格尺寸设置为颗粒平均半径的3倍。

3.4.1不同推板数量对肥料填充特性的定性分析

利用EDEM软件后处理Selection模块中Imported Geometry Bin Group功能，导入内径为150 mm、外径为220 mm、厚度为9 mm、圆心角为100°的.stl格式模型文件监测一侧充肥区肥料的动能分布情况，添加Clipping Planes以便直观显示仿真结果。在排肥器达到稳定工作状态后，截取不同推板数量的圆锥转盘任一推板转至距离导肥区相同位置时充肥区的动能分布图，如图7所示。

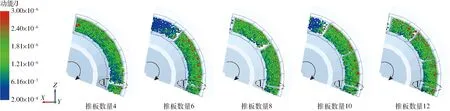
图7 充肥区肥料动能分布

由图7可知，在圆锥转盘转速一定时，推板数量对肥料填充特性有明显影响(图中蓝色、绿色、红色代表肥料颗粒动能依次增加)。当推板数量为4时，单个推板间隔内临近排肥区一端肥料动能小于远端动能的现象明显，且区域I内靠近推板处存在肥料填充空隙，影响排肥性能；推板数量从4增至12过程中，单个推板间隔内肥料颗粒动能逐渐趋于一致，表明肥料颗粒状态相对稳定，分布逐渐均匀；当推板数量大于等于8时，区域I内肥料填充空隙消失，证明肥料具有较好的填充特性。分析产生上述结果原因为：当推板数量较少时，推板间隔变大，肥料虽易填充，但肥料之间所传递的推板作用力降低，造成间隔两端肥料分布不均，与前述理论分析一致。

3.4.2推板数量对排肥性能的定量分析

不同推板数量对肥料质量流量变异系数影响如图8所示，两个排肥口肥料质量流量变异系数随推板数量的增加均呈先减小后增大的变化规律，表明推板数量过少或过多均会降低排肥作业性能，在推板数量为8时同时取得最小值，且排肥口1与排肥口2变异系数差值最小，证明当推板数量为8时排肥器具有最佳工作性能。

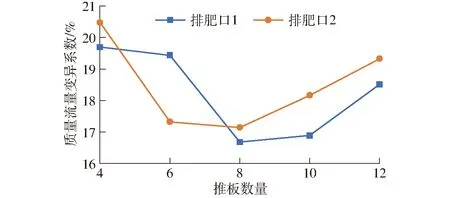
图8 不同推板数量下排肥性能变化曲线

综合推板数量对肥料填充特性及质量流量变异系数影响规律，最终确定推板数量8作为圆锥转盘最佳结构参数。

4 圆锥盘推板式排肥器台架试验

4.1 试验条件

基于上述圆锥转盘参数优化结果，以中化集团有限公司生产的水稻侧深施肥专用肥为试验材料，于东北农业大学排种实验室，应用JPS-12型排种器性能检测试验台进行排肥器性能试验。排肥器整体结构由3D打印机加工成型，除施肥系统主要装置外，试验仪器有电子秤精度0.01 g和肥料收集毛刷，台架试验装置如图9所示。

图9 施肥系统台架试验装置

4.2 试验指标与测定方法

施肥试验时，采用两因素试验方法，以圆锥转盘转速和排肥口开度为试验因素，因素水平如表2所示。以平均排肥量y1、双行排肥量一致性变异系数y2、总排肥量稳定性变异系数y3、排肥均匀性变异系数y4为试验指标，分别研究排肥量、排肥稳定性、均匀性变异系数与圆锥转盘转速、排肥口开度之间的线性关系。参照文献[25]进行各项性能试验与测定。排肥均匀性测定为动态试验，由于胶带加速到1 m/s需要一定时间，因此，试验时待胶带运行稳定后将间隔为100 mm、长度为4 000 mm的肥料收集袋放置于传送带上，直至其完全通过排肥器下方时停止胶带转动，收集测量各间隔内肥料质量后仅将后30段间隔数据用于排肥均匀性变异系数的计算；其余性能试验单次测试时间为10 s[24]，排出的肥料收集在一个收集袋中，并在电子秤上称量。

表2 试验因素与水平

4.3 试验结果与分析

试验设计与收集计算后所得各指标如表3所示。

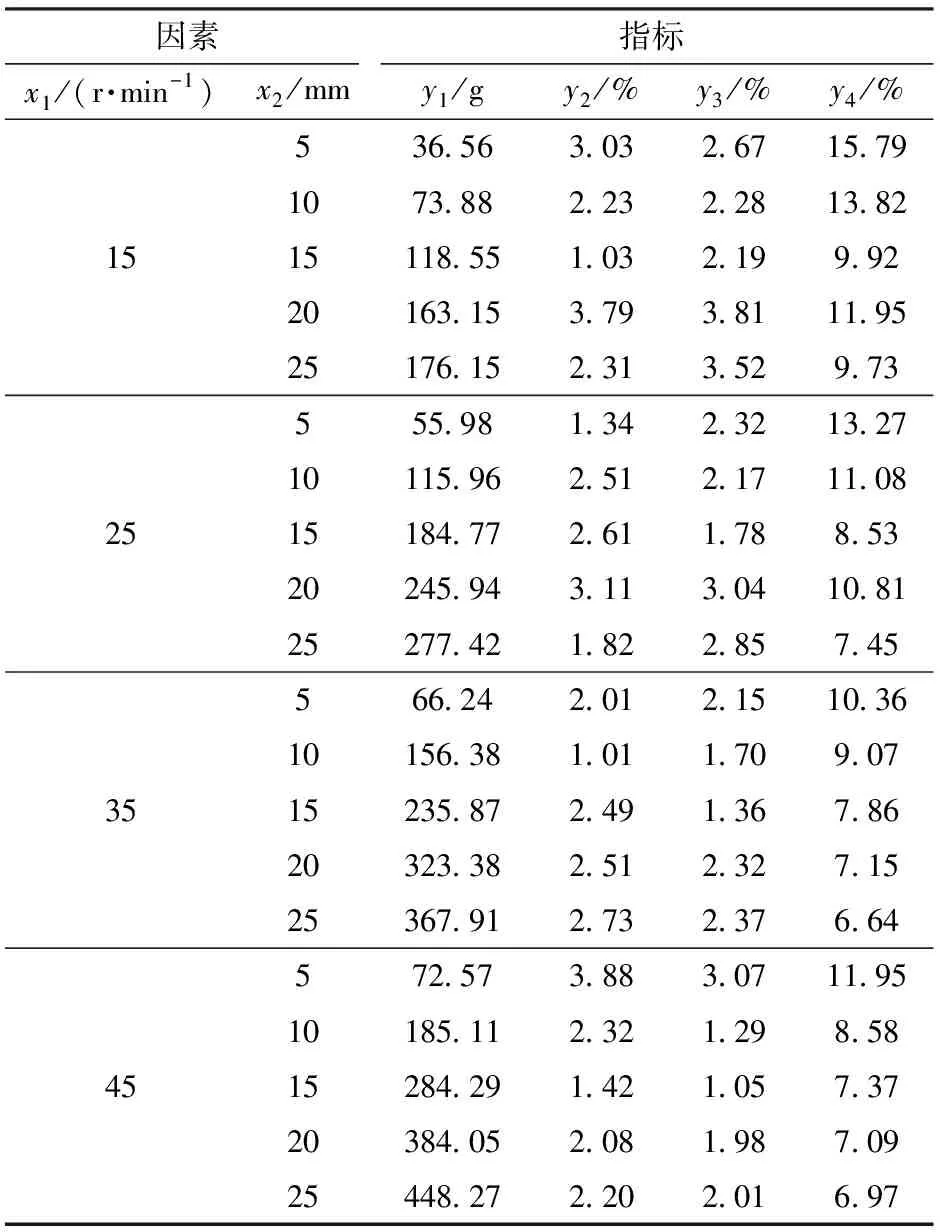
表3 试验设计与结果

4.3.1排肥量相关性

对不同条件下排肥器单侧平均排肥量进行线性拟合，建立了排肥量y1与圆锥转盘转速x1、排肥口开度x2的回归方程。分别计算不同条件下的决定系数R2，对相应线性关系进行分析，结果如表4、5所示，相应散点图如图10、11所示。

表4 不同开度排肥量与转速回归方程及决定系数

由表4与图10可知，排肥口处于不同开度排肥量与转速之间均呈良好的线性关系，排肥量随转速的增加而增加，转速与排肥量拟合的线性决定系数R2随排肥口开度增加整体呈上升趋势，说明排肥量与转速的线性相关性增强，最小值为0.989 2，最大值为0.999 2。因此，可通过调节圆锥转盘转速调节排肥量。图10显示在不同开度下，试验点在低转速时位于拟合曲线下方，随着转速的增加沿拟合曲线向上移动最后下降，但浮动范围较小。分析原因为随着转速的增加，推板间隔内肥料的填充系数降低，导致排肥量变化。

图10 不同开度排肥量与转速关系曲线

由表5与图11可知，不同圆锥转盘转速下排肥量与排肥口开度均呈良好的线性关系，排肥量随开度的增加而增加，排肥口开度与排肥量拟合的线性决定系数R2随转速的增加整体呈上升趋势，说明排肥量与排肥口开度的线性相关性增强，最小值为0.976 3，最大值为0.993 6，因此也可通过调节排肥口开度调节排肥量，但其决定系数普遍低于排肥量与转速之间的决定系数，说明通过调节转速可更精确调节肥量。图11显示在不同转速下，试验点均呈现排肥口开度小时位于拟合曲线下方，随着开度的增加沿拟合曲线向上移动最后下降的趋势；在开度为20 mm时，试验点偏移量最大，结合上述排肥量与转速试验结果，分别如表4与图10所示，x2=20 mm时，决定系数R2最小，且拟合曲线偏离开度为25 mm一侧，分析原因为随着排肥口开度的增加，挡肥叶片有效工作面积逐渐减小，上方流过的肥料颗粒塌陷现象逐渐增强[26]，导致肥料排出量多于理论值，直至排肥口处于完全工作状态。

表5 不同转速排肥量与开度回归方程及决定系数

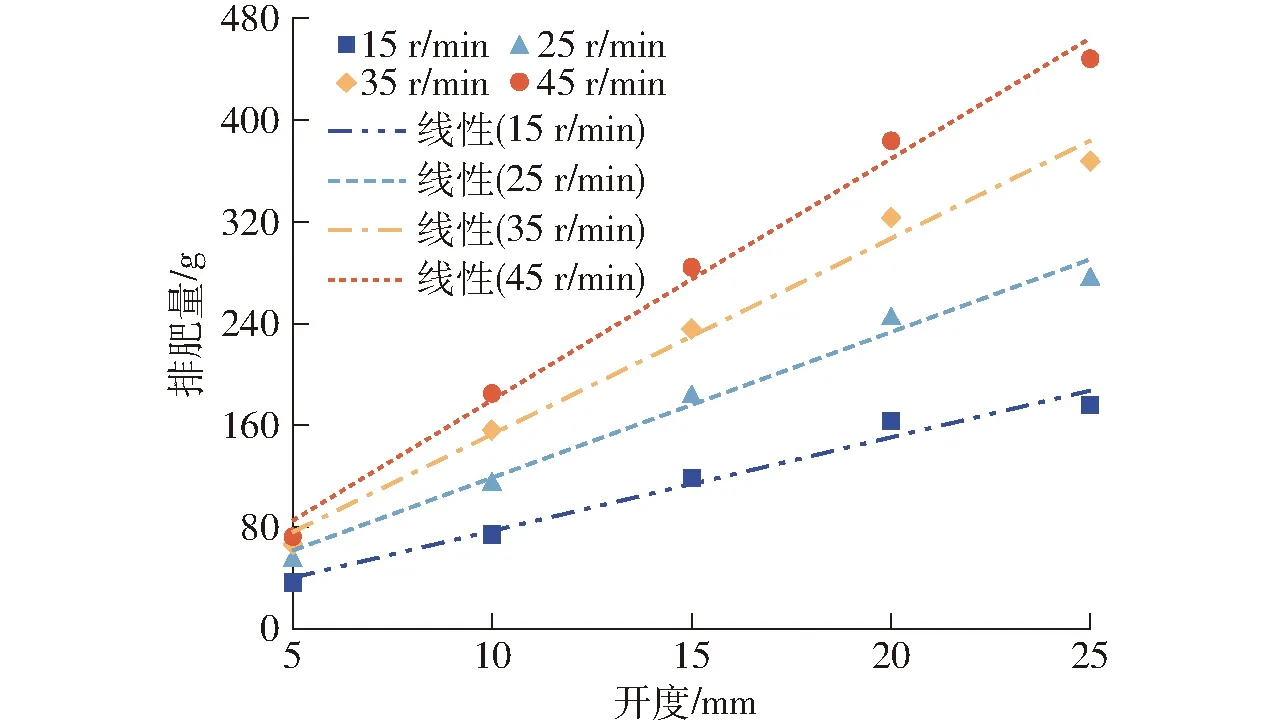
图11 不同转速排肥量与开度关系曲线

综合排肥量试验结果，排肥器转速为15～45 r/min，排肥口为5～25 mm调节范围内，排肥量范围为122～934 kg/hm2，可满足机具常规作业速度1.0～1.6 m/s时农艺要求150～930 kg/hm2的施肥量。

4.3.2排肥器性能参数

在Design-Expert 6.0.10软件中对排肥器性能试验结果进行多因素分析。

圆锥转盘转速和排肥口开度对双行排肥量一致性变异系数y2影响不显著，结果如图12所示。由图12可知，y2max为3.88%，y2min为1.01%，最大值满足文献[25]中各行排肥量一致性变异系数小于等于13%的要求。

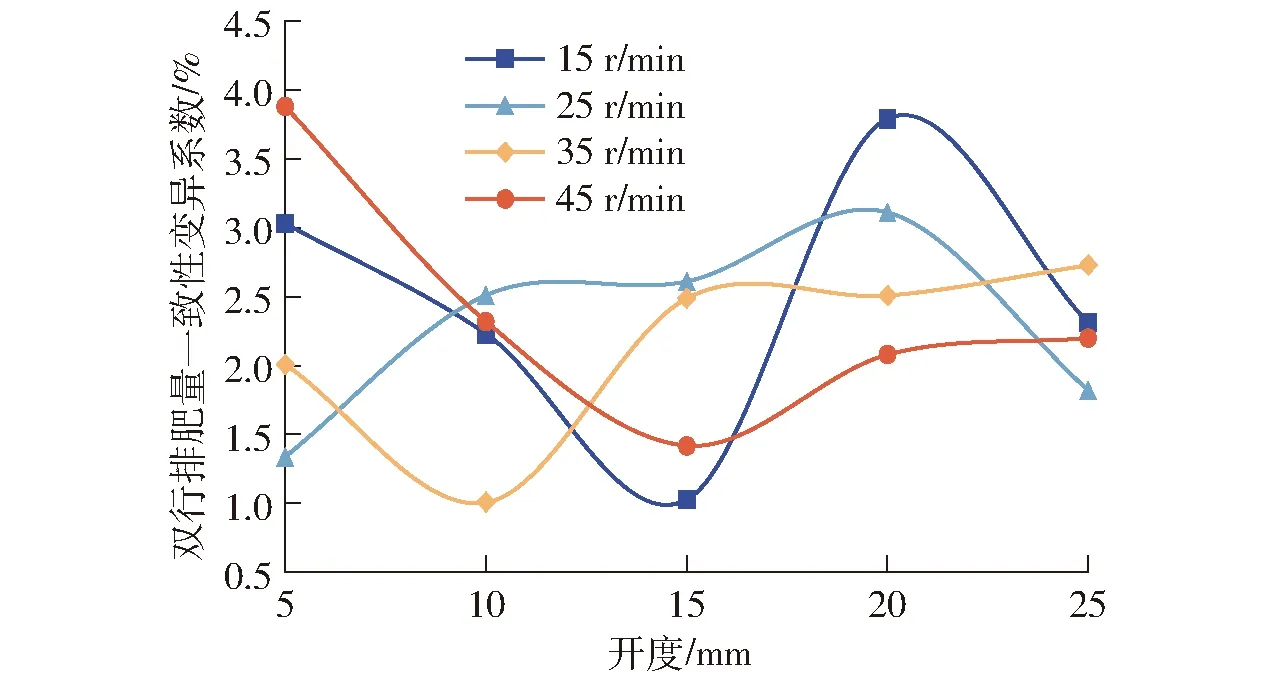
图12 双行排肥量一致性变异系数变化曲线

由于水田作业环境复杂，排肥器无法始终保证水平作业状态，导致两个排肥口排肥量存在差异，因此进行排肥器在一定倾角下的双行排肥量一致性试验。根据水田搅浆平整地后高度差与东北地区常用插秧机轮距计算排肥器最大倾角为2.39°，结合上述排肥量模型试验结果，开展满足常规水田施肥量、排肥器倾斜3°条件下的排肥量试验，试验结果如表6所示。由表6可知，排肥器倾斜时双行排肥量一致性变异系数相比水平时均有增加，转速为25 r/min、开度为15 mm时双行一致性变异系数最大，为6.17%，满足排肥质量要求。

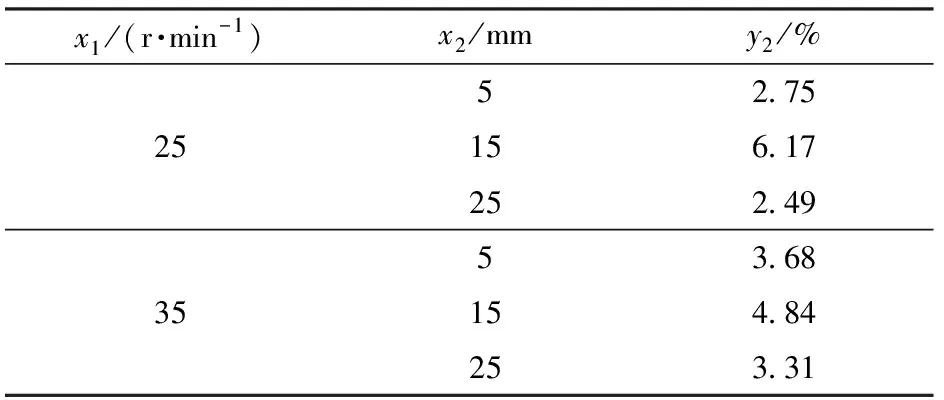
表6 排肥器倾斜状态下双行排肥量一致性变异系数试验结果

对总排肥量稳定性变异系数y3进行方差分析，结果表明圆锥转盘转速与排肥口开度对试验指标有显著影响(P<0.01)，曲线拟合得到转速和排肥口开度对总排肥量稳定性变异系数的回归方程为

y3=2.970 2+0.009 61x1-0.113 45x2+

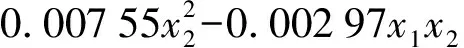
(17)

在试验范围内，基于Design-Expert 6.0.10软件中Optimization模块，获取总排肥量稳定性变异系数的最大值，即转速为15 r/min、排肥口开度为25 mm时，y3max为3.88%，与试验所得3.52%相差较小，满足文献[25]中总排肥量稳定性变异系数小于等于7.8%的要求。

对排肥均匀性变异系数y4进行方差分析，结果表明圆锥转盘转速与排肥口开度对试验指标有显著影响(P<0.01)，回归方程为

y4=25.773 67-0.513 41x1-0.857 42x2+

(18)

在试验范围内，当转速为15 r/min、排肥口开度为5 mm时，y4max为15.76%，与试验所得15.79%相差较小，满足文献[25]中排肥均匀性变异系数小于等于40%的要求。

5 结论

(1)针对黑龙江省寒地水田侧深施肥农艺要求，设计了一种圆锥盘推板式侧深施肥排肥器，对其工作原理进行阐述，建立了圆锥转盘单圈排肥量数学模型，分析确定了排肥器相关结构参数，通过运动学与力学模型建立得出圆锥转盘转速是影响排肥效果的关键因素，确定转速为15～45 r/min。

(2)通过离散元仿真技术探究推板数量对肥料填充特性与排肥性能的影响规律，结合理论分析确定推板数量为8时，具有最佳排肥性能。

(3)台架试验结果表明，排肥量与圆锥转盘转速和排肥口开度均具有良好的线性关系，与圆锥转盘转速相关性更强，排肥量范围在122～934 kg/hm2之间；圆锥转盘转速和排肥口开度对总排肥量稳定性变异系数与排肥均匀性变异系数有显著影响，对双行排肥量一致性变异系数影响不显著，变异系数最大值分别为3.81%、15.79%、3.88%，倾斜状态下双行排肥量一致性变异系数最大值为6.17%，满足水田侧深施肥排肥量与排肥性能要求。